前回「0からわかるPID制御」という記事を書きました.今回はPID制御の欠点に注目し,それを改良する方法について探りたいと思います.実装は後編で行うことを予定しています.
PID制御の欠点
以前用いた条件設定でPID制御の欠点を考えます.
PID制御の式は以下のように書くことができます.
steer = K_p cte + K_D \frac{d}{dt}cte + K_I \sum cte
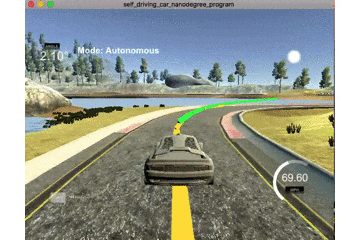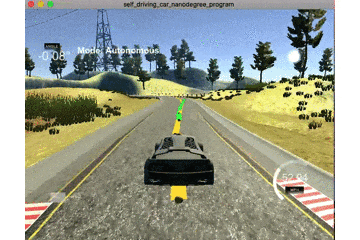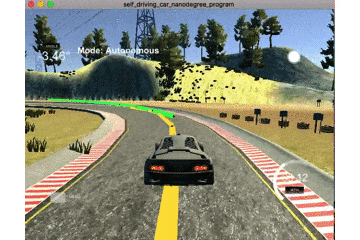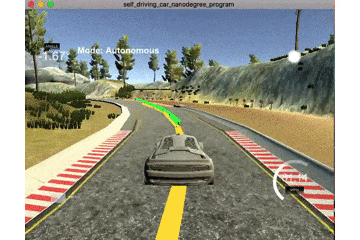
この式を見ると,現在と過去の情報しか用いることができていません.そのためコーナーに差し掛かったときは以下のgifのような挙動となります.

何が起こっているかというと,
・減速せずにコーナーに入る.
・CTEが大きくなる.
・CTEを小さくするために,急ハンドルを切る.
・急ハンドルを切ったために挙動がしばらく振動的になる.
また,別の欠点として,制御量を入力するまでの時間差を考慮することができないことも挙げられます.(0秒で目標のハンドル角に合わせることが不可能)
一方人間が自動車をコントロールする場合は次のようにします.
・コーナーを確認する.
・コーナーに入る前に減速する.
・減速後にハンドルを切り,目標軌道を進む.
・加速する.
人間が自動車を運転するように滑らかな軌道を描くためには,どのように制御すればいいのでしょうか?
そのような方法の1つに,あらかじめ軌道を予測し,その予測に対して操作量(ハンドル量とアクセル量)を入力するという方法が考えられます.この方法はモデル予測制御を用いることにより,実現することが可能です.今回はこの手法について検討したいと思います.
モデル予測制御とは
モデル予測制御とは「制御対象のモデルを利用し,最適制御問題を解くことにより,将来の予測値を求め,その予測値を用いて制御する方法」です.元々は,サンプリング周期の長い化学プラントや電力プラント等で用いられていましたが,近年の演算処理能力の工場により,サンプリング周期の短い対象についてもリアルタイムに予測することが可能となりました.そこで,今回は自動車シミュレータにモデル予測制御を適応しようと思います.
モデルの構築
モデル予測制御を利用するには,制御対象のモデルを構築する必要があります.そこで,自動車のモデルを構築します.正確なモデリングには,車体に加わる力を詳細に記述したDynamicモデルを用いる必要がありますが,今回は単純なKinematicモデルを用いることにします.
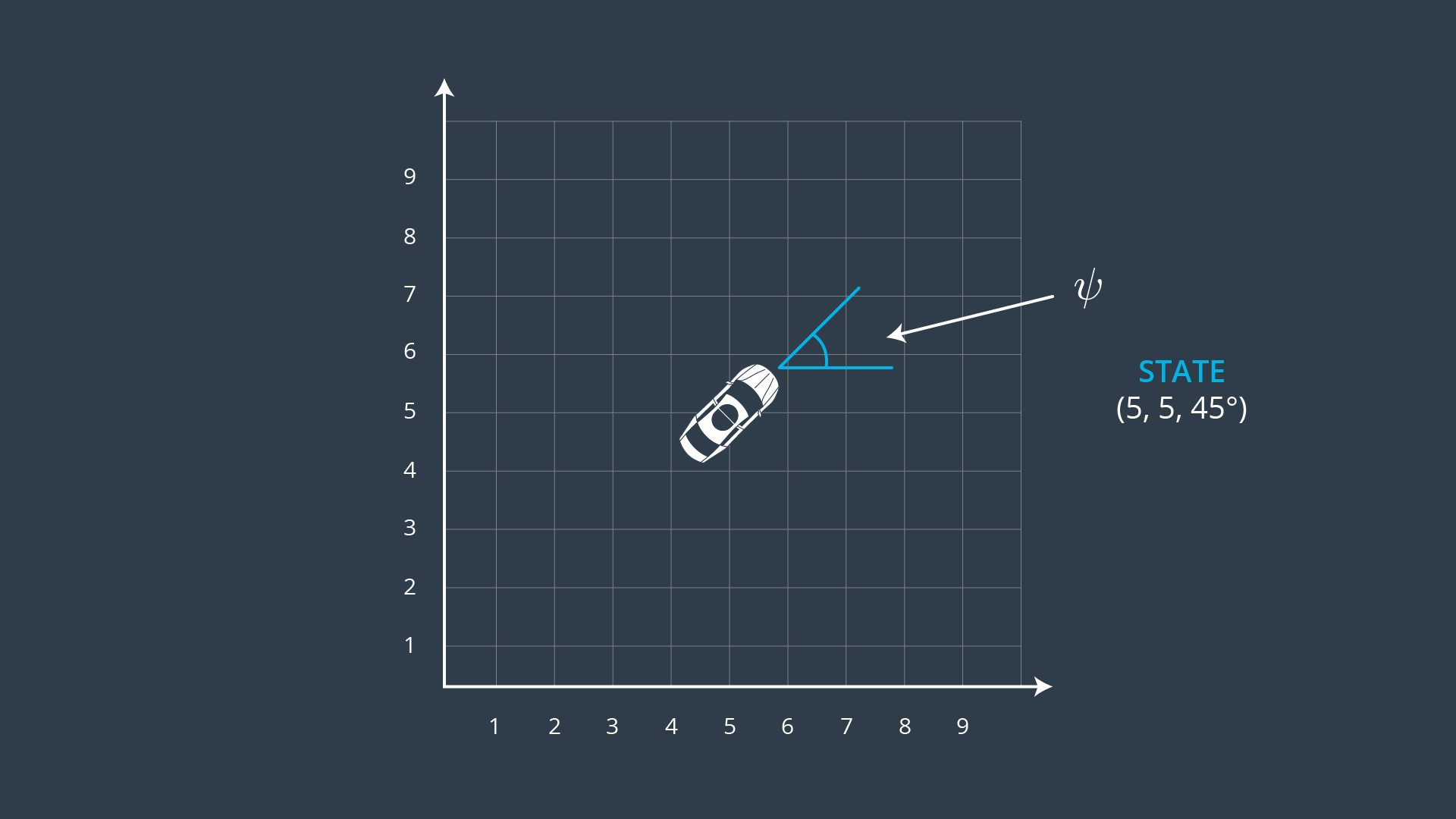
(quoted from Udacity's lecture)
自動車の位置と速度を$(x,y,\psi,v)$と表し,入力量を$(\delta,a)$とします.ただし$\delta$はハンドル角,$a$はアクセル量を表します.
自動車の状態について以下の式が導くことができます.
x_{t+1} = x_{t} + v_{t}\cos{\psi_{t}}dt \\
y_{t+1} = y_{t} + v_{t}\sin{\psi_{t}}dt \\
v_{t+1} = v_{t} + a_{t} dt \\
\psi_{t+1} = \psi_{t} + \frac{v_{t}}{L_f} \delta_{t}dt \\
ここで,$L_f$は自動車の先端から重心までの距離とします.
$\psi_{t+1} = \psi_{t} + \frac{v_{t}}{L_f} \delta_{t}dt$の式はこちらを参考にしました.
また,「0からわかるPID制御」での問題設定と同じように道路の中心と自動車の位置との距離差CTE(Cross Track Error)を導入します.今回は角度も導入したので,CTEの基準線と現在の自動車のなす角$e\psi$も導入します.
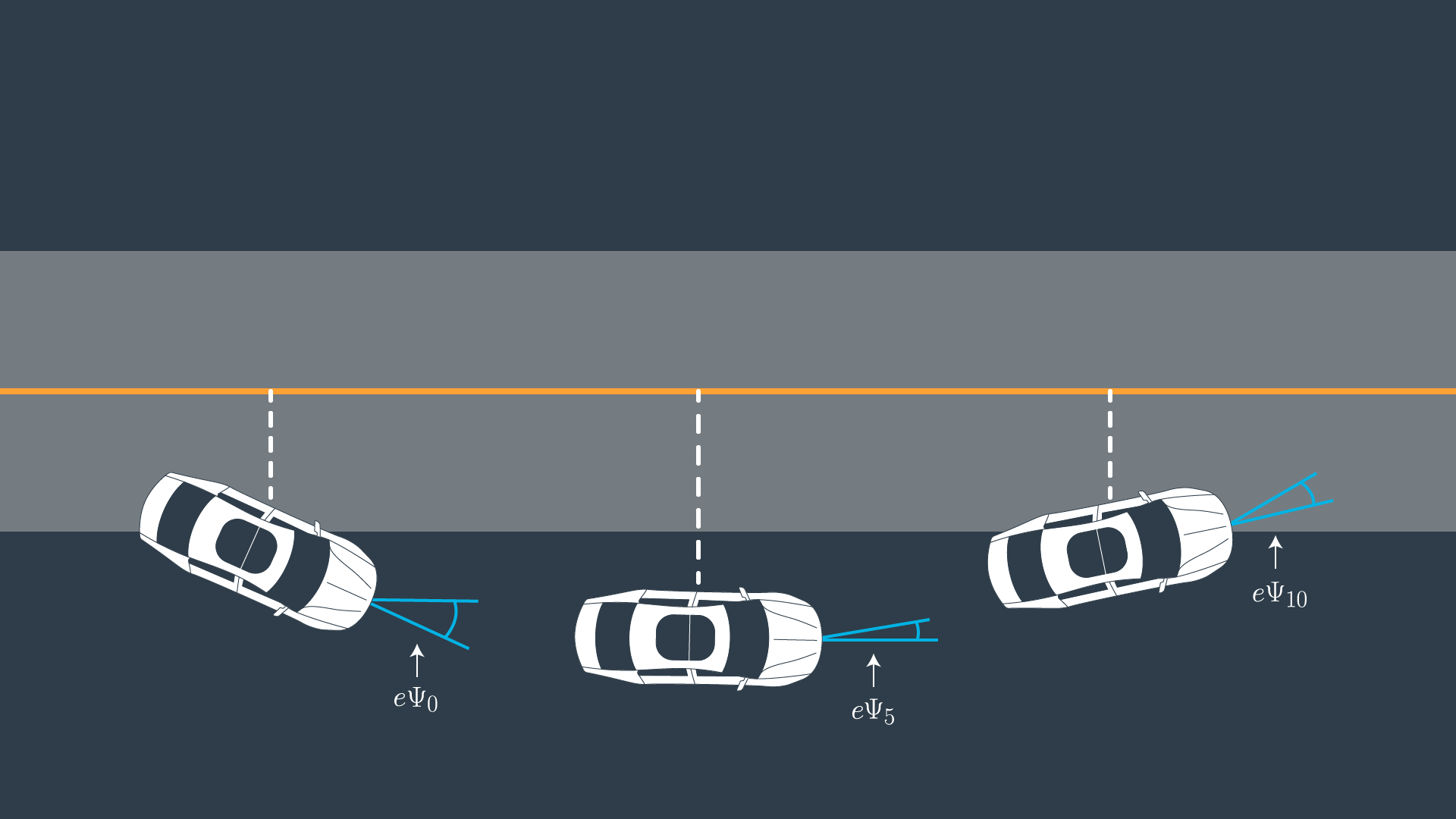
(quoted from Udacity's lecture)
cte_{t+1} = cte_{t} + v_t\sin{e\psi_t}dt \\
e\psi_{t+1} = e\psi_t + \frac{v_{t}}{L_f} \delta_{t}dt
と記述することができます.
最適制御問題とは
制御系の設計には,与えられた目標状態に達することだけが要求されることは少なく,その目標状態に達するまでの途中経過も設計仕様に与えられる場合が多くあります.今回のシミュレーターの例で言えば,「人間が自動車を運転しているような挙動を実現するために急ハンドル,急アクセル等を避けつつ,CTEを小さくすること」です.「人間が自動車を運転しているような」という条件の達成度をコスト関数で評価し,そのコスト関数を最小にする制御系を設計する問題のことを最適制御問題と言います.
最適制御問題を解くためには,コスト関数を設定する必要があります.そこでコスト関数として,必要なものとしては,以下のものが考えられます.
・CTE
・CTEの基準線と現在の車のなす角の角度差
以上のコスト関数のみの場合には,目標軌道に達したときには,コストが0となるため,自動車は移動する必要がなくなるため,自動車が静止してしまいます.
そのため,目標速度を決めて,コスト関数に含めるようにします.
また,人間が運転する軌道を再現しようとする場合には,急激なハンドル,アクセル量変化は望まれません.そのため,ハンドル,アクセル量の変化についてもコスト関数に含めるようにします.
すると以下のようなコスト関数ができます.
\int_0^T (a\times cte_{t}^2+b \times e\psi_t^2 +c \times (v_t-v_{ref})^2 + d \times (\delta_{t}-\delta_{t-1})^2 +e \times \delta_t^2 + f \times (a_{t}-a_{t-1})^2 + g \times a_t^2) dt
(ものすごい式になってしまいました...)
ここで,$v_{ref}$は目標速度,$a,b,c,d,e,f,g$は重みを表しており,自由に設定することが可能です.
例えば,CTEの重みに大きな値を入れるとCTEを素早く減少させるような操作入力が得られます.
また,それぞれのコストの単位が異なるため,重みは慎重に決定する必要があります.
この最適制御問題を解くためにはハミルトン・ヤコビ方程式と呼ばれる偏微分方程式を解く必要がありますが,理論が複雑なため割愛します.実装する際には,ある制限に対して偏微分方程式を解いてくれるライブラリーが存在しますので,それを用いて実装したいと思います.IPOPT(Interior Point OPTimizer)というライブラリーを使用します.
実装については次回行う予定です.
黄線が基準線で緑線が予測値となっています.
参考文献
最適制御問題については以下の本を参考にしました,
現代制御論