初めに
脳波の特徴量抽出に使われる手法としてFFTやウェーブレット変換などがありますが今回は空間のフィルタとしてCSP(Common Spatial Patterns)を紹介していきたいと思います。
この手法は脳波の運動想起に使われる手法ですが信号処理に使われている事例もあるためそこからの応用も可能かなと思います。
動画で見たい方はこちら
ドキュメントはこちら
と終わってしまってはこの記事の意味がないので、できる限るかみ砕いて書いていきたいと思います。
詳しく知りたい場合はこの2つを見ましょう。
脳波とは
前提条件として脳波取得は
このような機器を使用し脳波を取得します。この青色の電極ごとに脳波信号を取得することができます。この数が多ければ多いほど取得信号が多くなります。
このような機器から頭から出てくる脳波を取得し信号に変換することでコンピュータが数値として読むことが可能になります。
しかしながらここには問題があります。
1.ノイズが多い

abemaTVさんで載っている脳波計の種類です。大きく分けて2種類あります。
今回は見てわかる通り脳に直接電極を差し込んでいるわけではありません(怖い....)。なので、とてもノイズが多いです。
このノイズにより分類や検知に異常をきたしてしまいます。基本的には脳波の分類はこのノイズとの勝負です!!!
CSPはこのノイズを除去するために使われると思ってください。しかしながら、CSPはあるラベリングパターンで使われます。
2. ラベリングがしにくい
脳で思ったことが脳波に現れる。簡単に言うとこれが脳波なのですが思ったことというのがラベル付けは難しいです。
主に定常との差の問題です。何も考えていないということは人間にはありません。無意識化でも常に何かを考え、脳波が出ています。この定常と意識して考えた時の脳波の違いにラベルを付けるのですがこれが難しい。
タイミングの問題、本当に考ええているかの問題(被験者が解析者ではない場合)
なのでこれを解決するために3つの代表的な手法があります。
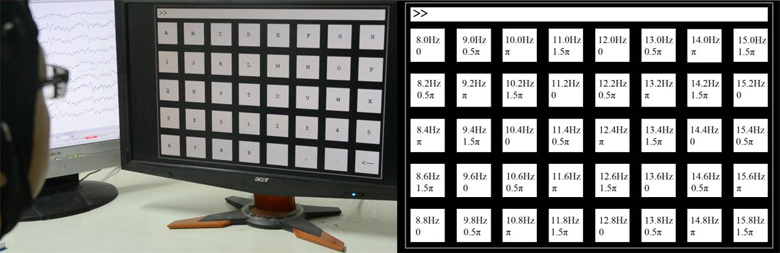
SSVEP
目に光を当てて脳波の定常状態を作り出し、そこから思い浮かべたことでラベル付け、分類する。(ただし自分的には対象者が思ったこととラベルが当たっているか、当たっていないかは悪魔の証明な気がする...)
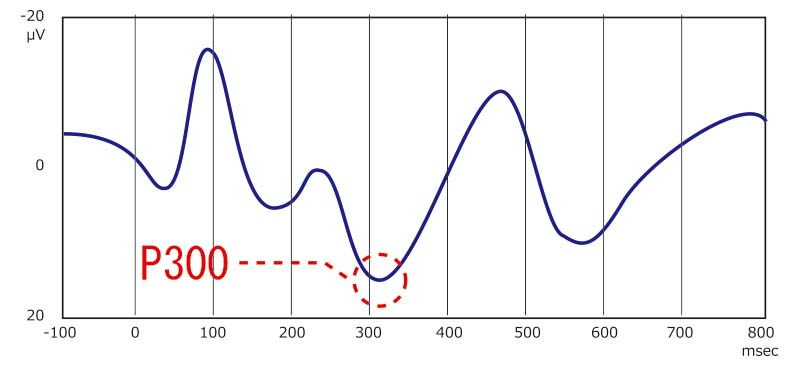
P300ベース
意思決定時の一定の時間で現れる脳波の事象をとらえる手法(ここら辺はまた長くなるので別記事で)
MIベース
体を動かすことを思い浮かべその動作からラベルつけする。(第三者が想起した脳波とラベルがあっているか見極めやすい)
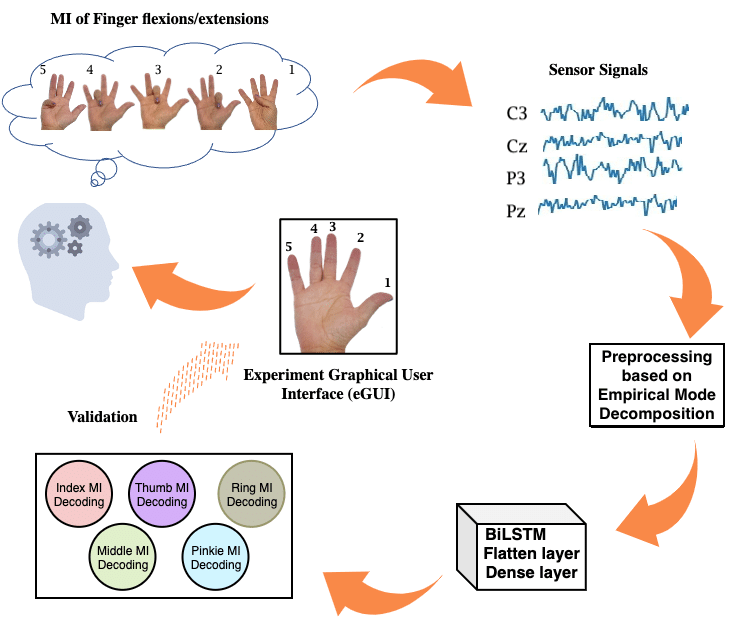
CSPはこのMIベース時に特徴量抽出とノイズ除去を行うため有効な手段と位置づけられています。
Common Spatial Patternsとはなにか?
Common Spatial Patternsとはなんぞや?このような疑問が生まれると思います。
これは2 つのクラス (条件) からの記録に基づいてマルチチャネル データを分析する手法です。
今回は数式はなしに話したいと思います。図や説明でなんとなくをつかんでください。
式や詳しい説明は上記の論文やまた書く別記事で....
さてCSPの説明です。
例えばですが2つのクラスを考えます。機械学習を用いて分類したい場合、このようにプロットされると理想です。
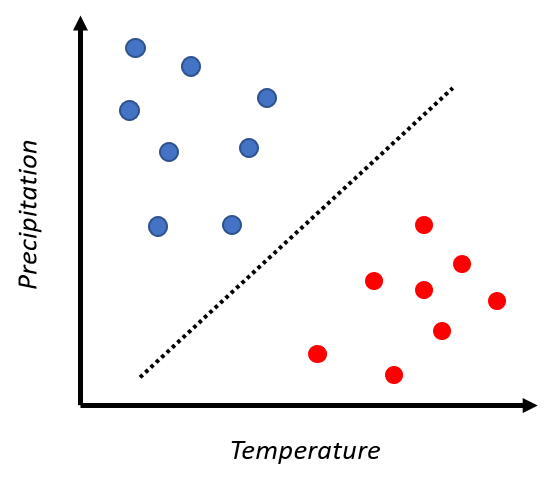
しかしながら、脳波はそううまくはいきません。
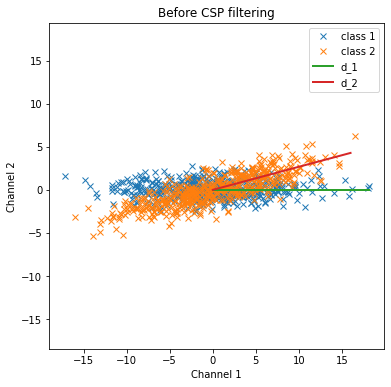
基本的にはこのようなプロットになってしまいます。
これではLDAなどの機械学習を使用しての分類は難しくなってしまいます。
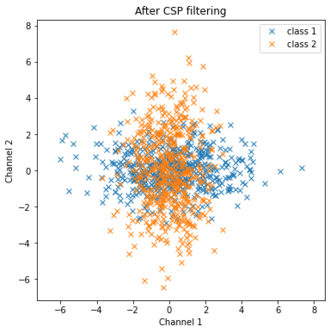
ここでCSPを使用します。
このようになることで機械学習でも識別がしやすい形になります。
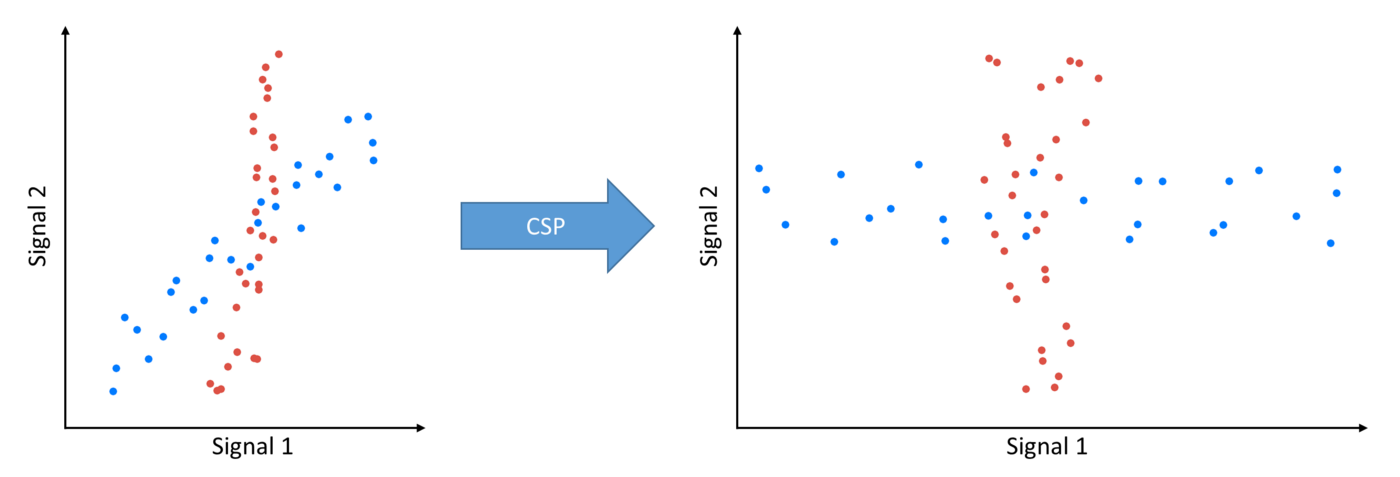
このように信号はもともと別々のクラスであったのがノイズにより似ているクラスになってしまいます。
このノイズを減らすのではなく違いをもっと出してやろうという手法がCSPです。
ここからの数式の引用は
ここからとってきていますのでより詳しく見たいかあはどうぞ..
自分なりの解説を入れながら説明していきます。間違えているところもあると思うのでそこはご指摘お願いします。
CSPの数式
脳波を取得するチャンネル数を m ,時間系列の最後の値を Nとすると
X=\left(
\begin{array}{ccc}
{\rm X_1}(0) & \ldots & {\rm X_1}(N)\\
{\rm X_2}(0) & \ldots & {\rm X_2}(N)\\
\vdots & \vdots & \vdots \\
{\rm X_m}(0) & \ldots & {\rm X_m}(N)
\end{array}
\right)
行列の行が脳波を取得する電極の信号だと思ってください。
例えば右手を動かすイメージを1、左手を動かすイメージを2とする。
わかりやすいように試行の回数は1にします。
そしてクラスごとの上記の脳波信号行列を
X_1 X_2
とします。
これらの数式の分散が最大になり,この分散比を特徴量を得ます。
なのでこれら2つの数式から共分散行列を取得します。
共分散とは二組の対応するデータの間の関係を表す数値です。
C_1 = \frac{X_1 X_i^T}{trace(X_1X_i^T)}\\
C_2 = \frac{X_2X_2^T}{trace(X_2X_2^T)}
このtraceは対角和です。線形台数で出される主対角成分の総和です。
2 つのタスクの合成分散共分散行列は
C = C_1 +C_2
また統計と確率は自分で別記事書きます。(自分のためのアウトプットです。)
共分散行列はこちらがわかりやすいです。
https://qiita.com/Seiji_Tanaka/items/5c8041dbd7da1510fbe9
共分散行列が分かると共分散行列に用いられている乱数の分布が分かる
これが魅力です。この乱数の分布を知りたいのです。
ここからCを固有値分解します。 理由としましては計算量削減と白色化行列を得るためです。
固有値分解はここをご参照ください。
白色化変換行列 Pと表現します
全体の共分散行列から白色化変換行列 Pを取得します
C = U_cλU_c^T \\
P = \sqrt{λ^{-1}U_c^T}
白色化は正規化に近い処理です。
numpy実装
これでそれぞれの共分散行列を白色化します。
S_1 = PC_1P^T \\
S_2 = PC_2P^T
ここで対角化行列をBを用いて分解すると
S_1 = Bλ_1B^T \\
S_2 = Bλ_2B^T
ここで共通の対角化行列Bができることがわかる。
ここからCSPの空間重み付けフィルターWは Pと B を用いて,
W = B^TP
となります。
この空間重み付けフィルターが重要な要素になってきます。
この空間重み付けフィルターはCNNが主流だと結構知られています。
ここから脳波信号Xにフィルターを通すと
Z = WX
2 タスク間で分散比に差が出やすいような信号Zが生成されます。
最後に,生成された信号 Z の最初の 1 行 Z_1 と最後の 1 行 Z_m を用いて,各チャンネルの特徴量を算出すると
f_1 = \log{\frac{var(Z_1)}{var(Z_1)+var(Z_m)}}\\
f_m = \log{\frac{var(Z_m)}{var(Z_1)+var(Z_m)}}\\
f = [f_1,f_m]
となる。
これがCSPの数式である!!!!
これを機械学習のモデルで学習させます。
最後に
脳波、難しい
やっぱり線形代数って大事だなーと思いました。
これからもアウトプットを大事にしてもっと記事を書いていきます。