LoginSignup
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@RubyLrving(ruby lrving)

AtCoder Beginner Contest 418

Posted at

A - I'm a teapot

問題文

文字列の最後の3文字がteaか判定する問題です。
substringを使用しましょう。

C++
#include <bits/stdc++.h>
 
#define rep(i,n) for(int i=0; i<(n); ++i)
#define repx(i,x,n) for(int i=x; i<(n); ++i)
#define fixed_setprecision(n) fixed << setprecision((n))
#define execution_time(ti) printf("Execution Time: %.4lf sec\n", 1.0 * (clock() - ti) / CLOCKS_PER_SEC);
#define pai 3.1415926535897932384
#define NUM_MAX 2e18
#define NUM_MIN -1e9
 
using namespace std;
using ll = long long;
using P = pair<int,int>;
template<class T> inline bool chmax(T& a, T b){ if(a<b){ a=b; return 1; } return 0; }
template<class T> inline bool chmin(T& a, T b){ if(a>b){ a=b; return 1; } return 0; }

int main() {
    int n;
    cin >> n;
    string s;
    cin >> s;

    if(s.length() > 2 && s.substr(n-3, 3) == "tea"){
        cout << "Yes" << endl;
    }else{
        cout << "No" << endl;
    }

    return 0;
}

B - You're a teapot

問題文

問題文を理解するのが難しい問題です。
n <= 100の制約により、3重ループの全探索を行いましょう。

2点間を決める2重ループ。
tを求める3重目のループ。
と分けて考えると実装しやすいです。

C++
#include <bits/stdc++.h>
 
#define rep(i,n) for(int i=0; i<(n); ++i)
#define repx(i,x,n) for(int i=x; i<(n); ++i)
#define fixed_setprecision(n) fixed << setprecision((n))
#define execution_time(ti) printf("Execution Time: %.4lf sec\n", 1.0 * (clock() - ti) / CLOCKS_PER_SEC);
#define pai 3.1415926535897932384
#define NUM_MAX 2e18
#define NUM_MIN -1e9
 
using namespace std;
using ll = long long;
using P = pair<int,int>;
template<class T> inline bool chmax(T& a, T b){ if(a<b){ a=b; return 1; } return 0; }
template<class T> inline bool chmin(T& a, T b){ if(a>b){ a=b; return 1; } return 0; }

int main() {
    string s;
    cin >> s;
    int n = s.length();
    
    double ans = 0;
    rep(i, n){
        rep(j, n){
            if(s[i] == 't' && s[j] == 't'){
                int cnt = 0;
                for(int k = i; k <= j; k++){
                    if(s[k] == 't') cnt++;
                }
                if(j - (i - 1) >= 3){
                    ans = max(ans, ((double)cnt - 2.0) / ((double)abs(j - (i - 1)) - 2.0));
                }
            }
        }
    }
    cout << fixed_setprecision(10) << ans << endl;
    return 0;
}

C - Flush

問題文

累積和の問題です。
私はコンテスト中の考察が足らなくて累積和、二分探索で解きました。
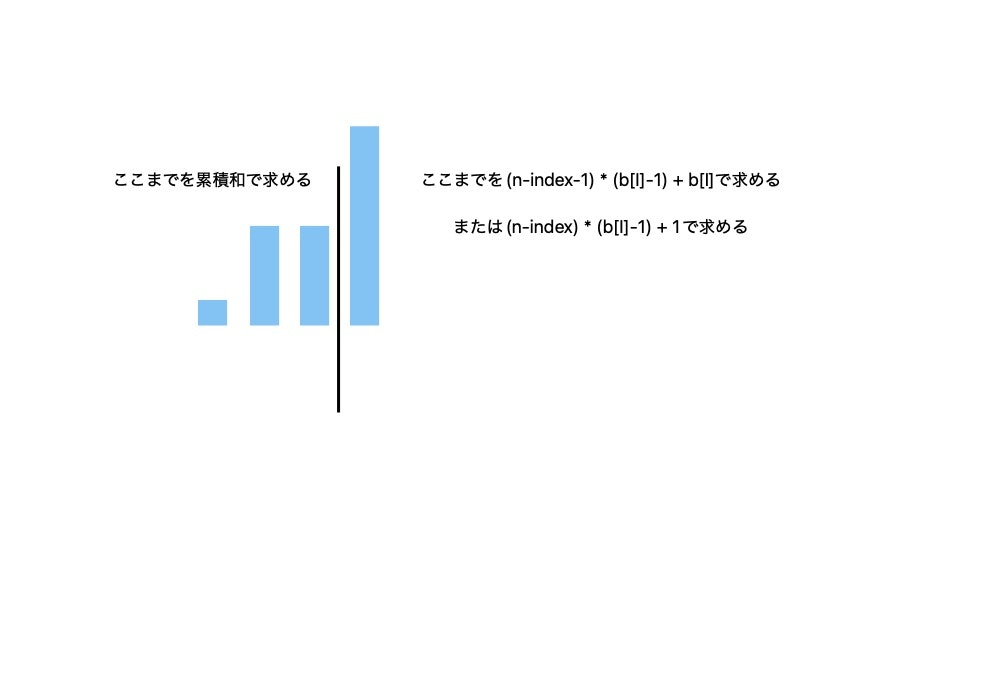
サンプル１の入力で考察します。

シーン1のコピー.jpg

図で書くとこのような形になります。
nとqで2重ループにするとTLEになります。
O((N+Q)logN)のイメージで解きました。

C++
#include <bits/stdc++.h>
 
#define rep(i,n) for(int i=0; i<(n); ++i)
#define repx(i,x,n) for(int i=x; i<(n); ++i)
#define fixed_setprecision(n) fixed << setprecision((n))
#define execution_time(ti) printf("Execution Time: %.4lf sec\n", 1.0 * (clock() - ti) / CLOCKS_PER_SEC);
#define pai 3.1415926535897932384
#define NUM_MAX 2e18
#define NUM_MIN -1e9
 
using namespace std;
using ll = long long;
using P = pair<int,int>;
template<class T> inline bool chmax(T& a, T b){ if(a<b){ a=b; return 1; } return 0; }
template<class T> inline bool chmin(T& a, T b){ if(a>b){ a=b; return 1; } return 0; }

int main() {
    ll n, q;
    cin >> n >> q;
    vector<ll> a(n), aa(n+1);
    rep(i, n) cin >> a[i];
    vector<ll> b(q);
    rep(i, q) cin >> b[i];
    sort(a.begin(), a.end());
    rep(i, n) aa[i+1] = aa[i] + a[i];

    rep(i, q){
        if(b[i] == 1){
            cout << 1 << endl;
            continue;
        }

        int index = lower_bound(a.begin(), a.end(), b[i]) - a.begin();
        if(index < n){
            cout << aa[index] + (n - index - 1) * (b[i] - 1) + b[i] << endl;
        }else{
            cout << -1 << endl;
        }
    }

    return 0;
}

O(N+Q)
こちらが正攻法の回答になります。
すぬけさんのコードは綺麗だな。

C++
#include <bits/stdc++.h>
 
#define rep(i,n) for(int i=0; i<(n); ++i)
#define repx(i,x,n) for(int i=x; i<(n); ++i)
#define fixed_setprecision(n) fixed << setprecision((n))
#define execution_time(ti) printf("Execution Time: %.4lf sec\n", 1.0 * (clock() - ti) / CLOCKS_PER_SEC);
#define pai 3.1415926535897932384
#define NUM_MAX 2e18
#define NUM_MIN -1e9
 
using namespace std;
using ll = long long;
using P = pair<int,int>;
template<class T> inline bool chmax(T& a, T b){ if(a<b){ a=b; return 1; } return 0; }
template<class T> inline bool chmin(T& a, T b){ if(a>b){ a=b; return 1; } return 0; }

int main() {
    ll n, q;
    cin >> n >> q;
    vector<ll> a(n), aa(1000000+1), bb(1000000+1);
    rep(i, n) cin >> a[i];
    vector<ll> b(q);
    rep(i, q) cin >> b[i];
    sort(a.begin(), a.end());
    rep(i, n) aa[a[i]] += a[i];
    rep(i, n) bb[a[i]]++;
    rep(i, 1000000){
        aa[i+1] = aa[i+1] + aa[i];
        bb[i+1] = bb[i+1] + bb[i];
    }

    rep(i, q){
        if(b[i] == 1){
            cout << 1 << endl;
            continue;
        }

        ll ans = aa[b[i]-1] + (n - bb[b[i]-1]) * (b[i]-1) + 1;
        if(bb[b[i]-1] == n){
            cout << -1 << endl;
        }else{
            cout << ans << endl;
        }
    }

    return 0;
}

D - XNOR Operation

問題文

dpの問題です。
漸化式は、

C++
    rep(i, n){
        if(t[i] == '0'){
            dp[i+1][0] = dp[i][1] + 1;
            dp[i+1][1] = dp[i][0];
        }else{
            dp[i+1][0] = dp[i][0];
            dp[i+1][1] = dp[i][1] + 1;            
        }
        ans += dp[i+1][1];
    }

Sに残った唯一の文字を1にすることができるか、
という問題なので

C++
ans += dp[i+1][1];

で取り出しています。

C++
#include <bits/stdc++.h>
 
#define rep(i,n) for(int i=0; i<(n); ++i)
#define repx(i,x,n) for(int i=x; i<(n); ++i)
#define fixed_setprecision(n) fixed << setprecision((n))
#define execution_time(ti) printf("Execution Time: %.4lf sec\n", 1.0 * (clock() - ti) / CLOCKS_PER_SEC);
#define pai 3.1415926535897932384
#define NUM_MAX 2e18
#define NUM_MIN -1e9
 
using namespace std;
using ll = long long;
using P = pair<int,int>;
template<class T> inline bool chmax(T& a, T b){ if(a<b){ a=b; return 1; } return 0; }
template<class T> inline bool chmin(T& a, T b){ if(a>b){ a=b; return 1; } return 0; }

int main() {
    ll n;
    cin >> n;
    string t;
    cin >> t;
    ll ans = 0;
    vector<vector<ll>> dp(n+1, vector<ll>(2, 0));
    rep(i, n){
        if(t[i] == '0'){
            dp[i+1][0] = dp[i][1] + 1;
            dp[i+1][1] = dp[i][0];
        }else{
            dp[i+1][0] = dp[i][0];
            dp[i+1][1] = dp[i][1] + 1;            
        }
        ans += dp[i+1][1];
    }
    cout << ans << endl;

    return 0;
}
1
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?