前説
この記事では、普段はエンジニアとして仕事をしている私が、あまりこれまで気にしてこなかったパソコンってどういう仕組みなのでしょうか？という疑問に答えるために自習をした記事です。
読みづらい部分等がありましたら申し訳ございません。
参考サイト
http://startelc.com/elc/elc1_nElc.html
http://www.kairo-nyumon.com/analog_guide.html
https://sagara-works.jp/research-and-development/transistor/
ゴール
CPUを自作してみたい！
コンテンツ
基礎編
- 第1章 アナログ回路について
- アナログ回路はなぜ難しい？
- アナログ回路の設計に必要な基礎知識
- 第2章 電気回路 入門
- 電気回路の基礎
- 容量とインダクタ
- 交流回路と複素数
- インピーダンスとアドミタンス
- 交流回路（交流理論）の基礎
- 電気回路のまとめ
- 第3章 制御工学 入門
- 制御工学（制御理論）の基礎
- ラプラス変換
- 制御工学の問題の解き方
- 伝達関数の求め方
- 伝達関数ってなに？
- 周波数特性とボード線図
- フィードバック制御
- 第4章 アナログ電子回路
- アナログ電子回路の基礎
- トランジスタの特性
- 増幅回路の動作原理
- 負荷線の引き方
- バイアス電圧と信号電圧
- 周波数特性の考え方
- フィードバック（負帰還）
- 第5章 オペアンプ
- オペアンプとは何か？
- オペアンプの特徴
- オペアンプがすごい理由
実践編
- 第1章 実践で習得！電子回路
- 工作で覚える電子回路
- 当サイトに沿って学習する方法
- 必要な工具・測定器
- 電子部品などの揃え方
- 格安オシロスコープ
- 「はんだ」を使わない電子工作
- 第2章 初心者に最適 学習キット
- キットで遊ぼう電子回路
- 学習キット組み立ての様子
- 第3章 矩形波 発生回路
- 矩形波（方形波）を作る
- 抵抗分圧回路
- コンパレータ（比較器）
- 矩形波（方形波）発生回路
- RC回路と時定数
- 矩形波（方形波）発生回路の理論的な理解
- 第4章 明るさ調整 LED回路
- LED回路を作る
- PWM信号を作る
- PWM信号を使ったLED回路
- 反転増幅回路を作る
- 非反転増幅回路を作る
- 第5章 三角波 発生回路
- 三角波を作る
- 積分回路
- 三角波発生回路を作る
これまでの軌跡
1章(アナログ回路について)：https://qiita.com/Rowing0914/items/adbc89bdfb27596e065d
前回を振り返ると、アナログ回路をここから説明していきますよ、という内容であったと思います。
それにあたって三つの必要な理論を理解しないといけなく、それをここからの章で説明をしていく流れが前回の章の説明ですね。
では始めます。
電気回路(回路理論)とは？
電気回路で扱う内容は、大きく分けると「直流回路（DC）」と「交流回路（AC）」になります。直流回路および交流回路といった電気回路の解析方法をまとめたものが回路理論です。
この分野には大きく分けて二つの回路のクラスがあります、それは先ほどの電流の部分で見たように、
- 直流回路：DC => オームの法則、抵抗やコンダクタンス(電気の流れやすさの概念)
- 交流回路：AC => 複素数、サイン波に対する解析
と言ったキーワードを中心に学習を進めていきます。
直流回路と基礎
オームの法則見ていきます。
この法則は抵抗という素子の両端にかかる電圧を V 、そのとき抵抗に流れる電流を I とすると式(1) のように求まります。
V = G \times V \tag{1}
また、抵抗という概念を導入したいと思います。
抵抗とは電気の流れに対して抵抗となる素子のことを意味します。つまり、抵抗(Resistance)を示す$R$は電流を妨げる度合いを表します。そして、ここでコンダクタンス(電流の流れやすさの度合い)も取れいれてみると下記の式になります。
G = \frac{1}{R} \\
I = G \times V \tag{2}
つまり、抵抗値が「電流の流れを妨げる度合い」であれば、コンダクタンスの値は「電流が流れやすい度合い」ということになります。
交流回路の基礎
交流回路では角速度（または角周波数ともいう） ω 、振幅 A の正弦波交流（サイン波）の入力 A×sin(ωt) に対して、出力がどのようになるのかを解析します。 t は時間を表します。交流回路で扱う素子は抵抗に加えて、容量（コンデンサ）やインダクタ（コイル）といった素子が登場します。
これについて説明を加える前に新しい概念である、角速度と正弦波交流とは何なのかを見てみたいと思います。
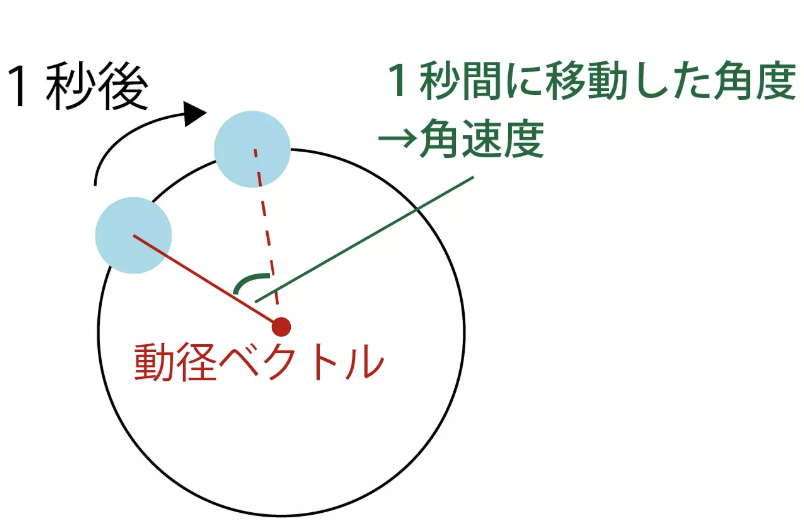
角速度とは ~概念の説明~
円の中心から物体に向けて引いた線のことを動径ベクトルといい、動径ベクトルが１秒間に回転する角度（回転角）のことを角速度と言います。
参考サイト
角速度とは ~公式をみてみる~
前述したように、角速度は、物体が１秒間で何°回転したか（動いたか）でしたね。
さて、下のイラストのように、円周に沿って一定の速さで動く物体の動径ベクトルがt[s]間にθ[rad]回転した（動いた）とします。
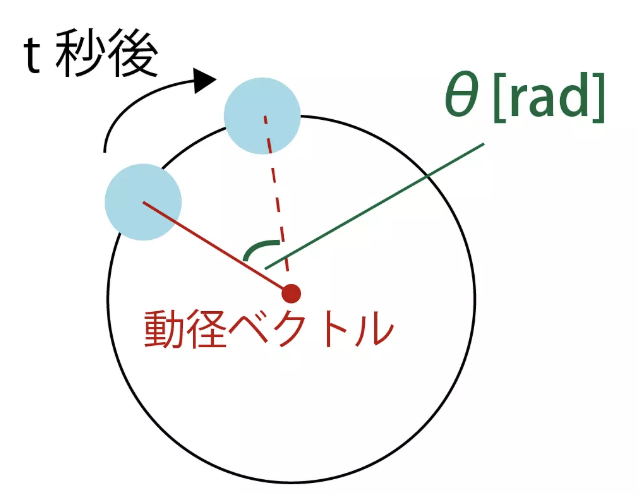
これをもとに角速度$w$を計算してみると、
$\frac{動いた量}{動いた時間}$ で良いので、
$w = \frac{\theta}{t} [rad/s]$ となります。
もう少し深い関係を見てみましょう、。
角速度と円周や半径との関係
物体が円周上をT(周期と呼び、単位はs)秒かけて１周するとします。円の半径をr[m]、物体の速度をv[m/s]とします。
すると、物体は周期T[s]の間に円周上2πr[m]移動することになるので
$v = \frac{動いた距離}{かかった時間} = \frac{2πr(円周)}{T(かかった時間)}$
$T = \frac{2πr}{v}$
と表せます。
そして、実際に動いた角度としては、一周は2πであるので、それを$\theta$に代入すると、
$w = \frac{\theta}{T} = \frac{2π}{T} = \frac{2πv}{2πr} = \frac{v}{r}$
となります。これが半径と角速度の関係を表す重要な公式となるのです。
正弦波交流とは
こちらに飛び込む前に、正弦波を理解しないといけませんね。
では、まずそちらからみてみましょう。
正弦波とは
実は正弦波(sin波)というものの理解には高校物理で習った単振動という概念が欠かせません。
そちらを確認した上で、それがどういう風に正弦波に関わっているのかをみていきましょう。
ちなみに、今回参照するサイトはこちらです。
http://wakariyasui.sakura.ne.jp/p/wave/hadou/seigennha.html
波をよく伝える媒質はばねの性質を持ちます。ばねの性質が無いものは波をよく伝えることができません。ばねは、伸ばされれば伸ばされるほど強い力で引き戻そうとします。この力を復元力といいますが、復元力を持つものは単振動という動きをします。次にこれを先ほどの角速度で見たように、円周上を等速に回転する物体を使ってイメージしてみましょう。
物体が円周上を一定の速さでまわり続ける運動を等速円運動と呼びますが、この物体に横から光を当てると壁に映った影は周期的な往復運動をし、この運動を単振動と呼びます。
そして、この単振動の軌道を時間とその時の位置関係をグラフに落とし込んだものが正弦波と呼ばれるものとなるのです。
アニメーション等を使っていただいた素晴らしいグラフがありますので、先ほどの参照サイトをご覧ください！
そして、ここから正弦波の式を確認してみましょう。
正弦波の公式
正弦波においては各点は単振動の動きをしますので、たとえばy軸上におけるの物体の変位(この場合は高さを表す)を振幅($A$ : amplitude)と角速度($w$)を用いて表現をすると下記の洋梨気になります。
$y = A \sin(wt)$
**物体が運動して位置が変わったとき、その位置の変化量を変位といいます。
参照先：http://wakariyasui.sakura.ne.jp/p/mech/henni/henni.html
正弦波交流とは、に立ち戻る
参照先：https://www.yonago-k.ac.jp/denki/lab/nitta/lecture/E2_e-circuit1/note/note11.pdf
これまでみてきたことを振り返ると、正弦波交流とは、要は正弦波の周期に従った交流的な変化を許容するものということですね。
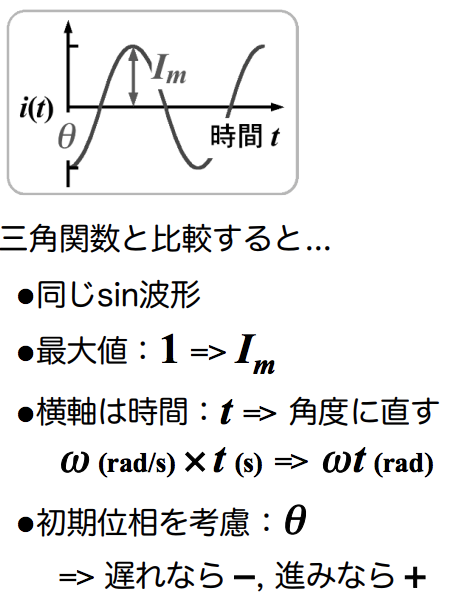
ここで正弦波交流の式を構成する要素を一つずつ見ていきましょう。
公式： $ i(t) = I_m \sin(wt ± \theta ) $
- 角速度：単位時間に動く角度のこと$w$単位は(rad)
- 振幅：波形の大きさを表す$A$
- 周波数：波形の繰り返し頻度を表す $f = \frac{1}{周期 T(s)}$であり単位は$Hz$
- 位相：波形の時間的なズレを表す角度$\theta$
- 瞬時値(正弦波交流の公式)：$i(t)$ => 波形の時間的な変化を表す
となります。
ここで周波数をもとに再度、角速度と位相の関係を見直してみましょう。
ここで二つ例を考えて見ましょう。
1秒間あたりに1回転をしたとしましょう。すると、角速度は
f = 1 Hz\\
w = 2π => (\frac{rad}{s})
となりますね。
もし1秒間あたりに2回転をしたとしましょう。すると、角速度は
f = 2 Hz\\
w = 4π => (\frac{rad}{s})
よってこの関係より、周波数と角速度は下のような関係であると確認できます。
w = 2πf
また、正弦波において今回確認したのは、角度であり、実際の波の大きさを決める振幅を値として組み込んだものを考えますと下記の図のように考えられます。
よって、
。。。前置きが長くなってしまいまして申し訳ございません、、ここからやっと交流回路の本題へと戻れます。。。
さて、角速度と正弦波交流を理解できたところで、前述の交流回路で用いる回路記号は以下の図1 のように表されます。
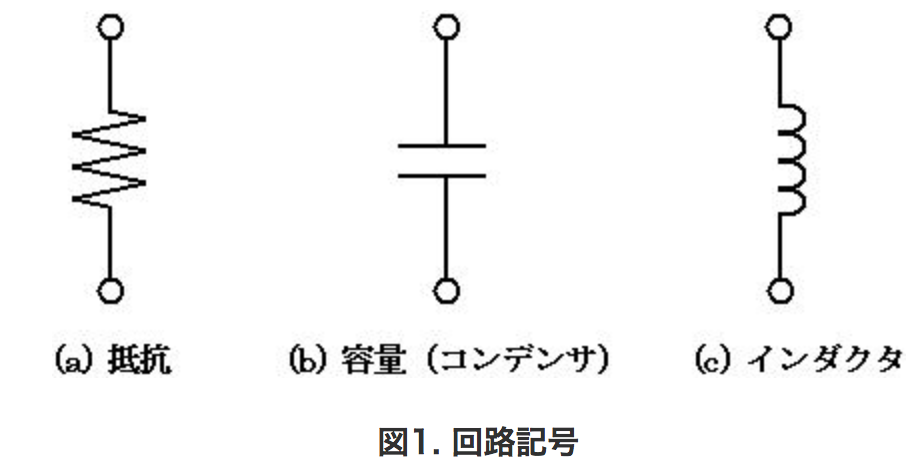
これらの素子で構成された回路は、正弦波交流の入力 A×sin(ωt) に対して振幅と位相のみが変化するというのが特徴です。つまり交流回路は、図2 の上図のような入力に対して、出力の振幅の変化と位相のずれのみが分かれば入力と出力の関係が分かるということになります（図2 の下図）。
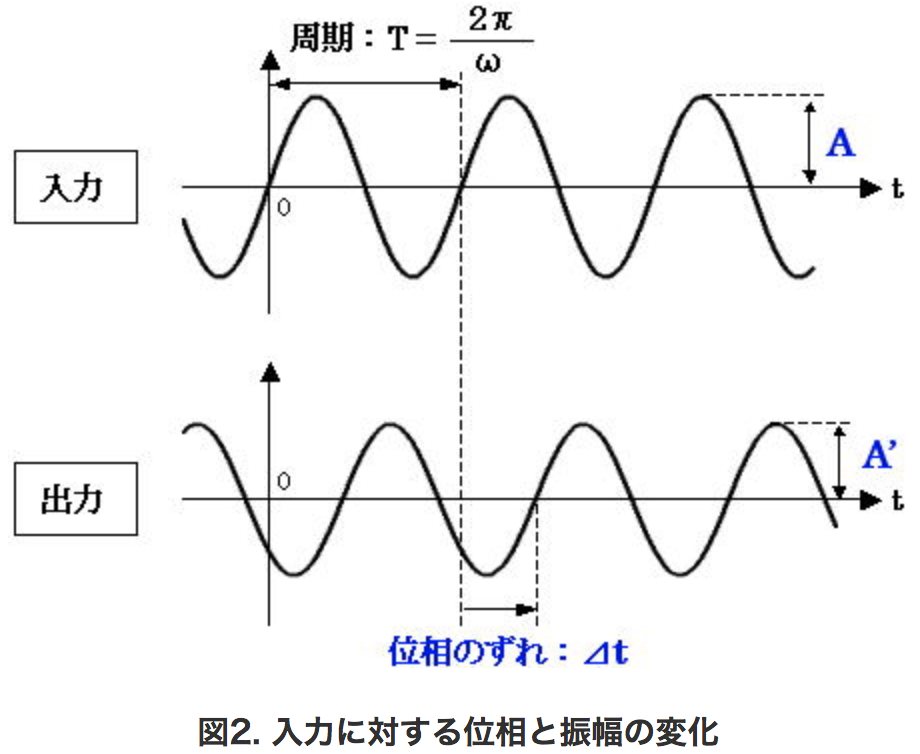
交流回路の計算では複素数を用いて振幅と位相の変化量を求めます。この複素数を用いることによって交流回路の計算は非常に簡単なものになるのです。
それでは次に、抵抗とコンダクタンスを使った直流回路の計算について説明します。抵抗とコンダクタンスを使った計算は交流回路の計算の基礎にもなるもので
直流回路の計算
まずは、下図にあるような二つの直流回路の組み方を元のそこで各箇所に設置をされた抵抗がどの程度効いてくるのかを確認してみましょう。
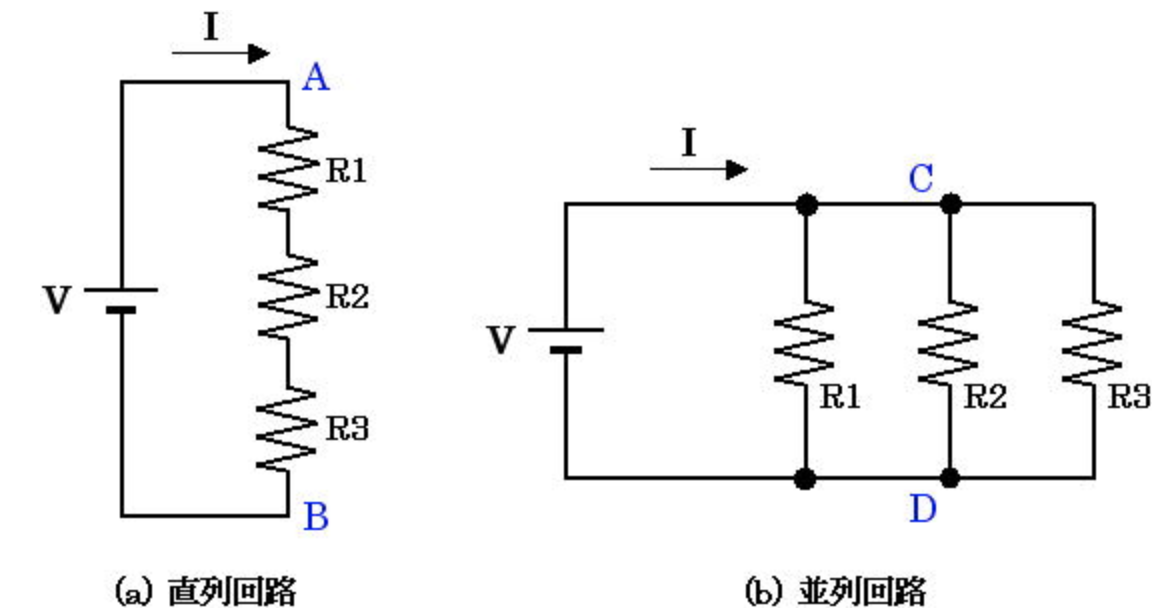
ここで合成抵抗$R_{total}$を求めてみたいと思います。
Case (a)\\
R_{total} = R_1 + R_2 + R_3\\
I = \frac{V}{R_{total}} = \frac{V}{R_1 + R_2 + R_3}\\
Case(b)\\
\frac{1}{R_{total}} = \frac{1}{R_1 + R_2 + R_3}\\
I = \frac{V}{R_{total}} = (\frac{1}{R_1 + R_2 + R_3}) \times V\\
** 並列に接続された抵抗の合成抵抗についてですが、各抵抗の逆数の和が、合成抵抗の逆数となります。
回路理論における直流回路の計算
回路理論では、電気回路をパズルのように計算をしていきますが、いくつかの決まりごとを定めております。
その決まりごとを見る前に、一章でできたコンダクタンス(電流の流れやすさ)の計算方法を見ておきましょう。至極簡単で抵抗の逆数です。$G = \frac{1}{R}$
ですので、先ほどの並列回路の抵抗の計算なども、下記のように簡略化できます。
$G_{total} = G_1 + G_2 + G_3$
では、抵抗とコンダクタンスの使い分けに関する決まりごとを観て参りましょう、
- 求めるものが電流過電圧化により抵抗かコンダクタンス化の使い分けをする。
- 電圧： $V = R_{total} \times I$
- 電流： $I = G_{total} \times V$
- 並列回路か直列回路かで使い分けをする。
- 直列回路：$R_{total} = R_1 + R_2 + R_3$
- 並列回路：$G_{total} = G_1 + G_2 + G_3$
さて、これまで見てきた知識をもとに次の新しい領域へと進んでみましょう。
容量とインダクタ
このセクションでは、交流回路で用いられる容量（コンデンサ）とインダクタ（コイル）の特徴について説明します。容量やインダクタは、正弦波交流（サイン波）の入力に対して位相が 90度進んだり遅れたりするのが特徴です。ちなみに電気回路では抵抗も使われますが、抵抗は正弦波交流の入力に対して位相の変化はありません。
コンデンサ(容量)
参照先：https://www.murata.com/ja-jp/campaign/ads/japan/elekids/compo/capacitor
まずは、コンデンサの概要とその代表的な役割をみてみたいと思います。
コンデンサの基本は、空気や絶縁体をはさんで向かい合った2枚の金属板。そこに電圧をかけると、金属板に
電流が流れ込みます。
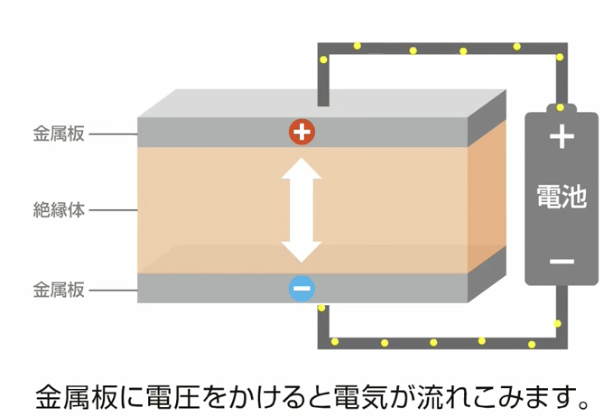
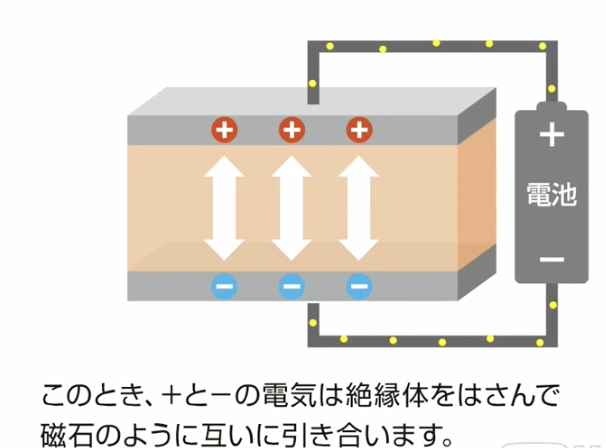そして、金属板に電荷がいっぱいにたまるとこれ以上は流れ込まなくなります。また、これ以上電圧をかけるのをやめても、絶縁体を挟んで互いの電極が異なるの引っ張り合い続ける形となります。また、ここで蓄積できる量を静電容量と呼びます。また、誘電率(電気を蓄えるのを助ける役割)が高い絶縁体を挟むことにより、静電容量を増やすことが可能です。そのような材料を誘電体と呼びます。以上簡単ながら概要の説明です。
さて、ここから要約した役割をいくつかみてみましょう。
- 電圧を安定させる
- ノイズを除去する
- 信号を取り出す
これらの説明に関しては詳しくはこちらをご覧ください。
https://www.murata.com/ja-jp/products/emiconfun/capacitor/2011/01/14/en-20110114-p1
コンデンサを簡単に理解したところで本題に戻ります、以降適宜容量をコンデンサと読み替えてください。
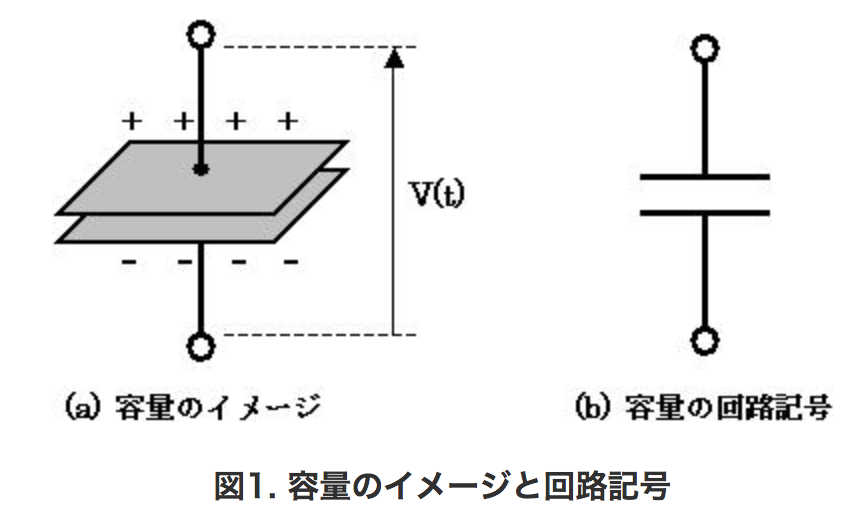
Q は電荷量、 C は容量値、 V は電圧です。Q(t) や V(t) の (t) は時間 t の関数であることを表し、電荷量と電圧は時間的に変化します。これを加味して、コンデンサを表す式を構成すると、
$Q(t) = C \times V(t)$
となります。
インダクタ(コイル)
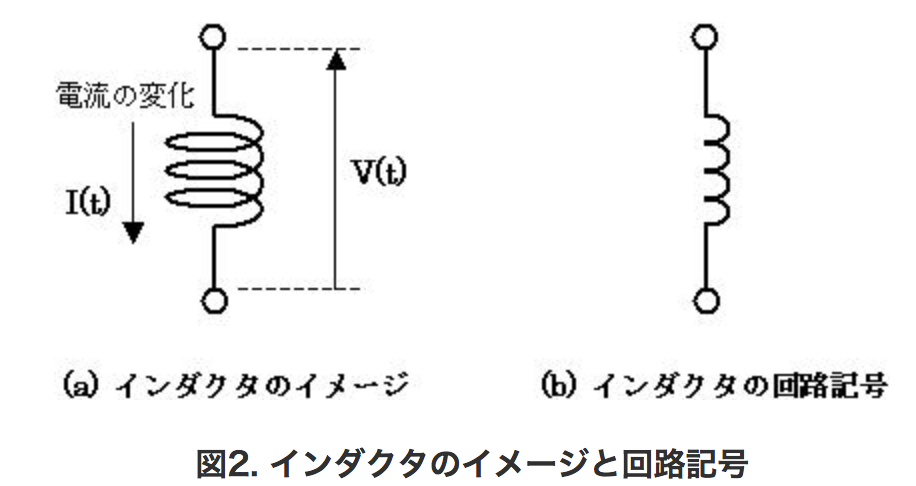インダクタは、電流の時間的な変化量（電流を時間で微分した値）に比例して、逆起電力が発生するという特徴を持ちます。 L はインダクタンスと呼ばれる定数であることを加味して、下記のようにインダクタを定式化できます。
$V(t) = L \frac{\partial I(t)}{\partial t}$