AtCoderログ：0040 - ABC 211 C

問題

問題文

文字列 $S$ が与えられます。このうち $8$ 文字を選び下線を引き、下線を引いた文字が左から順に c , h , o , k , u , d , a , i となるようにする方法は何通りありますか？
ただし答えは非常に大きくなる可能性があるので、$(10^9+7)$ で割った余りを出力してください。

制約

・$8 \le |S| \le 10^5$
・$S$ は英小文字からなる

回答

回答1 (AC)

問題文を読んだだけではルールがすぐにはわからないので、小規模な例を実際に試してルールを見つけるのがセオリーでしょう。

例として s="chcho" という文字列から下線部が "cho" になる場合を探してみます。いきなり 3 文字を探すのは難しいので、まず "c" を、次に "ch" を、最後に "cho" を探すことにします。

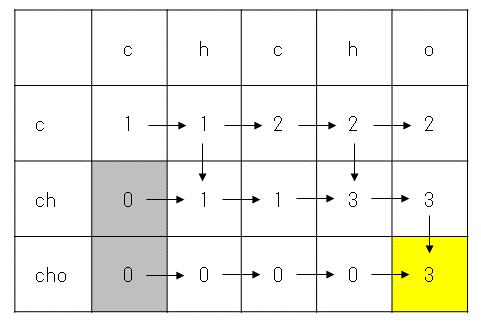
まず s から "c" を探すために s を一文字ずつチェックしていきます (下図の上から 2 行目)。s の 1 文字目は "c" なので、ここまでで見つかった c は 1 通りであり、表の上から 2 行目・左から 2 列目に 1 をかきます。s の 2 文字目は "h" なので、2 文字目までに見つかった "c" は 1 通りのままであり、表の上から 2 行目・左から 3 列目に 1 をかきます。s の 3 文字目は "c" なので、3 文字目までに見つかった "c" は 2 通りで、表の上から 2 行目・左から 4 列目に 2 をかきます。同様にして上から 2 行目・左から 5 列目には 2、上から 2 行目・左から 6 列目には 2 をかきます。

次に "ch" を探します (表の上から 3 行目)。s の 1 文字目は "c" なので、文字数の理由からここまでに "ch" はなく、表の上から 3 行目・左から 2 行目には 0 をかきます (このセルは s とは無関係に 0 になるので、下図ではグレーで塗りました。s の 2 文字目は "h" なので、2 文字目までに見つかった "ch" は 1 通りであり、表の上から 3 行目・左から 3 行目には 1 をかきます。s の 3 文字目は "c" なので、3 文字目までに見つかった "ch" は 1 通りのままであり、表の上から 3 行目・左から 4 行目には 1 をかきます。s の 4 文字目は "h" なので、4 文字目までに見つかった "ch" は 3 通りであり、表の上から 3 行目・左から 5 行目には 3 をかきます。同様にして、表の上から 3 行目・左から 6 行目には 3 をかきます。

最後に "cho" を探します (表の上から 4 行目)。これまでと同様の手順により、上から 4 行目・左から 2 行目は 0、上から 4 行目・左から 3 行目は 0、上から 4 行目・左から 4 行目は 0、上から 4 行目・左から 5 行目は 0、
上から 4 行目・左から 6 行目は 3 をかきます。最後に書き込んだ値 (黄色いセル) から、 s="chcho" の中に "cho" は 3 通りあることがわかります。

以上より、わかったルールは以下の通りです。
・(1行目)(1列目) s の 1 文字目が "c" なら 1、異なるなら 0
・(1行目)(2列目以降) 1 つ左のセルの値をコピーし、さらに対応する文字が "c" ならセルの値に 1 を加える
・(2行目以降)(1列目) s の内容にかかわらず 0
・(2行目以降)(2列目以降) 1 つ左の値をコピーし、さらに対応する文字が同じならば 1 つ上のセルの値を加える
そして最後のセルの値が問題の答えとなります。これをコードにすると以下のようになります。

abc0211c-1.cpp

#include <bits/stdc++.h>
using namespace std;
 
int main() {
  string s;
  cin >> s;

  string c = "chokudai";
  int nstring = (int)s.size();
  vector<vector<int>> nc(8,vector<int>(nstring,0));

  if ( s.at(0)==c.at(0) ) {
    nc.at(0).at(0) = 1;
  }
  for ( int j=1; j<nstring; j++ ) {
    nc.at(0).at(j) = nc.at(0).at(j-1);
    if ( s.at(j)==c.at(0) ) {
      nc.at(0).at(j) += 1;
    }
  }

  int MOD = pow(10,9)+7;
  for ( int i=1; i<8; i++ ) {
    for ( int j=1; j<nstring; j++ ) {
      nc.at(i).at(j) = nc.at(i).at(j-1);
      if ( s.at(j)==c.at(i) ) {
        nc.at(i).at(j) = (nc.at(i).at(j)+nc.at(i-1).at(j))%MOD;
      }
    }
  }

  cout << nc.at(7).at(nstring-1) << endl;
}

回答2 (AC)

回答1を改良します。上のコードを見て気づくのは、表の最初の行と次の行以降の処理が分かれていることです。表の計算ルールの大原則は「あるセルの値は左のセルの値をコピーし、文字が同じなら上のセルの値を加える」なので、最初の行の処理をこれに合わせるのが良いでしょう。それには、一番最初に新しい行を追加し、全ての値を 1 に設定しておきます。こうすることで、最初の行の処理を上記の大原則に揃えることができます。その分、行番号が 1 ずつずれることに注意が必要です。

2 つ目の改良は、各行で処理を開始するセルについてです。回答1の説明では最初のセルだけを自動的に 0 になるセルとして紹介しましたが、同様にその行で探したい文字列の長さより短い部分のセルは 0 になるので、行数が大きくなるにつれて処理を開始するセルはどんどん右にして良いことがわかります。

3 つ目の改良は、与えられた文字列 s において c, h, o, k, u, d, a, i 以外の文字は場合の数を計算する上では不要なので、これら以外の文字は削除しても構わないと言うことです。このテクニックは文字列に不要な文字が大量に存在する場合に効果を発揮しますが、このテクニックを使っていない回答1のコードで AC になったので、今回の問題ではこのテクニックは不要なことがわかります orz...)

以上を適用したコードは以下のようになりました。1 つ目の改良で期待したように、メイン処理部分のコードはすっきりしましたが、1 行目の各セルの値を 1
に設定する手間が増えたたため、コード量は変わりませんでした。ただし、本質的に同じ処理をするコードは 1 つにすべきなので、回答2のコードの方が可搬性は高いと思います。

abc211b-2.cpp

#include <bits/stdc++.h>
using namespace std;
 
int main() {
  string t;
  cin >> t;

  string s = "";
  for ( int i=0; i<(int)t.size(); i++ ) {
    if ( t.at(i)=='c' || t.at(i)=='h' || t.at(i)=='o' || t.at(i)=='k'
      || t.at(i)=='u' || t.at(i)=='d' || t.at(i)=='a' || t.at(i)=='i' ) {
      s += t.at(i);
    }
  }
  
  string c = "chokudai";
  int nstring = (int)s.size();
  vector<vector<int>> nc(9,vector<int>(nstring+1,0));
  for ( int j=0; j<=nstring; j++ ) {
    nc.at(0).at(j) = 1;
  }
  
  int MOD = pow(10,9)+7;
  for ( int i=1; i<9; i++ ) {
    for ( int j=i; j<=nstring; j++ ) {
      nc.at(i).at(j) = nc.at(i).at(j-1);
      if ( s.at(j-1)==c.at(i-1) ) {
        nc.at(i).at(j) = (nc.at(i).at(j)+nc.at(i-1).at(j))%MOD;
      }
    }
  }

  cout << nc.at(8).at(nstring) << endl;
}

調べたこと

AtCoder の解説 → 公式解説

回答1と同じでした。この解法は動的計画法(DP)と呼ばれる方法で、AtCoder において重要なアプローチのようです。

リンク

• 前の記事 → AtCoderログ：039 - ABC 144 B
• 次の記事 → AtCoderログ：041 - ABC 133 b