はじめに
この6か月間、私はデータサイエンティストになるべく、pythonを用いたデータ分析の勉強を実施しました。その集大成として、今回中古車価格の予測に挑戦しました。
実際にモデルを作ってみると、「これは確かに価格に効きそうだ」と感じる要素もあれば、「この変数が意外と効くのか」という新しい発見もありました。
本記事では、その過程と気づきを共有します。
解決したい社会問題
中古車価格は絶対的な指標がなく、価格の決定はブラックボックス化されています。そのブラックボックス化されている価格に影響を与える要素、および各要素の影響度合いのヒントを可視化すべく、データ分析を用いて検証しました。
分析するデータ
「Used Car Price Prediction Dataset」(市場における中古車価格)を用いて、データ分析を実施します。
実行環境
パソコン:Windows
開発環境:Google Colab(Google Colaboratory)
言語:Python
ライブラリ:Pandas, Numpy, Matplotlib, Seaborn, scikit-learn
分析の流れ
- モデリングに向けたライブラリの読み込み
- データのインポートとデータの確認
2.1 データのインポート
2.2 データの確認 - データの前処理
3.1 目的変数の正規分布化
3.2 相関の確認
3.3 外れ値の確認と処理
3.4 機械学習に向けたデータのグルーピング化 - モデリングに向けた準備
- モデリングとテストデータを用いた検証(XGBoost編)
- スコア改善に向けたモデリングとテスト(CatBoostRegressor編)
分析の過程
1.ライブラリの読み込み
#データ分析用
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
#統計用
from scipy import stats
from scipy.stats import norm, skew
#データ分割用
from sklearn.model_selection import train_test_split
#モデリング用
from xgboost import XGBRegressor
from catboost import CatBoostRegressor
from sklearn.model_selection import StratifiedGroupKFold
from sklearn.model_selection import KFold
from sklearn.metrics import mean_squared_error
2. データのインポートと中身の確認
2.1 データのインポート
データセットを読み込みます。
#データの読み込み
train = pd.read_csv(`/content/train.csv`)
test = pd.read_csv(`/content/test.csv`)
2.2 データの確認
trainデータにおけるデータの構造を理解すべく、具体的な中身を確認します。
train.head()
次にtrainデータに含まれているデータ項目や種類を確認します。
train.info()
90個あるデータのうち、82個をbool型のデータが占めておりますが、中にはcategoryやfloat, int64型のデータも含まれています。この状態でモデル学習に投入してもエラーが生じる可能性は低いと判断しました。
最後にtrainデータにおける定量データの分布を確認します。
※本trainデータでは「milage」「car_age」「motor_count」「horsepower」「engin_displacement」(いずれも説明変数)、および「price」(目的変数)の6つになります。
train.describe()
統計量から、以下のことを発見しました。
・全体的にデータの下位75%までは比例的、かつ緩く数値が増加している。この75%ラインを超えた最大値までの数値は一気に数値の増加が増大しており、データが極端に偏っている可能性がある。
・milage(走行距離数:単位mile)については全中古車の75%は100,000mile以内であるが、最大値は400,000mileと出ており、このような車の中にはcar_ageも大きい車である可能性がある。
・car_age(モデルが販売されてからの経過期間、単位:年)は75%が15年以内であるが、30年以上経過しているモデルも存在する。この中にはアメ車など、プレミアム化されている車も存在している可能性がある。
・motor(モーターの数)も基本的には1つだが、3つ備えている車も存在する。またhorsepower(馬力)についても最大値には1020馬力の車も存在しており、このような車はスポーツカーの可能性がある。
・engine_displacement(排気量:単位 L)については、75%は4.6L以内である。一方で8.4Lと出ているモデルもあり、これもスポーツカーのデータである可能性がある。
上記の各要素がpriceにどの程度影響するか、後ほど相関図で確かめることにします。
3. データの前処理
3.1 目的変数の正規分布化
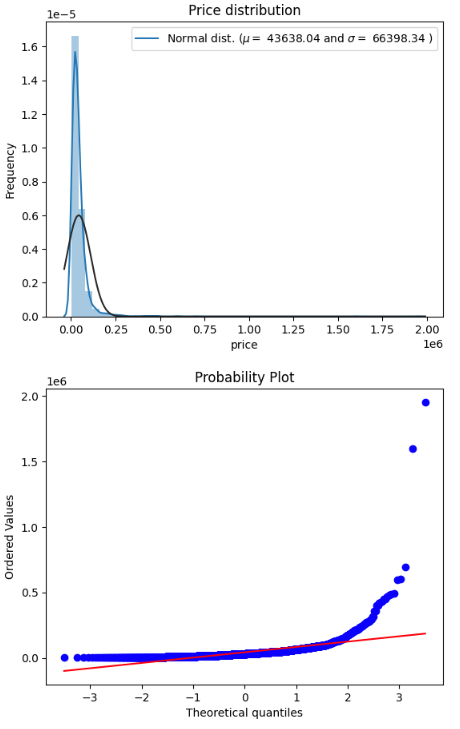
先ほどのtrainデータの統計量を確認した際に、priceの分布が極端に偏っている可能性があることを見出したため、グラフにて可視化します。
#priceデータのヒストグラム
sns.distplot(train['price'] , fit=norm);
# MLE(Maximum Likelihood Estimate)による分布の推定
(mu, sigma) = norm.fit(train['price'])
print('mu = {:.2f} and sigma = {:.2f}'.format(mu, sigma))
print('※muは、平均値。 sigmaは、標準偏差')
plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)], loc='best')
plt.ylabel('Frequency')
plt.title('Price distribution')
# QQプロット
fig = plt.figure()
res = stats.probplot(train['price'], plot=plt)
plt.show()
mu = 45318.00 and sigma = 87607.21
※muは、平均値。 sigmaは、標準偏差
上記のヒストグラムおよびQQプロットからPriceデータが右側に大きくゆがんでいることがわかりました。そこでlogを使って正規化させます。
# log(1+x)による対数変換
train["price"] = np.log1p(train["price"])
#ヒストグラムの描画
sns.distplot(train['price'] , fit=norm);
# MLE(Maximum Likelihood Estimate)による分布の推定
(mu, sigma) = norm.fit(train['price'])
print('mu = {:.2f} and sigma = {:.2f}'.format(mu, sigma))
print('※muは、平均値。 sigmaは、標準偏差')
plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)], loc='best')
plt.ylabel('Frequency')
plt.title('Price distribution')
# QQプロット
fig = plt.figure()
res = stats.probplot(train['price'], plot=plt)
plt.show()
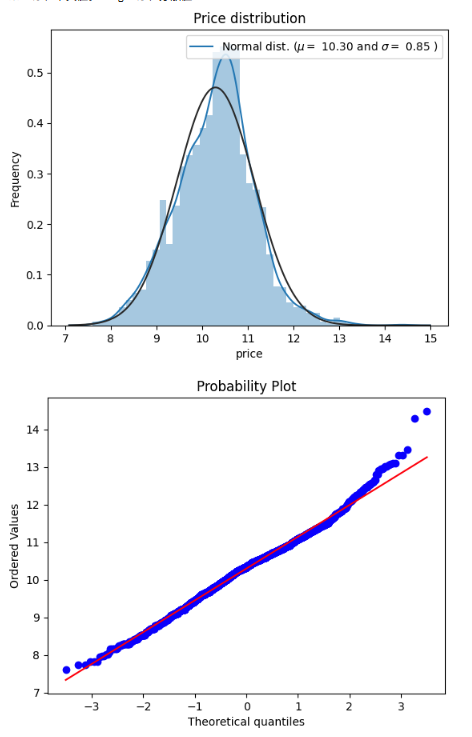
mu = 10.30 and sigma = 0.86
※muは、平均値。 sigmaは、標準偏差
priceデータが正規分布化していることを確認できました。このデータをもとに、機械学習を実行します。
3.2 相関の確認
正規化されたPriceと各説明変数との相関を確認します。なお説明変数が89個と多数になるため、上位20位の説明変数との相関を確認します。
corr = train.corr(numeric_only=True)
target = 'price'
corr_target = corr[target].abs().sort_values(ascending=False)
#上位20項目との相関を表示
top20 = corr_target.head(20)
print(top20)
#相関図
#先ほど作成した「top20」は2次元の行列でないことから、行列に変換
cols = top20.index
corr_sub = train[cols].corr()
plt.figure(figsize=(40, 40))
sns.heatmap(corr_sub, annot=True)
相関係数表や相関図から、以下を発見しました。
・priceと相関が顕著に強い説明変数は、milageとcar_ageである。
・高級車ブランドであるか否かは、中古車価格の決定要素として影響している。
・内装/外装の色では、gold/beige、silver/grayであるか否かはpriceに影響を与える要素になる。
3.3 外れ値の確認と処理
priceと特に相関の強いmilageとcar_ageについて、機械学習への影響を最小限に抑えるために、外れ値の有無を確認します。
#milage
fig, ax = plt.subplots()
ax.scatter(x = train['milage'], y= train['price'])
plt.ylabel('Price', fontsize=13)
plt.xlabel('Milage', fontsize=13)
plt.show()
#car_age
fig, ax = plt.subplots()
ax.scatter(x = train['car_age'], y=train['price'])
plt.ylabel('Price', fontsize=13)
plt.xlabel('Car_Age', fontsize=13)
plt.show()
milageが300000以上であるにも関わらず、priceが8以上となっている車が4台存在します。
car_ageが50年前後の車であるにも関わらず、価格が比較的高い車が1台、そしてcar_ageが10-20年経過している車のうち、価格が平均よりも高い車が3台存在します。
これらの車の特徴を確認し、有意義な外れ値か単なる異常値かを判断します。
まずMilageにおいて平均以上のpriceを出している車について確認します。
#milageが300000以上かつpriceが8以上の車
HM_car = train[(train['milage']>300000) & (train['price']>8)]
HM_car
Hondaを除いた4台は高級ブランド車であることから、milageが大きくなってもプレミア価格がついている可能性はがあります。Honda車についてはmilageが大きい(405,000mile)ものの、事故や災害にあった記録がないことから、大衆車であっても価格が維持されている可能性があります。Honda車のデータは機械学習において誤った学習を招く可能性があることから、milageの上限値を400,000としてクリップ化処理を実施し、学習データから外します。
train['milage'] = train['milage'].clip(lower=0, upper=400000)
続いてcar_ageにおいて平均以上のpriceを出している車のデータについて確認します。
#car_ageが10以上、かつpriceが14以上の車
High_car = train[(train['car_age']>10) & (train['price']>14)]
High_car
#car_ageが40以上の車
Old_car = train[train['car_age']>40]
Old_car
上記の4台についてはすべて高級ブランド車であることから、平均よりも高値で売却されていると予測がつくため、異常値と処理せず残します。
以上でデータの前処理が終わりました。前処理では説明変数の削除を実施しなかったため、89個
4. モデリングに向けた準備
モデリングに向けて、学習データ・テストデータの説明変数と目的変数を設定します。
#trainデータ
X_train = train.drop('price', axis=1)
y_train = train['price'] # log 変換後の y
#testデータ
X_test = test.drop('price', axis=1)
y_test = np.log1p(test['price'])
モデリング前に、学習データで実際に投入するX_trainの最初の5行のデータを確認します。上述のコードが正しく実行されていれば、目的変数であるpriceのないデータになっています。
X_train.head()
X_trainは、priceがdropされたデータであることを確認できました。
また今回のモデルではstratifyによるkfold分割を用いるため、分析に向けて必要な設定をします。
#stratify用に価格帯をビン分割
y_bins = pd.qcut(y_train, q=8, duplicates='drop').astype(str)
#「model」を機械学習のグループ化に向けた要素として用いる
groups = X_train['model']
ここまで機械学習に向けた準備は整いました。では、本題の機械学習に移ります。
5. モデリングとテストデータを用いた検証(XGBoost編)
モデル分析について、まずはXGboostによる検証を実施します。XGBoostはツリー系アルゴリズムとして外れ値にも強い特性を持っていることから、今回の機械学習に採用しました。結果にはRMSEを用いて、モデルの正確性を確認します。
kf = StratifiedGroupKFold(n_splits=5, shuffle=True, random_state=0)
rmse_scores = []
#学習データをさらに訓練データと検証用データに分割
for train_idx, val_idx in kf.split(X, y_bins, groups):
X_tr, X_val = X_train.iloc[train_idx], X_train.iloc[val_idx]
y_tr, y_val = y_train.iloc[train_idx], y_train.iloc[val_idx]
#XGBoostのモデル
#モデルの詳細をここで設定
model = XGBRegressor(
n_estimators=2000,
learning_rate=0.03,
max_depth=8,
subsample=0.8,
colsample_bytree=0.8,
objective='reg:squarederror',
tree_method='hist',
eval_metric='rmse',
enable_categorical=True,
random_state=0
)
#訓練データを使って、モデルに学習させる
model.fit(X_train, y_train)
#実証データによる予測用にlog変換されているyをもとの生データに戻す
preds = np.expm1(model.predict(X_val))
true = np.expm1(y_val)
#RMSEの設定
rmse = np.sqrt(mean_squared_error(true, preds))
rmse_scores.append(rmse)
#Kfold RMSEおよびFold-wiseの算出
print("KFold RMSE:", np.mean(rmse_scores))
print("Fold-wise:", rmse_scores)
KFold RMSE: 23743.17266298445
Fold-wise: [4848.288969219486, 85452.53693697568, 14594.76339470648, 8666.914456869732, 5153.359557150858]
各KFoldごとのRMSEスコア(各グループにおける検証データでの予測と本当の結果との誤差)は、ほぼすべてのデータで10,000以内に収まりました。これは誤差が10,000ドル未満で収斂していることを意味します。一方で1つのKfoldのみ、RMSEが80,000と誤差が大きくなりました。これはモデルがcar_ageやmilageの高いブランド車といった「回帰線通りに価格が当てはまらない車」の価格をうまく予測できないことを示している可能性があります。
この弱点が、テストデータにおいてどの程度影響が出るかを確認します。
#RMSEを用いて、テストデータにおける誤差を確認
#予測を実施
pred_log = model.predict(X_test)
#逆変換して「本当の価格」に戻す
pred = np.expm1(pred_log)
true = np.expm1(y_test)
#テストデータにおける予測結果とテストデータにあるpriceデータに対するRMSEを算出
rmse_test = np.sqrt(mean_squared_error(true, pred))
print("Test RMSE:", rmse_test)
Test RMSE: 32553.837881663356
XGBoostではテストデータで記録されているpriceとモデルによる予測結果に約32,553ドルの誤差が発生しています。つまりモデルの予測価格が、実際の中古車価格と平均して約3万2000ドル程度ずれていることを意味します。先ほどのモデルの弱点も影響している可能性はありますが、この誤差は異なるアルゴリズムを用いることで縮める可能性もあるため、次の章で同じツリー系アルゴリズムのCatBoostを用いて改善を試みます。
6. スコア改善に向けたモデリングとテスト(CatBoost編)
CatBoostはXGBoostと同じツリー系アルゴリズムですが、XGBoostよりもさらに過学習を防ぎながら、精度の高いモデル学習・分析が期待できます。
kf = StratifiedGroupKFold(n_splits=5, shuffle=True, random_state=0)
rmse_scores = []
#学習データをさらに訓練データと検証用データに分割
for train_idx, val_idx in kf.split(X_train, y_bins, groups):
X_tr, X_val = X_train.iloc[train_idx], X_train.iloc[val_idx]
y_tr, y_val = y_train.iloc[train_idx], y_train.iloc[val_idx]
#モデルの詳細を設定
model2 = CatBoostRegressor(
iterations=2000,
learning_rate=0.03,
depth=8,
loss_function='RMSE',
eval_metric='RMSE',
cat_features=[‘brand’, ‘model’],
verbose=False
)
#訓練データを使って、モデルに学習させる
model2.fit(X_train, y_train)
#予測用にlog変換されているyをもとの生データに戻す、そのうえで検証データによる予測を実施
preds = np.expm1(model2.predict(X_val))
true = np.expm1(y_val)
#RMSEの設定
rmse = np.sqrt(mean_squared_error(true, preds))
rmse_scores.append(rmse)
#Kfold RMSEおよびFold-wiseの算出
print("KFold RMSE:", np.mean(rmse_scores))
print("Fold-wise:", rmse_scores)
KFold RMSE: 23009.709316016604
Fold-wise: [3342.5052574711567, 83838.56774611538, 13093.0700440566, 8681.075119538144, 6093.32841290174]
全体的に誤差が縮小しており、精度が改善しています。このモデルでテストデータにおける予測も実行します。
#RMSEを用いて、テストデータにおける誤差を確認
#予測を実施
pred_log = model2.predict(X_test)
#逆変換して「本当の価格」に戻す
pred = np.expm1(pred_log)
true = np.expm1(y_test)
#テストデータにおける予測結果とテストデータにあるpriceデータに対するRMSEを算出
rmse_test = np.sqrt(mean_squared_error(true, pred))
print("Test RMSE:", rmse_test)
Test RMSE: 31911.273716615546
考察
CatBoostを用いた機械学習では、テストデータにおけるRMSEが32,000ドルを切り、XGBoostよりも改善していることが確認できました。初回の機械学習としては良いスコアを出すことができました。
課題
今後さらにスコアを改善するべく、例えば以下の方法が考えられます。
・データの前処理の段階で、価格帯別でデータをグルーピング化する
・回帰線から外れるデータ(特にmilageやcar_ageが多くても、高値が付くブランド車)について別でモデルに学習させる
上記の改善施策を通じて、より精度が高く、かつ社会で役立つ実用的なモデルを作り上げていく予定です。
まとめ
今回中古車市場における価格の決定要素を探すべく、分析を実施しました。
・中古車価格に特に影響を与える説明変数は milage(走行距離) と car_age(モデル発売からの経過年数)である。
・事故・罹災の有無も価格に影響する要素である。
・内装・外装の色では gold/beige, silver/gray が価格を押し上げる要因になっている。
・高級車ブランド(Lamborghini, Porsche, Bugatti, Rolls-Royce など)は、 mileage / car_age が大きくても平均より高値で取引される可能性がある。
「milage や car_age、高級ブランドか否か、事故や罹災の有無が price に影響する」という点については、予測がつく要素であり、今回のモデル結果を踏まえても確かに妥当な結果と考えました。
一方で内装・外装については、gold/beige, silver/grayの色であるか否かが価格に影響する主力の要素となる点には驚きました。日本に限るかもしれませんが、たいてい中古車としてのリセールが高くつく色(外装に限りますが...)は、白や黒といったモノトーン色と言われており、実際に日本を走る車も白や黒色が多い印象があります。今回の中古車価格のデータでは、白・黒以外の色が価格を左右する要素として入っていることから、市場が展開される国ごとにリセールの価値の高い色が異なる可能性もあると言えます。これは興味深い発見であり、今後の分析にも生かす予定です。
今後のデータ分析ではモデルの精度を上げるべく、例えばデータの前処理を工夫したり、今回取り扱った説明変数以外の要素を取り入れて、より最適な機械学習を実施する予定です。またランダムフォレストなど異なる種類のアルゴリズムを用いて、モデルの精度の改善度合いについても確認し、より実用的な中古車価格予測モデルを作成していきます。そして最終的にはブラックボックス化されている中古車価格の決定要素を可視化し、例えばアプリでモデルや走行距離数、外装や内装に色等の要素を入力するだけで、簡単に中古車価格が予測できるシステムの構築や、企業向けに最適な中古車売却戦略の立案に向けたデータ提供にもつなげていきたいと思います。