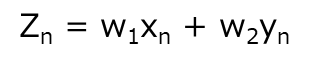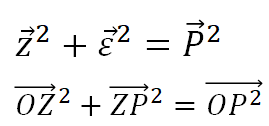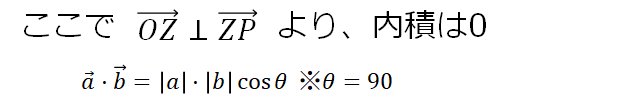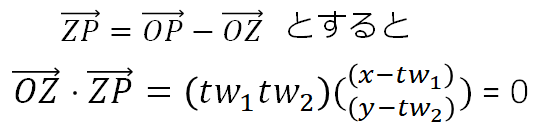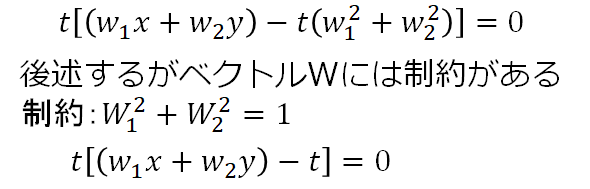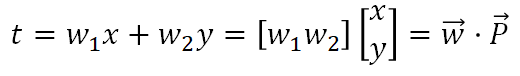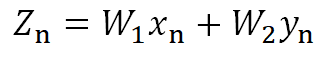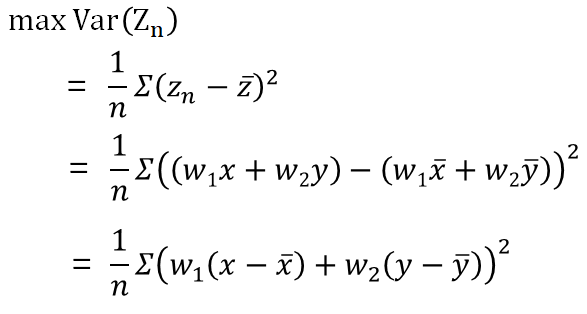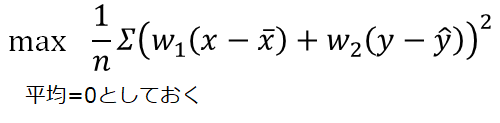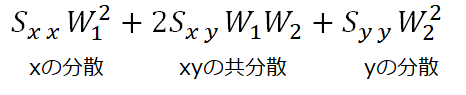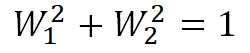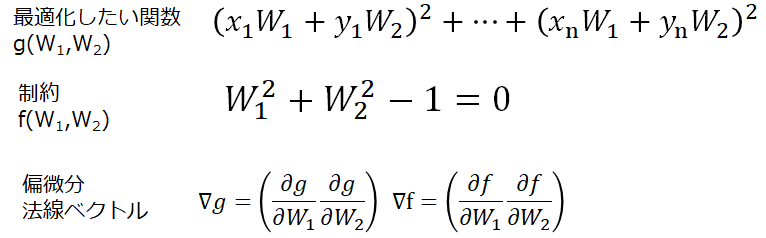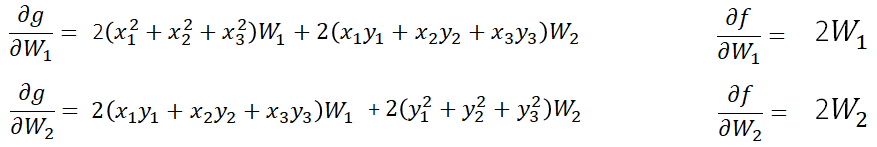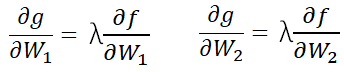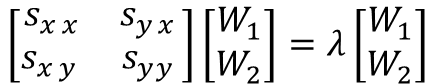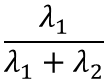More than 3 years have passed since last update.

図でわかる主成分分析【数式理解も。】

Posted at 2020-07-03

#主成分分析といえば

・多次元のデータから主要な成分を抽出(主成分)
・次元が増えすぎることによる問題を解決(次元削減)
・多次元データで主要成分から外れる値を見つける(異常検知)
・メモリを圧迫するデータを削減
・などなど...
様々な目的に使われる主成分分析ですが、
その数学的な背景は統計や解析・線形代数の知識が必要であり、
単にライブラリやパッケージだけを使っていては、
なかなか気にしないし親しみが無いものだったりする。

理論的な背景を知ることで、**「なぜ主成分分析でうまくいかなかったのか」**といった原因が見つかるかもしれない。

そこでなるべく図を用いてわかりやすくやっていることを説明したいと思う。

#主成分分析で実現しようとしていること

上記にも挙げたが、主成分分析とはまさに「主成分」を抽出してその関係性について考察できるようになるツールである。
その抽出方法とは、データの持つ関係性に注目して、各データ点を新たな軸に移すというものである。
多次元の場合各次元から一つの軸に抽出する、という過程は想像しにくい(と思う)ので、本記事では二軸の場合で説明を進める。

##データの関係性の抽出

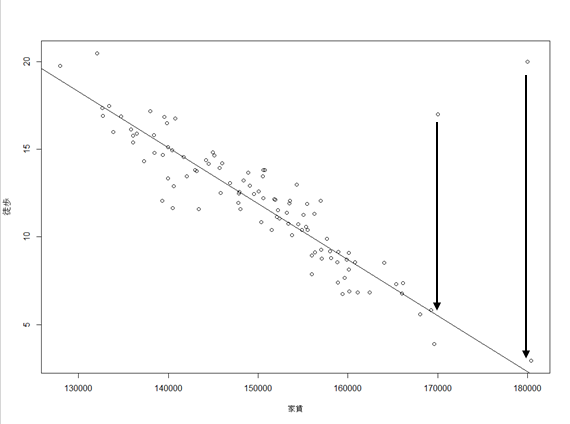
関係性から離れることになるが、線形回帰は予測モデル(図中黒線)と各データ点との距離が最小になるように学習する手法であった。
このように学習することで、データのなるべく中心(平均)を通るように予測モデルが引かれる。
線形(直線で表現できる)関係のデータであれば、データ点が増えれば増えるほど求めるべき真のモデルに近づいていく。

線形回帰は
・x軸が予測に使うもの
・y軸が予測対象
であったのに対して
主成分分析はというと、
・x軸もy軸も予測に使うもの
である。

つまり重回帰の際にいくつかの変数を使うが、この変数だけに限って注目した分析になる。
"変数を減らす"とは各変数間の関係性を表すような新しい軸を作る事で達成しようとする。
また、線形回帰との違いは、各変数の関係性の抽出であるため、各データ点と線の法線の距離を最小にするように学習させる。
これについて例を挙げて説明する。

##関係性を表す軸

例えば**「新宿駅付近に住んでいる人」の年収を予測したいと考えたとする。
手元には年収,住んでいる住居の家賃,駅からの徒歩時間**のデータがある。

軽率な考えだが、家賃が高く新宿駅に近い人が年収高いというのが本当の因果としよう。

ここで
・重回帰を使うと死んでしまう病気
・二変数は扱えない予測システム
・二変数も保存しておくメモリ容量が無い
・この二変数ではうまく予測ができなかった
など特殊な事情から、家賃と徒歩時間の両方を保持しておくのは難しいとする。
どちらか片方を捨てるのも勿体ない。
せっかく保存しているデータはなんとか活用したい。

そこで新しい軸に移し替えてやることにする。

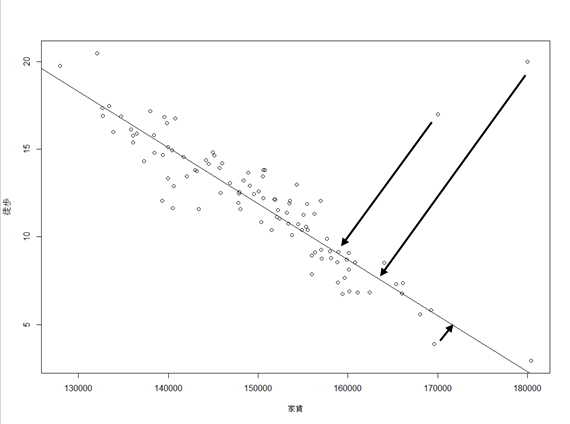
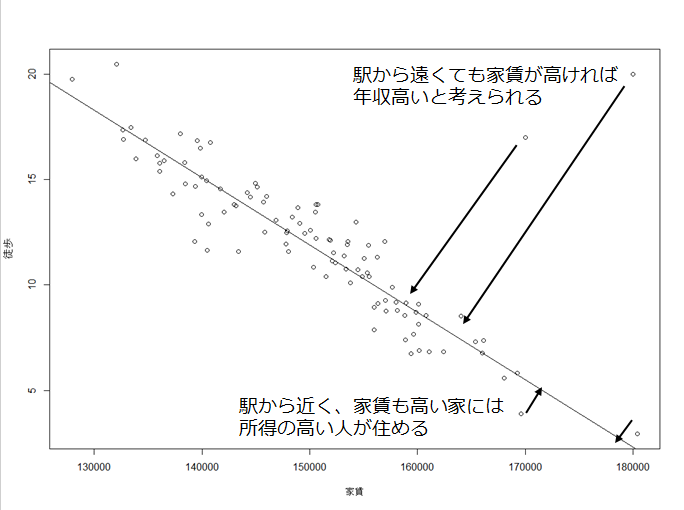
新しい軸の右側(図では線がナナメなので右下)に移されたデータたちを
「イケてる生活をしている人ランキング」として勝手に解釈しよう。
・家賃・駅近どちらも満たしている人はランキング上位である
・家賃が高くても駅から遠い人はあまり活動的でないのかもしれない。しかし家賃がものすごく高いのならばたとえ駅に近くなくともイケてる生活をしているかもしれない
このようなランキング(順序)関係を法線を下した軸にデータを移すことで得たとする。

こうして作り出した軸を「主成分軸」と呼ぶことにする。

##ただ線を引くだけではない

むやみに線を引いて「主成分軸」を考えればいいというものでもない。
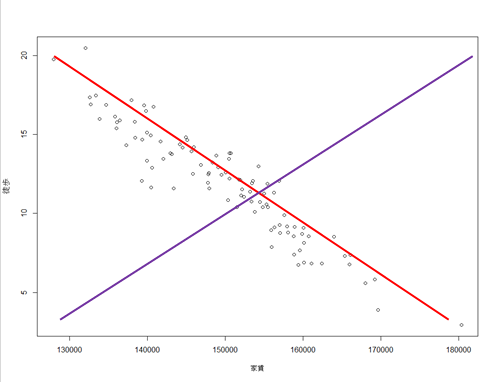
例えばデータから法線が引ける線は色々あるが以下の2色の線を考える。
どちらの線のほうが**「元の変数の関係性を表せているか」と聞かれたら、
赤色の線のほうが関係性を表していそうだ、と答えるのは自然なことと思う。
このような"関係性"というものは統計学では"相関係数"や"共分散"**というもので表現される。

変数の値は共に増えるのか
共に減るのか
片方が増えて片方が減る関係なのか
などが表現できる指標である。

##2色の線のちがい

赤色の線のほうが関係性が抽出できていそう、
というのは感覚的にわかってもらえると思うが、
もう少し掘り下げてみる。

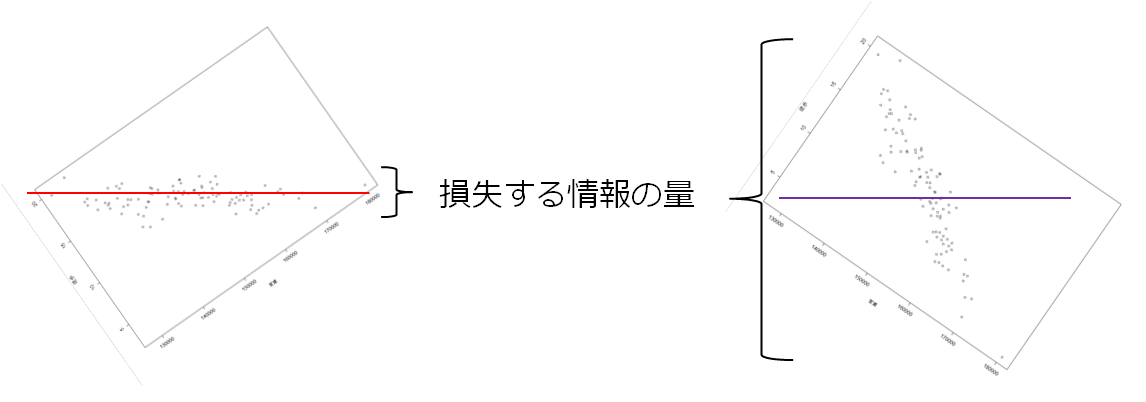
ハイレゾ高画質で録画したTV番組も容量の関係でエンコードしなければならない時と同じように
「二つの変数が使えず、一つの変数にするしかない」
と言われたら何とか元データを余すことなく抽出したい気持ちになる。
そこで元データから損失してしまうデータを最小にしようと考える。

また、この損失を抑えるという目標は、主成分軸上のデータの分散を最大にするということに他ならない。
私はこの分散の最大化と情報損失の考え方がイマイチピンとこなかったのでもっと深堀していく。

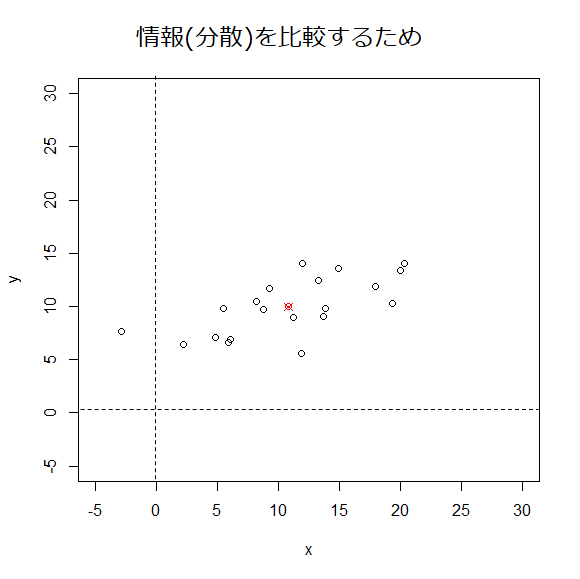
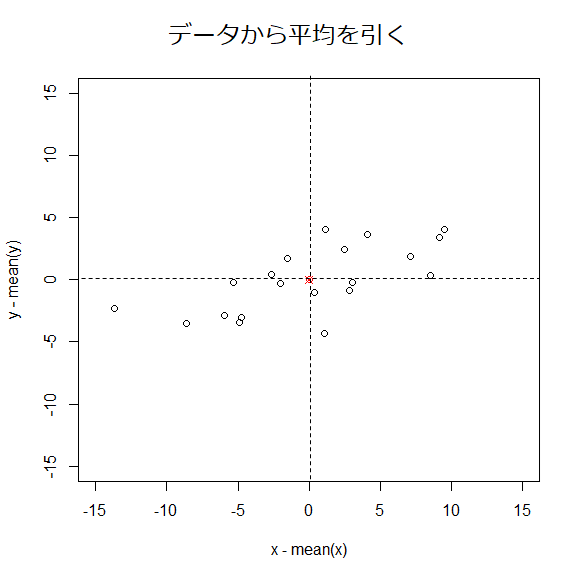
##少し前処理

相関係数や分散の計算を知っている人ならば各変数から平均値を引くことは理解してもらえると思う。
理解できなければ計算簡単のために引いていると一旦思ってほしい。

こうして平均を0にしたデータに前処理してやる。

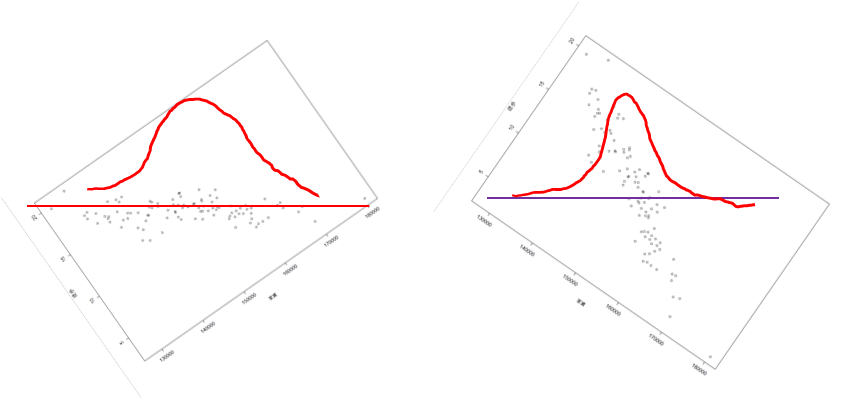
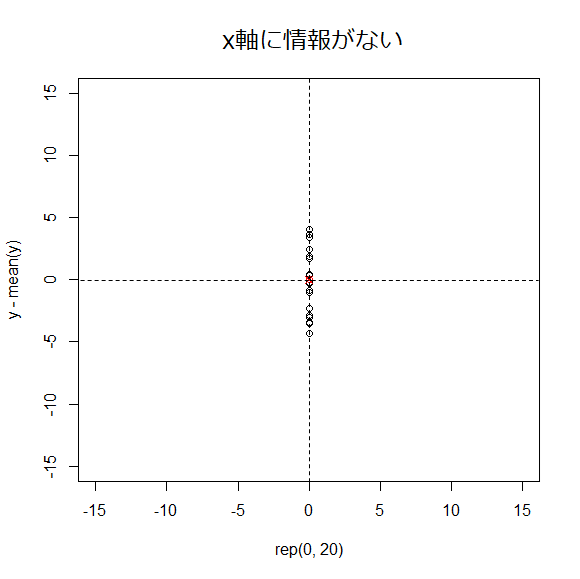
##分散は情報なのか？

情報(分散)と図中に書いていたが、「分散がある」と「情報」とはどういう意味かというと
下図のように分散が無いデータだったらどうなるか、と考えた時、
分散の無いデータでは新しい軸を引くまでもなく、元の軸は必要がなくなるから、
分散のことを**情報(少なくとも何か関係性を持っている)**として考える。

##主成分軸の作り方

さて、データの関係性についての議論をしてきたので、
実際に主成分軸を数式的にはどのように作るのか説明していく。
まず二軸の値に何か係数を使い、主成分軸Zのある一点の値に直してやるなら、
以下の式が考えられる。

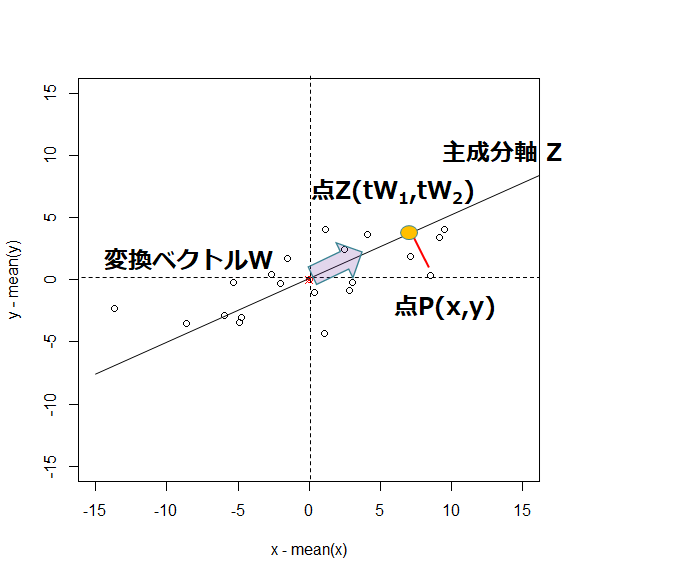
ここから高校数学のベクトル計算を思い出してほしい。

点P(x,y)を考えた時、原点Oから点PまでをベクトルP(P→)を、ベクトルWによってWの延長線上のある点Zに移すことを考える。
点Zを得るためにはベクトルWとベクトルPの積を計算する。

また、この図を幾何的に考えるとOPZは直角三角形である。
直角三角形にはピタゴラスの定理が使えるので、

が成り立つ。
これらの関係を数式にすると

と表現できる。
直交するベクトルの内積は0になるという性質を思い出して、

この性質と、ベクトルの引き算よりZPを計算して、組み合わせることで

これを展開して式整理すると、

上式の解の候補に0が出てくるが、0倍するとすべての点を原点に移す処理になってしまうので
0は解として不適切。t倍の値をもう一つの解から求めると、

よって内積の値で主成分軸の値に変換できることがわかった。

##もう一度、情報損失の最小化について考える

ピタゴラスの定理から情報の損失、つまりベクトルε(ベクトルZP)を最小にすることが目的となる。
原点Oから点Pまでの距離は既に得られているデータなので変えようがない。
この条件の下でベクトルεを小さくするにはベクトルZを大きくすることで対応するしかない。
今、前処理によって平均は0にしてあった。
Zの値も平均は0であり、「Zの二乗」これは「主成分軸の値の分散」に等しい。

つまり「情報の損失を抑える」とは「分散を最大にする」という事に等しくなることがわかる。

##分散の最大化から主成分軸を計算

ここで情報損失を抑えることが、分散の最大化であると理解できたので
分散最大化の問題を考えてみる。