正規分布は親しみ深い。
カイ二乗分布とt分布も検定の時には使う。
でもこれらがどんな関係か気になったことってありますか??
本記事ではこの関係性をRを使いながら確かめていこうと思います。
統計検定2級 2017年の問題を例に視覚的に解説していきます。
正規分布とカイ二乗分布の関係
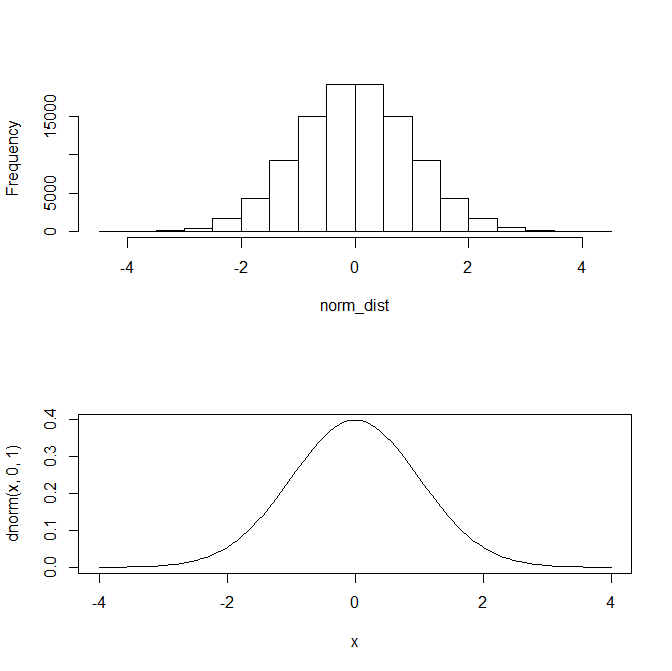
標準正規分布に従う確率変数 Z があるとする。
Z \;\;\;\; folloes \;\;\;\; N( \mu = 0 , \sigma = 1)
norm_dist <- rnorm(100000,0,1)
par(mfrow=c(2,1))
hist(norm_dist,main="")
curve(dnorm(x,0,1),-4,4)
確率変数Zが標準正規分布に従うとは、
Zの値は以下の図のような標準正規分布から取り出されるという意味。
標準正規分布からいくつかのデータを取り出す。
Z_{1}, Z_{2}....Z_{n}
のように n 個取り出す。
このZの2乗の総和を W とする
W = Z_{1}^2 + Z_{2}^2 + .... + Z_{n}^2 \\
W = \sum_{k=1}^{n} Z_{k}^2
この W は カイ二乗分布 に従う。
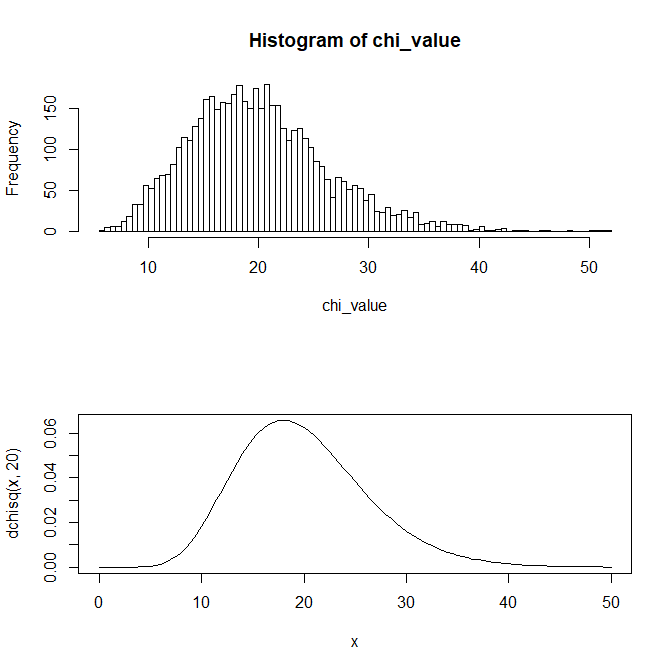
例えば n = 20 として、20個のデータを取り出すとする。
するとWは自由度20のカイ二乗分布に従う値となる。
sampling_norm_dist_by_20 <- matrix(norm_dist, length(seq(1,100000,20)), 20)
chi_value <- rowSums(sampling_norm_dist_by_20^2)
hist(chi_value,breaks = 100)
curve(dchisq(x,20),0,50)
また、ZがWと独立ならば
\frac{Z}{\sqrt{\frac{W}{n}}}
は自由度 n のt分布に従う。
sampling_norm_dist_by_20 <- matrix(norm_dist, length(seq(1,100000,20)), 20)
chi_value <- rowSums(sampling_norm_dist_by_20^2)
chi_value_sqrt <- sqrt(chi_value/20)
Z <- rnorm(length(chi_value_sqrt),0,1)
tdis <- Z / chi_value_sqrt
hist(tdis,xlim=c(-2,2),breaks=100)
curve(dt(x,20),-2,2)
話は少し戻って、Wは自由度nのカイニジョウ分布に従うのだった。
自由度m1のカイニジョウ分布に従うW1と、
自由度m2のカイニジョウ分布に従うW2があった時、
以下で計算される値は自由度(m1,m2)のF分布に従う。
\frac{\frac{W_{1}}{m_{1}}}{\frac{W_{2}}{m_{2}}}
これを確かめるために先ほどの自由度20のカイ二乗分布のほかに、自由度5のカイ二乗分布を用意する。
norm_dist_2 <- rnorm(100000,0,1)
sampling_norm_dist_by_5 <- matrix(norm_dist_2, length(seq(1,100000,5)), 5)
chi_value_2 <- rowSums(sampling_norm_dist_by_5^2)
hist(chi_value_2,breaks = 100)
curve(dchisq(x,5),0,25)
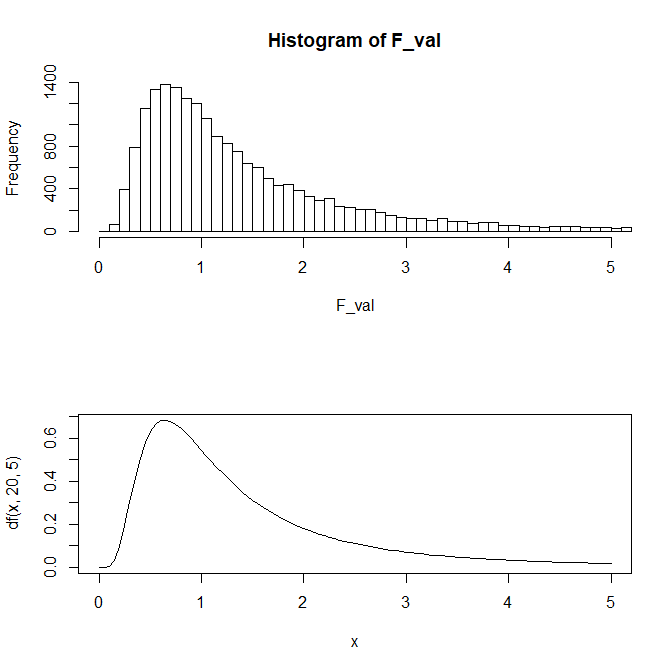
二つのカイ二乗分布から得られた値を計算すると、自由度(20,5)のF分布になる。
val_1 <- chi_value / 20
val_2 <- chi_value_2 / 5
F_val <- val_1 / val_2
hist(F_val,breaks=1000,xlim = c(0,5))
curve(df(x,20,5),0,5)
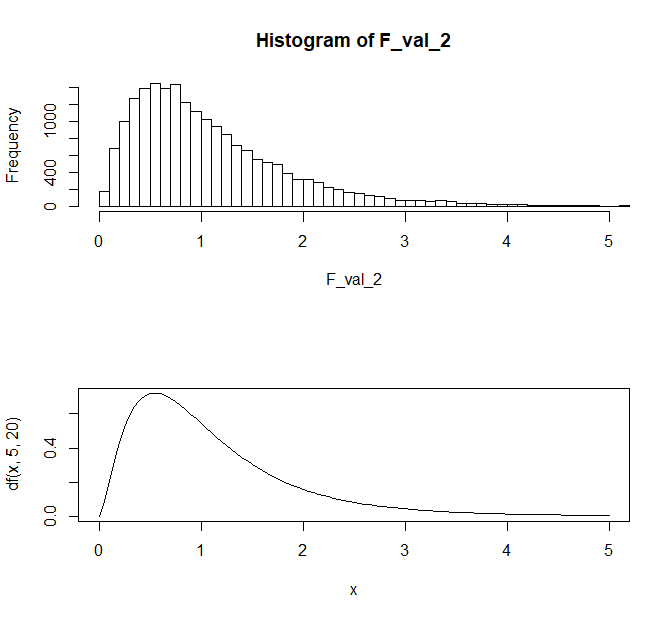
分子と分母を入れ替えると自由度の順番も入れ替わる。
par(mfrow=c(2,1))
val_1<-chi_value/20
val_2<-chi_value_2/5
F_val_2<-val_2/val_1
hist(F_val_2,breaks=100,xlim = c(0,5))
curve(df(x,5,20),0,5)
関係はここまで
ついでにF分布の優位水準についての問題を考える。
標準正規分布に従う値Zが30個ある。
各Zを二乗した値を20個と10個に分ける。
こうして2グループに分けたZの値を以下のように計算するとF分布に従う値が得られる。これをYとおく。
m_{1} = 20 \\
m_{2} = 10 \\
W_{1} = Z_{1}^2 + Z_{2}^2 + .... + Z_{20}^2 \\
W_{2} = Z_{21}^2 + Z_{2}^2 + .... + Z_{30}^2 \\
\quad \\
\quad \\
Y = \frac{
\frac{W_{1}}{m_{1}}}{
\frac{W_{2}}{m_{2}}}
bind_Y <- NULL
bind_inv_Y <- NULL
for(i in 1:10000){
test <- rnorm(30,0,1)
bunshi <- sum(((test[1:20])^2)/20)
bunbo <- sum(((test[21:30])^2)/10)
Y <- bunshi/bunbo
bind_Y<-c(bind_Y,Y)
"Y~ df(x,20,10)"
bind_inv_Y<-c(bind_inv_Y,(1/Y))
"1/Y~ df(x,10,20)"
}
par(mfrow=c(2,2))
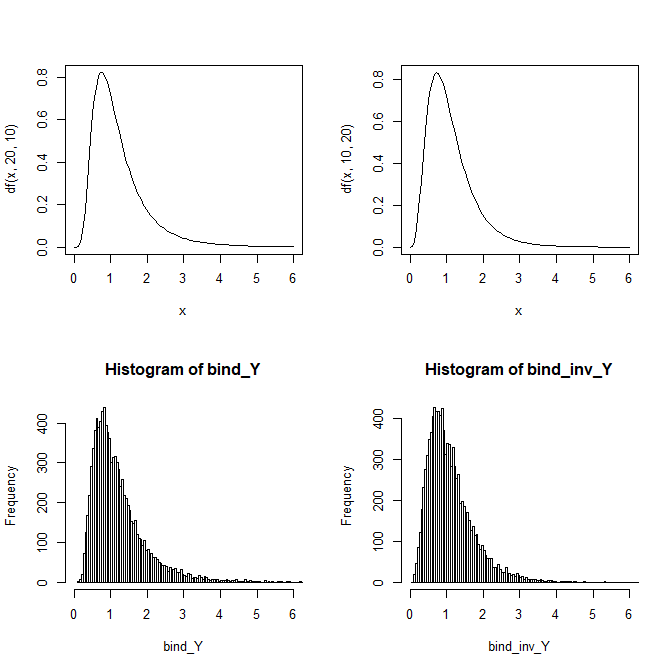
curve(df(x,20,10),0,6)
curve(df(x,10,20),0,6)
hist(bind_Y,breaks = 200,xlim = c(0,6))
hist(bind_inv_Y,breaks = 200,xlim = c(0,6))
左側が上式で定義した Y ※自由度(20,10)のF分布。
右側が分母と分子を入れ替えた物 ※自由度(10,20)のF分布。
問題としてこのYのF分布に対して
P( Y < \alpha) = 0.05
となるαはいくらか?という問題が来たとする。
F分布は上側確率についてのα=0.05のF分布表が用意されていたとする。
https://web.ma.utexas.edu/users/davis/375/popecol/tables/f005.html
求めたいのは下側の確率分布の面積が0.05となるような位置である。
Yの値は分数で与えられているので、分子と分母を逆にしてやると
Y = \frac{
\frac{W_{1}}{m_{1}}}{
\frac{W_{2}}{m_{2}}} \\
\frac{1}{Y} = \frac{
\frac{W_{2}}{m_{2}}}{
\frac{W_{1}}{m_{1}}}
逆転させたことによって、
P( Y < \alpha) = P( \frac{1}{Y} > \frac{1}{\alpha})
として、1/Y という値が自由度(10,20)のF分布の上側5%の範囲に入るには2.35という値よりも大きくならなければならない(より正確には2.348)。
\frac{1}{\alpha} = 2.35
なので、αを求めるには2.35を逆数にする。
つまり、P( Y < α) = 0.05 となるαは
\frac{1}{2.35}
である。
curve(df(x,10,20),0,6)
abline(v=2.348)
curve(df(x,20,10),0,6)
abline(v=1/2.348)
左側の図で2.35の地点に線を引くと、縦線 = 2.35 よりも上側(右側)の面積はおよそ5%ほど。
右側の図で 縦線 = 1/2.35 の地点を見ると下側(左側)の面積がおよそ5%ほどになっていそうなのが分かる。
おわり
統計二級の問題解説になってしまった。