検定は問題の「場合分け」と「使う数式」を覚えればテストは解ける。
しかし、性分からか本当の意味で統計を知っている状態で使って問題を解きたい、と考えてしまう。
統計は「考え方」を一度理解しておくと応用が利く場面というのは多いので、しっかりとした理解をしていきたいとおもい、勉強ついでに記事にした。
母平均の差の検定
問:鉛筆工場Aと鉛筆工場Bから作られた鉛筆をいくつか抜き出してチェックしていた。
Aから作られた鉛筆は平均的な長さ10.2 cm
Bから作られた鉛筆は平均的な長さ10.0 cmだった。
これは抜き出した鉛筆が偶然ちょっと長さが違ったのか?工場に問題があるのか?
このような時には、工場の作る鉛筆の長さ「母平均」が異なっているかを推定する問題となる。
単純に教科書を参考に解くだけならば、母分散が「既知」か「未知だが等しいことが分かっている」か「未知で等しくないと考えられる」の場合分けで計算する。
既知ならば、正規分布の再生性を応用して検定する。
未知だが等しいならば、正規分布の再生性とプールした分散を使う。
未知で等しくないならば、正規分布の再生性と補間法を利用してwelch's testを使う。
ここでまず「正規分布の再生性」という考えは、どの場合にも登場する言葉である。
統計検定の公式テキスト・問題集では、「正規分布の再生性より成り立つ」という一言で進んでしまうのだが、いったい何のことなのか気になったので深堀することにした。
問題を単純に解くだけならば
一番簡単な「母分散が既知」の場合で説明をする。
二つの鉛筆の長さは正規分布に従う値である。
工場Aの正規分布は
N(\mu_A,\sigma^2_A)
工場Bの正規分布は
N(\mu_B,\sigma^2_B)
であるとする。
もし、工場A,Bの鉛筆の平均的な長さに差は無いのであれば、理論的には
\mu_A - \mu_B = 0
となるはずである。
ただ、多少のばらつきはあるのでぴったり0になることは無く、少しばらつくと考えられる。
つまり、平均0として少しばらつく分布になることが想定される。
仮にこの値をdとおく。
d = \mu_A - \mu_B
正規分布ではこのようにして、
正規分布に従う値同士を計算したdもまた、正規分布に従うという性質を持つ。
このような、
「確率分布から得られた確率変数を計算して得られた値もまた同じ確率分布に変換される性質」
を「再生性(reproductive property)」と呼んでいる。
Rを使って「再生性」を確認
値X,Yがあり、正規分布に従うとする。
X \sim N(\mu_1, \sigma^2_1) \\\
Y \sim N(\mu_2, \sigma^2_2)
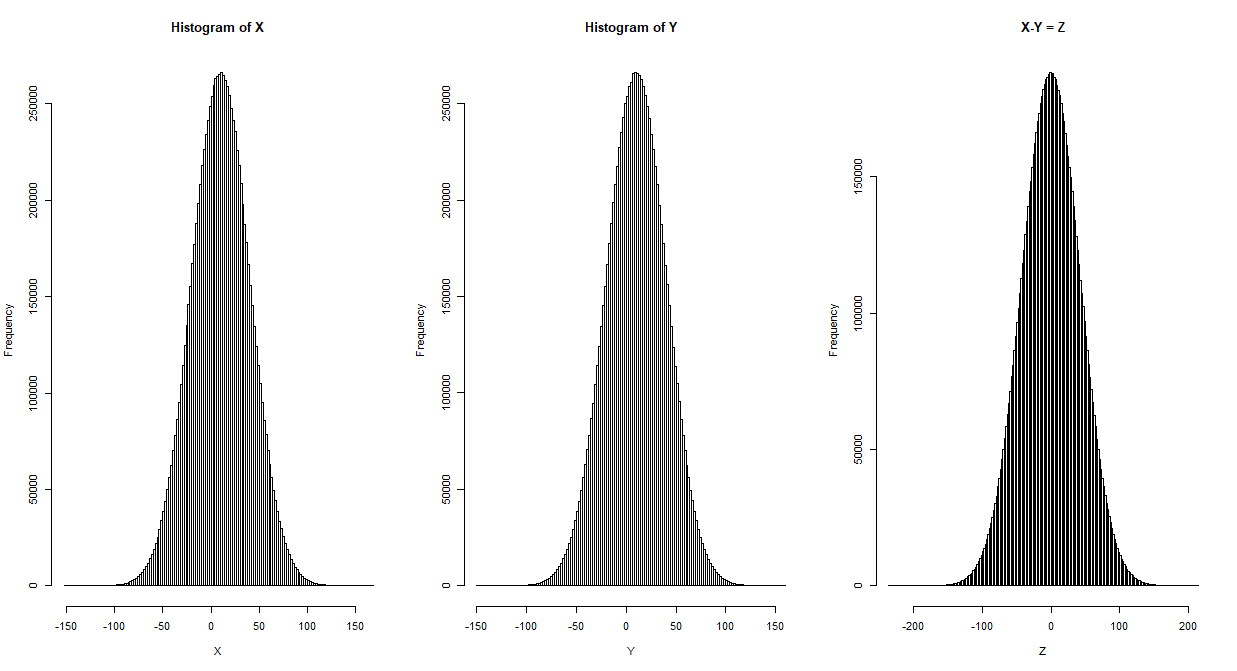
X <- rnorm(10000000,10,sqrt(900))
Y <- rnorm(10000000,10,sqrt(900))
par(mfrow=c(1,3))
hist(X,breaks=200)
hist(Y,breaks=200)
Z <- X-Y
hist(Z,main="X-Y = Z",breaks=200)
たしかにX-Yという値もX,Yと同じように正規分布していることが分かる。
さらに「分散」についても「ある性質」が成り立つ
X,Yという値の持つ分散の合計値が、X-Yの分散の値となる。という性質が成り立つ。
X \sim N(\mu_1, \sigma^2_1) \\\
Y \sim N(\mu_2, \sigma^2_2) \\\
X-Y \sim N(\mu_1 - \mu_2, \sigma^2_1 + \sigma^2_2)
mean((X-mean(X))^2) + mean((Y-mean(Y))^2)
[1] 1800.408
# 900+900に一致
X + Yという値の時は平均値が足し算になるだけで
X+Y \sim N(\mu_1 + \mu_2, \sigma^2_1 + \sigma^2_2)
のようになる。
標本だったら?
過去に標本平均に関する記事も書いたが、標本平均のばらつきというのは、標準偏差をサンプル数の平方根で補正した値となる。
X \sim N(\mu_1, \sigma^2_1) \\\
size=n \\\
sampleX \sim N(\bar{x}, \frac{\sigma^2_1}{n})
鉛筆の問題に戻って
以上の話から、もし工場Aと工場Bで平均的な長さが変わらないのならば、正規分布の再生性より、
X-Y \sim N(0, \frac{\sigma^2_1}{n} + \frac{\sigma^2_2}{m})
に従うはずである。
ただし、A工場からのサンプルサイズn、B工場からのサンプルサイズmとしている。
今回、仮にAから10個のサンプル、Bから20個のサンプルを抜き出したとする。
正規分布に従うデータの場合、標準偏差の2倍(正確には1.96倍)の値までにデータの95%が収容されていることが知られている。
もう少しかみ砕いで説明すると、「同じ検査を100回行ったときに95回はその範囲内の値になる」という範囲のことである。
この性質を使って、「偶然のばらつきとは言えない値」を「平均から95%の範囲よりも外れた位置にある値」と解釈しなおす。
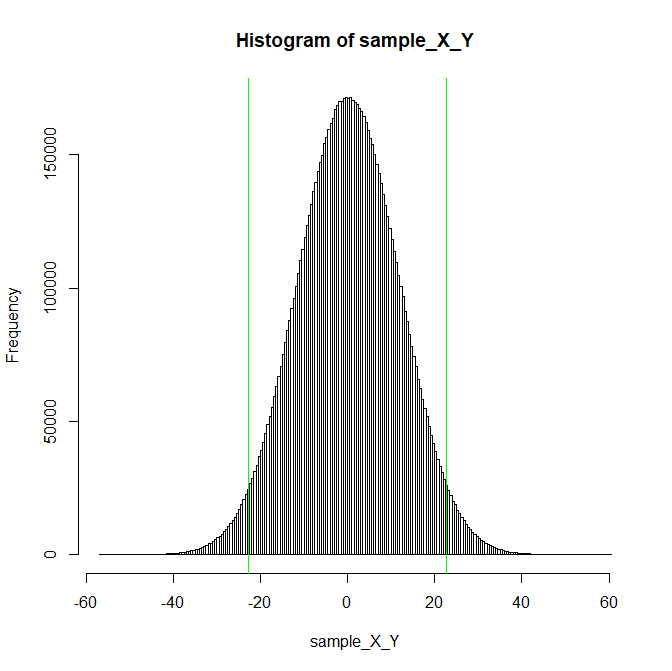
X-Yの図で、以下の緑色の線よりも平均値から遠いデータならば「偶然のばらつきとは言えない」と見なす。
sample_10_X <- rnorm(10000000,10,sqrt(900/10))
sample_20_Y <- rnorm(10000000,10,sqrt(900/20))
sample_X_Y <- sample_10_X - sample_20_Y
hist(sample_X_Y,breaks=200)
abline(v=1.96*sqrt(900/20 + 900/10),col="green")
abline(v=-1.96*sqrt(900/20 + 900/10),col="green")
900/20 + 900/10
[1] 135
mean((sample_10_X-mean(sample_10_X))^2) + mean((sample_20_Y-mean(sample_20_Y))^2)
[1] 135.0443
緑色の線の計算は
+1.96 * \sqrt{(900/20 + 900/10)} = 22.7 \\\
-1.96 * \sqrt{(900/20 + 900/10)} = -22.7
で求まる。
よって、今回の問題では22.7センチよりも小さい差であれば、「偶然そういうズレが生まれることもあるよね」と考えられる。
分散がなぜ合計値になるか分からない
問題解くだけなら以上の考え方で用が済んでいるのだが、
なぜ分散が
\sigma^2_1 + \sigma^2_2
となるのかがどうしても気になった。
ここから長い旅が始まった。
高校の数列から母関数まで説明
その前に期待値を振り返ります。
期待値とは、確率変数と確率密度関数の積の総和のことでした。
ピンとこない場合は高校の教科書のサイコロの目の期待値を参照してください。
E[X]= \sum{X*f(x)} = \int{X*f(x)} dx
Xの時の期待値だけでなく、$$X^2,X^3,X^4,.....$$
といった色々な時の期待値を計算したいとする。
(具体的にどういったときに使いたいのかは分散を求めたり尖度を求めたりするときに使う)
つまり、
\int{X*f(x)} dx, \int{X^2*f(x)} dx, \int{X^3*f(x)} dx,....
を求めたいということである。
このカタチを見ると、$$X^n$$
が変化している数列となっている(数列として扱えそうな気がする)。
ちなみに読み方はXのn乗と読み、これを計算することをべき乗(冪乗)するあるいは冪演算する(XかけるXかけるXかける.....)と呼ぶ。
数列の値をそれぞれ総和をとったものを級数と呼ぶのだった。
べき乗に関する級数を冪級数と呼ぶ。
\sum{X^0 + X^1 + X^2 + X^3 + X^4 +....}
冪級数に確率密度関数を掛けると、
\sum{X^0f(x) + X^1f(x) + X^2f(x) + X^3f(x) + X^4f(x) +....}
となる。
確率密度関数を係数と見なし、その係数は確率密度関数の数列であるとみなすと、
a_n = {f(x),f(x),f(x),...} \\\
X^n = {X^0 + X^1 + X^2 + X^3,...} \\\
\sum_{n=0}^{\infty}{a_nX^n}
として一般化できる。
この一般化したものを特に形式的冪級数 (formal power series)と呼ぶ。
数学では、このような係数に数列が入っている形式的冪級数のことを母関数と呼ぶ。
母関数にもいろいろあるが、詳しくはwikiを見てもらうとして、母関数の中でも
通常型母関数 (ordinary generating function)と言えば普通形式的冪級数の事を指す。
G(a_n;X) = \sum_{n=0}^{\infty}{a_nX^n}
母関数は上記のように数列を持ち、Xを変数として扱う関数G()のような形で表現される。
数列が確率密度関数である場合は確率母関数と呼ばれたりもする。
計算するとき
総和を計算するときに、上記は分割して計算しても値は等しくなるので、
\sum{X^0f(x)} + \sum{X^1f(x)} + \sum{X^2f(x)} + \sum{X^3f(x)} + \sum{X^4f(x)} +....
を計算してやればよい。もしも確率密度関数f(x)が離散値ならば上記で、連続値なら積分に変えればよい。
確率論でのモーメントという言葉について
物理、数学、いろいろなところで出てくる「モーメント」という言葉だが、ここでは確率論の「モーメント」について扱う。
**モーメント(積率)**とは、確率変数Xのべき乗に対する期待値のこと
つまりn乗のnが1ならば
Xの1乗の期待値
E[X] = \sum{Xf(x)}
もモーメントであり、nが2ならば
Xの2乗の期待値
E[X^2] = \sum{X^2f(x)}
もまたモーメントである。
このnは可変であり、それぞれのモーメントの事を、
n次モーメントと呼ぶ。
母関数とモーメントの関係
母関数(通常母関数=形式的べき級数)の計算
\sum{X^0f(x)} + \sum{X^1f(x)} + \sum{X^2f(x)} + \sum{X^3f(x)} + \sum{X^4f(x)} +....
n次モーメント
E[X^n] = \sum{X^nf(x)}
こうして並べてみると分かるが、母関数のnの時の要素の一つを取り出した値がn次モーメントになっていることが分かる。
しかし母関数とはすべての和を計算するような関数である。
この母関数に数学的なテクニックを加えると、n次のモーメントだけを取り出すことが出来るようになる。
そのテクニックというのはテイラー展開と呼ばれるもので、大学数学に登場するものである。
簡単に説明すると、関数があった時、その関数を単純な多項式に変形してくれるというものである。
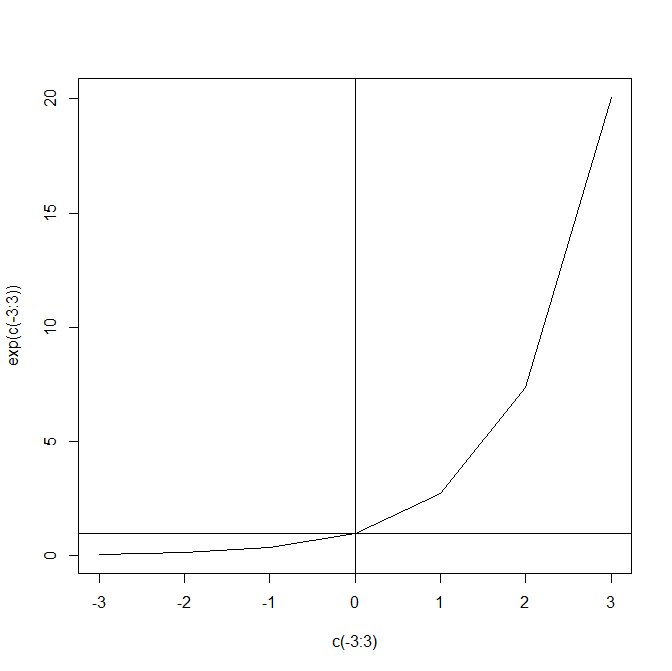
例として指数関数をテイラー展開してみる。
指数関数とは
e^x
のことであり、e=2.718....という値である。
図にすると
plot(c(-3:3),exp(c(-3:3)),type="l")
abline(v=0)
abline(h=1)
このような関数をしている。
e^x
をもっと人間が理解しやすいような形に変形できるのがテイラー展開であり、詳しい展開方法は今回説明しないが、具体的テイラー展開を行うと結果は
e^x = \frac{1}{0!}x^0 + \frac{1}{1!}x^1 + \frac{1}{2!}x^2 + \frac{1}{3!}x^3 + ....
というXに関する多項式に変換することができる。
この指数関数のテイラー展開の中にべき級数が隠れていることがわかってもらえると思う。
この指数関数のテーラー展開するとべき級数が現れる特性を使って、母関数から任意のn次モーメントを取り出そうと考えた頭のおかしい(賞賛)人が居たのだろう。
指数関数にもう一工夫してからテイラー展開を行うと、
e^{tx} = \frac{t^0}{0!}x^0 + \frac{t^1}{1!}x^1 + \frac{t^2}{2!}x^2 + \frac{t^3}{3!}x^3 + ....
となる。
このひと工夫した指数関数を使って期待値を考える。
E[e^{tx}] \\\
= \sum{e^{tx} f(x)} \\\
= \sum{\frac{t^0}{0!}x^0f(x) + \frac{t^1}{1!}x^1f(x) + \frac{t^2}{2!}x^2f(x) + \frac{t^3}{3!}x^3f(x) + .... }
この式を、tに関する関数として考え、tで一回微分する。
M_x(t) = = \sum{\frac{t^0}{0!}x^0f(x) + \frac{t^1}{1!}x^1f(x) + \frac{t^2}{2!}x^2f(x) + \frac{t^3}{3!}x^3f(x) + .... } \\\
M'_x(t) = = \sum{0 + \frac{1}{1!}x^1f(x) + \frac{2t}{2!}x^2f(x) + \frac{3t^2}{3!}x^3f(x) + .... }
ここで面白いことに、t=0を代入してみると、
M'_x(t=0) = \sum{\frac{1}{1!}x^1f(x)} = \sum{xf(x)}
なんと1次のモーメント(f(x)でのXの時の期待値)が残った。
ちなみにtについて2回微分し、t=0を代入すると2次のモーメントだけがのこるので気になったら試してみてほしい。
このような
「モーメント(積率)」をうまく取り出せるような「母関数」という性質から、「モーメント(積率)母関数」
と名前がついている。
正規分布でのモーメント母関数について
今ここまでf(x)を特に指定せず、期待値(n次モーメント)を求める過程を一般化してきたが、具体的にf(x)を正規分布として仮定するとどうなるのだろうか?
正規分布とは
f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp{\Biggl(-\frac{(x-\mu)^2}{2\sigma^2}\Biggr)}
のような数式であった。
E[e^{tx}]
= \sum{e^{tx} f(x)} \\\
であり、f(x)に正規分布を代入してやると、
\sum{\exp{\Biggl(tx\Biggr)} \frac{1}{\sqrt{2\pi\sigma^2}}\exp{\Biggl(-\frac{(x-\mu)^2}{2\sigma^2}\Biggr)}}
指数の性質より、eのべき乗同士の掛け算は、指数を足し算したものでeのべき乗を計算してやることに等しいので
= \sum{\frac{1}{\sqrt{2\pi\sigma^2}}\exp{\Biggl(-\frac{(x-\mu)^2}{2\sigma^2} + tx\Biggr)}}
eの指数の中身を展開したり、分母をくくり出して整理すると
= \sum{\frac{1}{\sqrt{2\pi\sigma^2}}
\exp{\Biggl(-\frac{1}{2\sigma^2}(x^2 - 2\mu x+\mu^2 + 2\sigma^2 tx)\Biggr)}}
証明のための天下り的に指数の中に
\mu t + \frac{\sigma^2 t^2}{2}
を無理やり入れる。ここで一旦指数の中だけを考える。
\exp{\Biggl(
-\frac{1}{2\sigma^2}(x^2 - 2\mu x+\mu^2 + 2\sigma^2 tx) +(\mu t + \frac{\sigma^2 t^2}{2})-(\mu t + \frac{\sigma^2 t^2}{2})
\Biggr)} \\\
この式から
\exp(\mu t + \frac{\sigma^2 t^2}{2})
をくくり出す。
\exp{\Biggl(
-\frac{1}{2\sigma^2}(x^2 - 2\mu x+\mu^2 + 2\sigma^2 tx) +(\mu t + \frac{\sigma^2 t^2}{2})-(\mu t + \frac{\sigma^2 t^2}{2})
\Biggr)} \\\
= \exp{\Biggl(
\mu t + \frac{\sigma^2 t^2}{2}
\Biggr)}
\exp{\Biggl(
-\frac{1}{2\sigma^2}(x^2 - 2\mu x+\mu^2 + 2\sigma^2 tx) -(\mu t + \frac{\sigma^2 t^2}{2})
\Biggr)} \\\
右側の指数は平方完成できる。
\exp{\Biggl(
\mu t + \frac{\sigma^2 t^2}{2}
\Biggr)}
\exp{\Biggl(
-\frac{(x-(\mu+\sigma^2 t))^2}{2\sigma^2}
\Biggr)} \\\
指数の中に注目するのはここまで。
くくり出した項はxを含まない定数のため、以下のように変形できる。
\exp{\Biggl(
\mu t + \frac{\sigma^2 t^2}{2}
\Biggr)}
\sum{\frac{1}{\sqrt{2\pi\sigma^2}}
\exp{\Biggl(
-\frac{(x-(\mu+\sigma^2 t))^2}{2\sigma^2}
\Biggr)}} \\\
ここで
\mu + \sigma^2 t = A
とおくと、
\exp{\Biggl(
\mu t + \frac{\sigma^2 t^2}{2}
\Biggr)}
\sum{\frac{1}{\sqrt{2\pi\sigma^2}}
\exp{\Biggl(
-\frac{(x-A)^2}{2\sigma^2}
\Biggr)}} \\\
ここで総和記号の項を見てみると、平均A標準偏差σの正規分布になっていることがわかる。
総和記号は今回連続値の確率密度関数を扱っているので積分の記号であらわすのが正しい。
修正します。
\exp{\Biggl(
\mu t + \frac{\sigma^2 t^2}{2}
\Biggr)}
\int_{-\infty}^{\infty}{\frac{1}{\sqrt{2\pi\sigma^2}}
\exp{\Biggl(
-\frac{(x-A)^2}{2\sigma^2}
\Biggr)}} \\\
正規分布の確率密度関数を負の無限から正の無限までの積分というのは、
確率の総和の意味なので、合計1である。
よって残るのは前の項だけである。
長くなったが、
M_x(t) \\\
= E[e^{tx}] \\\
= \sum{e^{tx} f(x)} \\\
=\exp{\Biggl(
\mu t + \frac{\sigma^2 t^2}{2}
\Biggr)} \\\
となり、この関数はtについての関数である。
この式をテイラー展開してやると、正規分布のXの時の期待値や、X^2の期待値などが計算できるようになる。
ようやくここで最初の問題での疑問に戻る
XとYという正規分布に従う確率変数があり、
X+YやX-Yも正規分布に従うという再生性を確認し終えて、
「これらの計算値のばらつきは(Xの分散+Yの分散)に等しくなる。」
という性質を納得するために長い道のりを歩んできた。
ここで、XとYは独立な正規分布に従う値であるという前提がある。
独立とは、Xの値を観測するとYの値が変化するとか、その逆の現象などもない、という性質のこと。
X-Yの期待値に関する積率母関数
E[e^{t(X-Y)}]
は、X,Yが独立であるので指数の性質より、分割して計算しても問題がない
E[e^{t(X-Y)}] = E[e^{tX}]E[e^{tY}]
先ほどの正規分布の期待値に関する積率母関数の変換より、
E[e^{tX}]E[e^{tY}] \\\
=\exp{\Biggl(
\mu_X t + \frac{\sigma_X^2 t^2}{2}
\Biggr)} \exp{\Biggl(
\mu_Y t + \frac{\sigma_Y^2 t^2}{2}
\Biggr)}
\\\
と変形でき、指数を整理することで、
\exp{\Biggl(
(\mu_X-\mu_Y) t + \frac{(\sigma_X^2+\sigma_Y^2) t^2}{2}
\Biggr)}
という式が導出できた。
よって、X+Yの積率母関数の変形から、X-Yは
X-Y \sim N(\mu_X-\mu_Y,\sigma_X^2+\sigma_Y^2)
に従うことが証明できた。
おわり
ただ一問の差の検定から、ずいぶん深いところまで掘り進めることになってしまった。