勉強した内容の備忘録
今回の記事では、画像によって使用している乱数データが異なるため、すべてのデータで図形が一致していない場合があります
データの作成
対応のあるデータと仮定する
m10<-rnorm(1000,10,1)
m25<-rnorm(1000,25,3)
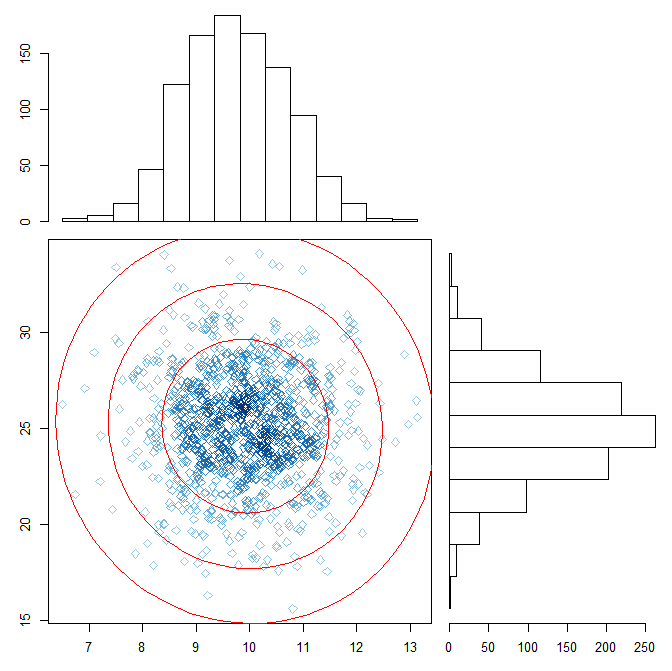
どんなデータかplotしてみる。
# http://cse.naro.affrc.go.jp/takezawa/r-tips/r/55.html
# 図を描く部分をlayoutで指定してやる
# 2×2のプロットエリアをつくる。
# 左上に図1,左下に図2,右下に図3が入力される
layout(matrix(c(1,0,2,3),2,2,byrow=TRUE),c(2,1),c(1,2),TRUE)
m_data=data.frame(m10=m10,m25=m25)
# 図1
par(mar=c(0,3,1,1))#図の間の隙間を狭くしてやる
hist_m10_data <- hist(m10,right=FALSE,plot=FALSE)
barplot(hist_m10_data$counts,space=0,col=0)
# 図2
par(mar=c(3,3,1,1))
plot(m_data,col=densCols(m10,m25),pch=5,cex=1)
library(ellipse)#楕円を3σ区間まで書き込む
var_m10_m25 <- var(m_data)
mean_m10 <- mean(m_data$m10)
mean_m25 <- mean(m_data$m25)
lines(ellipse(var_m10_m25, level=0.6827, centre=c(mean_m10,mean_m25), add=T),lwd=1,lty=1,col=2)
lines(ellipse(var_m10_m25, level=0.9545, centre=c(mean_m10,mean_m25), add=T),lwd=1,lty=1,col=2)
lines(ellipse(var_m10_m25, level=0.9973, centre=c(mean_m10,mean_m25), add=T),lwd=1,lty=1,col=2)
# 図3
par(mar=c(3,0,1,1))
hist_m25_data <- hist(m25,right=FALSE,plot=FALSE)
barplot(hist_m25_data$counts,space=0,col=0,horiz=T)
plotとhistでデータの密度をなんとなく確認できた。
密度推定
# https://qiita.com/qooa/items/93a5410be54af9031a27
# http://cse.naro.affrc.go.jp/takezawa/r-tips/r/61.html
MASSから二次元カーネル密度推定を行うkde2dを呼び出す
library("MASS")
dens <- kde2d(m10,m25,n=50)
# nで次元を指定
# dim(dens$z)
# [1] 50,50
この計算された密度を確認してみる。
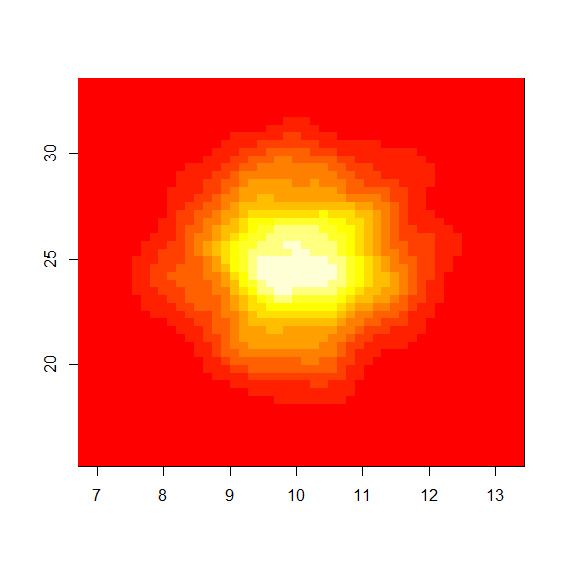
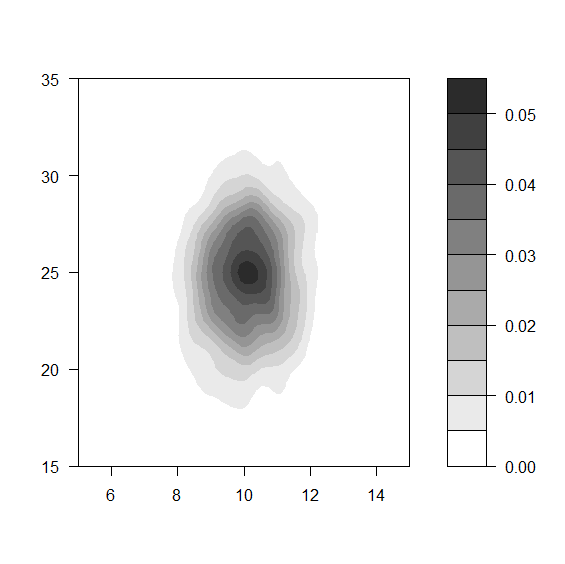
image(dens)
imgで表示すると、画像で密度の高い部分が確認できる。
もう少しわかりやすい図示
library(epade)
par(mfrow=c(1,1))
par(mar=c(5,1,5,1))
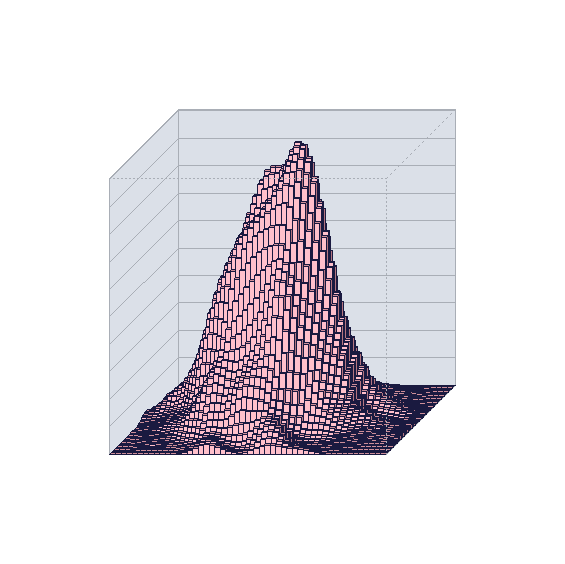
bar3d.ade(dens$z,xw=5,zw=0.1,axes=FALSE,col="pink",wall=3,alpha=1)
3Dで確認できた。
等高線でも確認してみる
# データを切りのいい段階で分けるpretty
# 密度の区切りを10個の区切りで切って、色を変えることで密度の高い部分をわかりやすくする
lev <- pretty(range(dens$z),10)
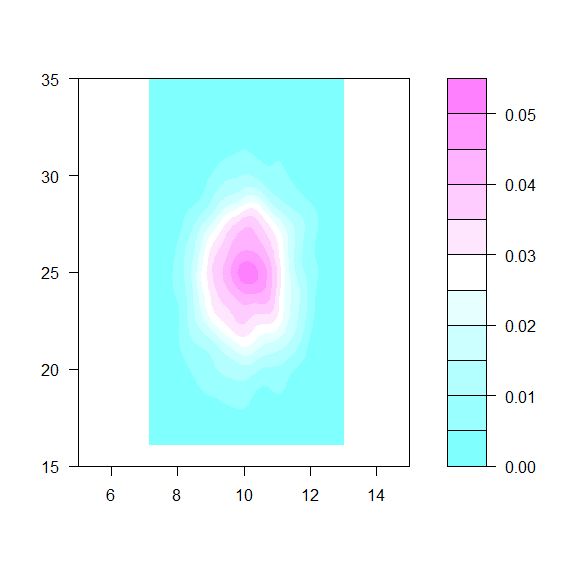
filled.contour(dens,levels=lev,xlim=c(5,15),ylim=c(15,35))
filled.contour(dens, levels=lev,col=gray((length(lev):1)/length(lev)),xlim=c(5,15),ylim=c(15,35))
もっと詳細に等高線を使って確認する。
95%について書いてみる
library(spam)
library(maps)
library(fields)
# 引数に指定したもののすべての組み合わせをつくるexpand.grid
# http://cse.naro.affrc.go.jp/takezawa/r-tips/r/46.html
grid <- expand.grid(dens$x,dens$y)
grid2 <- cbind(grid, data.frame(as.vector(dens$z)))
# https://www.rdocumentation.org/packages/fields/versions/9.6/topics/Tps
# http://www.okadajp.org/RWiki/?%E7%9F%A5%E3%81%A3%E3%81%A6%E3%81%84%E3%82%8B%E3%81%A8%E3%81%84%E3%81%A4%E3%81%8B%E5%BD%B9%E3%81%AB%E7%AB%8B%E3%81%A4%28%3F%29%E9%96%A2%E6%95%B0%E9%81%94
# http://www.math.keio.ac.jp/~kei/GDS/2nd/spline.html
# thin plate spline法で計算
model <- Tps(grid2[,1:2],grid2[,3])
# 作成したmodelをpredictに当てはめて予想値を入れる
m_data<-data.frame(m10=m10,m25=m25)
m_data$dens <- predict(model, m_data[,1:2])
# http://www.okadajp.org/RWiki/?%E3%82%B0%E3%83%A9%E3%83%95%E3%82%A3%E3%83%83%E3%82%AF%E3%82%B9%E5%8F%82%E8%80%83%E5%AE%9F%E4%BE%8B%E9%9B%86%EF%BC%9A%E3%82%A4%E3%83%A1%E3%83%BC%E3%82%B8%E5%9B%B3
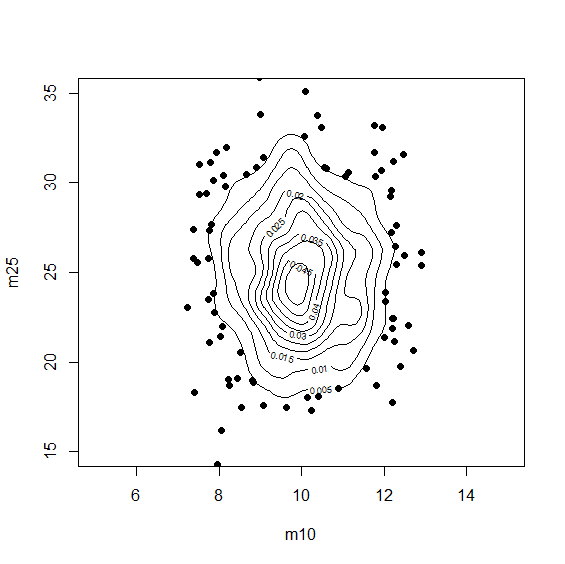
# データ中で0.005を満たさないものをplotする
plot(m_data[m_data$dens<0.005,1:2],xlim=c(5,15),ylim=c(15,35),pch=16)
contour(dens,add=T)
nrow(m_data[m_data$dens<0.005,1:2])
で確認してみると、1000個中85個のデータが外れていた。
測定データなどでは、これらを外れ値と扱うのかもしれない。
ggplotを使って95%を描く場合
library(ggplot2)
# https://stackoverflow.com/questions/23437000/how-to-plot-a-contour-line-showing-where-95-of-values-fall-within-in-r-and-in
getLevel <- function(x,y,prob=0.95) {
kk <- dens
dx <- diff(dens$x[1:2])
dy <- diff(dens$y[1:2])
sz <- sort(dens$z)
c1 <- cumsum(sz) * dx * dy
approx(c1, sz, xout = 1 - prob)$y
}
AA<-data.frame(m10=m10,m25=m25)
L95 <- getLevel(AA$m10,AA$m25)
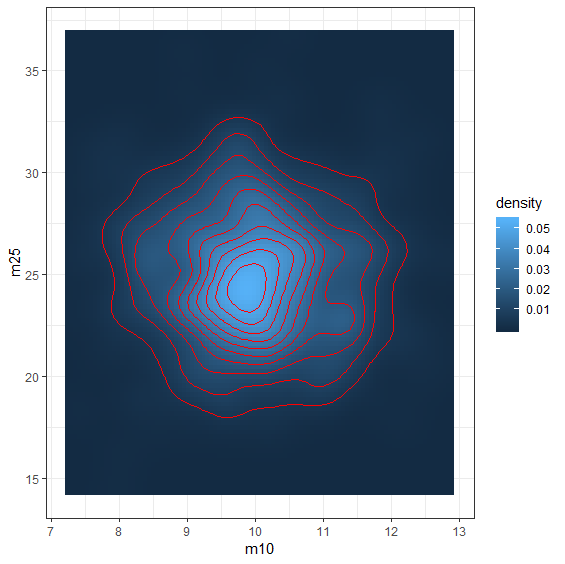
ggplot(AA,aes(m10,m25)) +
stat_density2d(geom="tile", aes(fill = ..density..), contour = FALSE)+
stat_density2d(colour="red",breaks=L95)
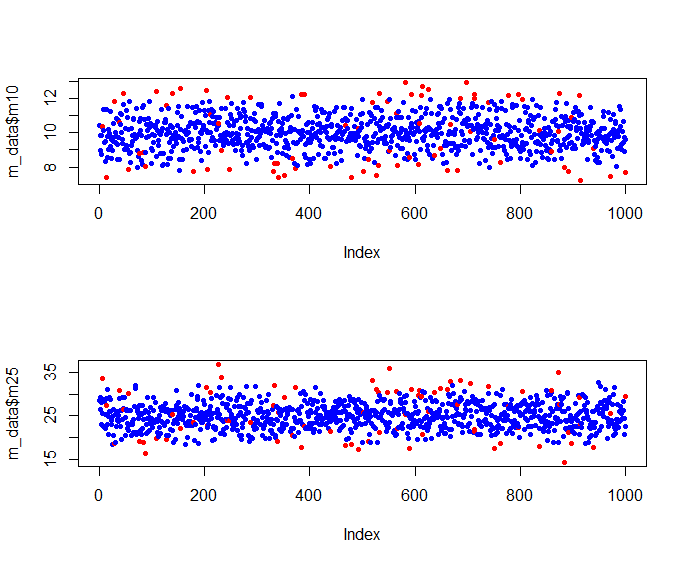
95%を外れていたものを赤色にしてplot
par(mfrow=c(2,1))
plot(m_data$m10,col=c("blue","red")[unclass(m_data$result+1)],pch=20)
plot(m_data$m25,col=c("blue","red")[unclass(m_data$result+1)],pch=20)