前回の単回帰の流れから重回帰もまとめてしまう。
重回帰
重回帰ではニューヨークの大気データの「airquality」を使います。
ニューヨークの大気データ154日
オゾン量、太陽放射強度、風、気温のデータが入っています。
たとえば体に降り注ぐオゾンの量は簡単に測定できないものとして、
太陽の強さと風と気温という身近な指標から予測するモデルを作りたいと思います。
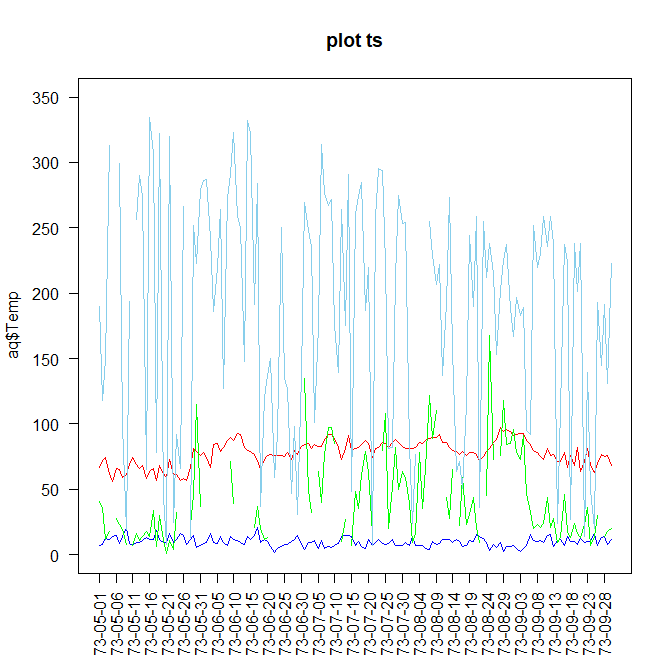
時系列に並んでいるデータなので、時期によって影響は無いのかも含めてとりあえずplotです。
aq=airquality
times=as.POSIXct(paste0("1973-",airquality$Month,"-",airquality$Day),format="%Y-%m-%d")
aq$time=times
y_limit<-c(0,350)
matplot(aq$time, aq$Temp,
type="n", lty=0, xaxt="n", xlab="",
las=1, ylim=y_limit, main="plot ts")
matpoints(aq$time, aq$Temp, type="l", lty=1,col="red")
matpoints(aq$time, aq$Wind, type="l", lty=1,col="blue")
matpoints(aq$time, aq$Ozone, type="l", lty=1,col="green")
matpoints(aq$time, aq$Solar.R, type="l", lty=1,col="skyblue")
axis.POSIXct(side=1,
at=seq(as.POSIXct(aq$time[1]),
as.POSIXct(aq$time[153]),
"5 day"), las=2, format="%y-%m-%d")
ところどころデータが欠損してます。
summary(aq)
Ozone Solar.R Wind Temp
Min. : 1.00 Min. : 7.0 Min. : 1.700 Min. :56.00
1st Qu.: 18.00 1st Qu.:115.8 1st Qu.: 7.400 1st Qu.:72.00
Median : 31.50 Median :205.0 Median : 9.700 Median :79.00
Mean : 42.13 Mean :185.9 Mean : 9.958 Mean :77.88
3rd Qu.: 63.25 3rd Qu.:258.8 3rd Qu.:11.500 3rd Qu.:85.00
Max. :168.00 Max. :334.0 Max. :20.700 Max. :97.00
NA's :37 NA's :7
Month Day time
Min. :5.000 Min. : 1.0 Min. :1973-05-01
1st Qu.:6.000 1st Qu.: 8.0 1st Qu.:1973-06-08
Median :7.000 Median :16.0 Median :1973-07-16
Mean :6.993 Mean :15.8 Mean :1973-07-16
3rd Qu.:8.000 3rd Qu.:23.0 3rd Qu.:1973-08-23
Max. :9.000 Max. :31.0 Max. :1973-09-30
OzoneとSolar.Rが欠損値を含んでいるようです。
NAのある行を単純に削除するなら
aq_del_na=na.omit(aq)
ですがplotしてみたら波形になっていて、前後の値と関係していそうなので、
前後の値の合計の平均を使って埋めたいと思います。
より正確に埋めたかったらSVMとか使って欠損値の推測とかもするんでしょうか。
library(zoo)
aq$Ozone=na.approx(aq$Ozone)
aq$Solar.R=na.approx(aq$Solar.R)
Ozoneの上から五行目を見てみるとNAが23になっています
Ozoneの4行目(18)と6行目(28)を足した平均が23なのでできていそうです。
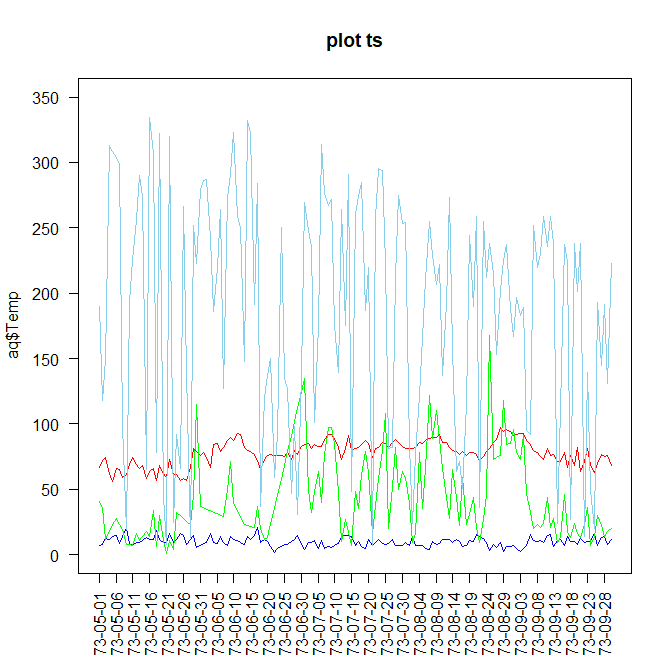
欠損値を埋めた状態でplotしてみます。
一見して埋めた値におかしなところはなさそうです。
データの列に月や日が入っているので、単純に変数だけにします。
aq_relation_plot=data.frame(Ozone=aq$Ozone,Solar=aq$Solar.R,Wind=aq$Wind,Temp=aq$Temp)
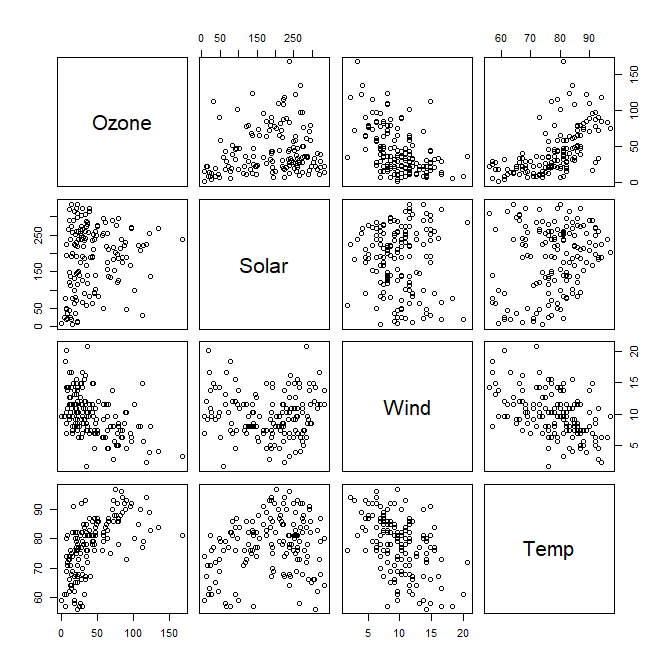
関係を各変数でplotして比較してみたら
・windとtempで負の相関
・windとozoneに微妙に負の相関
・tempとozoneに正の相関
がありそうでしょうか?
cor(aq_relation_plot)
Ozone Solar Wind Temp
Ozone 1.0000000 0.15947312 -0.50753419 0.6016359
Solar 0.1594731 1.00000000 -0.02927963 0.2296967
Wind -0.5075342 -0.02927963 1.00000000 -0.4579879
Temp 0.6016359 0.22969669 -0.45798788 1.0000000
実際に相関係数を確認してみます
「ozoneとsolar」「windとsolar」の間に相関はなさそうです
実際に重回帰してモデルにしてみます。
model=lm(Ozone~Solar+Wind+Temp,data=aq_relation_plot)
summary(model)
Call:
lm(formula = Ozone ~ Solar + Wind + Temp, data = aq_relation_plot)
Residuals:
Min 1Q Median 3Q Max
-39.651 -15.622 -4.981 12.422 101.411
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -52.16596 21.90933 -2.381 0.0185 *
Solar 0.01654 0.02272 0.728 0.4678
Wind -2.69669 0.63085 -4.275 3.40e-05 ***
Temp 1.53072 0.24115 6.348 2.49e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 24.26 on 149 degrees of freedom
Multiple R-squared: 0.4321, Adjusted R-squared: 0.4207
F-statistic: 37.79 on 3 and 149 DF, p-value: < 2.2e-16
43%くらいデータを説明できていそうなモデルが出来ました。
結果を見てみると、
ozone = solar0.01654 + wind(-2.69669) + 1.53072*temp -52.16596
というモデルが出てきました。
検定結果を見るとsolarはほとんど影響していなさそうなので、
ozone = wind*(-2.69669) + 1.53072*temp -52.16596
という式で十分に説明が出来そうです。
これにて終わり!・・・・・でいいのか?
そこまで重要でない予測ならいいですが、
せっかく多変量なのでモデル選択やモデルの検証も行っていきます。
分散拡大係数(variance inflation factor : VIF)
説明変数の相関係数行列の対角要素。
パッケージcarのVIFの関数を使うと多重共線性(multicollinearity)の程度が計算できるようです。
10よりも大きいと変数間の相関が大きいという事になり、そのような変数はモデルから取り除くのが良い。
多変量の重回帰ではデータを説明する変数が多いほどモデルの当てはまりがよくなる。
説明変数間に強い相関のあるデータが混ざっていると検定結果が有意になったり、実はモデルがデータを全く説明できていないのに、決定係数が見かけ上だけ大きな値になってしまう
などが起こるようです。
もし大きければ変数を一部外したり、取り除くようです。
library(car)
print(vif(model))
Solar Wind Temp
1.063891 1.275246 1.345122
モデルの説明変数に強い相関を持つデータはありませんでした。
モデルの最適化 AIC(Akaike's Information Criterion)
モデルの最適さを表すと言えばこのAICが出てきます。
AICはモデルを比較して理想を探してくれる関数です。
Rでは比較して一番いい物を見つけてくれるstep関数があるので使いましょう。
best_model=step(model)
Start: AIC=979.78
Ozone ~ Solar + Wind + Temp
Df Sum of Sq RSS AIC
- Solar 1 311.9 88035 978.32
<none> 87723 979.78
- Wind 1 10758.1 98481 995.48
- Temp 1 23721.2 111444 1014.40
Step: AIC=978.32
Ozone ~ Wind + Temp
Df Sum of Sq RSS AIC
<none> 88035 978.32
- Wind 1 10520 98555 993.59
- Temp 1 26642 114677 1016.77
モデルとしてはsolarを外したものが最もAICを下げてくれていいモデルであるようですね。
さっきの上で述べた検定とも一致します。
summary(best_model)
Call:
lm(formula = Ozone ~ Wind + Temp, data = aq_relation_plot)
Residuals:
Min 1Q Median 3Q Max
-40.563 -15.252 -4.606 12.607 102.384
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -52.8013 21.8576 -2.416 0.0169 *
Wind -2.6564 0.6274 -4.234 3.99e-05 ***
Temp 1.5734 0.2335 6.738 3.23e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 24.23 on 150 degrees of freedom
Multiple R-squared: 0.4301, Adjusted R-squared: 0.4225
F-statistic: 56.6 on 2 and 150 DF, p-value: < 2.2e-16
モデルの説明具合は43%くらいのままですね。
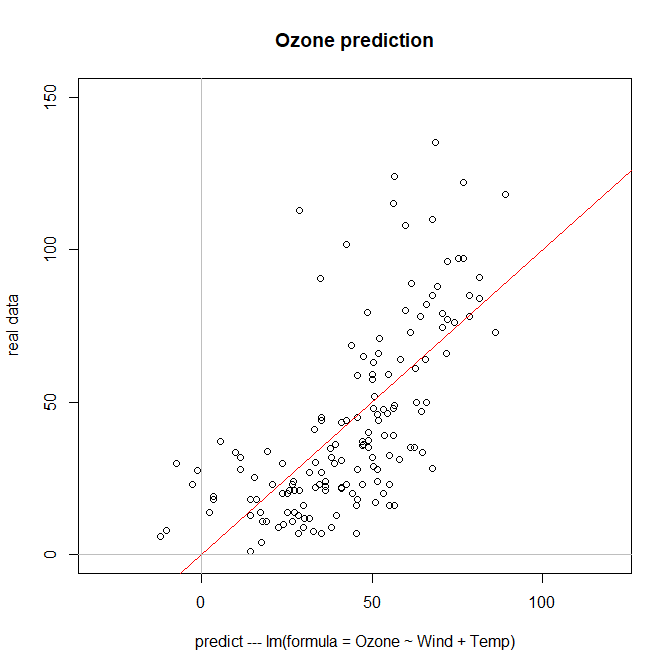
今回得られた予測式を使って得られる予測値と、実際の値を並べてみます
plot(x=best_model$fitted.value, y=aq$Ozone,
main="Ozone prediction",
xlab="predict --- lm(formula = Ozone ~ Wind + Temp)",
ylab="real data",
xlim=c(-30, 120), ylim=c(0,150))
abline(0, 1, col="red")
abline(h=0, v=0, col="gray")
予測値は風の負の符号の影響を受けてオゾンがマイナスになってしまっている箇所がありますが、概ね予測式が出来ていそうです。
以上
今後は
リッジやPLS回帰などもまとめていきたいと思います。