せっかく本読んで実験したのでタグチメソッドの備忘録
タグチメソッドのパラメーター設計とは
世の中にシステムはいろいろある。
プリンターは使用時の温度や湿度に関わりなく綺麗に静かに印刷することが求められるし、
エンジンは高い耐久と燃費効率や排気ガス規制の中で求められる性能を出さなければならないし、
蛇口は回転角によって一定の水を出す必要があり、
乾電池は求められる定格の電圧を出す必要があり、
工場は人員や機械を適切に配置して従業員の生産性や製品の生産量を上げなければならない。
パラメーター設計はこのような様々なシステムを設計する際に使える。
品質や現状改善というよりも、新規設計の向きが強い。
実験計画法で見る直交表を使い入力(信号)・出力からなるシステムの設計をする手法である。
設計条件を「因子(パラメーター)」と呼び、因子の検討対象を「水準」と呼ぶ
因子は設計したい物の**出力(性能・機能)**に対して影響を与えることが想像できる
因子ごとに与える影響の大きさは違うだろう。
さらには因子同士の交互作用や、完成後の使用環境によって出力が不安定になることも考えられる。
そこで、
・因子の効果を調べる
・ノイズに強い因子の組み合わせを調べる
といった気持ちで実験を行う。
実験室で完璧に管理された状態で評価しても、実用に耐えないという考えから、強制的にノイズを発生させる。
「ノイズに強い」という点からロバスト設計とも呼ばれる。
因子と水準の例
- 対象システム「ゴム動力の飛行機」
- 出力「飛行距離」
- 入力「ゴムの捻じり回数」
- 因子「羽の幅・長さ・角度・機体の素材・ゴムの素材・劣化・プロペラの長さ・幅・重さ・枚数、などなど・・・」
- 水準:因子を羽の長さとしたなら「6,8,10 cm」が「水準1,2,3」となる
- ノイズ「向かい風・初速・羽の密度、などなど・・・」
対象システムや出力、入力は設計したい物であるので既知。
因子は関係者で集まりブレストを行うか、故障の木解析などで対策すべき点を洗い出す。
**"適切な因子"**を選ぶのは難しい。
ノイズは「使用時に発生する、設計として管理することができない」もの。
ノイズも因子と考え「誤差因子」と呼ばれる。
パラメーター設計の特徴
- 因子が出力に影響をあまり与えないことがわかれば、その因子はコストを優先したりできる
- 強制的にノイズを発生させることでノイズに対する耐性がわかる
- 結果の解釈が体系化されており、技術者に検定等を要求しない手法として考えられた
- (指標の解釈は難しいが、数字だけ見て判断できるように考えられている)
- 交互作用は調べられない(ダミー法等で検出する)
- 入力と出力の関係性を事前に理解している必要がある
- 実験回数が少なくて済む(タグチメソッドの本心は実験段階で**"早く失敗を起こす事"**)
パラメーター設計の前に実験計画法の話
実験計画法とR.A.フィッシャー
英国の統計学者ロナルド.A.フィッシャーは推測統計学の基礎を作り上げた人物であり、頻度論者の中でも特に有名な人物。
頻度論者フィッシャーやネイマンはベイズとバチバチに喧嘩していた話も有名。
最尤法や分散分析を考えだし、実験計画法も彼の研究によって生まれた。
1925年 Design of Experiment として実験計画法を発表する。
これはフィッシャーがロゼムスタッド農事試験場にて麦の品種改良を研究していた時、「(成長に影響を与える)因子の効果を効率よく少数の実験(サンプル)で評価したい」という目的から生まれた方法である。
また、今までの「経験的」な意見ではなく、誤差・検定・有意を使った意思決定を行うという目的もあった。
実験内容としては「因子をいくつかの段階(水準)に分けて実験し、因子の変化と出力の変化の関係を知るための手法」であった。
考えられることを実験で証明する「検証実験」というよりも、わからない部分実験で確かめる「発見的実験」に分類される。
フィッシャーの三原則
実験計画法では
1.局所管理
2.繰り返し
3.ランダム化
の三原則が思想として組み込まれている。
・実験環境や外部からの影響によってばらつきが発生しては実験効果が正確に測定できないため、実験は誤差を最小とするため小さく管理できる環境で行う。(局所管理)
・因子の効果を測るために繰り返し実験を行う(繰り返し)
・実験しやすいからといって実験順序に恣意性を持たせることは誤差の偏りにつながるのでランダムに行う事(ランダム化)
また、人の操作による作業は極力削減し、結果に誤差を含ませないように注意する。
1因子3水準の場合(一元配置)
1つの因子について、複数の水準を実験することを一元配置実験と呼ぶ
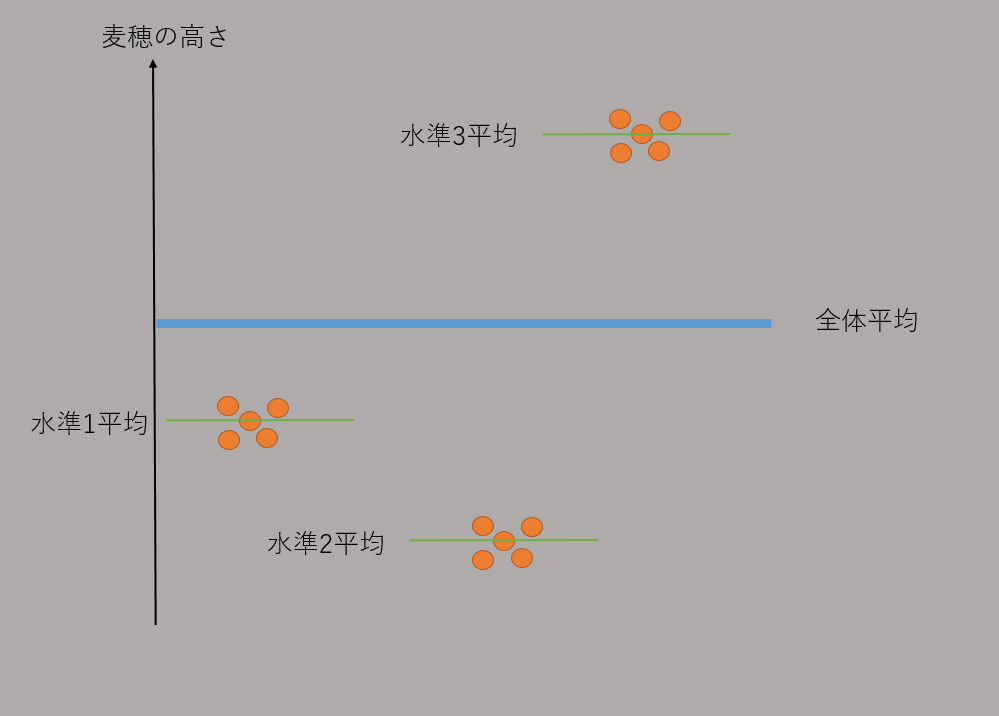
因子(肥料)の水準(1,2,3)を与えた時の麦穂の高さyを平均値の記号μを使って(μ1,μ2,μ3)と表す。
実験者であれば経験があると思うが、水準を合わせたからと言ってμ1,μ2,μ3の値がピッタリ出ることはまずない。
原材料に不純物が混ざっていたり、湿気で不活性になっていた場合には成長に影響が出るのは当然と思う。特に不活性になりやすい水準があっても不思議ではない。
水準の誤差を考えると以下のようになる。
y_{1},y_{2},y_{3}=\mu_{1}+\epsilon_{水準1},\mu_{2}+\epsilon_{水準2},\mu_{3}+\epsilon_{水準3}
さらに繰り返し実験として別のサンプルを採取するのでサンプルごとの誤差も考える必要がある。サンプルの番号をjとすると
y_{1j},y_{2j},y_{3j}=\mu_{1}+\epsilon_{水準1,j},\mu_{2}+\epsilon_{水準2,j},\mu_{3}+\epsilon_{水準3,j}
と表される。
このデータから「全体の平均(一般平均や総平均と呼ぶ)」と「各水準の平均」が求まり、どの水準が特に効果があったのかを確認することができる。
図を確認してもらうとわかるが、まさに分散分析の考え方である。
三元配置とL4直交表
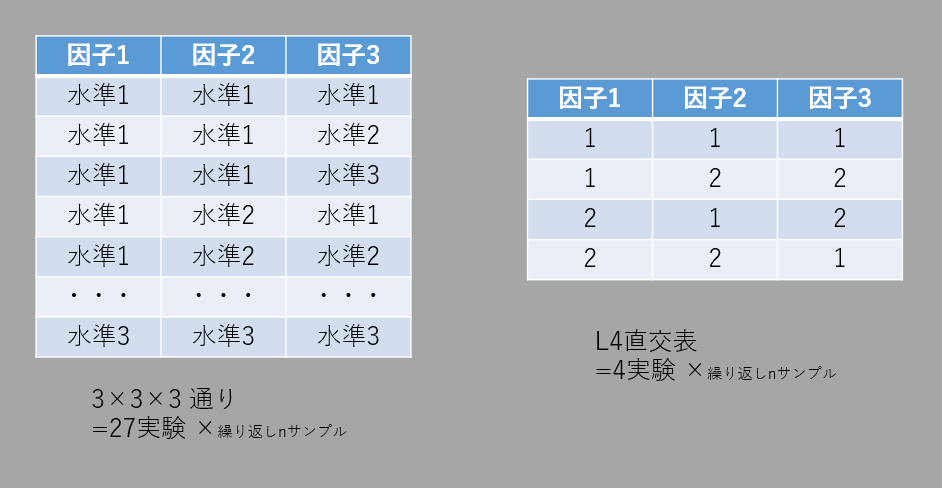
もし3因子3水準であったら?
すべてのパターンを実験するのには3×3×3通りの実験が必要となる。
さらに繰り返していくつかサンプルを採取するとなるとサンプル数だけ実験を増やす必要が発生する(一回の実験で複数サンプルできる場合を除く)。
そこで数学者たちは、
・因子1と因子2の各水準が網羅的に実験できる
・因子2と因子3が網羅的に実験できる
・因子1と因子3が網羅的に実験できる
という見方をすることで実験回数を減らすことを考えた。
こうすることで4回の実験で済むようになったのである。
これをL4直交表と呼ぶ
L18直交表と外側直交表(誤差因子)
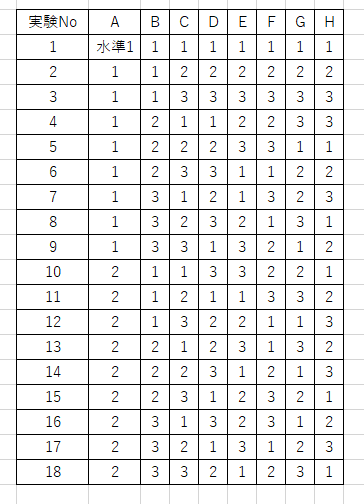
パラメーター設計で登場するL18直交表は
・2水準の因子が1つ
・3水準の因子を7つ
を組み合わせられる手法
合計で18回の実験を行う。
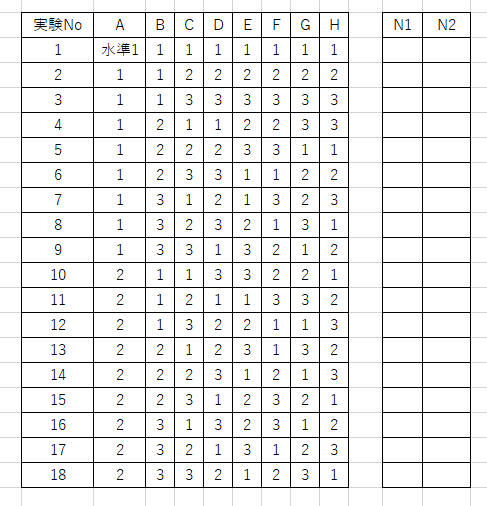
誤差因子の影響を各実験に対して観測するために外側直交表として組み合わせる方法もある
誤差因子は
出力が変わらない(N0),出力を小さくする(N1),出力を大きくする(N2)
を外側直交表に配置するが、N0は省略されることが多い
因子と水準を直交表にわりふることをわりあてと呼ぶ。
実験計画法では恣意的な実験の順序を決めることによって誤差が発生すると考え、
実験順のランダム性を重視したが、
パラメーター設計では、やりやすい実験順で効率よく設計開発することが推奨されている。
ノイズを強制的に発生させる、水準を動かす、ことで順序による小さいノイズを考えないでおく。
(このあたりはフィッシャー的な実験計画法との論争になっていたらしい。)
パラメーター設計の種類
入出力の**理想機能(関係)**の種類によって計算方法が異なる
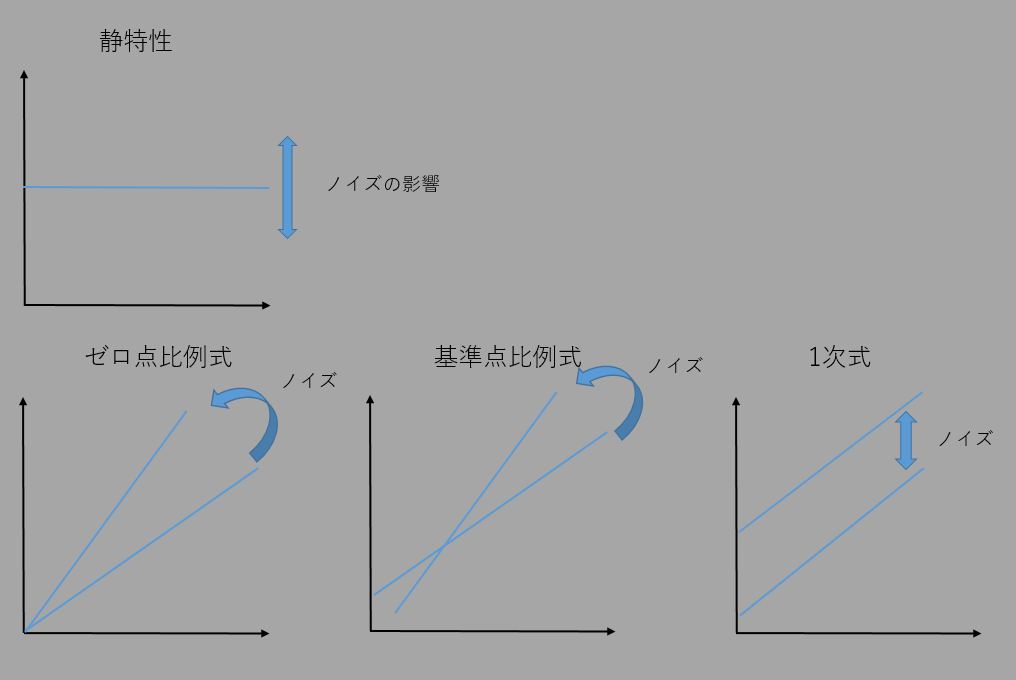
- 静特性(出力が一定)
- 特に正の一定値を望目特性(乾電池とか)
- 動特性(入出力が連続的に関係)
- 入力=0の時、出力も0 ゼロ点比例式
- 入力と出力に初期値があり、交わる点がある 基準点比例式
- 初期値を事前に調節してゼロ点比例式と同じ計算を行う
- 入力・出力が同時に0になることがない 1次式
今回は動特性のゼロ点比例式のL18直交表でのパラメーター設計を例にとって話を進める
ゼロ点比例、1次式で計算が異なり、また、標準SN比などの考え方もあるので自分の目的に適した方法を選択する。
得られた出力のデータを作図してみると思っていた理想関係と違うことがある。
その際は因子の選択を間違えているか、理想関係を見誤っている。
パラメーター設計の流れ
1.出力の評価方法を決める
2.因子洗い出し
3.因子を組み合わせ(直交表に割り付ける)
4.出力を観測
5.観測値の変動や平均・傾きを計算
6.変動・平均・傾きをパラメーターごとに解析(要因効果図)
7.効果のある因子を組み合わせて最適な因子に調整(二段階設計)
具体的な流れ
1.出力の評価方法を決める
2.因子洗い出し
3.因子を組み合わせ(直交表に割り付ける)
1から3までは、そのシステムに詳しい設計者が集まることで問題なく行われると思う。
なるべく抜け漏れなく、影響ある因子を上げることが望ましい。
実験計画法でのわりつけは効果を確認したい因子を何列目に配置するか考慮が必要だが、
知る範囲のパラメーター設計ではここに特に気を付けている例は見当たらなかった。
因子同士に相互作用が考えられる場合は1列目や8列目に因子を割り当てず、ばらつきの計算時のばらつき量から
「因子で説明できなかったばらつき」として確認するしかない。
4.出力を観測
実験を行い、値を得る
5.観測値の変動や平均・傾きを計算
パラメーター設計では変動(ばらつき)として**SN比[単位:デシベル db]が使われる。
また、傾きは感度[単位:デシベル db]**が使われる。
SN比や感度といった指標は解釈が難しく、本当にこの指標で良いのかという議論は未だに解決していない。
しかし数値から結果の評価方法までが簡単なので統計に強い技術者でなくとも理解しやすいという利点がある。
全変動ST
得られた値の二乗和を求める
S_{T} = \sum y^2
N1についてのSN比を計算してみる
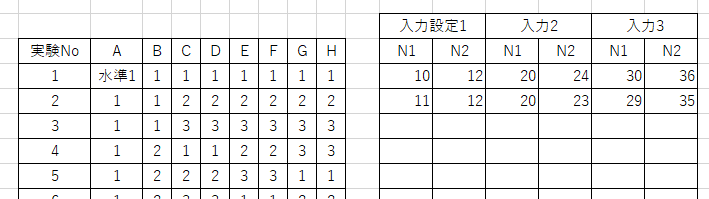
(入力1 × 入力1のN1)+(入力2 × 入力2のN1)+(入力3 × 入力3のN1) = L1 とする
N2についてもL2を計算する
ノイズはN2までの2水準なので、n=2
入力は設定k=3まである。
n(入力1^2 + 入力2^2 + 入力3^2) = r(有効除数) とする
入力の効果Sβ
S_{\beta} = \frac{1}{r}(L_{1}+L_{2})^{2}
誤差変動Se
説明できなかった誤差を計算
S_{e} = S_{T} - S_{\beta}
誤差分散Ve
V_{e} = \frac{S_{e}}{nk-n}
誤差全体の変動
S_{N'} = S_{T} - S_{\beta}
誤差全体の分散
V_{N'} = \frac{S_{N'}}{nk-1}
SN比 SN
10 log_{10} \frac{1}{r} \frac{S_{\beta}-V_{e}}{V_{N'}}
感度 S
10 log_{10} \frac{1}{r} (S_{\beta}-V_{e})
以上のように1実験(1行)に対してSN比と感度を計算する。
SN比の思想は
10 log_{10} (\frac{\beta}{\sigma})^2
感度は
10 log_{10} (\beta)^2
である。
SN比の計算の際には、上記のように複雑な計算をしなくとも、
最小二乗法によって求めた傾きと、
誤差分散Veを使っても設計評価に見逃しが出るほど大きな影響がないことが経験的に知られている。(参考図書参照)
\hat{\beta} = \frac{L1+L2}{r}
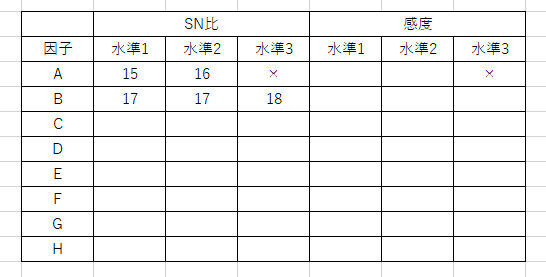
SN比や感度の水準平均として、因子&水準ごとに平均をとる。
例えば因子Bの水準1についてのSN比が知りたければ、実験1,2,3,10,11,12の値を平均化する。
以上から水準平均一覧を求める
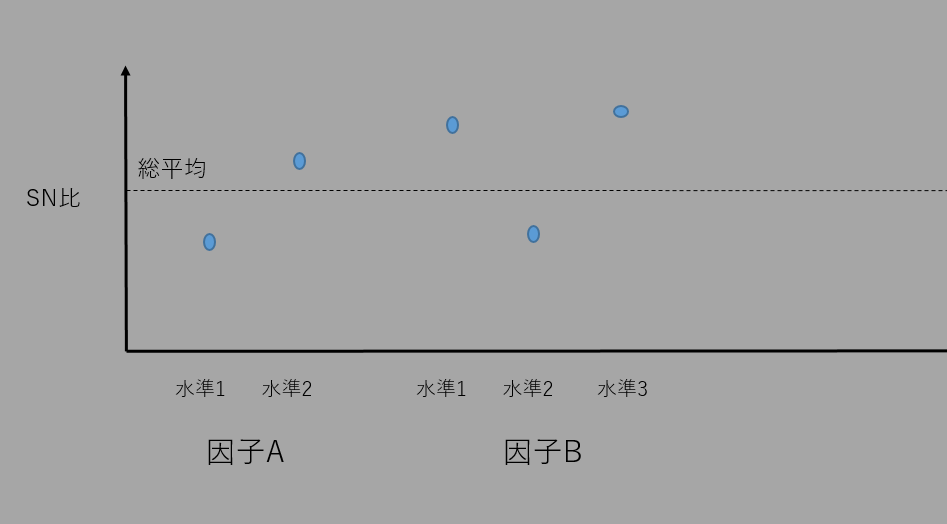
6.変動・平均・傾きをパラメーターごとに解析(要因効果図)
これらの値をもとに以下のような要因効果図を作図する。
感度に関しても要因効果図を作図する
7.効果のある因子を組み合わせて最適な因子に調整(二段階設計)
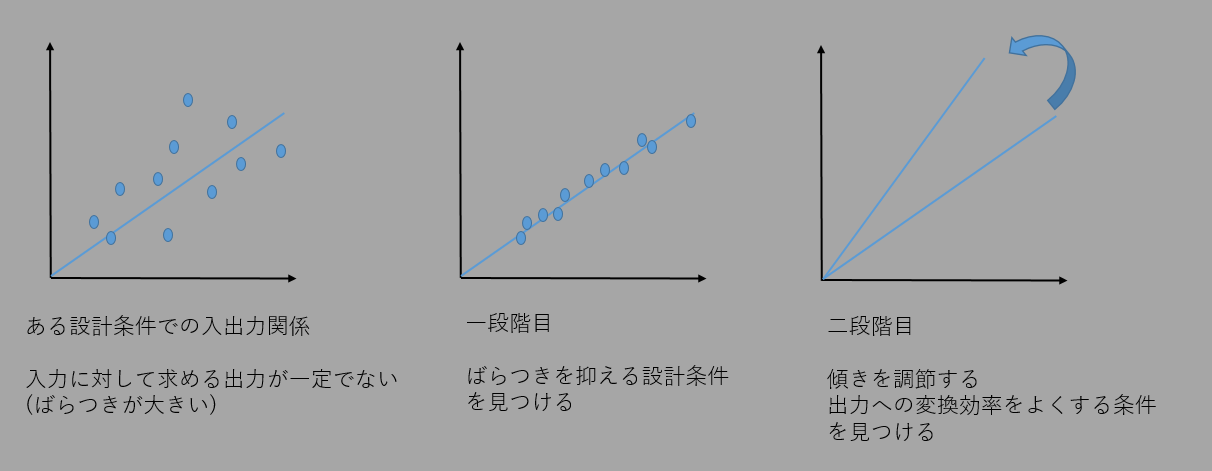
二段階設計とは
従来までの設計条件では入力と出力にばらつきがあるとする
まずばらつきを抑える設計条件を探し、
次に傾きを調節する
という行為を二段階設計と呼ぶ。
まずSN比を見てばらつきが小さくなる水準を選ぶ(SN比が大きいもの)
選ぶ数としては因子数の半分(8因子なので4因子ほど)を選ぶ場合や、譲れない因子がある場合は増やすことも考える。
因子の中でSN比の高いものを決定してから、
残りの因子の中で感度の高い水準を選択する。
感度を調節することは、入力と出力の関係の傾きを大きくすることに相当する。
ゴム動力飛行機の例で言えば
SN比はゴムの巻き数と飛行距離の関係を一定にし、
感度はゴムの巻き数が少なくとも飛行距離が延びるように調節している。
要因効果図の中で、SN比や感度に対して値の変化が大きくない因子は、どの水準を選んでも出力に影響が少ないことがわかる。
設計時には材料や設備コストをもとに選ぶことができる。
最後に、現行条件との比較・評価
実験の中に現行の設計条件がある場合、二段階設計によって最適とした条件と比較する。
(無い場合には実験からわかる最悪の条件を対象にする)
現行条件と最適化した条件とSN比が12.98dbあがったならば
10log_{10} X = 12.98 \\
X=10^{1.298}=19.86 \\
\sqrt{19.86}= 4.45
以上から現行条件よりも4.45倍改善がみられる
もしくは、傾きが同じと考えるなら、ばらつきを4.45分の1に抑えられている
と考える。
感度も同じように評価する。
このようにしてノイズに強い設計を見つけるのがタグチメソッドのパラメーター設計
おまけ:二乗和の分解
厄介な考えが出てくるが簡単に努めるのでついてきていただきたい。
分散分析やタグチメソッドのSN比の考えの元となる二乗和の分解について説明する。
平均μ 分散σ の正規分布からデータが得られた時、i個目の観測データを以下のように表現する
y_{i}=\mu +\epsilon_{i}
ここで誤差εは本当の期待しているμからyiがどれほどずれているか、であるので
y_{i}=\mu + (y_{i}-\mu)
と変形することができる。
n個の標本の平均Tを母平均μとして考えると、
y_{i}=\bar{T} + (y_{i}-\bar{T})
\frac{1}{n}\sum_{k=1}^{n} {y_{i}} = \bar{T} \\
\sum_{k=1}^{n} {y_{i}} = n\bar{T} \\
ここで、後項のyiとTからなる偏差の二乗和について考える
S_{e}=\sum_{k=1}^{n} (y_{i}-\bar{T})^2
これを展開して
S_{e}=\sum_{k=1}^{n} (y_{i})^2 -2\bar{T}\sum_{k=1}^{n} (y_{i}) + \bar{T}^2\sum_{k=1}^{n} 1 \\
=\sum_{k=1}^{n} (y_{i})^2 -2\bar{T}・n\bar{T} + \bar{T}^2・n \\
=\sum_{k=1}^{n} (y_{i})^2 - \sum_{k=1}^{n} (\bar{T})^2
つまり
\sum_{k=1}^{n} (y_{i}-\bar{T})^2=\sum_{k=1}^{n} (y_{i})^2 - \sum_{k=1}^{n} (\bar{T})^2 \\
\sum_{k=1}^{n} (y_{i})^2=\sum_{k=1}^{n} (\bar{T})^2 + \sum_{k=1}^{n} (y_{i}-\bar{T})^2
データyiの二乗和をST
平均の二乗和をSm
偏差の二乗和をSe
とすると
S_{T} = S_{m} + S_{e}
と表すことができる。
以上
参考図書:入門タグチメソッド