【投資・R】統計や機械学習使って"金持ち"になりたい~周期分析~【第3話】

前回までのあらすじ

・株のデータをちょこっとあつめた
・plotした
・前処理した

今回の目的
・周期を知ってパターンを見つける
・パターンから今後上がるのか下がるのかを掴みたい

#周期の分析
データは前回までのスクリプトをそのまま受け継いでいます。

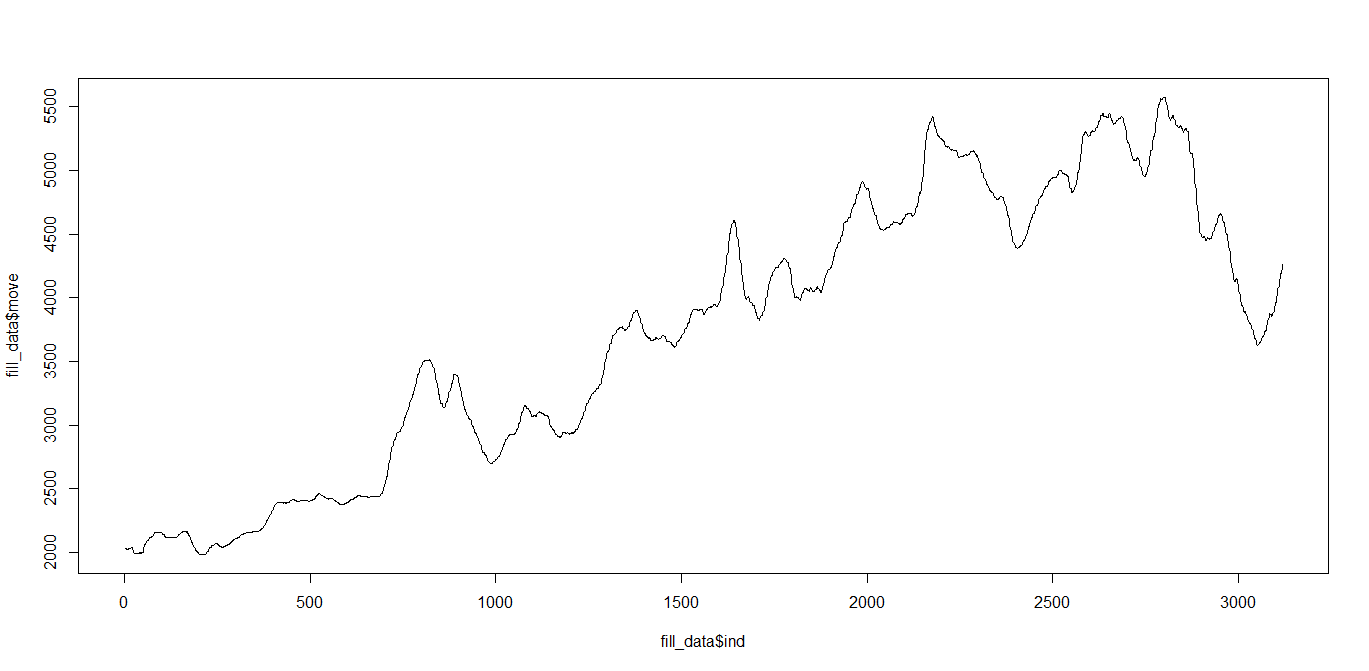
前回の欠損を埋めたデータをもう一度plotしてみます。

plot(fill_data$ind,fill_data$move, type="l")

そもそも周期性があるのかを調べてみます。
周期性はフーリエ変換という便利な数学がありまして、
どの間隔で周期があるのかを見つけてくれる関数があります。

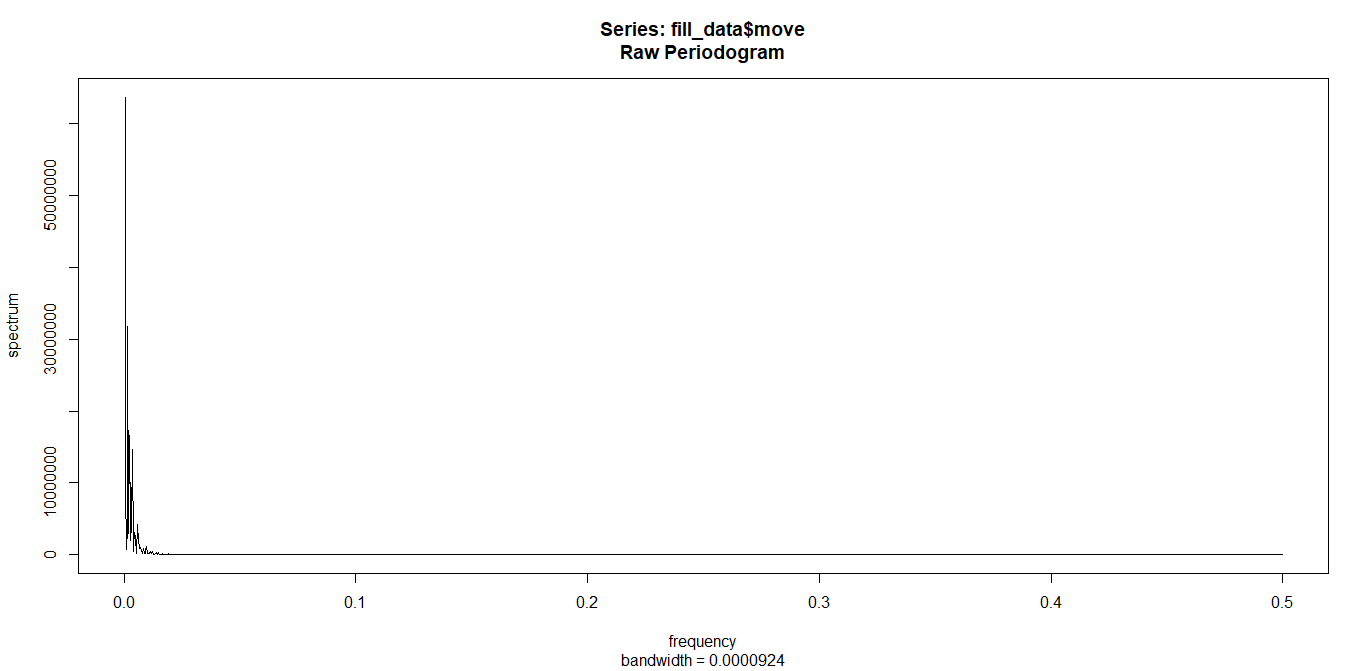
spec.pgram(fill_data$move,log="no")

spec.pgram関数便利。
fftという高速フーリエ変換を行ってくれる関数もありまして、
その関数からデータ数や周波数を使って計算したら同じ図を作図できます。
でもこっちのほうが楽なので。

図の確認方法ですが、データ全体に対して周期性を探したところ、ほとんど0付近に高いピークが現れています。

このピークの出る位置が周期を表してくれるのですが、今回の図からわかるのは周期が無いという事です。
もしもsinカーブのように周期が綺麗にあれば、全体の何割くらいの位置で一周期になっているのか、という事がこの図でわかるようになります。
(相変わらず説明が下手)

#もっと周期成分を深堀

今回はデータに対して直接周期を求めました。
ですが、ファイナンス系のデータは単位根過程という、過去の値±ランダム値から成り立っていることがほとんどのようです。
過去の値というのはつまりオフセットのようなものです。
本来はランダムな値がどんな周期で足しあわされていくのかを知りたいわけです。

もうすこし説明すると、
時系列とはトレンド成分と周期成分から成るものであり、
トレンド成分は過去からの積み上げで、波がどの方向に動くのかを表しています。
データ全体を線形回帰したものと考えると分かりやすいかと。
周期成分は、トレンド成分に足し合わされるパターンを持った波の事。
完全にパターンが無いノイズもある。

トレンドと周期を足したら時系列をモデル化できるので、周期やトレンドが知りたい。

これを知るために階差系列を作ります。

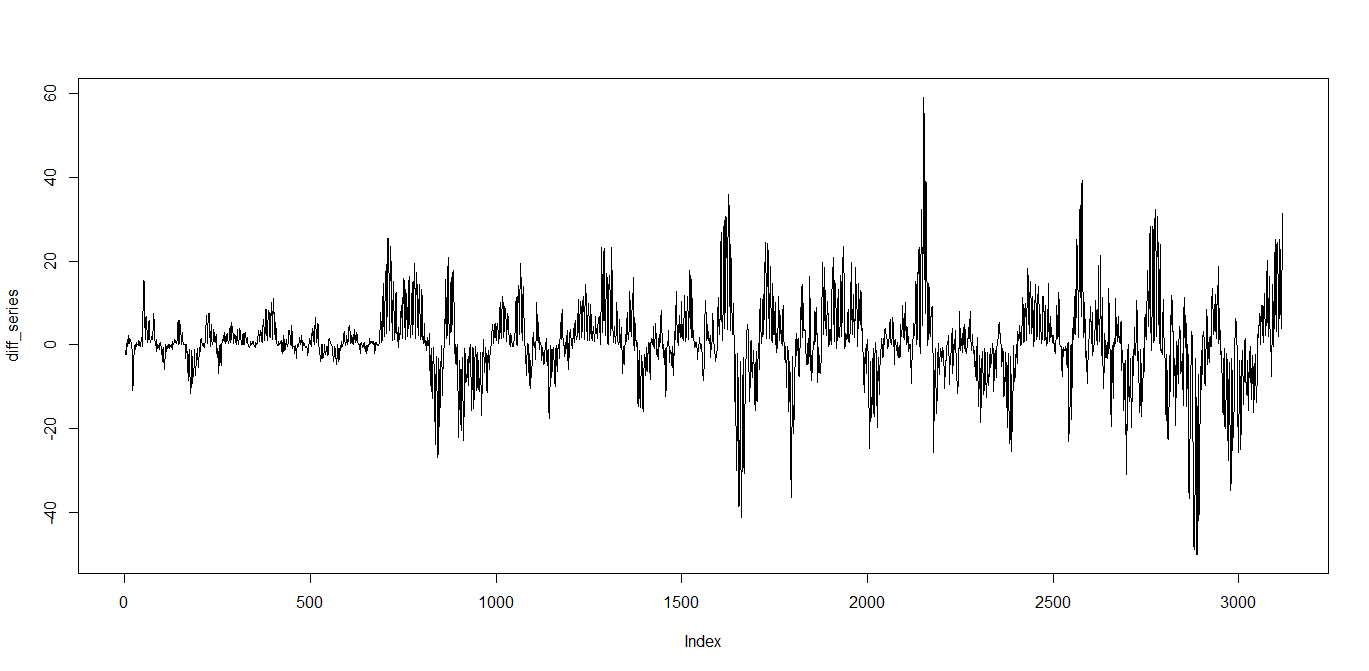
diff_series<-fill_data$move[2:length(fill_data$move)]- fill_data$move[1:length(fill_data$move)-1]
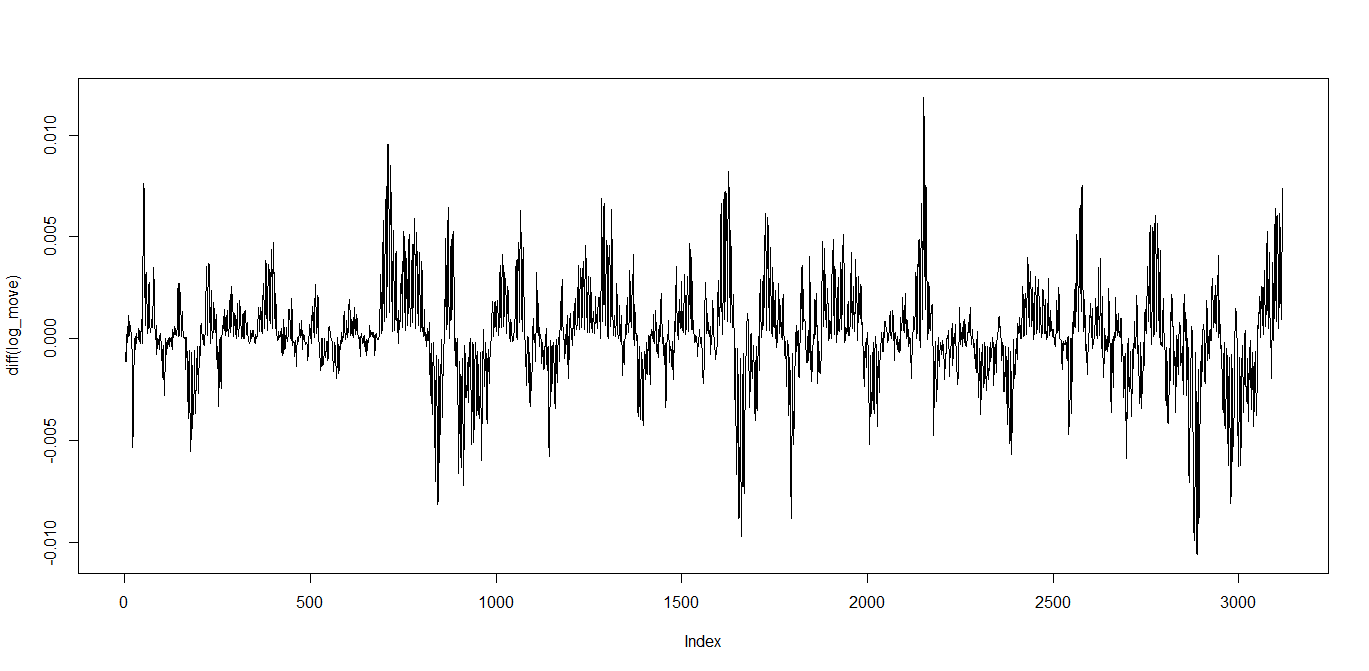
plot(diff_series,type="l")

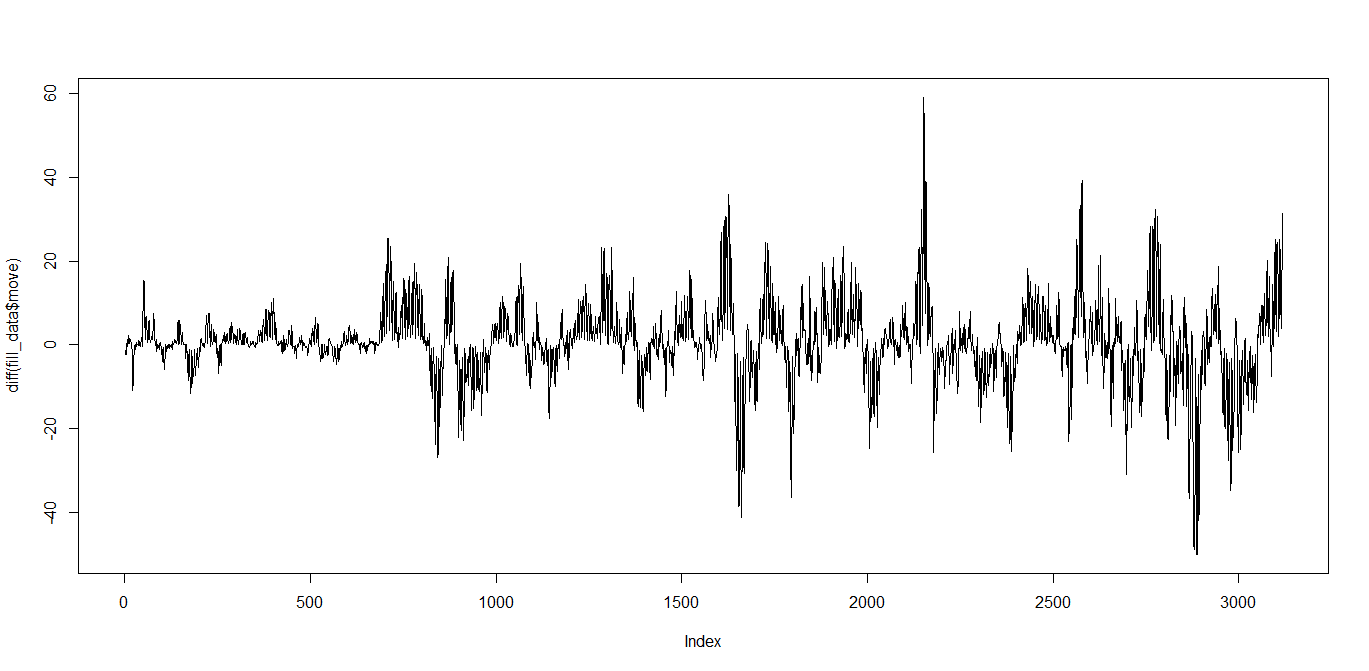
実はもっと簡単に求めるdiff関数も用意されています。

plot(diff(fill_data$move),type="l")

これでトレンド成分がなくなり、周期的に表れる成分だけになりました。
この成分に周期があるのか確認します。

このdiffからも周期成分は見つけられないのでしょうか？

library(animation)
saveGIF(
for(i in seq(2,730,10)){
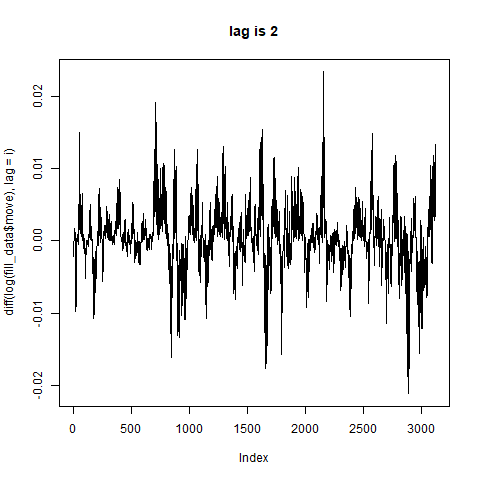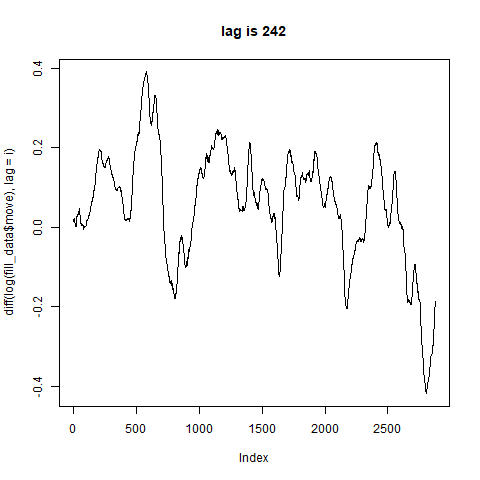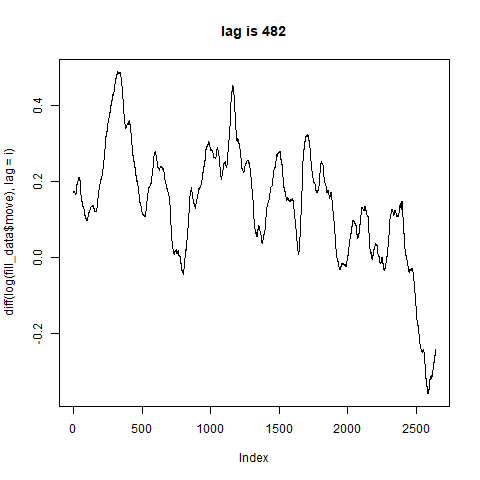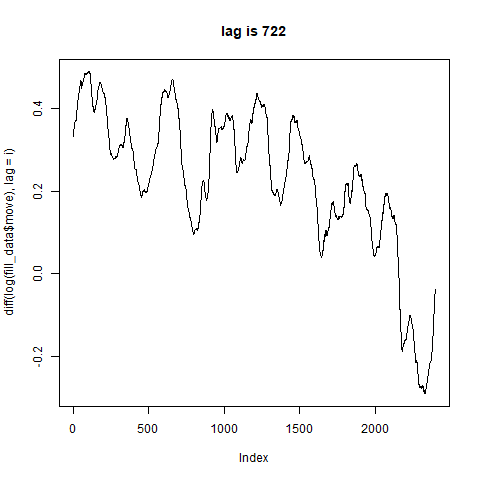
plot(diff(log(fill_data$move),lag=i),main=paste0("lag is ",i),type="l")
}
, movie.name="diff.gif", interval=0.8)

ちょっと分からない。。。

ちなみにsin(x)のようなきれいな周期を持っているデータについて差分を取るとdiffのplotは元のsin(x)とそんなに変わらないまま維持される。
差分を取るとここまでグネグネと形が変化するのであれば綺麗な周期は期待できないかも。

#周期の確認

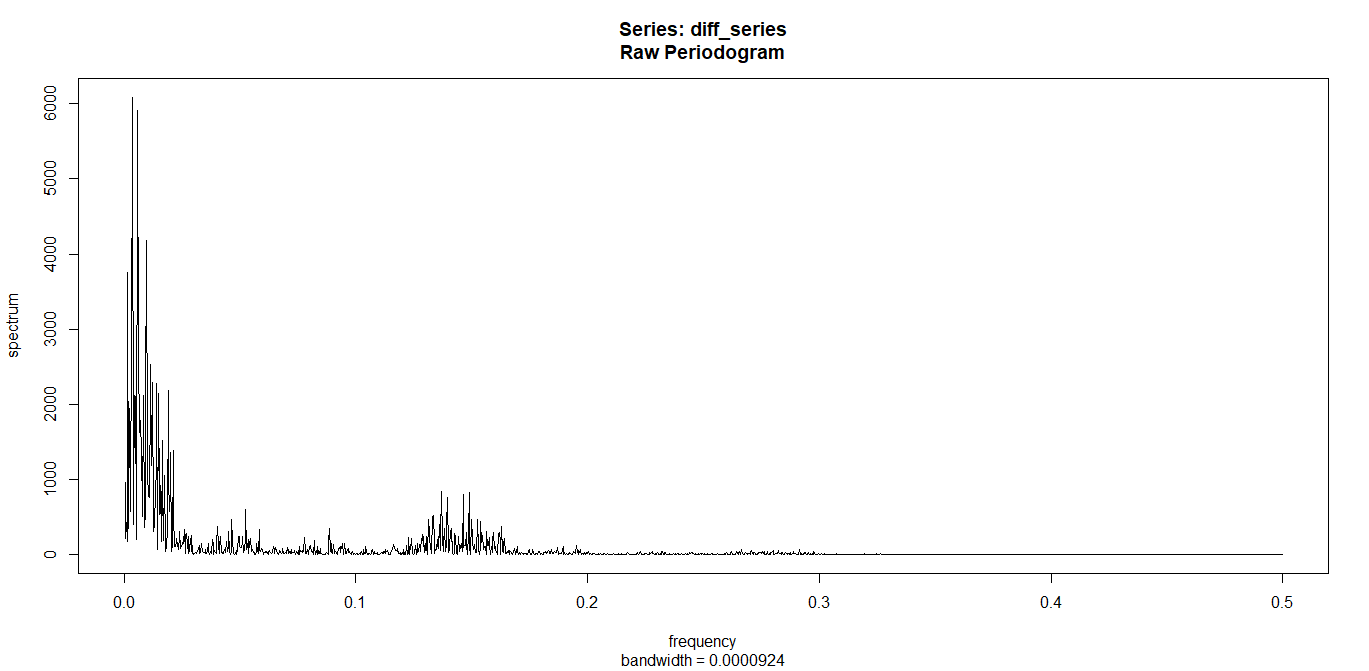
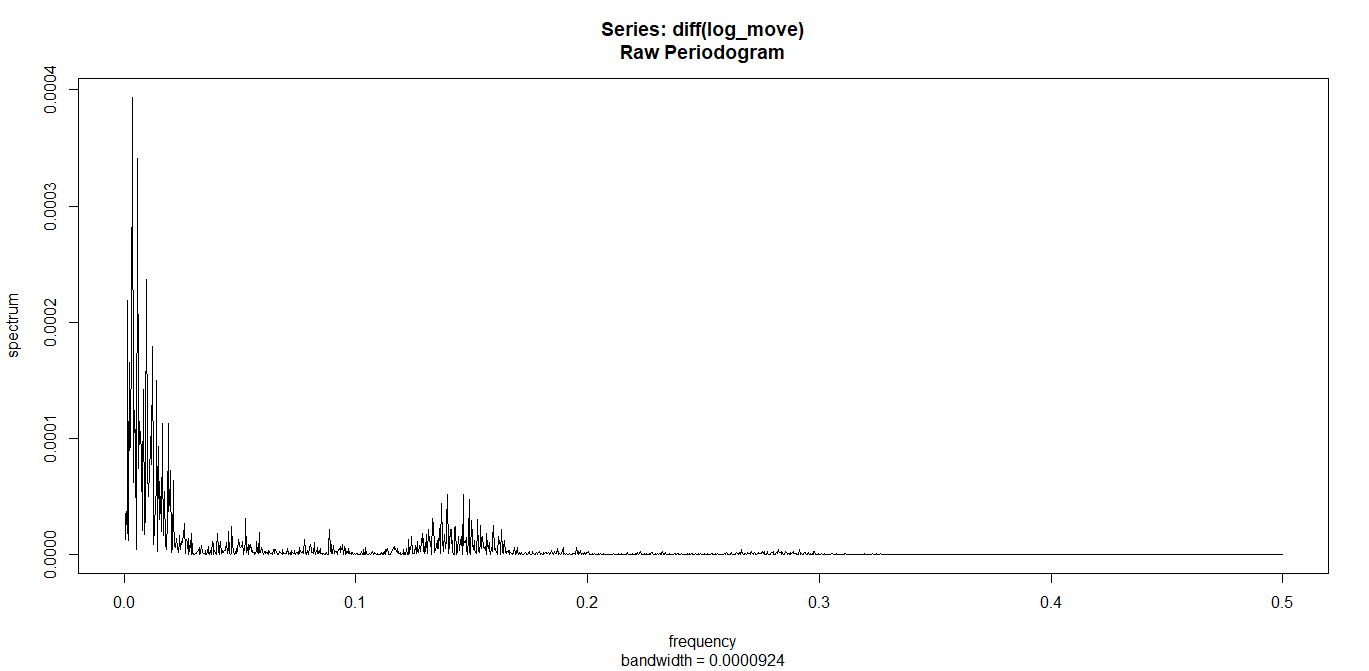
spec.pgram(diff_series,log="no")

周期らしきものが少しだけ見えてきました。
0.15付近に小さい山が見えます。
これはデータ全体(約3000データ)に対して0.15あたりの位置に1周期があるという事です。

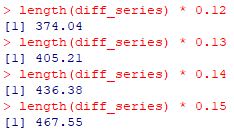
0.15あたりって何データ目かと確認すると、0.12で374という値が出ています。
このデータは株式のデータであり、実はこの企業は一年のうちに上がるタイミングが定期的にありそうだ、という事は事前に考えていました。
なのでこの374はおそらく365日周期を見つけてくれたのではないかと思います。
予想していた仮説を**"それらしい数字"**で確かめることができました。

もちろん、「1年で周期があるだろう」と考えていたために374が365とむすびついてしまった感は否めません。
0.13~0.15までも念のために確認すると467日になっています。
365とは少し離れています。

ここから新しい知見が得られました。
「実は365日周期でなく、400~460日周期なのでは??」
どのくらい役に立つかはわかりませんが、かんがえてもみなかった新しい仮説が得られたというのは大きい収穫です。

#もっともっと深堀

階差系列のplotを見てみると、0~500あたりは値が波が大きくないのに、500~3000までにじわじわと波が大きくなっていっているように感じます。

ファイナンス系の時系列データにはよくある傾向らしいのですが、
高い値をとるようになるとばらつきが大きくなってきて、低い値では安定する。という傾向があるようです。
階差系列のplotの波が大きくなっているのは、トレンド成分が増加しているために、
"よくある傾向"が発生していると考えられます。
ばらつきの大きさの変化による影響から、周期成分がうまく抜き出せなくなります。
ばらつきの大きさを軽減するため、元のデータを対数化してばらつきを小さくします。

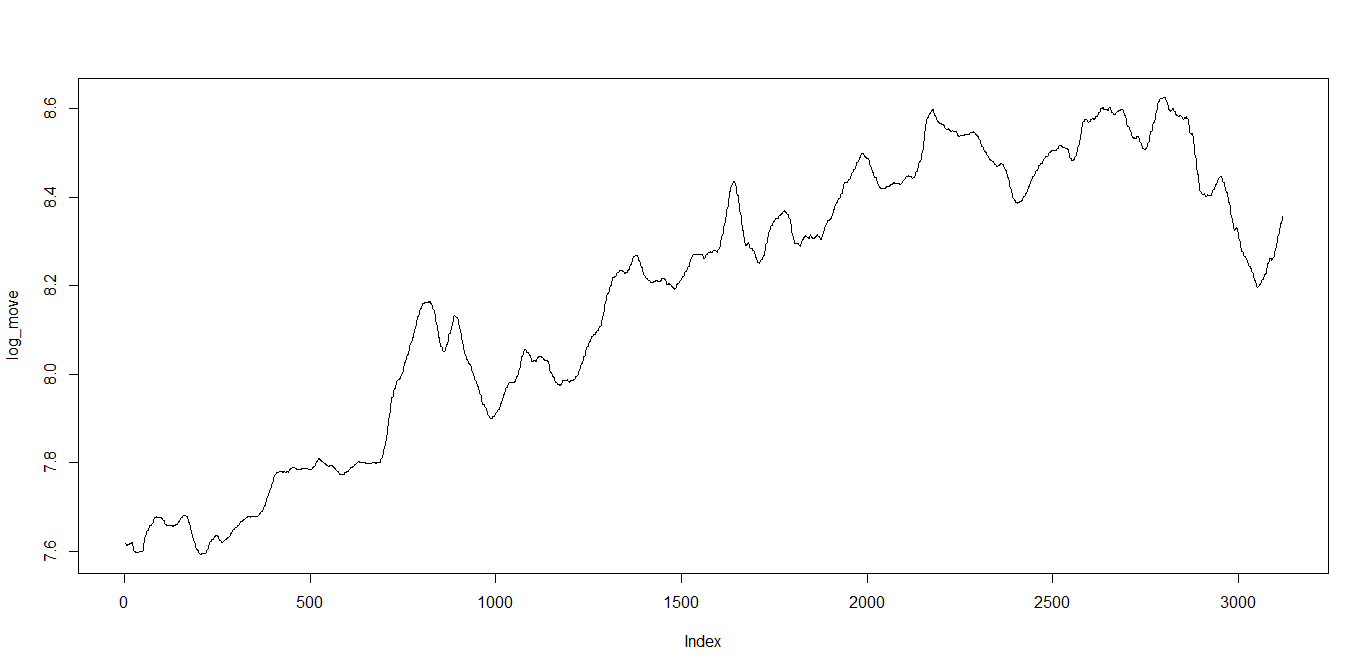
log_move<-log(fill_data$move)
plot(log_move,type="l")
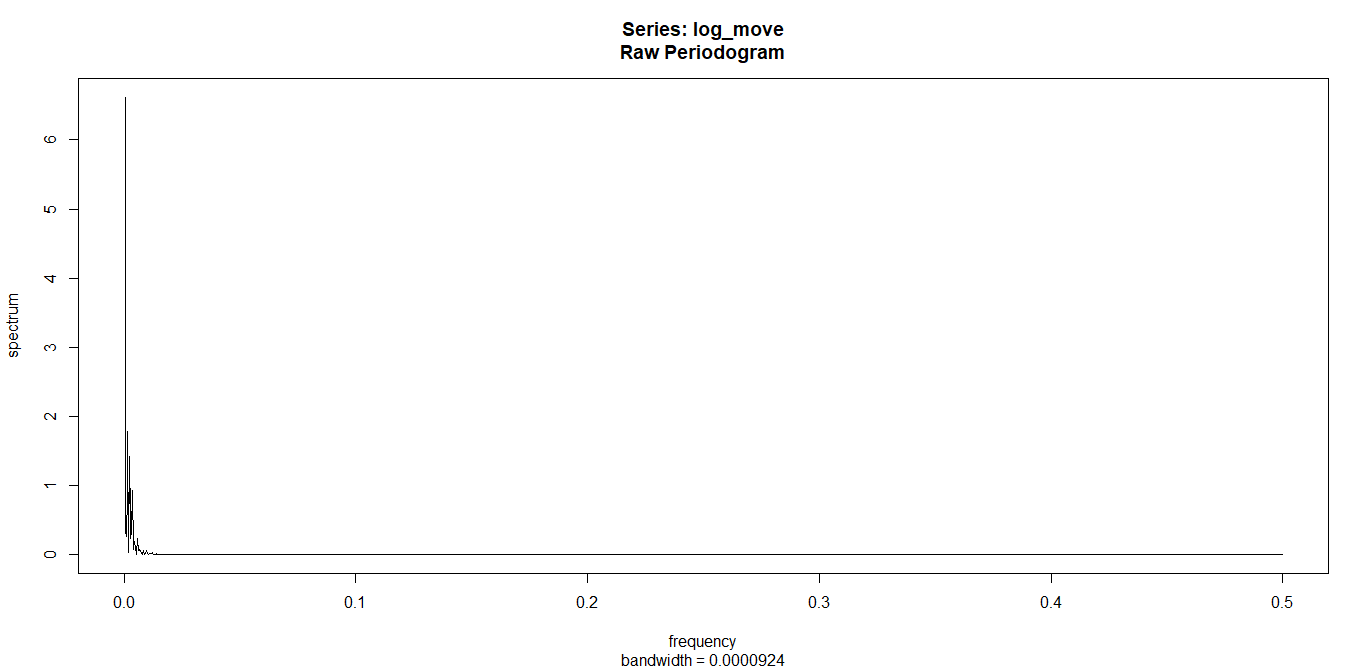
spec.pgram(log_move,log="no")
plot(diff(log_move),type="l")
spec.pgram(diff(log_move),log="no")

対数化しても定常性は見つけられなかったような・・・
なにか間違えているような気もしますが、このまま進めます。

#関数で簡単に分析

今までやってきたことはstl関数で簡単に実行できてしまいます。

move_ts<-ts(as.numeric(fill_data$move),frequency=2)
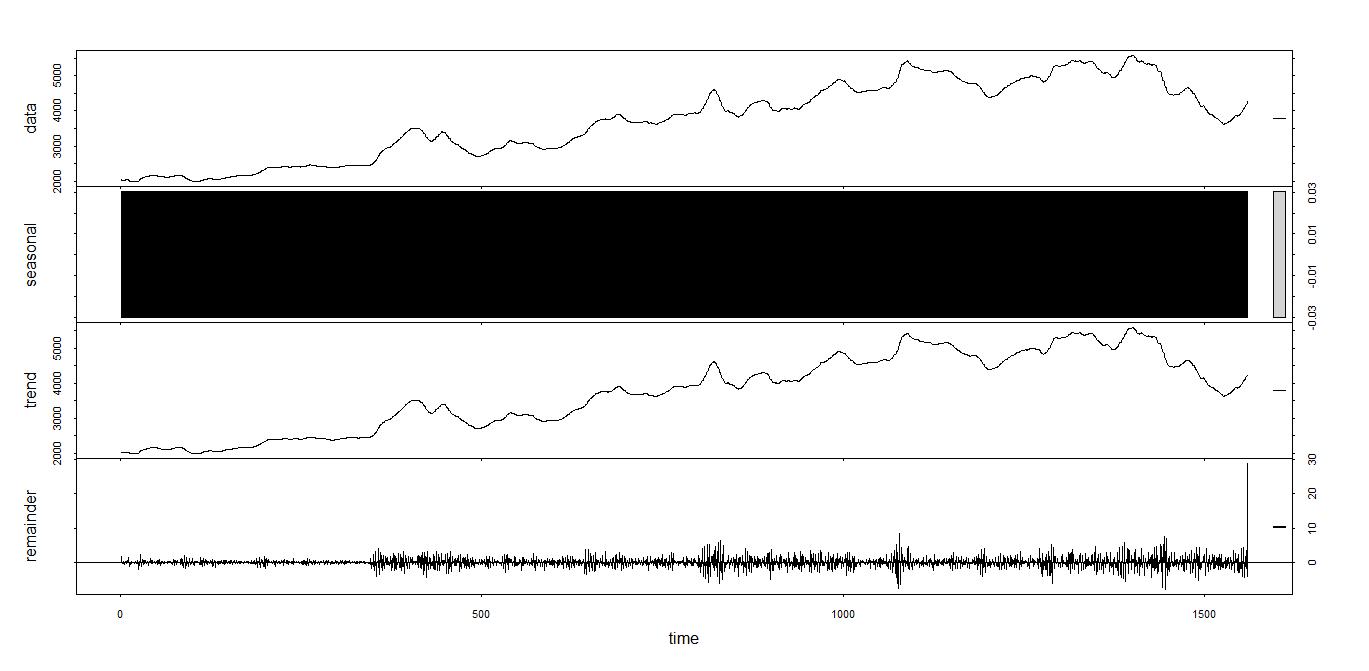
plot(stl(move_ts,s.window="per"))

元データ
季節性：周期的な影響
トレンド：増加、減少の傾向
残差：季節性でもトレンドでも説明できない影響

今回frequencyを2に設定してあるため、2つのデータを一塊にしてデータの傾向を掴んでほしいと指定しています。
2つのデータから季節性を抽出できるはずもないです。
例えば四季のある1年分の気温の時系列から、季節性を抽出したいのであれば、365日を暑いと寒いの2分割に分けるため180に設定するか、
3期や4期に分けるため、120や90に分けるなどです。

2つのデータを一塊にしているため、trendの図でデータのほとんどを説明できてしまい、残差はほとんど無くなっています。
最も適切に周期を掴めた!と言えるのはどんな時かを考えてみると、
・季節性の項目で周期が確認できる
・frequencyが小さすぎない
・トレンドがなめらか
・残差が小さい
を満たしている時だと思います。

まずはfrequencyを変化させることによって、stlがどう動くのか確かめるため、
図をgifにして動かしてみます。

library(animation)

saveGIF(
for(i in seq(2,730,10)){
move_ts<-ts(as.numeric(fill_data$move),frequency=i)
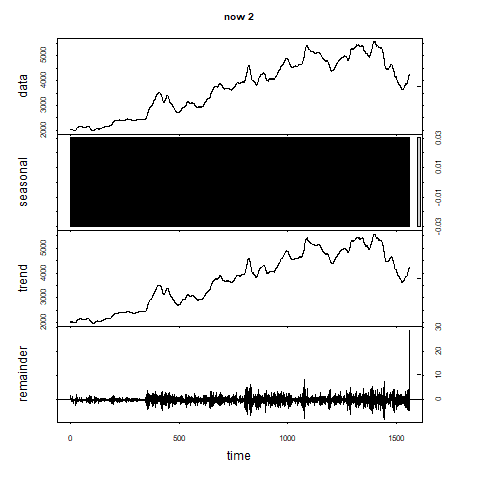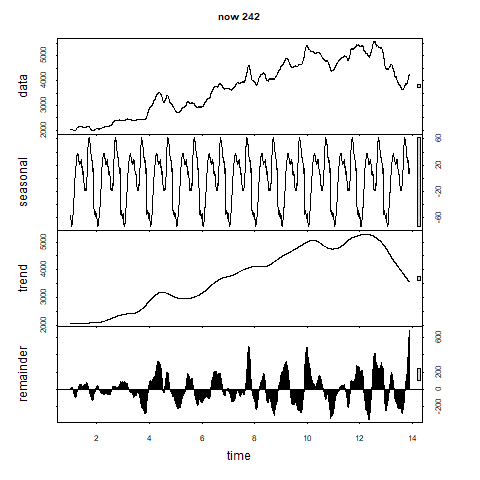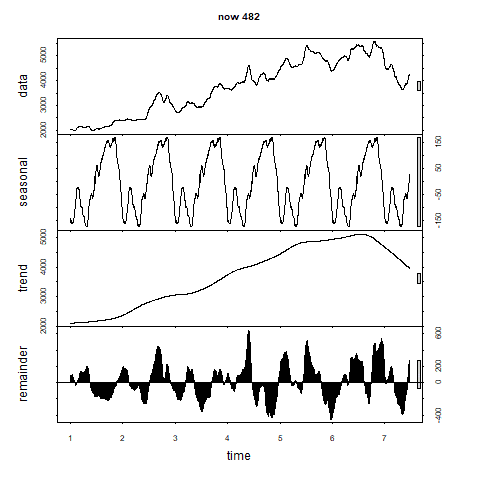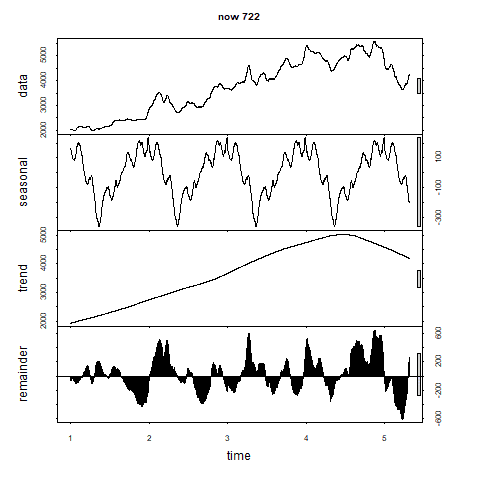
plot(stl(move_ts,s.window="per"),main=paste0("now " ,i))
}
, movie.name="stl.gif", interval=0.8)

こうしてgifで確認してみるとfrequencyが300を超えたあたりからトレンド成分がなだらかになってきます。
500まで行くと直線っぽくなってきます。
行き過ぎでしょうか。
残差の成分はある程度波を打っています。

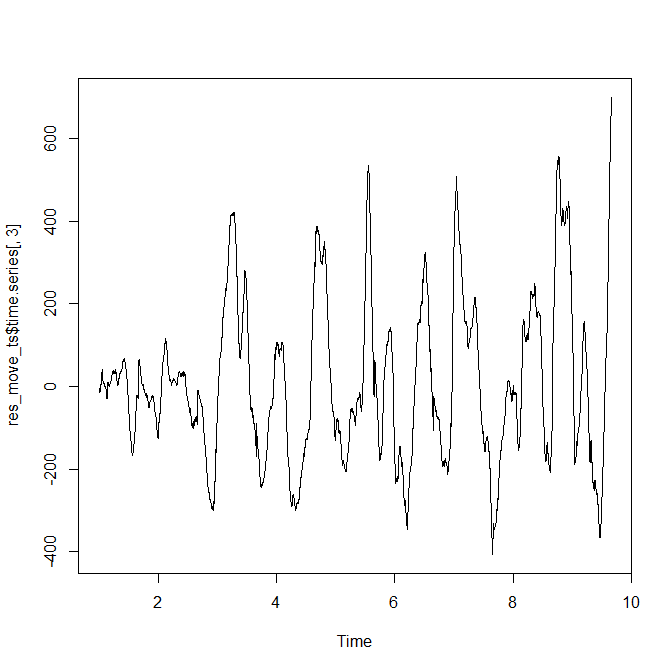
i=360
move_ts<-ts(as.numeric(fill_data$move),frequency=i)
res_move_ts<-stl(move_ts,s.window="per")
plot(res_move_ts$time.series[,3])

この残差に周期を感じてしまいます。
念のため残差成分を取り出して確認してみます。

saveGIF(
for(i in seq(2,730,10)){
move_ts<-ts(as.numeric(fill_data$move),frequency=i)
res_move_ts<-stl(move_ts,s.window="per")
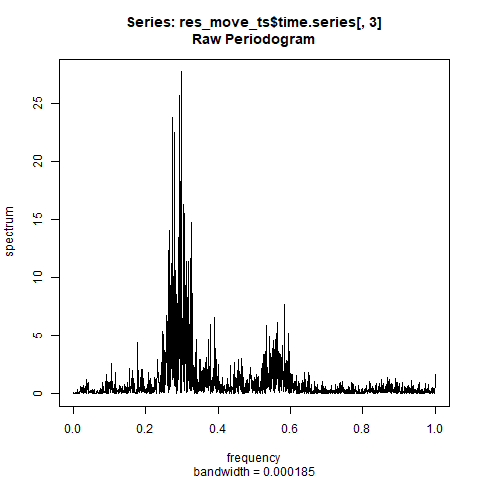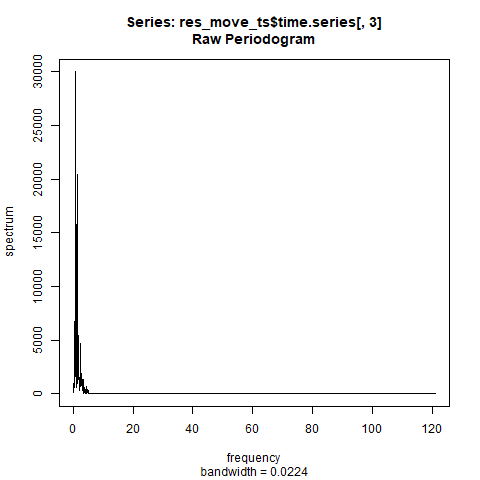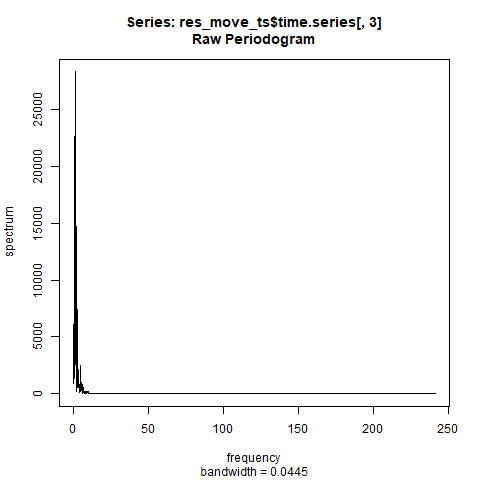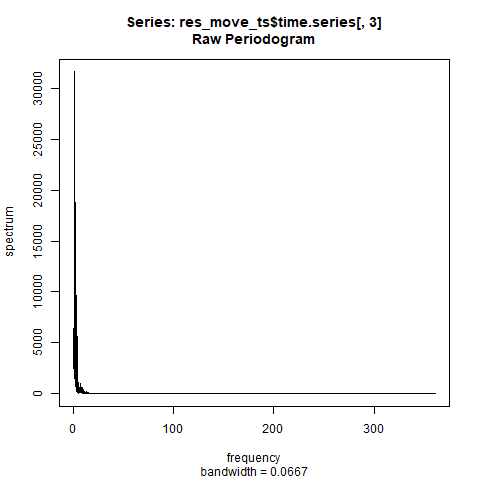
spec.pgram(res_move_ts$time.series[,3],log="no")
}
, movie.name="reminder.gif", interval=0.8)

残差成分はどれだけ動かしても周期はなさそうです。

#差分に定常性などなかった

差分をとって周期をさがしたり、
stlで成分の分解を行いながら周期を見つけようとがんばりましたが、
周期は無さそうな気がしてきました。

単位根過程の検定を行ってみると

library(tseries)
adf.test(fill_data$move)

> adf.test(fill_data$move) 

        Augmented Dickey-Fuller Test

data:  fill_data$move
Dickey-Fuller = -3.1431, Lag order = 14, p-value = 0.0977
alternative hypothesis: stationary

p値がほとんど0です。
差分を見てみます。

adf.test(diff(fill_data$move))

> adf.test(diff(fill_data$move))

        Augmented Dickey-Fuller Test

data:  diff(fill_data$move)
Dickey-Fuller = -7.7499, Lag order = 14, p-value = 0.01
alternative hypothesis: stationary

p値が大変小さくなりました。
つまり、差分系列は「単位根を持つ」という仮説が棄却され、定常である可能性が少しだけ見えてきました。

#周期は・・・見つかりませんでした

気持ちよく周期が見つけられれば、予測モデルを作成する際にありがたいのです。
周期を間違えるとめちゃくちゃな結果になりますので・・・

#次回は予測モデルの作成について