検定してますか?
たとえば、
・アンケート結果
・臨床研究
・生命科学
などなど色々な分野で実験をして、効果検証なり論文化するときには検定をする機会があるかとおもいます。
「教師Aと教師Bから授業を受けた生徒間でテストの点数は異なるのか」
「降血圧薬を飲んだグループと、降血圧薬と聞かされたただの小麦粉の錠剤を飲んだ患者の平均血圧に違いはあるのか」
「ある成分を含んだ食事を与えたマウスと、含んでいない食事のマウスで体脂肪率は変化するか」
などは二群間の平均の差の検定をしたいとなると、t検定をやるのかと思います。
二群ではないとき
もしも検定対象が、
「教師A、教師B、教師C、教師D・・・」と同時並行で実験が行われた時
「通常食,成分1を含む食事,成分2,成分3・・・」などが同時に検証された時
など、教師間、成分間でどのような違いがあったのかを調べることは、一回のt検定ではできません。
また、t検定をA対B、B対C、C対Dと二群ごとに検定してやったらいいのでは?と思うかもしれません。
それ、危険です
正しくは多重比較についての本を読んでいただくとして、
取っ掛かりのためになるべく簡単に危険である理由を説明すると、
二群間の平均値の差の検定は、「比較元集団(コントロール群,対照群)」と、「比較したい集団(何らかの処理した群,投薬群)」の平均値について、「実は比較したい集団の値は一見、大き(小さ)いように見えても、処理の効果に関係なく比較元集団に偶然発生したノイズが加わったものだった」と考える。
しかし、比較したい集団が偶然のばらつきによって発生したと考えても、比較元集団と比べると、ほとんど発生しないような大きな差をとっている時には**「比較元集団にノイズが加わっただけとは言い切れない」**と考えよう。
という概念のもとにあるのが検定である。
そこで出てくるのが信頼区間という概念で、「偶然とは思えない程の大きい(小さい)値の範囲」に比較したい集団の平均値が入った時は「比較元集団と同じ集団から出たデータである」という仮説は棄却してしまおう。となる。
逆に言えば、**"偶然とは思えない程の値も、ほんとに極小さな確率では偶然発生することがある"**のです。
この**"偶然とは思えない"**という言葉について範囲を定めてみる。
比較元集団から100回ランダムでいくつかの値を取り出して平均値を計算した時、大きい・小さい順に並べたとき、大きい側・小さい側の両側から2.5回のデータを"100回中の珍しく離れた値をとったデータと考える"場合、両側の5%を珍しいと定義して、棄却することになる。
これを2群3群だけでなく、7群8群・・・と複数群間で行うと、毎回の検定ごとに稀ではあるが偶然発生しただけの値を**"差が出た"**と言えてしまう確率が群数分だけ蓄積して上昇してしまうのである。
そこで考案されたのが「多重比較の検定」である。
ダネット・チューキー・シェッフェの検定は統計の教科書でもよく見る多重比較の検定である。
多群データを検定する
仮定として、
(サンプルデータ考えるのしんどい)
分散を計算できるようにn=6のサンプルサイズで9種類の比較群を用意した。
生命科学系の論文では一番左のA群がコントロール群であり、それ以外が何かしらの処理が施された群である場合が多い。
今回は薬の強さを確かめる実験と仮定してデータを説明していこうと思う。
value<-c(
1.54,1.47,1.69,1.66,1.56,1.49
2.25,2.31,2.29,2.3,2.33,2.26,
1.58,1.61,1.53,1.59,1.65,1.73,
0.8,0.7,0.7,0.9,0.87,0.79,
2.55,2.74,2.71,2.24,2.13,2.7,
3.25,2.59,3.23,3.1,3.09,3.36,
1.18,0.94,1.02,1.11,0.84,0.99,
4.44,4.59,4.32,4.29,4.51,4.29,
3.99,3.57,3.59,3.42,3.65,3.29)
bind<-NULL
for(i in 1:9){bind<-c(bind,rep(LETTERS[i],6))}
data=data.frame(value=value, name=bind)
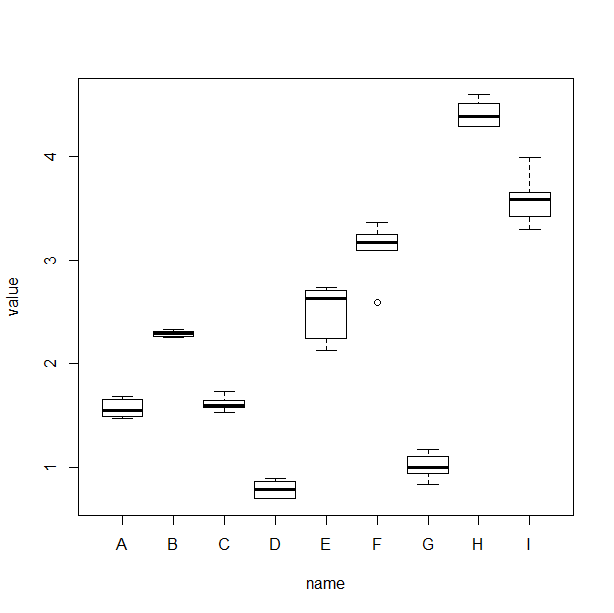
plot(value~name,data=data)
説明変数と被説明変数を指定したplotで箱ひげ図が出力される。
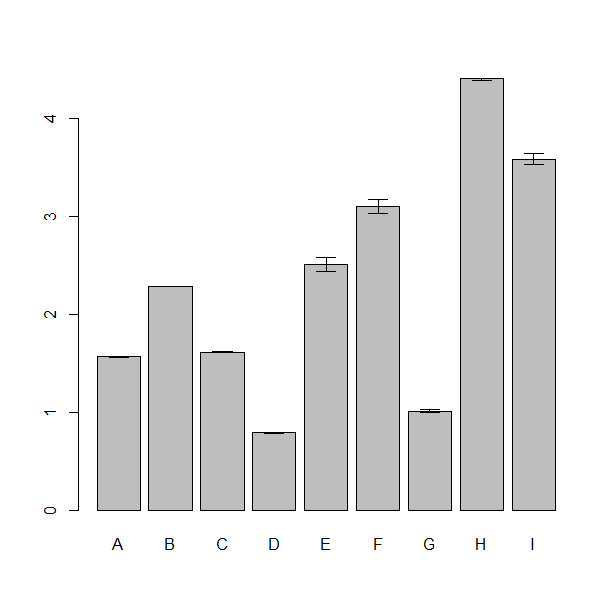
論文でよく見るような棒グラフとエラーバーはこんな感じで書く
mean_cross <- tapply(data$value, data$name, mean)
var_cross <- tapply(data$value, data$name, var)
p<-barplot(mean_cross)
arrows(p, mean_cross - var_cross, p, mean_cross + var_cross, code = 3, lwd = 1, angle = 90, length = 0.1)
クロス集計表をつくってからbarplotに渡す。
このデータに特別な効果を受けたデータがあるのか
データの中に大きな差をもった群があるのか?をまず調べます。
例えばAとB,Cは差を持っていなさそうです。
でもAとDは差を持っていそうです。
さらに後ろのほうのLやOは十分に大きな差を持っていそうです。
この全体に対して、特別な違いを持った群がいるかを求めてみます。
ANOVAで一元配置の分散分析
data_aov <-aov(value~name,data=data)
summary(data_aov)
検定結果にスリースターがつきましたね。
これで何かの群と何かの群で差がありそうだとわかりました。
では、その差のあった群とは何群と何群だったのかをここから比較検定していきます。
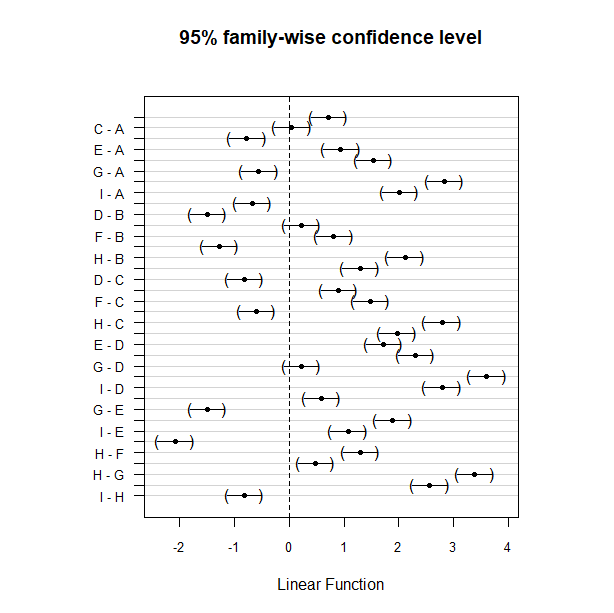
Tukeyで多重比較
library(multcomp)
res <-glht(data_aov, linfct = mcp(name = "Tukey"))
summary(res)
opar <-par(mai=c(1,1.5,1,1),cex.axis=0.8)
plot(res)
んー、この図だけではわかりにくい。
できれば何群と何群が優位だったのかを視覚的にわかるようにしたい。
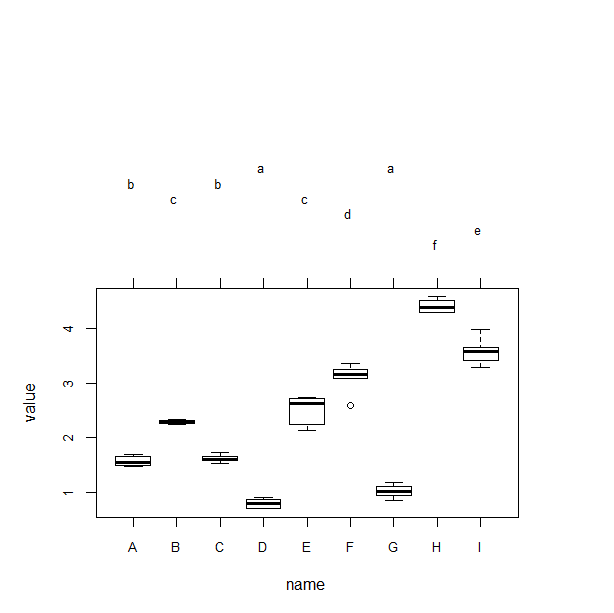
data_aov_cld_res <-cld(res)
opar <-par(mai=c(1,1,3,1))
plot(data_aov_cld_res)
cld(Compact letter display)関数では、何群と何群に差があるかを返してくれる。
plotの図上部に書かれているアルファベットの群とは差が認められなかったということになります。
A群にはbというアルファベットが記入されており、C群にもbが記入されています。A-C群間に差はなかったということです。
分散分析で有意差がでない時
分散分析はデータ中に大きな差を持った群が存在するかを確認してくれます。
分散分析で有意差が確認できなければ、群間の比較検定を行っても有意な差は出ないということではありません。
分散分析と比較検定は違う考え方をしているので分散分析差がないと思い込むと、重要な差を見逃すことになります。
たとえば分散分析に関係なく、一発目から比較検定する検定としてはダネットの比較検定があります。
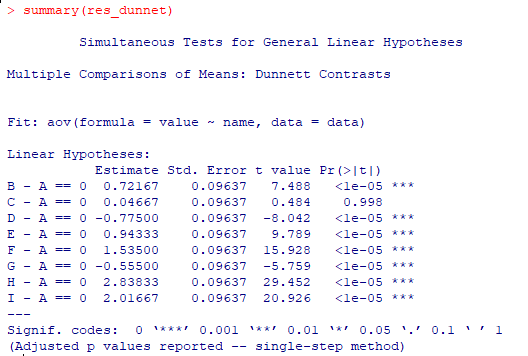
res_dunnet <-glht(data_aov, linfct = mcp(name= "Dunnett"))
summary(res_dunnet)
この結果からA群はC群と差がないことがわかりました。
以上
ということで今回は多重比較検定のお話でした。
詳しい人、間違ってたら教えてください。