Introduction
深層強化学習の分野において,近年ではDeep Q-Network(DQN)などの手法が活用されています.
DQNはAtariのゲームで従来の人工知能による得点を上回り、さらに幾つかのゲームではプロゲーマーと同等またはそれ以上のパフォーマンスを見せたことは記憶に新しいです.
しかし,DQNは行動空間が離散値であり,
ロボットのマニュピレータの操作等,現実では行動空間が連続値として扱われるものが多いです.
行動空間が連続値である強化学習では、Acter Criticのアプローチに基づく手法であるDeep Deter ministic Policy Gradient (DDPG)などがありますが,
Q学習のアプローチに基づく手法であるNormalized Advantage Function (NAF)を実装していきます.
構造的には意外にシンプルであり,DQNを理解しておられる方であれば問題なく理解できると思います.
プログラムの実装は極力kerasを使うことで200行程度でシンプルに記述しました(多少tensorflowを使用しています).
また,私の理解がまだ及んでいない部分がある可能性が非常に高いため「ココが違う!」等のミスがありましたら修正のリクエストをかけていただけるとありがたいです.
※ 今回はDQNを理解されている方を対象としているため,DQNで用いられているExperience ReplayやTarget Network等に関しては省いて説明します.
Normalized Advantage Function (NAF)とは
NAFは深層強化学習のなかでも連続値の行動空間に対応したQ学習です.
また,DQNをベースとした手法であり、Double DQNを拡張したのがNAFとなります.
DQNからNAFまでの軌跡はこのようになっているようです.
図はQiita - 強化学習の系図から引用させていただきました.大変参考になります.
NAFのメリットとしては,同じ行動空間が連続値の深層強化学習であるDDPGと比べ,収束にかかるエピソード数が少ないと言われています.
NAFの特徴
DQNをベースとしているため,Experience ReplayやTarget Network等が同様に用いられます.
大枠としては,状態と実際にとった行動を入力とし、ネットワーク内で予測された行動のQ値を出力する多入力・単出力型のネットワークとなっています.
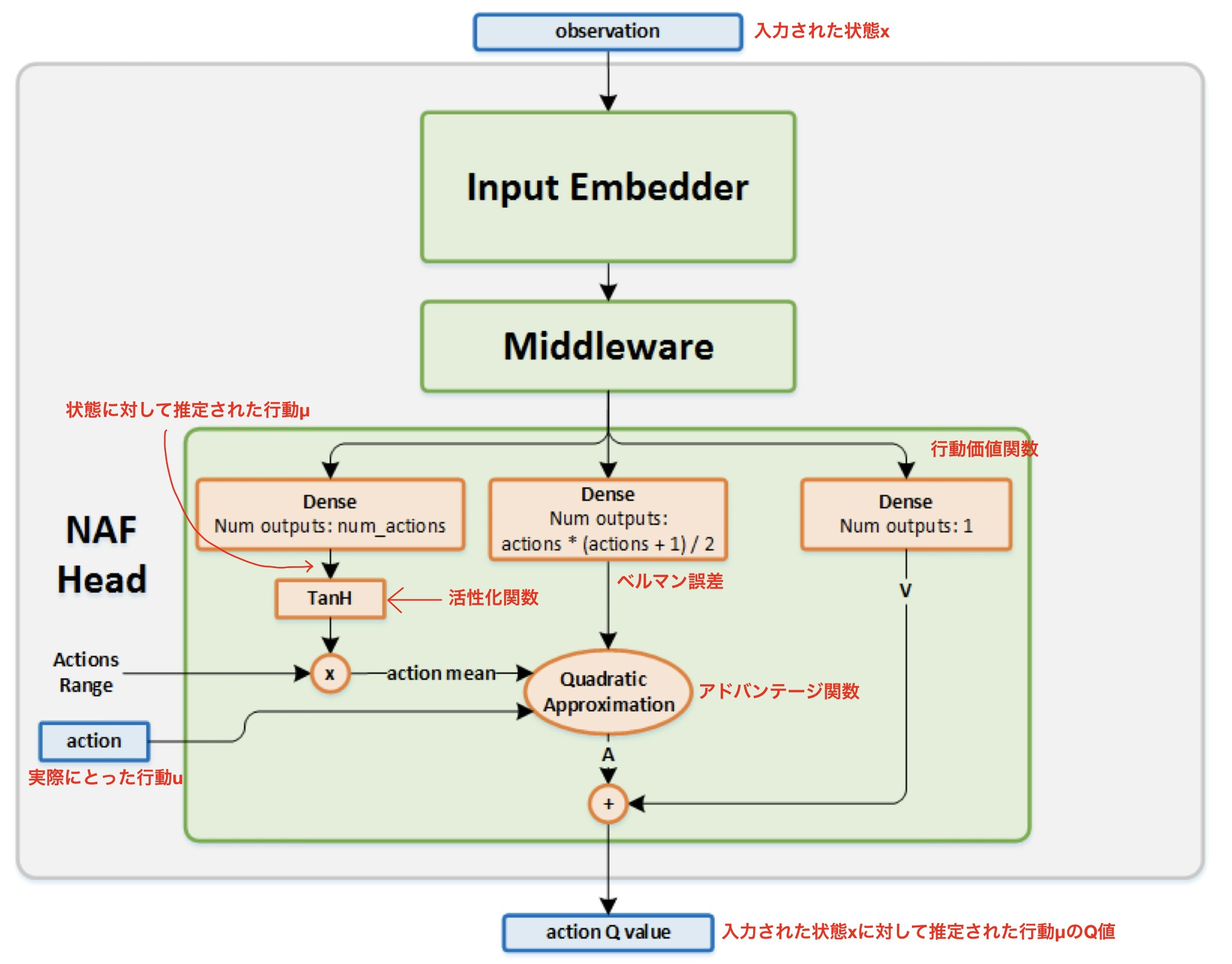
図はIntel AI Lab, Reinforcement Learning Coachから引用
また,NAFはMiddlewareの後に3つに分岐し,これらの出力を用いて予測された行動のQ値を求めるNAF Headが存在しています.
この3つは
1つ目は入力した状態に対して最適な行動を出力する層(活性化関数はTanH)
2つ目はベルマン誤差を出力する層(活性化関数はlinear)
3つ目は行動価値を出力する層(活性化関数は指定無し,とりあえずlinear)
となっています.
ちなみに,このネットワークを見ると「入力した状態に対して予測された行動が出力されてないんじゃ?」と思うかもしれませんが,
”入力した状態に対して最適な行動を出力(予測)する層”
から出力を抜き出してしまえば良いわけですね(実装の仕方はプログラム参照).
それでは,このネットワークの出力からQ値を求めてみましょう. そのために,以下の式を使っていきます.
まず,ネットワークにより出力されたベルマン誤差 $L$を用いて状態依存値(state-dependent)$P$を求めます.
P(\textbf{x}|\theta^{P}) = L(\textbf{x}|\theta^{P})L(\textbf{x}|\theta^{P})^T
↓
次に,ネットワークにより出力された予測された最適な行動を $\mu$,
状態$\textbf{x}$で実際にとった行動$\textbf{u}$,
さきほど求めた状態依存値$P$,
を用いてアドバンテージ関数(advantage function)$A$によりアドバンテージを求めます.
A(\textbf{x}, \textbf{u} | \theta^A ) = -\frac{1}{2}(\textbf{u}-\mu(\textbf{x} | \theta^{\mu})) \cdot P(\textbf{x} | \theta^{P})\cdot (\textbf{u}-\mu(\textbf{x} | \theta^{\mu}))
↓
最後に,ネットワークにより出力された行動価値$V$とアドバンテージ$A$を合わせてQ値を求めます.
Q(\textbf{x}, \textbf{u} | \theta^{Q}) = A(\textbf{x}, \textbf{u} | \theta^A ) + V(\textbf{x} | \theta^V)
これでQ値が求まります.
実装
では実際に実装をしていきましょう.
今回環境に用いるのはOpenAI GymのPendulum-v0です.
https://github.com/openai/gym/wiki/Pendulum-v0
元論文より、大まかなアルゴリズムはこのようになっています。

実装した学習用プログラム
# -*- coding: utf-8 -*-
import numpy as np
import gym
import random
import keras
from keras import backend as K
from keras.layers.convolutional import Conv2D
from keras.models import Model
from keras.layers import Input, Dense, Lambda
import tensorflow as tf
from keras.optimizers import Adam
from collections import deque
import sys
sys.path.remove('/opt/ros/kinetic/lib/python2.7/dist-packages')
import cv2
from skimage.color import rgb2gray
from skimage.transform import resize
gamma = 0.99
np.set_printoptions(suppress=True)
resize_x = 84
resize_y = 84
file_history = open("history.txt", "w")
file_history.close()
class Agent:
def __init__(self, env):
self.env = env
self.input_dim = env.observation_space.shape
self.state_dim = 3
self.actions_dim = 1
self.q_net_q, self.q_net_a, self.q_net_v = self.createModel()
self.t_net_q, self.t_net_action, self.t_net_v = self.createModel()
# 損失関数
adam = Adam(lr=0.001, clipnorm=1.)
# モデル生成
self.q_net_q.compile(optimizer=adam, loss='mae')
self.t_net_q.compile(optimizer=adam, loss='mae')
def createModel(self):
x = Input(shape=(self.state_dim,), name='observation_input')
u = Input(shape=(self.actions_dim,), name='action_input')
# Middleware
h = Dense(32, activation="relu")(x)
h = Dense(32, activation="relu")(h)
h = Dense(32, activation="relu")(h)
# NAF Head
# < Value function >
V = Dense(1, activation="linear", name='value_function')(h)
# < Action Mean >
mu = Dense(self.actions_dim, activation="tanh", name='action_mean')(h)
# < L function -> P function >
l0 = Dense(int(self.actions_dim * (self.actions_dim + 1) / 2), activation="linear", name='l0')(h)
l1 = Lambda(lambda x: tf.contrib.distributions.fill_triangular(x))(l0)
L = Lambda(lambda x: tf.matrix_set_diag(x, tf.exp(tf.matrix_diag_part(x))))(l1)
P = Lambda(lambda x: tf.matmul(x, tf.matrix_transpose(x)))(L)
# < Action function >
u_mu = keras.layers.Subtract()([u, mu])
u_mu_P = keras.layers.Dot(axes=1)([u_mu, P]) # transpose 自動でされてた
u_mu_P_u_mu = keras.layers.Dot(axes=1)([u_mu_P, u_mu])
A = Lambda(lambda x: -1.0/2.0 * x)(u_mu_P_u_mu)
# < Q function >
Q = keras.layers.Add()([A, V])
# Input and Output
model_q = Model(input=[x, u], output=[Q])
model_mu = Model(input=[x], output=[mu])
model_v = Model(input=[x], output=[V])
model_q.summary()
model_mu.summary()
model_v.summary()
return model_q, model_mu, model_v
def getAction(self, state):
action = self.q_net_a.predict_on_batch(state[np.newaxis,:])
return action
def Train(self, x_batch, y_batch):
return self.q_net_q.train_on_batch(x_batch, y_batch)
def PredictT(self, x_batch):
return self.t_net_q.predict_on_batch(x_batch)
def WeightCopy(self):
self.t_net_q.set_weights(self.q_net_q.get_weights())
def CreateBatch(agent, replay_memory, batch_size):
minibatch = random.sample(replay_memory, batch_size)
state, action, reward, state2, end_flag = map(np.array, zip(*minibatch))
x_batch = state
next_v_values = agent.t_net_v.predict_on_batch(state2)
y_batch = np.zeros(batch_size)
for i in range(batch_size):
y_batch[i] = reward[i] + gamma * next_v_values[i]
return [x_batch, action], y_batch
def main():
n_episode = 150 # 繰り返すエピソード回数
max_memory = 20000 # リプレイメモリの容量
batch_size = 256 # いい感じに収束しないときはバッチサイズいろいろ変えてみて
max_sigma = 0.99 # 付与するノイズの最大分散値
sigma = max_sigma
reduce_sigma = max_sigma / n_episode # 1エピソードで下げる分散値
env = gym.make("Pendulum-v0") # 環境
agent = Agent(env)
# リプレイメモリ
replay_memory = deque()
# ゲーム再スタート
for episode in range(n_episode):
print("episode " + str(episode))
end_flag = False
state = env.reset()
sigma -= reduce_sigma
if sigma < 0:
sigma = 0
while not end_flag:
# 行動にノイズを付与
action = agent.getAction(state) + np.random.normal(0, sigma, size=1)
action = action[:,0]
# Pendulumの行動が-2~2の範囲なので変換
action = np.clip(action, -1.0, 1.0) * 2
state2, reward, end_flag, info = env.step(action)
# 前処理
# リプレイメモリに保存
replay_memory.append([state, action, reward, state2, end_flag])
# リプレイメモリが溢れたら前から削除
if len(replay_memory) > max_memory:
replay_memory.popleft()
# リプレイメモリが溜まったら学習
if len(replay_memory) > batch_size*4:
x_batch, y_batch = CreateBatch(agent, replay_memory, batch_size)
agent.Train(x_batch, y_batch)
state = state2
# 可視化をする場合はこのコメントアウトを解除
env.render()
# 4episodeに1回ターゲットネットワークに重みをコピー
if episode != 0 and episode % 4 == 0:
agent.WeightCopy()
# Q-networkの重みをTarget-networkにコピー
agent.t_net_q.save_weights("weight.h5")
env.close()
agent.WeightCopy()
# Q-networkの重みをTarget-networkにコピー
agent.t_net_q.save_weights("weight.h5")
if __name__ == '__main__':
main()
学習結果
こちらのテスト用プログラムを動かせば学習時に含ませたノイズがない状態で結果が見れます.
# -*- coding: utf-8 -*-
import numpy as np
import gym
import keras
import tensorflow as tf
from keras.models import Model
from keras.layers import Input, Dense, Lambda
from keras.optimizers import Adam
from collections import deque
class Agent:
def __init__(self, env):
self.env = env
self.input_dim = env.observation_space.shape
self.state_dim = 3
self.actions_dim = 1
self.t_net_q, self.t_net_a, self.t_net_v = self.createModel()
self.t_net_q.load_weights("weight.h5") # 学習した重みのロード
def createModel(self):
x = Input(shape=(self.state_dim,), name='observation_input')
u = Input(shape=(self.actions_dim,), name='action_input')
# Middleware
h = Dense(32, activation="relu")(x)
h = Dense(32, activation="relu")(h)
h = Dense(32, activation="relu")(h)
# NAF Head
# < Value function >
V = Dense(1, activation="linear", name='value_function')(h)
# < Action Mean >
mu = Dense(self.actions_dim, activation="tanh", name='action_mean')(h)
# < L function -> P function >
l0 = Dense(int(self.actions_dim * (self.actions_dim + 1) / 2), activation="linear", name='l0')(h)
l1 = Lambda(lambda x: tf.contrib.distributions.fill_triangular(x))(l0)
L = Lambda(lambda x: tf.matrix_set_diag(x, tf.exp(tf.matrix_diag_part(x))))(l1)
P = Lambda(lambda x: tf.matmul(x, tf.matrix_transpose(x)))(L)
# < Action function >
u_mu = keras.layers.Subtract()([u, mu])
u_mu_P = keras.layers.Dot(axes=1)([u_mu, P]) # transpose 自動でされてた
u_mu_P_u_mu = keras.layers.Dot(axes=1)([u_mu_P, u_mu])
A = Lambda(lambda x: -1.0/2.0 * x)(u_mu_P_u_mu)
# < Q function >
Q = keras.layers.Add()([A, V])
# Input and Output
model_q = Model(input=[x, u], output=[Q])
model_mu = Model(input=[x], output=[mu])
model_v = Model(input=[x], output=[V])
model_q.summary()
model_mu.summary()
model_v.summary()
return model_q, model_mu, model_v
def getAction(self, state):
action = self.t_net_a.predict_on_batch(state[np.newaxis,:])
return action
def main():
env = gym.make("Pendulum-v0") # 環境
agent = Agent(env)
# ゲーム再スタート
while 1:
end_flag = False
state = env.reset()
while not end_flag:
action = agent.getAction(state)
action = action[:,0]
# Pendulumの行動が-2~2の範囲なので変換
action = np.clip(action, -1.0, 1.0) * 2
state2, reward, end_flag, info = env.step(action)
state = state2
env.render()
env.close()
if __name__ == '__main__':
main()
学習結果としてはこのようになっています(学習されないことがあるので,その場合は何度か学習し直してみてください).
参考文献
元論文
https://arxiv.org/abs/1603.00748
NAFを用いた日本語論文
https://www.ai-gakkai.or.jp/jsai2017/webprogram/2017/pdf/642.pdf
NAFの図
https://nervanasystems.github.io/coach/components/agents/value_optimization/naf.html#choosing-an-action
実装で参考にしたもの
https://gym.openai.com/evaluations/eval_CzoNQdPSAm0J3ikTBSTCg/
https://github.com/NervanaSystems/coach/blob/master/rl_coach/agents/naf_agent.py
https://github.com/carpedm20/NAF-tensorflow/blob/master/src/network.py
活性化関数での参考
https://pdfs.semanticscholar.org/e1af/36deaf167b4a671d25cb98f392d4a3ffac4a.pdf
中間レイヤーを出力する方法
https://keras.io/ja/getting-started/faq/#_7

