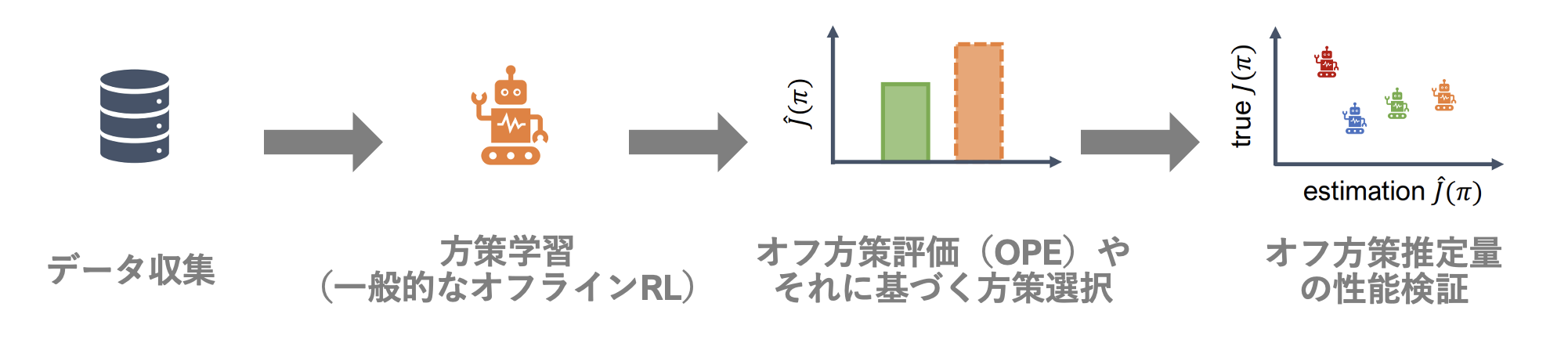
先日 SCOPE-RL というオフライン強化学習とオフ方策評価に関するライブラリを博報堂テクノロジーズ,半熟仮想,東工大中田研との共同研究として公開しました[プレスリリース].
上記ライブラリで扱うオフ方策評価(OPE) は過去に集めたデータのみから新しい意思決定方策を評価する手法として幅広い場面での応用が期待されている技術です.そこで本記事では,主にSCOPE-RLで実装されているOPE推定量を中心に,強化学習のオフ方策評価について基礎から発展的な内容まで解説したいと思います.最後の章の関連研究と今後の展望 ではオフ方策評価の今後について自身の注目するトピックをまとめており,開発者ならではの視点として読んでいただけたら嬉しいです.
強化学習・オフ方策評価ともに初めての方にも,大まかな内容を理解していただける構成になっています.概要を掴みたい方は適宜証明を飛ばしつつ,最後まで読んでいただけたら幸いです.
目次
- オフ方策評価(Off Policy Evaluation)
- 問題設定
- オフ方策評価の推定量
- まとめ
- 関連研究と今後の展望
- appendix : SCOPE-RLの紹介
オフ方策評価(Off Policy Evaluation)
まずはオフ方策評価についてオンラインで方策を評価するオンライン実験と比較する形で紹介します.
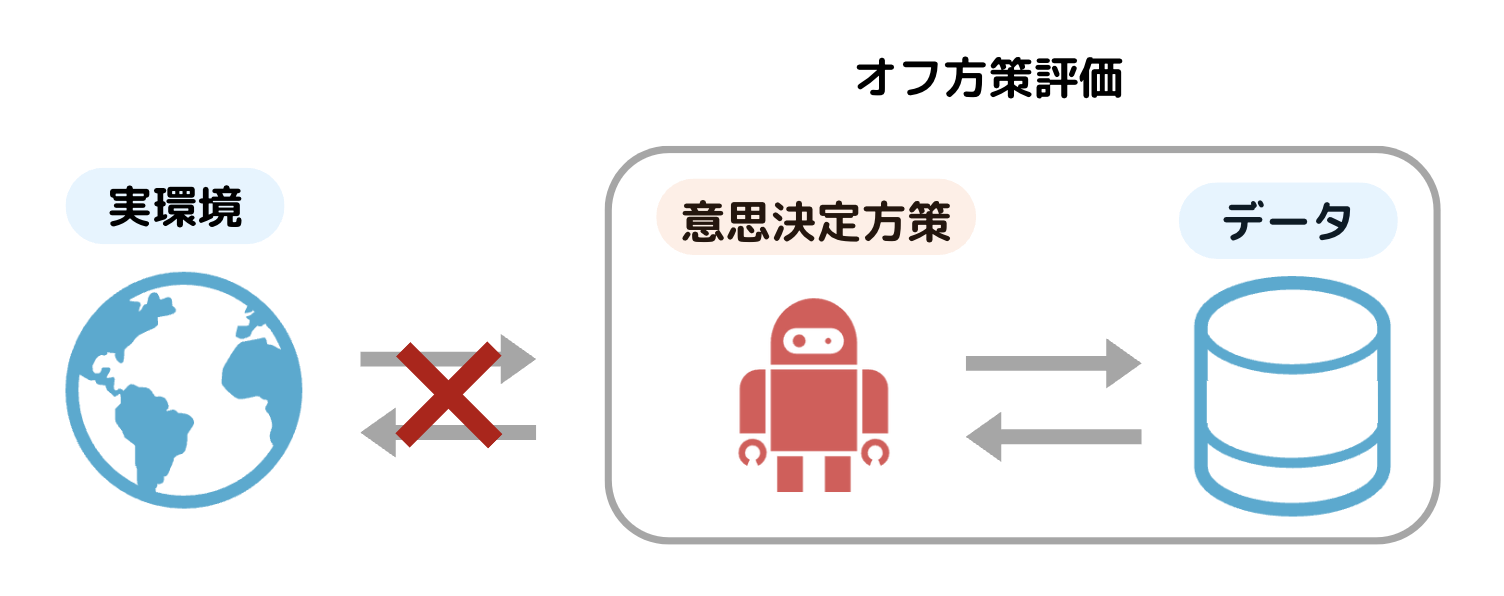
方策評価では,意思決定方策(アルゴリズムによる意思決定のルール)の性能を評価することを考えます.例えば動画推薦の例では,ユーザーに最適な動画を提案するために,改良した新しい動画推薦アルゴリズムの性能を評価することが求められます.新しい意思決定方策の性能は,実環境(オンライン環境)で試すオンライン実験 によって評価できますが,オンライン実験は多くの課題があります.例えば,仮に性能の悪い動画推薦アルゴリズムを実環境で試してしまった場合,ユーザー体験に悪影響を及ぼし,大きな損失が発生する恐れがあります.さらにはオンライン実験はそもそも実装コストがかかる他,医療や教育の現場では倫理的な観点から行えない可能性もあります.これらの問題点を解決するのが,新たな意思決定方策の価値を過去の意思決定方策から集められたデータのみを利用して評価 する オフ方策評価(OPE) です.オフ方策評価は新たな方策であったとしてもオンライン実験を行わずに性能を評価できる点で実用面から多くの注目が集まっています.
\newcommand{\mE}{\mathbb{E}}
\newcommand{\mR}{\mathbb{R}}
\newcommand{\calD}{\mathcal{D}}
\newcommand{\calA}{\mathcal{A}}
\newcommand{\calI}{\mathcal{I}}
\newcommand{\calS}{\mathcal{S}}
\newcommand{\calT}{\mathcal{T}}
\newcommand{\calP}{\mathcal{P}}
問題設定
オフ方策評価のモチベーションについて確認したところで,ここからはオフ方策評価を行う問題設定として,幅広い分野で利用可能な 連続的意思決定の最適化 を考えます.
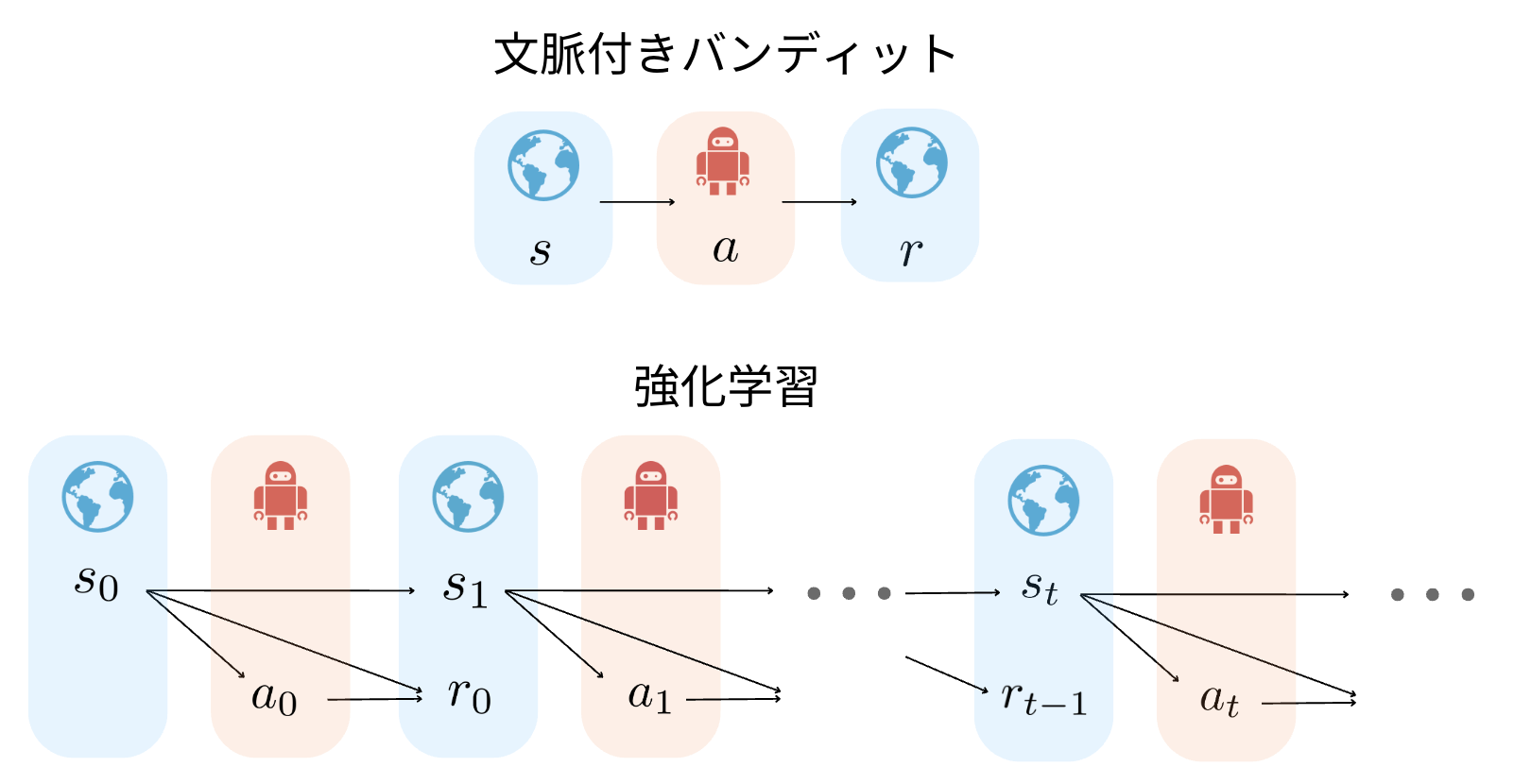
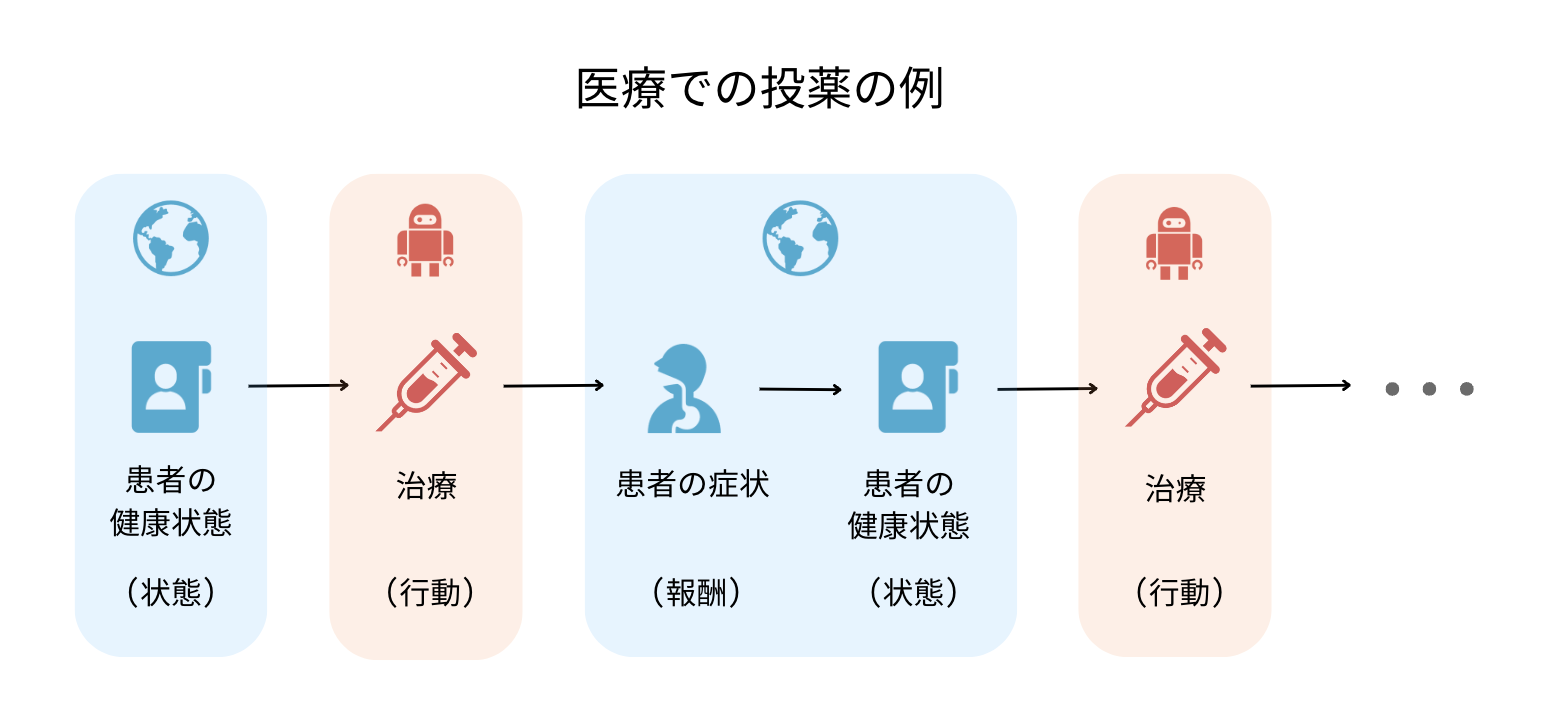
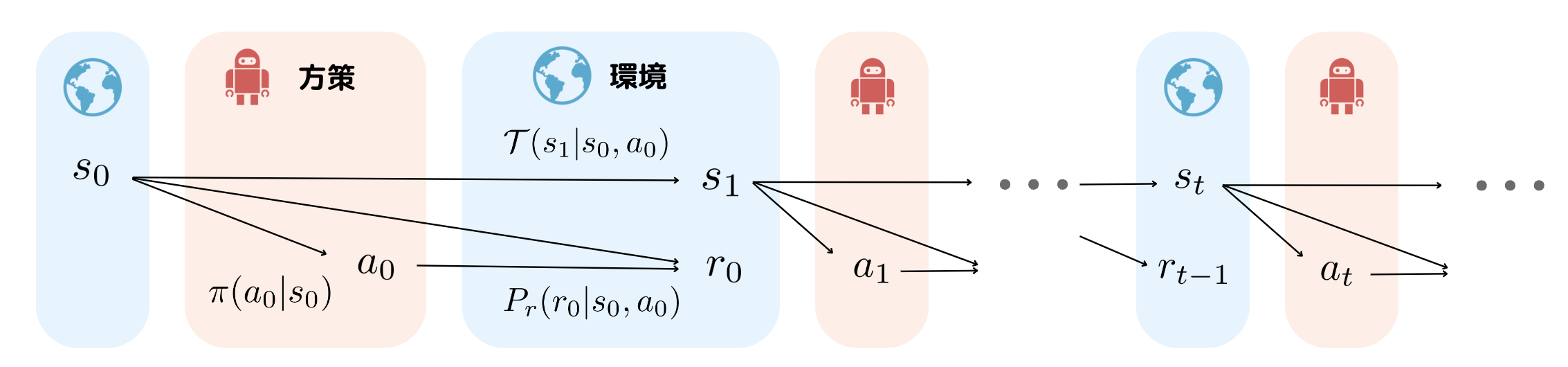
まずは身近な連続的な意思決定について,医療での投薬の例で確認します.まず患者がやってくると,患者の健康状態(熱・咳・喉の痛みなど)を確認し,それに対して意思決定方策がなんらかの治療を施します.治療を受けると,患者の症状(病気の進行度やウィルス感染状況など)と健康状態が変化します.このような流れを連続的に何度か繰り返していく意思決定は強化学習の問題として定式化でき,特にマルコフ決定過程 (MDP) と呼ばれる構造で定式化できます.
時刻$t=0$で初期状態$s_0$が観測され,状態$s_0$から方策$\pi(a_0|s_0)$によって行動$a_0$を選択します.すると報酬分布$P_r(r_0|s_0,a_0)$から報酬$r_0$が観測されるとともに,状態遷移確率$\mathcal{T}(s_{1}|s_0, a_0)$を元に状態が$s_{0}$から$s_{1}$へと遷移します.さらに状態$s_{1}$から方策が行動$a_{1}$を決定する流れを最大時刻$T-1$になるまで繰り返します.
オフ方策評価では行動を選択する方策の性能に興味があり,以下で定義される方策$\pi$の性能を評価することを考えます.
J(\pi) := \mathbb{E}_{\tau \sim p_{\pi}} \left[ \sum_{t=0}^{T-1} \gamma^t r_{t} \mid \pi \right ]
方策$\pi$の価値は割引率$\gamma$を考慮した累積報酬の期待値 として定義されており,方策$\pi$を実環境で走らせたときに得られる軌跡$\tau$について期待値を取っています.
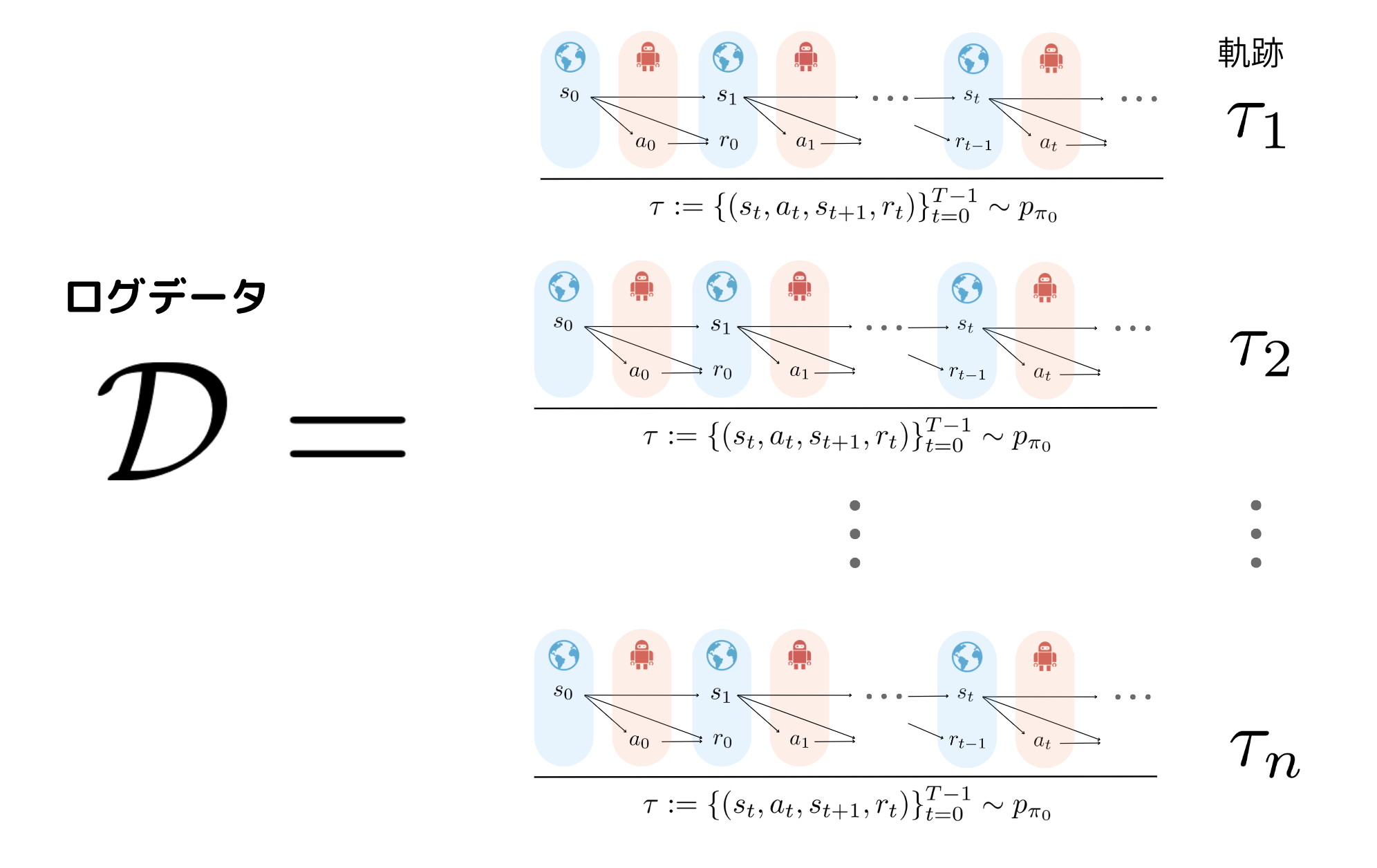
さて,オフ方策評価では上記の方策$\pi$の性能を過去に集められたログデータを用いて評価しますが,ここでオフ方策評価を行う際に重要なログデータ(過去のデータ)について確認します.
上の図のように,過去の方策$\pi_0$(以後新しい方策$\pi$と区別)による分布 $p_{\pi_0}(\cdot)$から一つの連続的な意思決定が終了するまでの履歴である軌跡$\tau$が収集され,その軌跡が$n$個集まったものが,ログデータ$\mathcal{D}$になっています.数式で表すと以下のようになります.
\tau := \{ (s_t, a_t, s_{t+1}, r_t) \}_{t=0}^{T-1} \sim p(s_0) \prod_{t=0}^{T-1} \pi_0(a_t | s_t) \mathcal{T}(s_{t+1} | s_t, a_t) P_r (r_t | s_t, a_t)
\mathcal{D}=\{\tau_i \}_{i=1}^n \sim p_{\pi_0}
さて,オフ方策評価では上記のような過去の方策$\pi_0$によって集められたログデータ$\mathcal{D}$を使って方策価値$J(\pi)$を推定します. より具体的には,オフ方策推定量$\hat{J}$とログデータ$\mathcal{D}$から新たな方策の価値を$J(\pi) \simeq \hat{J}(\pi; D)$と推定します.この推定を正確にすることがオフ方策評価の目標です.そのため推定量が正確かどうかを計る指標としては,以下で定義される平均二乗誤差(MSE) を利用します.
\begin{aligned}
\operatorname{MSE}(\hat{J}(\pi ; \mathcal{D})): & =\mathbb{E}_{\mathcal{D} \sim p_{\pi}}\left[(J(\pi)-\hat{J}(\pi ; \mathcal{D}))^2\right] \\
& = \left(J(\pi)- \mathbb{E}_{\mathcal{D} \sim p_{\pi}}\left[\hat{J}(\pi ; \mathcal{D})\right] \right) ^2 + \mathbb{E}_{\mathcal{D} \sim p_{\pi}}\left[ \left(\hat{J}(\pi ; \mathcal{D})
- \mathbb{E}_{\mathcal{D} \sim p_{\pi}}\left[\hat{J}(\pi ; \mathcal{D})\right] \right) ^2\right] \\\
& =\operatorname{Bias}(\hat{J}(\pi ; \mathcal{D}))^2+\mathbb{V}_{\mathcal{D} \sim p_{\pi}}[\hat{J}(\pi ; \mathcal{D})]
\end{aligned}
MSEは上記のように バイアス(bias) の2乗と バリアンス(variance) に分解できます.そのため,MSEを小さくするにはバイアスとバリアンスの両方を小さくすることが重要です.そこで以下では既存の推定量$\hat{J}$の良し悪しをバイアスとバリアンスの2つの性質に注目して議論します.
オフ方策評価の推定量
ここからは強化学習の設定におけるオフ方策評価の推定量を紹介し,その性質をバイアスとバリアンスの観点から,理論と簡易実験の両面で解説します.
- Direct Method 推定量 (DM)
- Trajectory-wise Importance Sampling 推定量 (TIS)
- Per-Decision Importance Sampling 推定量 (PDIS)
- Doubly Robust 推定量 (DR)
- Self-Normalized 推定量 (SNTIS,SNPDISなど)
- Marginalized Importance Sampling 推定量(MIS)
- Spectrum of Off-Policy 推定量(SOPE)
Direct Method推定量 (DM)
まずは一番基本的な推定量であるDirect Method推定量 (DM) [3-1]を説明します.オフ方策評価の目標は累積報酬で定義される方策価値を推定することでしたが,この問題を単純にするために 状態価値,行動価値を導入します.
\begin{align*}
V^{\pi}(s_t) := \mE_{\tau_{t:T-1} \sim p_{\pi}(\tau_{t:T-1}|s_t)}\left[\sum_{t'=t}^{T-1}\gamma^{t'-t}r_{t'}\right]
,\quad {Q}^{\pi}(s_t, a_t) :=\mE_{\tau_{t:T-1}\sim p_{\pi}(\tau_{t:T-1}|s_t, a_t)}\left[\sum_{t'=t}^{T-1}\gamma^{t'-t}r_{t'}\right]
\end{align*}
期待値の部分が一見難しく見えますが,状態価値 $ V^{\pi}(s_t)$は状態$s_t$を訪れる条件のもとで,将来の累積報酬の期待値を表し,行動価値 ${Q}^{\pi}(s_t, a_t)$は状態$s_t$を訪れ,行動$a_t$を選択した条件のもとで,将来の累積報酬の期待値を表しています.推定したい方策価値$J(\pi)$は$J(\pi)=\mathbb{E}_{s_0 \sim p(s_0)}[V^{\pi}(s_0)]$と書き換えることができ,方策に依存しない初期の状態分布$p(s_0)$のもとで,状態価値の期待値を測っています.そのためDMでは初期の状態価値を推定し,方策価値$J(\pi)$を求めます.
\large{\hat{J}_{\mathrm{DM}} (\pi; \mathcal{D}) := \frac{1}{n} \sum_{i=1}^n \sum_{a \in \mathcal{A}} \pi(a | s_{0}^{(i)}) \hat{Q}^{\pi}(s_{0}^{(i)}, a) = \frac{1}{n} \sum_{i=1}^n \hat{V}^{\pi}(s_{0}^{(i)})}
状態価値と行動価値の関係式は$V^{\pi}(s_t) = \sum_{a\in\mathcal{A}}\pi(a|s_t)Q^{\pi}(s_t, a)$を利用しています.すなわち,DMは初期の行動価値を推定し,推定した行動価値$\hat{Q}^{\pi}(s_0, a )$を行動について方策に基づき期待値をとることで,初期の状態価値$\hat{V}^{\pi}(s_0)$を推定します.DMの定義を理解したところで,次は重要な性質であるDMのバイアスを計算によって確認します.
\begin{align*}
\operatorname{Bias}[\hat{J}_{\mathrm{DM}}(\pi;D)] & = J(\pi)- \mathbb{E}_{s_0\sim p(s_0)}\left[\hat{V}^{\pi}(s_0)\right]\\
& = \mathbb{E}_{s_0\sim p(s_0)}\left[\sum_{a\in\cal{A}}\pi(a | s_0)Q^{\pi}(s_0, a)\right]- \mathbb{E}_{s_0\sim p(s_0)}\left[\sum_{a\in\cal{A}}\pi(a | s_0)\hat{Q}^{\pi}(s_0, a)\right]\\
& = \mathbb{E}_{s_0\sim p(s_0)}\left[\sum_{a\in\cal{A}}\pi(a | s_0)\left(Q^{\pi}(s_0, a)- \hat{Q}^{\pi}(s_0, a)\right) \right]
\end{align*}
DMは一般的にバリアンスを抑えることができる一方で,正確さが行動価値$\hat{Q}$の推定精度に大きく依存し,推定誤差$Q^{\pi}(s_0, a)- \hat{Q}^{\pi}(s_0, a)$が大きい場合は大きなバイアスが発生 します.
Trajectory-wise Importance Sampling推定量 (TIS)
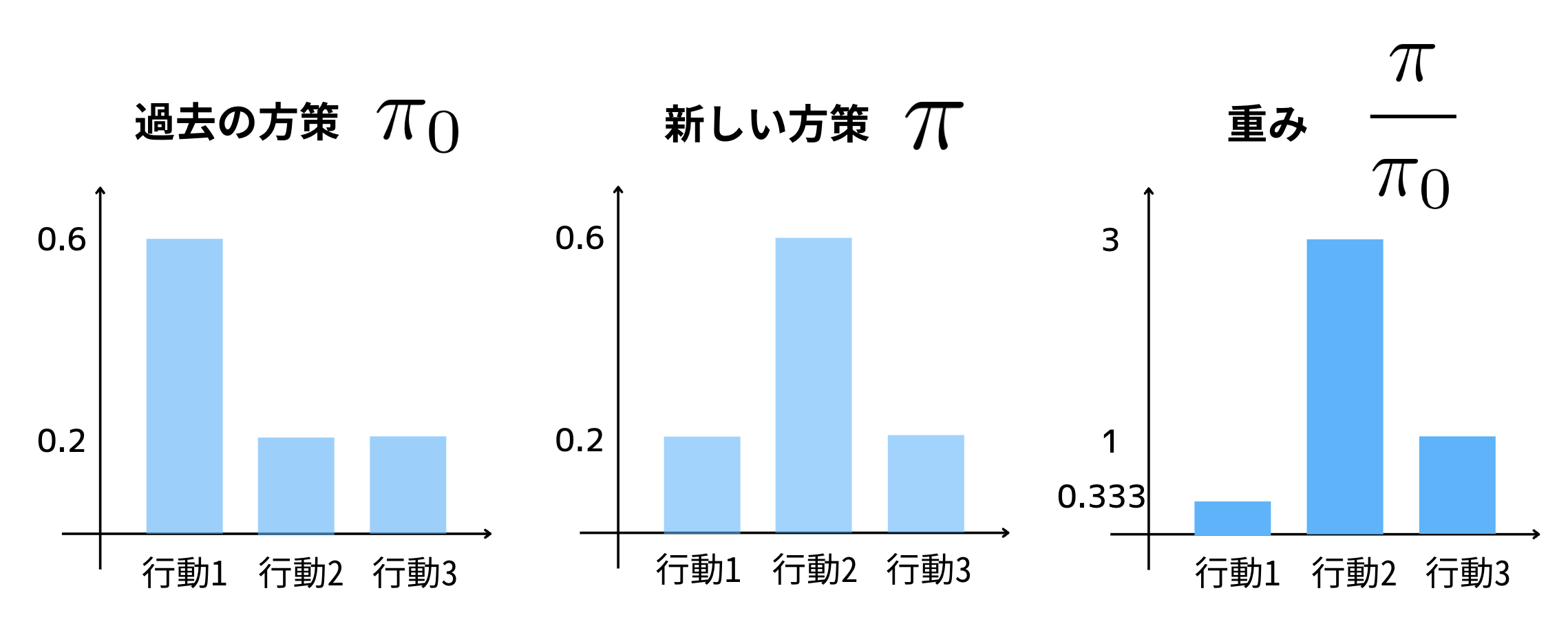
DM推定量は大きなバイアス(偏り)を持つことを紹介しましたが,次は不偏性を持つTrajectory-wise Importance Sampling推定量 (TIS) [3-2]を紹介します.TISは 重点サンプリング(Importance Sampling) を利用しています.重点サンプリングとはサンプリングされたデータに対して出現確率に応じて重みをつける手法です.
例えば上の図のように過去の方策$\pi_0$と新しい方策$\pi$で3つの行動(行動1, 行動2, 行動3)を選択する確率が定まっているとします.サンプリングされた利用可能なデータは過去の方策により集められたもので,行動1を多く選択していることがわかります.一方評価したい新しい方策では行動2を多く選択しています.新しい方策により得られる報酬を推定する際に,過去の方策により収集された報酬をそのまま利用しようとすると確率分布のズレを考慮できません.ここで,新しい方策を過去の方策で割った「重み」を考えることで,行動1のように過去の方策で過剰に集めれている行動の重みは小さくなり,逆に行動2のように新しい方策で確率が高い行動の重みは大きくなります.この重みを報酬に掛け合わせることで,過去の方策と新しい方策の間での確率分布の違いを考慮した報酬を得ることができます.この重点サンプリングを利用したTISは以下のように定義されます.
\large{\hat{J}_{\mathrm{TIS}} (\pi; \mathcal{D}) := \frac{1}{n} \sum_{i=1}^n \sum_{t=0}^{T-1} \gamma^t w_{0:T-1}^{(i)} r_t^{(i)}}
ここで$w_{0:T-1} := \prod_{t=0}^{T-1} (\pi(a_t | s_t) / \pi_0(a_t | s_t))$を 軌跡単位での重要度重み とよび,$t$期ごとでの重み$\pi(a_t | s_t) / \pi_0(a_t | s_t)$を全ての時刻($0\sim T-1$)で掛け合わせたものになっています.TISでは重点サンプリングによる軌跡単位での重要度重みを利用することで,共通サポートの仮定 のもとで不偏性が成り立ちます.
\mathbb{E}_{\tau \sim p_{\pi_0}(\tau)}[\hat{J}_{\mathrm{TIS}} (\pi; \mathcal{D})] = J(\pi)
共通サポートの仮定とは$\forall(s_0, a_0, ..., s_{T-1}, a_{T-1}) \in S^{T-1} \times A^{T-1}, \prod_{t=0}^{T-1}\pi(a_t \mid s_t) > 0 \rightarrow \prod_{t=0}^{T-1}\pi_0(a_t \mid s_t) > 0$と定義され,新しい方策が選択する可能性のある行動は,過去の方策でも選択する可能性を持っておかなければならないと言う仮定です.証明では軌跡単位での重要度重みと$p_{\pi_0}(\tau)$の期待値の部分が,見事に打ち消し合い不偏性を満たしています.
証明
\begin{align*}
&\mathbb{E}_{\tau}[\hat{J}_{\mathrm{TIS}} (\pi; \mathcal{D})]\\
&=\mathbb{E}_{\tau \sim p_{\pi_0}}\left[\sum_{t=0}^{T-1} \gamma^t w_{0:T-1} r_t \right] \\
&= \mathbb{E}_{\tau \sim p_{\pi_0}}\left[\frac{\pi(a_0|s_0)\cdots \pi(a_{T-1}|s_{T-1})}
{\pi_0(a_0|s_0)\cdots \pi_0(a_{T-1}|s_{T-1})} \sum_{t=0}^{T-1} \gamma^{t}r_t \right]\\
&= \mathbb{E}_{\tau \sim p_{\pi_0}}\left[\frac{p(s_0)\pi(a_0|s_0)P_r(r_0|s_0, a_0)\mathcal{T}(s_{1}|s_0, a_0)\cdots \pi(a_{T-1}|s_{T-1})P_r(r_{T-1}|s_{T-1}, a_{T-1})}
{p(s_0)\pi_0(a_0|s_0)P_r(r_0|s_0, a_0)\mathcal{T}(s_{1}|s_0, a_0)\cdots \pi_0(a_{T-1}|s_{T-1})P_r(r_{T-1}|s_{T-1}, a_{T-1})} \sum_{t=0}^{T-1} \gamma^{t}r_t\right]\\
&= \mathbb{E}_{\tau \sim p_{\pi_0}}\left[\frac{p_{\pi}(\tau)}{p_{\pi_0}(\tau)}\sum_{t=0}^{T-1} \gamma^{t}r_t\right]\\
&=\sum_{\tau}p_{\pi_0}(\tau)\frac{p_{\pi}(\tau)}{p_{\pi_0}(\tau)}\sum_{t=0}^{T-1} \gamma^{t}r_t\\
&=\sum_{\tau}p_{\pi}(\tau)\sum_{t=0}^{T-1} \gamma^{t}r_t\\
&= \mathbb{E}_{\tau \sim p_{\pi}}\left[\sum_{t=0}^{T-1} \gamma^{t}r_t\right]\\
&=J(\pi)
\end{align*}
ここまで推定量の期待値と真の方策価値との差であるバイアスを求めてきました.次ははもう一つの重要な指標である推定量のばらつき度合いを示すバリアンスについて見ていきます.まずはバリアンスの導出を容易にするために,TISを再帰的に表現します.
\begin{align*}
J_{\mathrm{TIS}}^{T-1-t} := w_t(w_{t+1:T-1} r_t + \gamma J_{\mathrm{TIS}}^{T-1-(t+1)})
\end{align*}
$J_{\mathrm{TIS}}^{T-1-t}$の$(T-1-t)$は時刻$t$における残りの軌跡の長さを表し, $t=T-1$の時 $J_{\mathrm{TIS}}^0 = 0$, $t=0$の時 $J_{\mathrm{TIS}}^{T-1} = J_{\mathrm{TIS}}$が成り立ちます.再帰的に表す式変形は以下を確認してください.
式変形
\begin{align*}
J_{\mathrm{TIS}}^{T-1-t} &= \sum_{t' = t}^{T-1}\gamma^{t' -t}w_{t:T-1}r_{t'}\\
&=w_{t:T}r_t + \sum_{t' = t+1}^{T-1}\gamma^{t' -t}w_{t:T-1}r_{t'}\\
&=w_t\left(w_{t+1:T-1}r_t + \sum_{t' = t+1}^{T-1}\gamma^{t' -t}w_{t+1:T-1}r_{t'}\right)\\
&=w_t\left(w_{t+1:T-1}r_t + \gamma\sum_{t' = t+1}^{T-1}\gamma^{t' -(t+1)}w_{t+1:T-1}r_{t'}\right)\\
&=w_t\left(w_{t+1:T-1}r_t + \gamma J_{\mathrm{TIS}}^{T-1-(t+1)}\right)\\
\end{align*}
再帰的に表現したことにより,求めたTISのバリアンスは以下のようになります.ここで$w_{t} := \pi(a_{t} | s_{t}) / \pi_0(a_{t} | s_{t})$ ,$\mathbb{E}_t$は次のように定義します.
\begin{align*}
\mathbb{E}_t= \mathbb{E}_{s_t, a_t, r_t}:= \mathbb{E}_{s_t, a_t, r_t}[\cdot \mid s_0, a_0, r_0, ..., s_{t-1}, a_{t-1}, r_{t-1}]
\end{align*}
\mathbb{V}_{t}[\hat{J}_{\mathrm{TIS}}^{T-1-t}(\pi; \mathcal{D})] = \mathbb{V}_t[V(s_t)] + \mathbb{E}_{s_t} \left[ \mathbb{V}_{a_t, r_t} \left [ w_tQ(s_t, a_t) \mid s_t \right] \right ] + \color{blue} {\mathbb{E}_{s_t,a_t} \left[w_t^2\mathbb{V}_{r_{t+1}}[w_{t+1:T-1}r_t]\right]}+\mathbb{E}_{s_t, a_t}\left[ w_t^2 \gamma^2\mathbb{V}_{r_{t+1}}[\hat{J}_{\mathrm{TIS}}^{T-1-(t+1)}]\right]
証明
\begin{align*}
&\mathbb{V}_{t}[\hat{J}_{\mathrm{TIS}}^{T-1-t}(\pi; \mathcal{D})]\\
&=\mathbb{E}_{t}\left[\left(\hat{J}_{\mathrm{TIS}}^{T-1-t}\right)^2\right]-\Bigl(\mathbb{E}_{t}[V(s_t)]\Bigr)^2 \\
&=\mathbb{E}_{t}\left[\left(w_t\left(w_{t+1:T-1}r_t+\gamma \hat{J}_{\mathrm{TIS}}^{T-1-(t+1)} \right)\right)^2\right]-\mathbb{E}_{t}[V(s_t)^2]+\mathbb{V}_t[V(s_t)]\\
&=\mathbb{E}_{t}\left[\left(w_tQ(s_t, a_t)+w_t\left(w_{t+1:T-1}r_t+\gamma \hat{J}_{\mathrm{TIS}}^{T-1-(t+1)}-Q(s_t, a_t)\right)\right)^2-V(s_t)^2\right]+\mathbb{V}_{t}[V(s_t)]\\
&=\mathbb{E}_{t}\left[\left(w_tQ(s_t, a_t)+w_t\left(w_{t+1:T-1}r_t-R(s_t, a_t)\right)+w_t\gamma \left(\hat{J}_{\mathrm{TIS}}^{T-1-(t+1)} -\mathbb{E}_{s_{t+1}}[V(s_{t+1})]\right)\right)^2 -V(s_t)^2\right]+\mathbb{V}_{t}[V(s_t)]\because Q(s_t, a_t) = R(s_t, a_t) + \mathbb{E}_{s_{t+1}}\left[\gamma V(s_{t+1})\right]\\
&=\mathbb{E}_{s_t, a_t}\left[\mathbb{E}_{r_t}\left[
\left(w_tQ(s_t, a_t)+w_t\left(w_{t+1:T-1}r_t-R(s_t, a_t)\right)+w_t\gamma \left(\hat{J}_{\mathrm{TIS}}^{T-1-(t+1)} -\mathbb{E}_{s_{t+1}}[V(s_{t+1})]\right)\right)^2 -V(s_t)^2\right] \biggm\vert s_t, a_t\right]+\mathbb{V}_{t}[V(s_t)]\\
&=\mathbb{E}_{s_t}\left[\mathbb{E}_{a_t, r_t}\left[
\left(w_tQ(s_t, a_t)\right)^2 - V(s_t)^2 \mid s_t\right]\right]+\mathbb{E}_{s_t, a_t}\left[\mathbb{E}_{r_{t+1}}\left[w_{t}^2\left(w_{t+1:T-1}r_t -R(s_t, a_t)\right)^2\right]\right]\\
&+\mathbb{E}_{s_t, a_t}\left[\mathbb{E}_{r_{t+1}}\left[w_t^2\gamma^2\left(\hat{J}_{\mathrm{TIS}}^{T-1-(t+1)}-\mathbb{E}_{s_{t+1}}[V(s_{t+1})]\right)^2\right]\right]+\mathbb{V}_{t}[V(s_t)] \because w_tQ(s_t, a_t) \perp w_t\left(w_{t+1:T-1}r_t-R(s_t, a_t)\right) \perp w_t\gamma \left(\hat{J}_{\mathrm{TIS}}^{T-1-(t+1)} -\mathbb{E}_{s_{t+1}}[V(s_{t+1})]\right) \Biggm\vert s_t, a_t\\
&=\mathbb{E}_{s_t} \left[ \mathbb{V}_{a_t, r_t} \left [ w_tQ(s_t, a_t) \mid s_t \right] \right ] + \mathbb{E}_{s_t,a_t} \left[w_t^2\mathbb{V}_{r_{t+1}}[w_{t+1:T-1}r_t]\right]+\mathbb{E}_{s_t, a_t}\left[ w_t^2 \gamma^2\mathbb{V}_{r_{t+1}}[\hat{J}_{\mathrm{TIS}}^{T-1-(t+1)}]\right]+ \mathbb{V}_t[V(s_t)]\\
\end{align*}
DM vs TIS (バイアスとバリアンスのトレードオフ)
先ほどまでで理論的にDMはバリアンスは小さいものの,バイアスが大きくなる傾向があり,TISは不偏性を持つものの,バリアンスが大きくなる傾向があることを説明しました.ここでは簡易実験でそれぞれの性質を確認します.
まずは実験の前に経験的なバイアス推定 に関して説明します.本来バイアスは$\operatorname{Bias}(\hat{J}(\pi ; \mathcal{D})) = \mathbb{E}\left[ \sum_{t=0}^{T-1} \gamma^t r_{t} \mid \pi \right ] - \mathbb{E}\left[\hat{J}(\pi ; \mathcal{D})\right]$によって求まりますが,$p_{\pi}$から生成される軌跡$\tau$によって期待値を取るのは現実には困難であるため,実験では代わりに経験的なバイアスを求めることになります.経験的なバイアスとは真のバイアスを実験的に近似したものであり,真の方策価値$\mathbb{E}\left[ \sum_{t=0}^{T-1} \gamma^t r_{t} \mid \pi \right ] $を$\sum_{i=1}^n\sum_{t=0}^{T-1}\gamma^tr_t^{(i)} $で,推定価値の期待値$\mathbb{E}\left[\hat{J}(\pi ; \mathcal{D})\right]$を$ \sum_{i=1}^n \hat{J}(\pi;\tau_i)$によってサンプル近似します.実験ではこの経験的なバイアスを利用することになるため,しばしば実験結果と理論解析の結果とは異なりますが,十分に大きい実験の試行回数の元では,バイアスをある程度正確に見ることができます.
それでは経験的なバイアスを踏まえてDMとTISの比較を見てみましょう.軌跡(trajectory)の数$n$を変化させた場合のバイアス,バリアンス,MSEを比較した結果を示しています.実験ではバリアンスとのスケールを合わせるためバイアスの代わりにバイアスの2乘を利用します.
DMは大きなバイアスが発生していますが,TISは不偏性が成り立っていることがみて取れます.一方バリアンスも理論と同じ結果が実験で確認でき,DMはほとんど発生していない一方で,TISは大きなバリアンスが発生しています.MSEはデータ数が小さい場合はDMが優れていますが,データ数が増えるごとにTISのバリアンスが小さくなるためTISが優位になります.
DM vs TIS (Curse of Horizon)
次は軌跡の長さ$T$を変化させた場合のDMとTISの比較を調べた結果を示しています.縦軸は先ほどと違いlogスケールになっている点に注意してください.
TISのバリアンスは軌跡が長くなるごとに指数関数的に大きくなってしまっています.このように軌跡が長くなった場合に指数関数的なバリアンスを持ってしまう現象 は,研究コミュニティではCurse of Horizon として認知されており,非常に厄介な問題点となります.
ここまでDMとTISの2つの推定量を見てきましたが,これらは最も基礎的な推定量であり工夫の余地が多く残っています.特にTISのバイアスに関して良い性質を持ったまま,いかに問題点であるバリアンスを抑えることができるかが研究され,改良した推定量が提案されています.
Per-Decision Importance Sampling推定量 (PDIS)
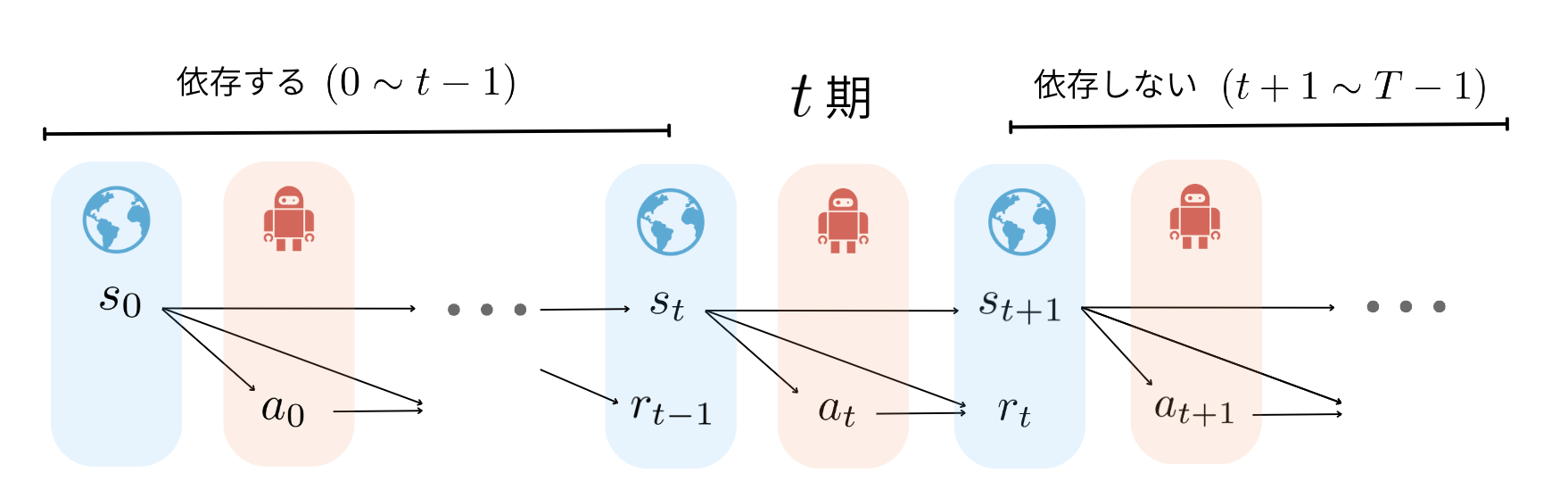
そもそもTISでは$0 \sim T-1$期の全てを重要度重みとして考慮していたことでバリアンスがより大きくなっていました.そこでMDPの性質を利用してTISの重要度重みを改良しようとしたのがPer-Decision Importance Sampling推定量 (PDIS) [3-2]です.MDPでは下の図のように逐次的な意思決定を行うため,$s_t$は$s_0, ... ,s_{t-1}$や$a_0, ...,a_{t-1}$にのみ依存し,$s_{t+1}, ... ,s_{T-1}$や$a_{t+1}, ...,a_{T-1}$に依存しません.
つまりPDISでは$t$期の報酬を推定する際に依存している部分である過去$0, ..., t$の重要度重みのみを考慮することで,バリアンスを抑えようとする推定量として提案されています.
\large{\hat{J}_{\mathrm{PDIS}} (\pi; \mathcal{D}) := \frac{1}{n} \sum_{i=1}^n \sum_{t=0}^{T-1} \gamma^t w_{0:t}^{(i)} r_t^{(i)}}
$w_{0:t} := \prod_{t'=0}^t (\pi(a_{t'} | s_{t'}) / \pi_0(a_{t'} | s_{t'}))$で表され,意思決定単位での重要度重み と呼びます.MDPの性質を利用し重要度重みの積を軽減しつつ,共通サポートの仮定のもとで不偏推定量となるTISの性質を保っている点がPDISの利点になります.
\mathbb{E}_{\tau \sim p_{\pi_0}}[\hat{J}_{\mathrm{PDIS}} (\pi; \mathcal{D})] = J(\pi)
MDPの性質をうまく利用することで不偏性を満たします.(証明参照)
証明
\begin{align*}
\mathbb{E}_{\tau}[\hat{J}_{\mathrm{PDIS}} (\pi; \mathcal{D})]
&= \mathbb{E}_{\tau \sim p_{\pi_0}}\left[\sum_{t=0}^{T-1}\frac{\pi(a_0|s_0)\cdots \pi(a_{t}|s_{t})}
{\pi_0(a_0|s_0)\cdots \pi_0(a_{t}|s_{t})} \gamma^{t}r_t \right]\\
&= \sum_{t=0}^{T-1} \mathbb{E}_{\tau \sim p_{\pi_0}} \left[ \frac{\pi(a_0|s_0)\cdots \pi(a_{t}|s_{t})}
{\pi_0(a_0|s_0)\cdots \pi_0(a_{t}|s_{t})} \gamma^{t}r_t \right] \\
&= \sum_{t=0}^{T-1} \mathbb{E}_{\tau \sim p_{\pi_0}}\left[\frac{\pi(a_0|s_0)\cdots \pi(a_{t}|s_{t})}
{\pi_0(a_0|s_0)\cdots \pi_0(a_{t}|s_{t})} \gamma^{t}r_t \right]
\underbrace{\mathbb{E}_{\pi_0(a_0|s_0)\cdots\pi_0(a_t|s_t)}\left[\sum_{a_{t+1}}\cdots\sum_{a_{T-1}}\pi(a_{t+1}|s_{t+1})\cdots\pi(a_{T-1}|s_{T-1})\right]}_{=1} \\
&= \sum_{t=0}^{T-1} \mathbb{E}_{\tau \sim p_{\pi_0}}\left[\frac{\pi(a_0|s_0)\cdots \pi(a_{t}|s_{t})}
{\pi_0(a_0|s_0)\cdots \pi_0(a_{t}|s_{t})} \gamma^{t}r_t \right]
\mathbb{E}_{\tau \sim p_{\pi_0}}\left[\frac{\pi(a_{t+1}|s_{t+1})\cdots \pi(a_{T-1}|s_{T-1})}
{\pi_0(a_{t+1}|s_{t+1})\cdots \pi_0(a_{T-1}|s_{T-1})}\right]\\
&= \mathbb{E}_{\tau \sim p_{\pi_0}}\left[\sum_{t=0}^{T-1}\frac{\pi(a_0|s_0)\cdots \pi(a_{T-1}|s_{T-1})}
{\pi_0(a_0|s_0)\cdots \pi_0(a_{T-1}|s_{T-1})} \gamma^{t}r_t \right]\\
&= \mathbb{E}_{\tau \sim p_{\pi_0}}\left[\frac{p_{\pi}(\tau)}{p_{\pi_0}(\tau)}\sum_{t=0}^{T-1} \gamma^{t}r_t\right]\\
&= \mathbb{E}_{\tau \sim p_{\pi}}\left[\sum_{t=0}^{T-1} \gamma^{t}r_t\right]\\
&=J(\pi)
\end{align*}
先ほどと同様にバリアンスを求めるため,PDISを再帰的に表します.$J_{\mathrm{PDIS}}^0 = 0,J_{\mathrm{PDIS}}^{T-1} = J_{\mathrm{PDIS}}$が成り立ちます.
\begin{align*}
J_{\mathrm{PDIS}}^{T-1-t} := w_t(r_t + \gamma J_{\mathrm{PDIS}}^{T-1-(t+1)})
\end{align*}
式変形
\begin{align*}
J_{\mathrm{PDIS}}^{T-1-t} &= \sum_{t' = t}^{T-1}\gamma^{t' -t}w_{t:t'}r_{t'}\\
&=w_tr_t + \sum_{t' = t+1}^{T-1}\gamma^{t' -t}w_{t:t'}r_{t'}\\
&=w_t\left(r_t + \sum_{t' = t+1}^{T-1}\gamma^{t' -t}w_{t+1:t'}r_{t'}\right)\\
&=w_t\left(r_t + \gamma\sum_{t' = t+1}^{T-1}\gamma^{t' -(t+1)}w_{t+1:t'}r_{t'}\right)\\
&=w_t(r_t + \gamma J_{\mathrm{PDIS}}^{T-1-(t+1)})\\
\end{align*}
PDISのバリアンスを計算すると以下のようになります.
\mathbb{V}_{t}[\hat{J}_{\mathrm{PDIS}}^{T-1-t}(\pi; \mathcal{D})] = \mathbb{V}_t[V(s_t)] +\mathbb{E}_{s_t} \left[ \mathbb{V}_{a_t, r_t} \left [ w_tQ(s_t, a_t) \mid s_t \right] \right ] + \mathbb{E}_{s_t,a_t} \left[w_t^2\color{blue} {\mathbb{V}_{r_{t+1}}[r_t]}\right] +\mathbb{E}_{s_t, a_t}\left[ w_t^2 \gamma^2\mathbb{V}_{r_{t+1}}[\hat{J}_{\mathrm{PDIS}}^{T-1-(t+1)}]\right]
証明
\begin{align*}
&\mathbb{V}_{t}[\hat{J}_{\mathrm{PDIS}}^{T-1-t}(\pi; \mathcal{D})]\\
&=\mathbb{E}_{t}\left[\left(\hat{J}_{\mathrm{PDIS}}^{T-1-t}\right)^2\right]-\Bigl(\mathbb{E}_{t}[V(s_t)]\Bigr)^2 \\
&=\mathbb{E}_{t}\left[\left(w_t\left(r_t+\gamma \hat{J}_{\mathrm{PDIS}}^{T-1-(t+1)} \right)\right)^2\right]-\mathbb{E}_{t}[V(s_t)^2]+\mathbb{V}_t[V(s_t)]\\
&=\mathbb{E}_{t}\left[\left(w_tQ(s_t, a_t)+w_t\left(r_t+\gamma \hat{J}_{\mathrm{PDIS}}^{T-1-(t+1)}-Q(s_t, a_t)\right)\right)^2-V(s_t)^2\right]+\mathbb{V}_{t}[V(s_t)]\\
&=\mathbb{E}_{t}\left[\left(w_tQ(s_t, a_t)+w_t\left(r_t-R(s_t, a_t)\right)+w_t\gamma \left(\hat{J}_{\mathrm{PDIS}}^{T-1-(t+1)} -\mathbb{E}_{s_{t+1}}[V(s_{t+1})]\right)\right)^2 -V(s_t)^2\right]+\mathbb{V}_{t}[V(s_t)]\because Q(s_t, a_t) = R(s_t, a_t) + \mathbb{E}_{s_{t+1}}\left[\gamma V(s_{t+1})\right]\\
&=\mathbb{E}_{s_t, a_t}\left[\mathbb{E}_{r_t}\left[
\left(w_tQ(s_t, a_t)+w_t\left(r_t-R(s_t, a_t)\right)+w_t\gamma \left(\hat{J}_{\mathrm{PDIS}}^{T-1-(t+1)} -\mathbb{E}_{s_{t+1}}[V(s_{t+1})]\right)\right)^2 -V(s_t)^2\right] \biggm\vert s_t, a_t\right]+\mathbb{V}_{t}[V(s_t)]\\
&=\mathbb{E}_{s_t}\left[\mathbb{E}_{a_t, r_t}\left[
\left(w_tQ(s_t, a_t)\right)^2 - V(s_t)^2 \mid s_t\right]\right]+\mathbb{E}_{s_t, a_t}\left[\mathbb{E}_{r_{t+1}}\left[w_{t}^2\left(r_t -R(s_t, a_t)\right)^2\right]\right]\\
&+\mathbb{E}_{s_t, a_t}\left[\mathbb{E}_{r_{t+1}}\left[w_t^2\gamma^2\left(\hat{J}_{\mathrm{PDIS}}^{T-1-(t-1)}-\mathbb{E}_{s_{t+1}}[V(s_{t+1})]\right)^2\right]\right]+\mathbb{V}_{t}[V(s_t)]\because w_tQ(s_t, a_t) \perp w_t\left(r_t-R(s_t, a_t)\right) \perp w_t\gamma \left(\hat{J}_{\mathrm{PDIS}}^{T-1-(t+1)} -\mathbb{E}_{s_{t+1}}[V(s_{t+1})]\right) \Biggm\vert s_t, a_t\\
&=\mathbb{E}_{s_t} \left[ \mathbb{V}_{a_t, r_t} \left [ w_tQ(s_t, a_t) \mid s_t \right] \right ] + \mathbb{E}_{s_t,a_t} \left[w_t^2\mathbb{V}_{r_{t+1}}[r_t]\right]+\mathbb{E}_{s_t, a_t}\left[ w_t^2 \gamma^2\mathbb{V}_{r_{t+1}}[\hat{J}_{\mathrm{PDIS}}^{T-1-(t+1)}]\right]+ \mathbb{V}_t[V(s_t)]\\
\end{align*}
TISのバリアンス(再掲)
\mathbb{V}_{t}[\hat{J}_{\mathrm{TIS}}^{T-1-t}(\pi; \mathcal{D})] = \mathbb{V}_t[V(s_t)] + \mathbb{E}_{s_t} \left[ \mathbb{V}_{a_t, r_t} \left [ w_tQ(s_t, a_t) \mid s_t \right] \right ] + \mathbb{E}_{s_t,a_t} \left[w_t^2\color{blue} {\mathbb{V}_{r_{t+1}}[w_{t+1:T-1}r_t]}\right] + \mathbb{E}_{s_t, a_t}\left[ w_t^2 \gamma^2\mathbb{V}_{r_{t+1}}[\hat{J}_{\mathrm{TIS}}^{T-1-(t+1)}]\right]
先ほど求めたTISのバリアンスと比較すると,PDISの工夫した点が浮かび上がってきます.第3項のみ異なっており,PDISはTISでの$r_t$の係数$w_{t+1:T-1}$が除かれていることがわかります.PDISはこの将来の重要度重みの積$w_{t+1:T-1}$の分だけTISよりもバリアンスが小さくなります.つまりPDISでは 軌跡単位での重要度重みから意思決定単位での重要度重みに変えたことによってバリアンスを抑えています .
TIS vs PDIS
TISとそれを改良したPDISに関して,軌跡の長さ$T$を変化させた場合の結果を示しています.
PDISはバイアスをTISと同等に保ちつつも(logスケールを考慮するとバリアンスに比べればバイアスの差は微小),バリアンスを大幅に抑えられていることが見て取れます.したがってMSEを見ても分かるようにDMとTISようなトレードオフの関係にあるわけではなく,PDISはTISよりも優れた推定量であると言えます.しかしたとえPDISであったとしても,軌跡の長さ$T$が大きい場合は依然としてバリアンスが大きくなってしまいます.
Doubly Robust推定量 (DR)
バリアンスに強いDMとバイアスに強いPDISを組み合わせた推定量としてDoubly Robust推定量 (DR)[3-3]が提案されています.DRではうまくPDISとDMを組み合わせるために,再帰的に表現されたPDISにDMで利用した行動価値の推定$\hat{Q}$をベースラインとして組み込みます.
\begin{align*}
J_{\mathrm{DR}}^{T-1-t} := \sum_{a\in \calA}\pi(a|s_t)\hat{Q}(s_t, a) + w_t(r_t + \gamma J_{\mathrm{DR}}^{T-1-(t+1)} - \hat{Q}(s_t, a_t))
\end{align*}
このように定義された再帰的なDRを元の形に戻した以下のDRが提案されます.
式変形
\begin{align*}
J_{\mathrm{DR}}^{T-1-0} &= \sum_{a\in \calA}\pi(a|s_0)\hat{Q}(s_0, a) + w_0(r_0 + \gamma J_{\mathrm{DR}}^{T-1-1} - \hat{Q}(s_0, a_0))\\
&= \sum_{a\in \calA}\pi(a|s_0)\hat{Q}(s_0, a) + w_0(r_0 - \hat{Q}(s_0, a_0)) + w_0 \gamma \left(\sum_{a\in \calA}\pi(a|s_{1})\hat{Q}(s_{1}, a) + w_{1}(r_{1} + \gamma J_{\mathrm{DR}}^{T-1-2} - \hat{Q}(s_1, a_1))\right)\\
&= \sum_{a\in \calA}\pi(a|s_0)\hat{Q}(s_0, a) + w_0\gamma\sum_{a\in \calA}\pi(a|s_1)\hat{Q}(s_1, a) + w_0(r_0 -\hat{Q}(s_0, a_0)) + w_{0:1} \gamma (r_{1} - \hat{Q}(s_1, a_1)) + w_{0:1} \gamma J_{\mathrm{DR}}^{T-1-2}\\
& \quad \quad \vdots\\
&=\sum_{t=0}^{T-1} \gamma^tw_{0:t-1}\sum_{a \in \mathcal{A}} \pi(a | s_t) \hat{Q}(s_t, a) + \sum_{t=0}^{T-1} \gamma^t w_{0:t} (r_t - \hat{Q}(s_t, a_t)) \\
&=\sum_{t=0}^{T-1} \gamma^t \left(w_{0:t} (r_t - \hat{Q}(s_t, a_t)) + w_{0:t-1}\sum_{a \in \mathcal{A}} \pi(a | s_t) \hat{Q}(s_t, a) \right)\\
\end{align*}
\large{\hat{J}_{\mathrm{DR}} (\pi; \mathcal{D})
:= \frac{1}{n} \sum_{i=1}^n \sum_{t=0}^{T-1} \gamma^t \left(w_{0:t}^{(i)} (r_t^{(i)} - \hat{Q}(s_t^{(i)}, a_t^{(i)})) + w_{0:t-1}^{(i)} \sum_{a \in \mathcal{A}} \pi(a | s_t^{(i)}) \hat{Q}(s_t^{(i)}, a) \right)}
DRはPDISの性質を引き継ぎ,共通サポートの仮定のもとで不偏性を持ちます.
\mathbb{E}_{\tau \sim p_{\pi_0}}[\hat{J}_{\mathrm{DR}} (\pi; \mathcal{D})] = J(\pi)
証明では$p_{\pi_0}(\tau)$の期待値を取ることで組み込んだベースライン$\hat{Q}$がうまく打ち消され,PDISと同じように不偏推定量となります.
証明
\begin{align*}
&\mathbb{E}_{\tau}[\hat{J}_{\mathrm{DR}} (\pi; \mathcal{D})]\\
&= \mathbb{E}_{\tau \sim p_{\pi_0}} \left[\sum_{t=0}^{T-1} \gamma^t \left (w_{0:t} (r_t - \hat{Q}(s_t, a_t)) + w_{0:t-1} \mathbb{E}_{a \sim \pi(a | s_t)}[\hat{Q}(s_t, a)]\right)\right]\\
&= \mathbb{E}_{\tau \sim p_{\pi_0}}[\hat{J}_{\mathrm{PDIS}} (\pi; \mathcal{D})] - \mathbb{E}_{\tau \sim p_{\pi_0}} \left[\sum_{t=0}^{T-1} \gamma^t w_{0:t}\hat{Q}(s_t, a_t) \right] + \mathbb{E}_{\tau \sim p_{\pi_0}} \left[\sum_{t=0}^{T-1} \gamma^t w_{0:t-1} \mathbb{E}_{a \sim \pi_0(a | s_t)}\left[\frac{\pi(a \mid s_t)}{\pi_0(a \mid s_t)}\hat{Q}(s_t, a)\right]\right]\\
&= \mathbb{E}_{\tau \sim p_{\pi_0}}[\hat{J}_{\mathrm{PDIS}} (\pi; \mathcal{D})] - \mathbb{E}_{\tau \sim p_{\pi_0}} \left[\sum_{t=0}^{T-1} \gamma^t w_{0:t}\hat{Q}(s_t, a_t) \right] + \mathbb{E}_{\tau \sim {p(s_0) \prod_{t=0}^{T-1} \pi_0(a_t | s_t) \mathcal{T}(s_{t+1} | s_t, a_t) P_r (r_t | s_t, a_t)}} \left [\sum_{t=0}^{T-1} \gamma^t w_{0:t-1} \mathbb{E}_{a \sim \pi_0(a | s_t)}\left[\frac{\pi(a \mid s_t)}{\pi_0(a \mid s_t)}\hat{Q}(s_t, a)\right]\right]\\
&= \mathbb{E}_{\tau \sim p_{\pi_0}}[\hat{J}_{\mathrm{PDIS}} (\pi; \mathcal{D})] - \mathbb{E}_{\tau \sim p_{\pi_0}} \left[\sum_{t=0}^{T-1} \gamma^t w_{0:t}\hat{Q}(s_t, a_t) \right] + \mathbb{E}_{\tau \sim { p(s_0) \prod_{t=0}^{T-1} \pi_0(a_t | s_t) \mathcal{T}(s_{t+1} | s_t, a_t) P_r (r_t | s_t, a_t)}} \left [\sum_{t=0}^{T-1} \gamma^t w_{0:t-1} \frac{\pi(a_t \mid s_t)}{\pi_0(a_t \mid s_t)}\hat{Q}(s_t, a_t)\right]\\
&= \mathbb{E}_{\tau \sim p_{\pi_0}}[\hat{J}_{\mathrm{PDIS}} (\pi; \mathcal{D})] - \mathbb{E}_{\tau \sim p_{\pi_0}} \left[\sum_{t=0}^{T-1} \gamma^t w_{0:t}\hat{Q}(s_t, a_t) \right] + \mathbb{E}_{\tau \sim p_{\pi_0}} \left[\sum_{t=0}^{T-1} \gamma^t w_{0:t}\hat{Q}(s_t, a_t) \right] \\
&= J(\pi)
\end{align*}
\mathbb{V}_{t}[\hat{J}_{\mathrm{DR}}^{T-1-t}(\pi; \mathcal{D})] = \mathbb{V}_t[V(s_t)]+ \mathbb{E}_{s_t}\left[\mathbb{V}_{a_t, r_t}\left[w_t\color{blue} {(\hat{Q}(s_t, a_t)-Q(s_t, a_t)) }\mid s_t\right]\right]+\mathbb{E}_{s_t, a_t}\left[{w_t}^2\mathbb{V}_{r_{t+1}}[r_t]\right] + \mathbb{E}_{s_t, a_t}\left[\gamma^2{w_t}^2\mathbb{V}_{r_{t+1}}[\hat{J}_{\mathrm{DR}}^{T-1-(t+1)}]\right]
証明
\begin{align*}
&\mathbb{V}_{t}[\hat{J}_{\mathrm{DR}}^{T-1-t}(\pi; \mathcal{D})]\\
&=\mathbb{E}_{t}\left[\left(\hat{J}_{\mathrm{DR}}^{T-1-t}\right)^2\right]-\Bigl(\mathbb{E}_{t}[V(s_t)]\Bigr)^2 \\
&=\mathbb{E}_{t}\left[\left(\hat{V}(s_t)+w_t\left(r_t+\gamma \hat{J}_{\mathrm{DR}}^{T-1-(t+1)} - \hat{Q}(s_t, a_t)\right)\right)^2\right]-\mathbb{E}_{t}[V(s_t)^2]+\mathbb{V}_t[V(s_t)]\\
&=\mathbb{E}_{t}\left[\left(w_tQ(s_t, a_t)-w_t\hat{Q}(s_t, a_t)+\hat{V}(s_t)+w_t\left(r_t+\gamma \hat{J}_{\mathrm{DR}}^{T-1-(t+1)}-Q(s_t, a_t)\right)\right)^2-V(s_t)^2\right]+\mathbb{V}_{t}[V(s_t)]\\
&=\mathbb{E}_{t}\left[\left(w_t(Q(s_t, a_t)-\hat{Q}(s_t, a_t))+\hat{V}(s_t)+w_t\left(r_t-R(s_t, a_t)\right)+w_t\gamma \left(\hat{J}_{\mathrm{DR}}^{T-1-(t+1)} -\mathbb{E}_{s_{t+1}}[V(s_{t+1})]\right)\right)^2 -V(s_t)^2\right]+\mathbb{V}_{t}[V(s_t)]\because Q(s_t, a_t) = R(s_t, a_t) + \mathbb{E}_{s_{t+1}}\left[\gamma V(s_{t+1})\right]\\
&=\mathbb{E}_{s_t, a_t}\left[\mathbb{E}_{r_t}\left[
\left(w_t(Q(s_t, a_t)-\hat{Q}(s_t, a_t))+\hat{V}(s_t)+w_t\left(r_t-R(s_t, a_t)\right)+w_t\gamma \left(\hat{J}_{\mathrm{DR}}^{T-1-(t+1)} -\mathbb{E}_{s_{t+1}}[V(s_{t+1})]\right)\right)^2 -V(s_t)^2\right] \biggm\vert s_t, a_t\right]+\mathbb{V}_{t}[V(s_t)]\\
&=\mathbb{E}_{s_t}\left[\mathbb{E}_{a_t, r_t}\left[
\left(-w_t(Q(s_t, a_t)-\hat{Q}(s_t, a_t))+\hat{V}(s_t)\right)^2 - V(s_t)^2 \mid s_t\right]\right]+\mathbb{E}_{s_t, a_t}\left[\mathbb{E}_{r_{t+1}}\left[w_{t}^2\left(r_t -R(s_t, a_t)\right)^2\right]\right]\\
&+\mathbb{E}_{s_t, a_t}\left[\mathbb{E}_{r_{t+1}}\left[w_t^2\gamma^2\left(\hat{J}_{\mathrm{DR}}^{T-1-(t+1)}-\mathbb{E}_{s_{t+1}}[V(s_{t+1})]\right)^2\right]\right]+\mathbb{V}_{t}[V(s_t)]\because -w_t(Q(s_t, a_t)-\hat{Q}(s_t, a_t)) \perp w_t\left(r_t-R(s_t, a_t)\right) \perp w_t\gamma \left(\hat{J}_{\mathrm{DR}}^{T-1-(t+1)} -\mathbb{E}_{s_{t+1}}[V(s_{t+1})]\right) \Biggm\vert s_t, a_t\\
&=\mathbb{E}_{s_t} \left[ \mathbb{V}_{a_t, r_t} \left [ -w_t(Q(s_t, a_t)-\hat{Q}(s_t, a_t))+\hat{V}(s_t) \mid s_t \right] \right ] + \mathbb{E}_{s_t,a_t} \left[w_t^2\mathbb{V}_{r_{t+1}}[r_t]\right]+\mathbb{E}_{s_t, a_t}\left[ w_t^2 \gamma^2\mathbb{V}_{r_{t+1}}[\hat{J}_{\mathrm{DR}}^{T-1-(t+1)}]\right]+ \mathbb{V}_t[V(s_t)]\\
&=\mathbb{E}_{s_t}\left[\mathbb{V}_{a_t, r_t}\left[w_t(\hat{Q}(s_t, a_t)-Q(s_t, a_t)) \mid s_t\right]\right]+\mathbb{E}_{s_t, a_t}\left[{w_t}^2\mathbb{V}_{r_{t+1}}[r_t]\right] + \mathbb{E}_{s_t, a_t}\left[\gamma^2{w_t}^2\mathbb{V}_{r_{t+1}}[\hat{J}_{\mathrm{DR}}^{T-1-(t+1)}]\right] + \mathbb{V}_t[V(s_t)]
\end{align*}
PDISのバリアンス(再掲)
\mathbb{V}_{t}[\hat{J}_{\mathrm{PDIS}}^{T-1-t}(\pi; \mathcal{D})] = \mathbb{V}_t[V(s_t)] +\mathbb{E}_{s_t} \left[ \mathbb{V}_{a_t, r_t} \left [ w_t\color{blue} {Q(s_t, a_t)} \mid s_t \right] \right ] + \mathbb{E}_{s_t,a_t} \left[w_t^2\mathbb{V}_{r_{t+1}}[r_t]\right]+\mathbb{E}_{s_t, a_t}\left[ w_t^2 \gamma^2\mathbb{V}_{r_{t+1}}[\hat{J}_{\mathrm{PDIS}}^{T-1-(t+1)}]\right]
PDISのバリアンスと比較すると第2項が異なっています.DRでは$w_t$の係数に$(\hat{Q}(s_t, a_t)-Q(s_t, a_t))$が組み込まれており $\hat{Q}$の精度が良いほどバリアンスを減少させます. これがDRの優れている部分であり,ベースラインである$Q$を組み込んだ利点です.具体的には$\hat{Q}(\cdot)$が$0<\hat{Q}(\cdot)<2Q(\cdot)$を満たせばDRはPDISよりもバリアンスの小さい推定量になります.
PDIS vs DR
軌跡の長さ$T$を変化させた場合のPDISとDRの比較を調べた結果を示しています.
PDISに比べDRでは$\hat{Q}$を入れたことで,バリアンスが少し小さくなっていることが実験でもわかります.PDISからDRへのバリアンスの減少幅は$\hat{Q}$に依存し,今回の実験例では大幅な改善はできていませんが$\hat{Q}$の推定精度が大きく外れすぎなければ,基本的にDRはPDISより優れた推定量となります.
Self-Normalized推定量
Self-Normalized推定量 [3-4]はバリアンスを減らすために,再三問題になっていた重要度重みのスケールを小さくしようとするモチベーションから生まれています.重要度重み$w_{\ast}$を以下に置き換えたものを利用します.
\tilde{w}_{\ast} := \frac{w_{\ast}}{\sum_{i=1}^n w_{\ast}}
ここで$\tilde{w}_{\ast} $は self-normalized重要度重み と呼ばれます.具体的にTISとPDISは以下のようにそれぞれSelf-Normalized TIS推定量(SNTIS)とSelf-Normalized PDIS推定量(SNPDIS)として定義できます.
\begin{align*}
\hat{J}_{\mathrm{SNTIS}} (\pi; \mathcal{D}) := \sum_{i=1}^n \sum_{t=0}^{T-1} \gamma^t \frac{w_{0:T-1}^{(i)}}{\sum_{i'=1}^n w_{0:T-1}^{(i')}} r_t^{(i)}
\end{align*}
\begin{align*}
\hat{J}_{\mathrm{SNPDIS}} (\pi; \mathcal{D}) := \sum_{i=1}^n \sum_{t=0}^{T-1} \gamma^t \frac{w_{0:t}^{(i)}}{\sum_{i'=1}^n w_{0:t}^{(i')}} r_t^{(i)}
\end{align*}
Self-Normalized推定量は今まで重要度重みを利用するすべての推定量で利用でき,バリアンスを抑える手段として非常に有効です.
TIS vs SNTIS
ここではTISと,TISをSelf-NormalizedしたSNTISを比較します.
バイアスはTISと同程度に保ちつつ,バリアンスを大幅に減らすことに成功しています.結果としてMSEも改善されています.
ここまで TIS → PDIS → DR → Self-Normalized と見てきましたが,どの推定量もバリアンスの発生原因になっていた重要度重みをどのように変形するかを考えていました.ただしこれらは重要度重みが軌跡の長さに依存してしまっているため,軌跡の長さが長くなった場合の根本的な解決にはなっていません.
Marginalized Importance Sampling推定量
ここまでの推定量では,軌跡の長さが長い場合に対応できませんでした.これに対して重要度重み自体を変え,新しい重要度重みを利用したMarginalized Importance Sampling推定量[3-5][3-6]が提案されています.
\begin{align*}
\rho(s_t, a_t) &:= \frac{d_t^{\pi}(s_t, a_t) }{ d_t^{\pi_0}(s_t, a_t) }\\
\rho(s_t) &:= \frac{d_{t}^{\pi}(s_t)\pi(a_t|s_t)}{ d_t^{\pi_0}(s_t)\pi_0(a_t|s_t)}
\end{align*}
$\rho(s_t, a_t)$を 状態行動周辺化重要度重み , $\rho(s_t)$を 状態周辺化重要度重み と呼びます.$d_t^{\pi}(s_t, a_t)$は方策$\pi$での$s_t, a_t$の観測確率, $d_t^{\pi}(s_t)$は方策$\pi$での$s_t$の観測確率を表します.この周辺化重要度重みを利用することで,今までのバリアンスによる問題を根本的に解決しバリアンスを大幅に抑えることが可能になります.上のように重要度重みを定めた時,State-Action Marginal Importance Sampling推定量(SAMIS)とState Marginal Importance Sampling推定量(SMIS)は以下のように定義されます.
\large{
\hat{J}_{\mathrm{SAMIS}} (\pi; \mathcal{D})
:= \frac{1}{n} \sum_{i=1}^n \sum_{t=0}^{T-1} \gamma^t \rho(s_t^{(i)}, a_t^{(i)}) r_t^{(i)}}
\large{
\hat{J}_{\mathrm{SMIS}} (\pi; \mathcal{D})
:= \frac{1}{n} \sum_{i=1}^n \sum_{t=0}^{T-1} \gamma^t \rho(s_t^{(i)}) w_t(s_t^{(i)}, a_t^{(i)}) r_t^{(i)}
}
重要度重みの定義を変えていますが,PDISと同様に共通サポートの仮定のもとでSAMISとSMISは不偏性を満たします.
\mathbb{E}_{\tau}[\hat{J}_{\mathrm{SAMIS}} (\pi; \mathcal{D})]= J(\pi)
証明
$d^{\pi}(s, a) := \left(\sum_{t=0}^{T-1} \gamma^{t} d_t^\pi(s, a)\right) /\left(\sum_{t=0}^{T-1}\gamma^{t}\right)$を利用します
\begin{align*}
\mathbb{E}_{\tau}[\hat{J}_{\mathrm{SAMIS}} (\pi; \mathcal{D})]
&= \mathbb{E}_{\tau \sim p_{\pi_0}}\left[\sum_{t=0}^{T-1}\frac{d_t^{\pi}(s_t, a_t)}
{d_t^{\pi_0}(s_t, a_t)} \gamma^{t}r_t \right]\\
&= \sum_{s, a}\sum_{t=0}^{T-1}d_t^{\pi_0}(s_t, a_t)\frac{d^{\pi}(s, a)}
{d^{\pi_0}(s, a)} \gamma^{t}R(s, a) \\
&=\left( \sum_{t=0}^{T-1}\gamma^{t}\right)\sum_{s, a}d^{\pi_0}(s, a)\frac{d^{\pi}(s, a)}
{d^{\pi_0}(s, a)} R(s, a) \\
&=\left( \sum_{t=0}^{T-1}\gamma^{t}\right)\sum_{s, a}d^{\pi}(s, a) R(s, a) \\
&= \sum_{s, a}\sum_{t=0}^{T-1}d_t^{\pi}(s_t, a_t)\gamma^{t}R(s, a) \\
&= \mathbb{E}_{\tau \sim p_{\pi}}\left[\sum_{t=0}^{T-1} \gamma^{t}r_t\right]\\
&=J(\pi)
\end{align*}
\mathbb{E}_{\tau}[\hat{J}_{\mathrm{SMIS}} (\pi; \mathcal{D})]= J(\pi)
証明
$d^{\pi}(s) := \left(\sum_{t=0}^{T-1} \gamma^{t} d_t^\pi(s)\right) /\left(\sum_{t=0}^{T-1} \gamma^{t}\right)$を利用します
\begin{align*}
\mathbb{E}_{\tau}[\hat{J}_{\mathrm{SMIS}} (\pi; \mathcal{D})]
&= \mathbb{E}_{\tau \sim p_{\pi_0}}\left[\sum_{t=0}^{T-1}\frac{d_t^{\pi}(s_t)\pi(a_t | s_t)}
{d_t^{\pi_0}(s_t)\pi_0(a_t | s_t)} \gamma^{t}r_t \right]\\
&= \sum_{s, a}\sum_{t=0}^{T-1}d_t^{\pi_0}(s_t, a_t)\pi_0(a_t | s_t)\frac{d^{\pi}(s)\pi(a_t | s_t)}
{d^{\pi_0}(s)\pi_0(a_t | s_t)} \gamma^{t}R(s, a) \\
&= \sum_{s, a}\sum_{t=0}^{T-1}d_t^{\pi_0}(s_t, a_t)\pi(a_t | s_t)\frac{d^{\pi}(s)}
{d^{\pi_0}(s)} \gamma^{t}R(s, a) \\
&=\left( \sum_{t=0}^{T-1}\gamma^{t}\right)\sum_{s, a}d^{\pi_0}(s)\frac{d^{\pi}(s)}
{d^{\pi_0}(s)} \pi(a | s)R(s, a) \\
&=\left( \sum_{t=0}^{T-1}\gamma^{t}\right)\sum_{s, a}d^{\pi}(s) \pi(a | s)R(s, a) \\
&= \sum_{s, a}\sum_{t=0}^{T-1}d_t^{\pi}(s_t)\pi(a_t|s_t)\gamma^{t}R(s, a) \\
&= \mathbb{E}_{\tau \sim p_{\pi}}\left[\sum_{t=0}^{T-1} \gamma^{t}r_t\right]\\
&=J(\pi)
\end{align*}
Marginal推定量は周辺化重要度重み$\rho(s,a), \rho(s)$が既知の場合,不偏推定量となりますが,真の周辺化重要度重みは多くの場合利用できません.したがって周辺化重要度重みを推定し,推定した重みを利用することになります.この場合周辺化重要度重みの推定誤差によるバイアスが発生します.
PDIS vs SAMIS
ここでは軌跡の長さ$T$を変化させた場合で,State-Action Marginal推定量のSAMISとPDISを比較していきます.
SAMISは状態行動周辺化重要度重みの推定によるバイアスが発生していますが,ここまで重要度重みを利用するどの推定量でも問題になっていた軌跡の長さが長い場合のバリアンスを大幅に減らすことができています.そのためSAMISは重要度重みを使いつつバリアンスを抑える推定量になっています.
PDISとSAMISはバイアス・バリアンスに関してトレードオフの関係にあり,最後にこれら二つの推定量を組み合わせた発展的な推定量を紹介します.
Spectrum of Off-Policy 推定量(SOPE)
周辺化重要度重みは,意思決定単位での重要度重みによるバリアンスを抑えた一方で,周辺化重要度重みの推定誤差によってバイアスが発生する可能性を紹介しました.これに対してバイアスとバリアンスのトレードオフをより柔軟に制御するために,意思決定単位での重要度重みと周辺化重要度重みの間をとった重要度重みを使用したSpectrum of Off-Policy 推定量(SOPE) [3-8]が提案されました.
状態行動周辺化重みを利用した場合の重要度重み
\begin{align*}
w_{\mathrm{SOPE}}(s_t, a_t) &=
\begin{cases}
\prod_{t'=0}^{k-1} w_t(s_{t'}, a_{t'}) & \mathrm{if} \, t < k \\
\rho(s_{t-k}, a_{t-k}) \prod_{t'=t-k+1}^{t} w_t(s_{t'}, a_{t'}) & \mathrm{otherwise}
\end{cases} \\
\end{align*}
状態周辺化重みを利用した場合の重要度重み
\begin{align*}
w_{\mathrm{SOPE}}(s_t, a_t) &=
\begin{cases}
\prod_{t'=0}^{k-1} w_t(s_{t'}, a_{t'}) & \mathrm{if} \, t < k \\
\rho(s_{t-k}) \prod_{t'=t-k}^{t} w_t(s_{t'}, a_{t'}) & \mathrm{otherwise}
\end{cases}
\end{align*}
具体的にSAMISとPDISを組み合わせたSOPE-SAMISは下のように定義できます.
\begin{align*}
&\hat{J}_{\mathrm{SOPE-SAMIS}} (\pi; \mathcal{D})\\
&:= \frac{1}{n} \sum_{i=1}^n \sum_{t=0}^{k-1} \gamma^t w_{\mathrm{SOPE}}^{(i)}(s_t, a_t) r_t^{(i)}\\
&=\frac{1}{n} \sum_{i=1}^n \sum_{t=0}^{k-1} \gamma^t w_{0:t}^{(i)} r_t^{(i)}
+ \frac{1}{n} \sum_{i=1}^n \sum_{t=k}^{T-1} \gamma^t \rho(s_{t-k}^{(i)}, a_{t-k}^{(i)}) w_{t-k+1:t}^{(i)} r_t^{(i)}
\end{align*}
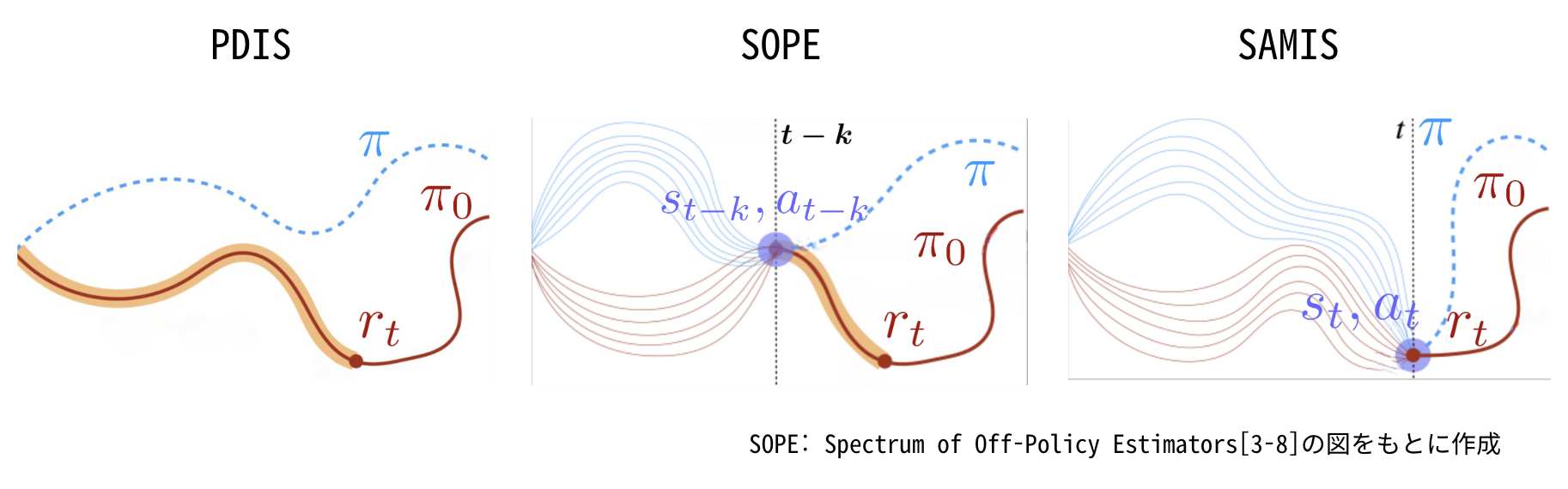
上の図はPDIS,SOPE,SAMISのイメージです.PDISは意思決定単位での重要度重み$w_{0:t}$によって$t$期までの軌跡を考慮し,$r_t$は重みづけされています(オレンジ色の部分).一方SAMISは周辺化重要度重み$\rho$によって$(s_t, a_t)$に出現する確率を考慮し,$r_t$を重みづけしています(紫の部分).SOPEは意思決定単位での重要度重みと周辺化重要度重みを組み合わせ,確率分布と軌跡のずれの両方を考慮しています.$t<k$の場合はPDISと同じ意思決定単位での重要度重みを利用し,$t \geq k$の場合はSAMISと同じ周辺化重要度重みを利用しています.つまりPDISとSAMISを組み合わせた推定量としてSOPEは提案されています.
PDIS vs SAMIS vs SOPE
簡易実験ではSOPEをSAMISとPDISに対して比較しています.横軸は$k$でSOPEがどこまでPDISと同じ重要度重みを使うかを表しているためnumber of step pdisとしています.$k$を変えることでMarginal推定量とPDIS推定量のバランスをコントロールできます.
図から分かるようにSOPEは$k=0$のときSAMISと一致し,$k=T$(軌跡の長さ)のときPDISと一致します.$k$を大きくするとバイアスを抑えられ,$k$を小さくするとバリアンスを抑えることができます.SOPEは$k$を調節することでバイアスとバリアンスのトレードオフを考慮し,SAMIS・PDISよりMSEが小さくなるように設計することが可能です.
まとめ
本記事では強化学習において,新たな方策の価値を過去の方策から集められたデータのみを利用して評価するオフ方策評価を見てきました.特にバイアスとバリアンスの観点からオフ方策評価の推定量をいくつか紹介しました.バイアスに弱いDM,バリアンスに弱いTISからバリアンスを抑えられるようにPDIS,DR,SelfNormalized,MISを紹介し,PDISとMISを組み合わせたSOPEについて紹介しました.手法の複雑さと性能はトレードオフにあり,実務で利用する際は一つ一つの推定量の性質を正しく理解し,選択することが重要になります.
関連研究と今後の展望
この章ではオフ方策評価に関連して自分の関心がある部分や勉強しているトピックにについて独自の観点でまとめています.文脈付きバンディットとランキングとの関連,リスクを考慮したオフ方策評価,オフ方策評価の効果的な利用の3つの観点で紹介します.
文脈付きバンディットとランキングとの関連
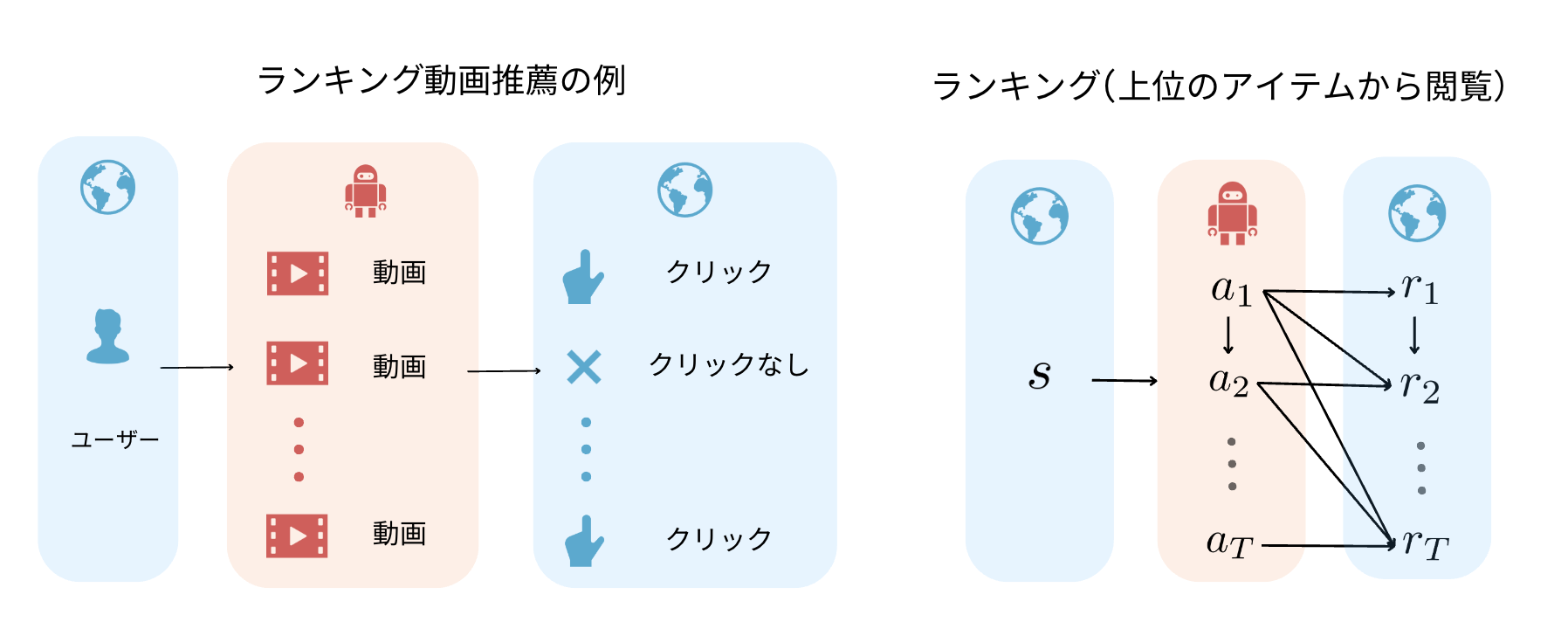
強化学習のオフ方策評価以外にも,文脈付きバンディット(contextual bandit) の設定におけるオフ方策評価推定量[5-1]が同じように定義されています.文脈付きバンディットと強化学習の違いは状態が推移するかどうかにあります.強化学習では状態$s$が時刻$t$によって変わる問題設定を考えていますが,文脈付きバンディットでは状態に当たる部分が文脈となりユーザーなどで固定されており,強化学習の特殊ケース(時系列依存性のないより簡易なケース)になっています.
興味深い文脈付きバンディットの特殊設定として,単一のアイテムではなく,複数のアイテムを選択するランキングの設定が存在します.ランキングでは上の動画推薦の例のようにユーザーに対してアイテムを順番に推薦します.するとユーザーのクリック有無などが報酬として,各動画ごとに発生します.このランキングにおいてユーザーが得る報酬$r$は上位のアイテムのみから影響を受ける(上位のアイテムから閲覧していく)ことを仮定すると,過去の状態のみから影響を受ける強化学習と似た問題設定となります.この性質を利用して本記事で紹介した強化学習でのDRをランキングにおいて応用した手法が提案されています.[5-2] このようにオフ方策評価は強化学習だけでなく,文脈付きバンディット・ランキングの設定においても議論されており,様々な設定を相互的に学習することでオフ方策評価に対して理解を深めることができます.
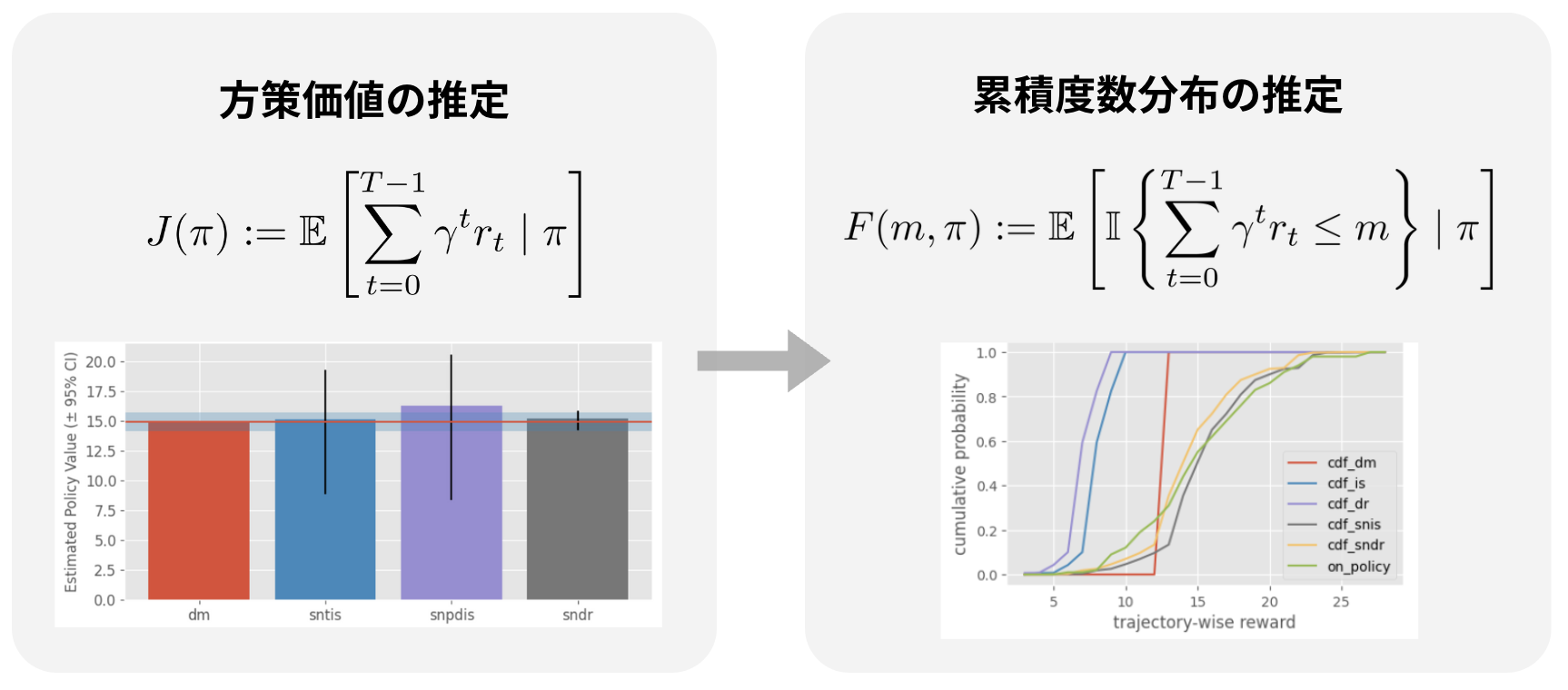
リスクを考慮したオフ方策評価
本記事ではオフ方策評価について期待報酬を推定する推定量のみを紹介しましたが,実務で使われる医療や自動運転・金融投資などでは平均的な性能 (期待報酬) だけでなく,どれだけその方策がリスクを持つかも重要な観点になってきます.リスクを正確に把握するためには,報酬のバリアンスはどうなるのか,下位10%の確率でどのような性能になるのかなど,性能全体の分布を知る必要があります.これに対して,分布オフ方策評価[5-3] [5-4]の推定量が提案されており,報酬の累積度数分布を推定することでリスク(CVaR,バリアンスなどのリスク指標によって) を考慮できるようになります.不確実性が大きい強化学習ではよりリスクの観点が重要になり,今後オフ方策評価の実応用が増えていくにつれより発展していく分野になるはずです.
オフ方策評価の効果的な利用
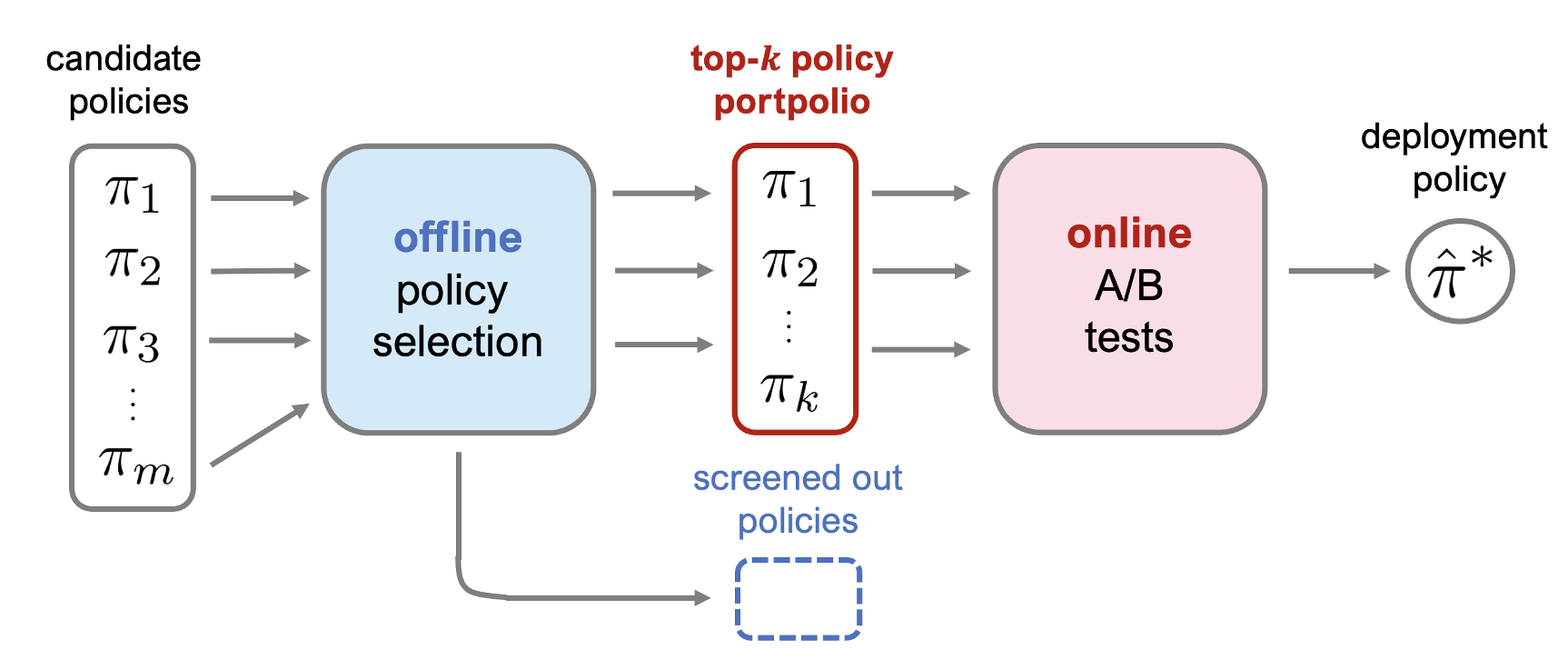
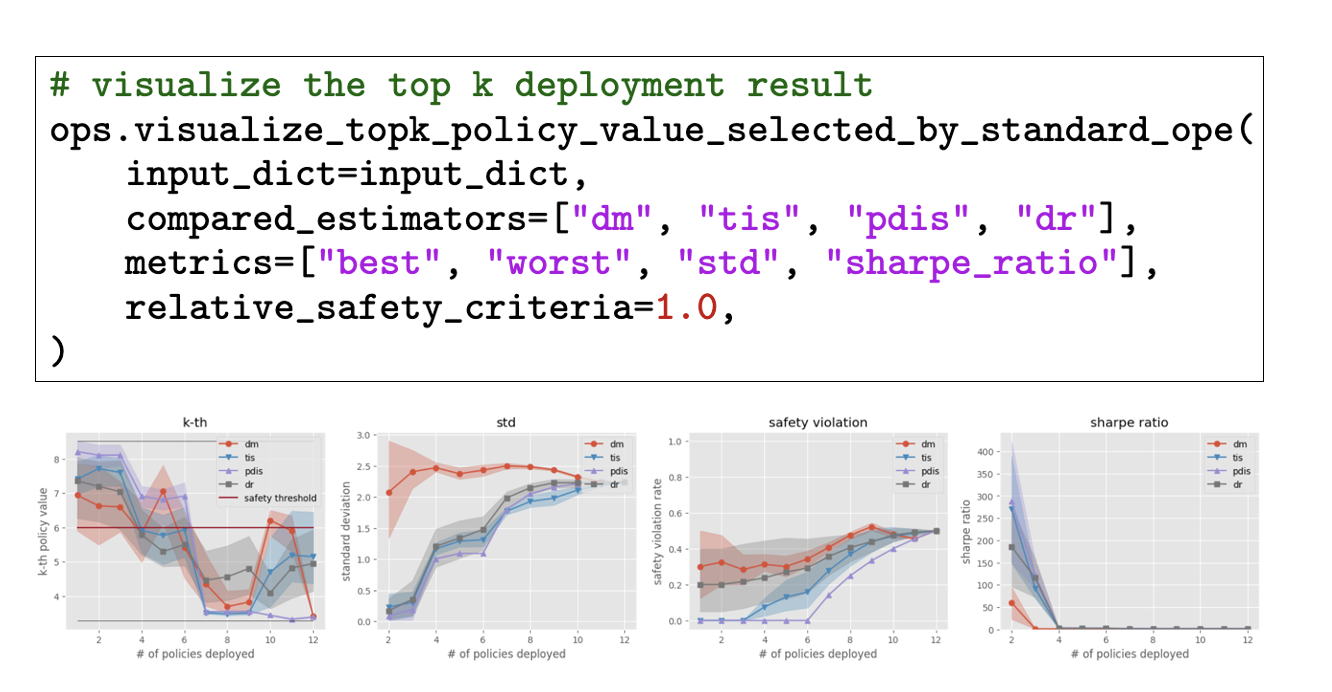
オフ方策評価において,過去の方策の分布が新たな方策の分布と大きく乖離している場合に分布シフトと呼ばれる問題が発生し,推定がうまくいかない状況が考えられます.方策の評価は不確実性が高いため,オフ方策評価によって評価した方策をそのまま実施するのではなく,実際の環境でオンライン実験をおこなった後に実施する方策を決定する流れを踏むことになります.[5-5] つまりオフ方策評価では実施する方策を決めるのではなく,オンライン実験に回す方策を決定する役割を持ちます.[5-6] このようにオフ方策評価が単体で行われるのではなく,全体の中の一部として機能する場合,どのような推定量が望ましいのか,推定量の性能をどう評価するのかが重要な課題になります.そもそも実施する方策を決定する際の理想的な流れを考える視点も面白そうです.オンライン強化学習・オフライン強化学習・オフ方策評価・オンライン評価とある中で,各々の性能を向上させるのはもちろんですが,全体の流れの中でどう機能させるか,また全体の流れをどう設計するかも議論の余地があるのではないかと思います.そのうちの一つとして,推定量の性能をどう評価するかに着目し,オフ方策評価の新たな性能検証指標を提案する研究を行いました.興味のある方はぜひ見てみてください.
論文[Towards Assessing and Benchmarking Risk-Return Tradeoff of Off-Policy Evaluation]
おわりに
強化学習やバンディットの分野は研究はされているものの,行動数が多い場合(動画や音楽の推薦では何万ものアイテムが存在),正確な推定の難しさからほとんど実務では利用されていないのが現状です.まだ多くの研究段階・未解決の問題も多く存在しますが,オフ方策評価を使うことができるようになれば様々な場面で応用されていくはずです.
自分自身も強化学習におけるオフ方策評価に関して,この章で紹介した領域の勉強をしつつ知見を増やせていけたらなと思っています.本記事を通して,このオフ方策評価の研究の魅力を少しでも感じていただけたら嬉しいです.長くなりましたが,最後まで読んでいただきありがとうございました.
appendix : SCOPE-RLの紹介
最後に今回の実装で利用したライブラリ「SCOPE-RL」を簡単に紹介します.「SCOPE-RL」は博報堂テクノロジーズ,半熟仮想,東工大中田研との共同研究において開発していたオフライン強化学習とオフ方策評価に関するオープンソースソフトウェアです.本記事で紹介したオフ方策評価だけでなく,データ収集・オフライン強化学習から,そのオフラインでの性能評価・モデル選択の実装を一貫して行えるライブラリです.
オフライン評価に関しては今回紹介した手法のほかに性能分布全体を評価する最先端の研究や,さらには数々のオフライン評価指標を多角的に性能検証するための機能までをも実装しています.documentationやquickstartノートブックも充実しているため,ぜひチェックしてみてください.
- SCOPE-RL documentation: https://scope-rl.readthedocs.io/en/latest/
- SCOPE-RL repository: https://github.com/hakuhodo-technologies/scope-rl
- pip: https://pypi.org/project/scope-rl/
- 博報堂テクノロジーズからのプレスリリース
https://prtimes.jp/main/html/rd/p/000000007.000113498.html - 東工大ニュース
https://www.titech.ac.jp/news/2024/069044
参考文献
全体的に
ゼロから始めてオフライン強化学習とConservative Q-Learningを理解する[link]
Off-Policy Evaluationの基礎とZOZOTOWN大規模公開実データおよびパッケージ紹介[link]
斎藤康毅.ゼロから作るDeep Learning ❹ 強化学習編. オライリー・ジャパン, 2022.
オフ方策評価の推定量
[DM][3-1]Alina Beygelzimer and John Langford. The offset tree for learning with partial labels. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 129–138. 2009.[link]
[TIS, PDIS][3-2]Doina Precup, Richard S. Sutton, and Satinder P. Singh. Eligibility traces for off-policy policy evaluation. In Proceedings of the 17th International Conference on Machine Learning, 759––766. 2000.[link]
[DR][3-3]Nan Jiang and Lihong Li. Doubly robust off-policy value evaluation for reinforcement learning. In Proceedings of the 33rd International Conference on Machine Learning, volume 48, 652–661. PMLR, 2016.[link]
[Self-Normalized][3-4]Nathan Kallus and Masatoshi Uehara. Intrinsically efficient, stable, and bounded off-policy evaluation for reinforcement learning. In Advances in Neural Information Processing Systems, 3325–3334. 2019.[link]
[MIS][3-5]Masatoshi Uehara, Jiawei Huang, and Nan Jiang. Minimax weight and q-function learning for off-policy evaluation. In Proceedings of the 37th International Conference on Machine Learning, 9659–9668. PMLR, 2020.[link]
[MIS][3-6]Qiang Liu, Lihong Li, Ziyang Tang, and Dengyong Zhou. Breaking the curse of horizon: infinite-horizon off-policy estimation. Advances in Neural Information Processing Systems, 2018.[link]
[DRL] [3-7]Nathan Kallus and Masatoshi Uehara. Double reinforcement learning for efficient off-policy evaluation in markov decision processes. Journal of Machine Learning Research, 2020.[link]
[SOPE][3-8]Christina Yuan, Yash Chandak, Stephen Giguere, Philip S Thomas, and Scott Niekum. Sope: spectrum of off-policy estimators. Advances in Neural Information Processing Systems, 34:18958–18969, 2021.[link]
関連研究と今後の展望
[5-1]Yuta Saito, Shunsuke Aihara, Megumi Matsutani, and Yusuke Narita. Open bandit dataset and pipeline: towards realistic and reproducible off-policy evaluation. Advances in Neural Information Processing Systems, 2021.[link]
[5-2]Haruka Kiyohara, Yuta Saito, Tatsuya Matsuhiro, Yusuke Narita, Nobuyuki Shimizu, and Yasuo Yamamoto. Doubly Robust Off-Policy Evaluation for Ranking Policies under the Cascade Behavior Model. In Proceedings of the 15th ACM International Conference on Web Search and Data Mining. 487–497, 2022.[link]
[5-3]Audrey Huang, Liu Leqi, Zachary Lipton, and Kamyar Azizzadenesheli. Off-policy risk assessment in contextual bandits. In Advances in Neural Information Processing Systems, volume 34, pages 23714–23726, 2021.[link]
[5-4]Audrey Huang, Liu Leqi, Zachary Lipton, and Kamyar Azizzadenesheli. Off-Policy Risk Assessment for Markov Decision Processes. In Proceedings of the 25th International Conference on Artificial Intelligence and Statistics (AISTATS), Vol. 151. PMLR, 5022-5050.[link]
[5-5]Vladislav Kurenkov and Sergey Kolesnikov. Showing your offline reinforcement learning work: Online evaluation budget matters. In Proceedings of the 39th International Conference on Machine Learning, pages 11729–11752. PMLR, 2022.[link]
[5-6]Haruka Kiyohara, Ren Kishimoto, Kosuke Kawakami, Ken Kobayashi, Kazuhide Nakata and Yuta Saito. Towards Assessing and Benchmarking Risk-Return Tradeoff of Off-Policy Evaluation, 2023.[link]

![result_fig_n_trajectories_['DM', 'TIS'].png](https://qiita-user-contents.imgix.net/https%3A%2F%2Fqiita-image-store.s3.ap-northeast-1.amazonaws.com%2F0%2F3535628%2F64b54420-cd3c-6e10-ec0b-144705b229d8.png?ixlib=rb-4.0.0&auto=format&gif-q=60&q=75&s=b18d6fb01a2850e4f8e23c7e612dbc2c)
![result_fig_step_per_trajectory_['DM', 'TIS'].png](https://qiita-user-contents.imgix.net/https%3A%2F%2Fqiita-image-store.s3.ap-northeast-1.amazonaws.com%2F0%2F3535628%2Fb7b12434-5814-0bdb-017a-14d33d7ec4e0.png?ixlib=rb-4.0.0&auto=format&gif-q=60&q=75&s=3146b9f3fe172ced2a3384d82001e3b1)
![result_fig_step_per_trajectory_['TIS', 'PDIS'].png](https://qiita-user-contents.imgix.net/https%3A%2F%2Fqiita-image-store.s3.ap-northeast-1.amazonaws.com%2F0%2F3535628%2F6f0ca639-a191-3b58-a9a6-3fa7a78c9284.png?ixlib=rb-4.0.0&auto=format&gif-q=60&q=75&s=ce580d006ed1f70fbfd61b4e6b35abd4)
![result_fig_step_per_trajectory_['PDIS', 'DR'].png](https://qiita-user-contents.imgix.net/https%3A%2F%2Fqiita-image-store.s3.ap-northeast-1.amazonaws.com%2F0%2F3535628%2Fd93b685a-9e37-86f8-a831-6661ffd6b876.png?ixlib=rb-4.0.0&auto=format&gif-q=60&q=75&s=2efceb159ece9b9a6784e771c54b6638)
![result_fig_step_per_trajectory_['TIS', 'SNTIS'].png](https://qiita-user-contents.imgix.net/https%3A%2F%2Fqiita-image-store.s3.ap-northeast-1.amazonaws.com%2F0%2F3535628%2F721e3069-ab97-b18a-5f5c-afb4a5571b36.png?ixlib=rb-4.0.0&auto=format&gif-q=60&q=75&s=13025d3c6b77d729780340c2366593db)
![result_fig_step_per_trajectory_['PDIS', 'SAMIS'].png](https://qiita-user-contents.imgix.net/https%3A%2F%2Fqiita-image-store.s3.ap-northeast-1.amazonaws.com%2F0%2F3535628%2F33ead3a6-0ca9-5afa-2f1f-077d62781a74.png?ixlib=rb-4.0.0&auto=format&gif-q=60&q=75&s=5054e49f34215d93dda1ebe51773358b)
![result_fig_n_step_pdis_['SAMIS', 'PDIS', 'SOPE'].png](https://qiita-user-contents.imgix.net/https%3A%2F%2Fqiita-image-store.s3.ap-northeast-1.amazonaws.com%2F0%2F3535628%2Fe6b6d422-dfde-68a8-7e61-271dde0e3c50.png?ixlib=rb-4.0.0&auto=format&gif-q=60&q=75&s=dd83e699d4255170660c2a1e4d84cfff)