はじめに
この記事はUnity #3 Advent Calendar 2020の9日目の記事です。
この記事では高速フーリエ変換(FFT)を使った海洋シミュレーション、FFT Oceanについて書いていこうと思います。Unityに限らずいろんなゲームエンジンで再現できるよう理論サイドも俯瞰しつつ、私が実装を通して理解したことをまとめています。
次に発展として、法線ベクトルの算出や、より波を尖らせてそれっぽくすることをやっていこうと思います。
最終的にはこんな絵ができあがります。

FFT Oceanについて
音声信号などの波形はフーリエ変換することで周波数を得ることができます。逆に周波数情報から波形を求めることができます→逆フーリエ変換。
FFT Oceanは海面の高さを周波数から逆フーリエ変換で求めてしまおうというものです。すなわち周波数スペクトルが大事になってきます。
この周波数スペクトルをTessendorfの書いた手法で生成します。
https://evasion.imag.fr/Membres/Fabrice.Neyret/images/fluids-nuages/waves/Jonathan/articlesCG/simulating-ocean-water-01.pdf
一部のゲームや映画(タイタニック)などいろんなところに使われている有名な(?)手法のようです。
CUDA Sampleの中にもあったりします。
https://docs.nvidia.com/cuda/cuda-samples/index.html#cuda-fft-ocean-simulation

実装
0.概要をざっくりと
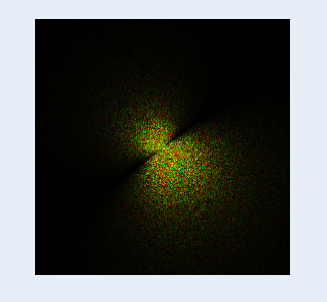
1、まずは事前計算で左の画像をCPUで計算しGPU上のメモリに載せておく
2、それをベースに毎フレーム真ん中の画像をGPU上で生成(tはtime)。これが周波数に相当
3、GPU上で逆フーリエ変換をして右の画像(=海面の高さ)を生成
4、右の画像から実際の位置にレンダリング
※数式上、最初から最後まで複素数がでてきますが、画像でいうと左の画像と中央の画像ではr,gが実数,虚数に対応、右の画像は実数を白で表現しています。CUDA Sampleでも海面の高さには実数のみを使っていました。
1.事前計算でh0(k)をCPUで計算しGPU上のメモリに載せておく
\tilde{h}_0(\vec{k}) =\frac{1}{\sqrt{2}}(\xi_r+i\xi_i)\sqrt{P_h(\vec{k})}
です。
正直最初ほとんどの記号が意味ワカンナイ状態でしたが、他人のコードを見ながらちょっとずつ理解していった感じです。ひとつずつ見ていきましょう。
Kの定義
\vec{k}=(k_x,k_z)=(\frac{2\pi n}{L_x},\frac{2\pi m}{L_z})
-\frac{N}{2}\leq n<\frac{N}{2}\\
-\frac{M}{2}\leq m<\frac{M}{2}\\
n,mは整数
早速難しそうですが、kはN×Mの二次元配列みたいなもんです。画像の各ピクセルにkの各要素が対応している感じです。
今後FFTで実装することを考慮し2のべき乗とし、今は$N=256$,$M=256$くらいで考えておけばよいです。
また$L_x,L_z$は海面サイズです。
こちらに関しては、スケールの問題なので何でもいいと最初思ってましたが論文にはこうありました。
・$dx=L_x/N > 2$
・$dz=L_z/M > 2$
・$dx,dz=2.5$ が最も良い (←自信ないのですが間違ってたらコメントしてください)
正規分布に基づく乱数
$\xi_r$と$\xi_i$はランダムな数です。具体的には正規分布する乱数が必要です。なんでこう難しそうな記号を使うのか・・・
コードではボックス=ミュラー法を使っています。これは標準正規分布する乱数を生成する手法です。
参考
JavaScriptでBox-Muller法による正規分布からのサンプリング
// Generates Gaussian random number with mean 0 and standard deviation 1.
Vector2 Gauss()
{
var u1 = Random.value;
var u2 = Random.value;
var logU1 = -2f * Mathf.Log(u1);
var sqrt = (logU1 <= 0f) ? 0f : Mathf.Sqrt(logU1);
var theta = Mathf.PI * 2.0f * u2;
var z0 = sqrt * Mathf.Cos(theta);
var z1 = sqrt * Mathf.Sin(theta);
return new Vector2(z0, z1);
}
Phillips Spectrum
最後に残った$P_h(\vec{k})$の中身はこれです。
P_h(\vec{k})=A\frac{e^\frac{-1}{(kL)^2}}{k^4}|\vec{k}\cdot\vec{\omega}|^2
えー、これも一つずつ見ていきましょう。
$A$:これは定数です。最終的な波の高さのスケールだと思ってください。
$e$:これはさすがに自然対数の底でいいでしょう。
$k$:$\vec{k}$ の長さ。sqrt(k.xk.x+k.yk.y)とかで求められますね。
$L$:$L=V^2/g$ ここで$V$は風速 つまり定数、$g$は重力定数で$g=9.81$です。
$\vec{\omega}$:風向きの単位ベクトル(風がないと波が起きません)
これですべてそろいました。
なお、この式の意味するところですが理論的に導き出されたというよりは、テッセンドルフさんが必死に海を観察し導き出された"経験的"な式らしいです。なのであまり細かいことを気にせずに、こういうものだと思ったほうがいいです、精神衛生上。
で、ここまではまぁいいのですが、論文にはさらにこうあります。

多分ですが|k|が大きいとなにかがダメなようで、ちょっと修正しろと言ってるんですね。
他のコードも参考に下記のような修正を加えるようにしました。
P_{h_{modify}}(\vec{k})=P_h(\vec{k})×e^{-k^2(0.001L)^2}
using UnityEngine;
public class Phillips : MonoBehaviour
{
public const uint meshSize = 256;
public const uint seasizeLx = meshSize * 5 / 2;
public const uint seasizeLz = meshSize * 5 / 2;
const float G = 9.81f; // gravitational constant
const float A = 0.000001f; // wave scale factor A - constant
const float windSpeed = 30.0f;
const float windDir = Mathf.PI * 1.234f; //wind angle in radians
// Generates Gaussian random number with mean 0 and standard deviation 1.
Vector2 Gauss()
{
var u1 = Random.value;
var u2 = Random.value;
var logU1 = -2f * Mathf.Log(u1);
var sqrt = (logU1 <= 0f) ? 0f : Mathf.Sqrt(logU1);
var theta = Mathf.PI * 2.0f * u2;
var z0 = sqrt * Mathf.Cos(theta);
var z1 = sqrt * Mathf.Sin(theta);
return new Vector2(z0, z1);
}
// Phillips spectrum
// (Kx, Ky) - normalized wave vector
float Generate_Phillips(float Kx, float Ky)
{
float k2mag = Kx * Kx + Ky * Ky;
if (k2mag == 0.0f)
{
return 0.0f;
}
float k4mag = k2mag * k2mag;
// largest possible wave from constant wind of velocity v
float L = windSpeed * windSpeed / G;
float k_x = Kx / Mathf.Sqrt(k2mag);
float k_y = Ky / Mathf.Sqrt(k2mag);
float w_dot_k = k_x * Mathf.Cos(windDir) + k_y * Mathf.Sin(windDir);
float phillips = A * Mathf.Exp(-1.0f / (k2mag * L * L)) / k4mag * w_dot_k * w_dot_k;
// damp out waves with very small length w << l
float l2 = (L / 1000) * (L / 1000);
phillips *= Mathf.Exp(-k2mag * l2);
return phillips;
}
// Generate base heightfield in frequency space
public Vector2[] Generate_h0()
{
Vector2[] h0 = new Vector2[meshSize * meshSize];
for (uint y = 0; y < meshSize; y++)
{
for (uint x = 0; x < meshSize; x++)
{
float kx = (-(int)meshSize / 2.0f + x) * (2.0f * Mathf.PI / seasizeLx);
float ky = (-(int)meshSize / 2.0f + y) * (2.0f * Mathf.PI / seasizeLz);
float P = Generate_Phillips(kx, ky);
if (kx == 0.0f && ky == 0.0f)
{
P = 0.0f;
}
uint i = y * meshSize + x;
h0[i] = Gauss() * Mathf.Sqrt(P * 0.5f);
}
}
return h0;
}
}
これでCPU上で$h_0(\vec{k})$を計算することができました。
後のコードに含まれていますが、GPUに転送するコードの一部を載せておきます。
Vector2[] h_h0;
ComputeBuffer d_h0;
void Start()
{
h_h0 = phillips.Generate_h0();//CPU側メモリ確保。サイズはsizeof(Vector2)*256*256
d_h0 = new ComputeBuffer(h_h0.Length, sizeof(float) * 2);//GPU側メモリ確保 サイズはsizeof(Vector2)*256*256
d_h0.SetData(h_h0);
}
余談 w_dot_kの6乗のとき
余談ですが、Phillips Spectrumの計算でw_dot_kを2乗ではなく6乗でやる流派もあるようです。6乗にすることで、風の方向に応じた波が今まで以上に際立つそうです。
余談 Donelan-Bannerというワード
これも余談ですがPhillips Spectrumを求めた後、Donelan-Banner方向拡張?(中国語の翻訳なのでわかりませんが)という謎の計算をしてかけているコードも見かけたので一応書いておきます。
https://zhuanlan.zhihu.com/p/96811613
2.それをベースに毎フレームh(k,t)をGPU上で生成(tはtime)
\tilde{h}(\vec{k},t)=\tilde{h}_0(\vec{k})e^{i\omega(k)t}+\tilde{h}_0^*(-\vec{k})e^{-i\omega(k)t}
ここで$ \tilde{h}_0^*$は$ \tilde{h}_0$の共役複素数です。※虚部を−1倍した複素数のことを共役複素数と言います。
あとhの上に乗ってる波線はチルダと読みますが特に深い意味はないので無視してください(なんか"似てる"的な意味合いがあるようです)
$\omega(k)=\sqrt{gk}$
$g$は重力定数 $=9.81$
$k$は$\vec{k}$の長さです。
$t$はtimeです。毎フレーム動的にh(k,t)が変わるということが分かります。
あと$e$の肩に虚数$i$が乗っています。高校数学でここまで習わないかもしれませんが、この計算は有名なヤツです。
オイラーの公式
$$ e^{i\theta} = \cos\theta + i\sin\theta $$
プログラム実装的にはどうすればよいかと言うと
「実数xが与えられるので$e^{ix}$を求めてください、cosとsin関数を駆使してね」
ということなので四則演算とsin,cosが書ければ実装できることがわかります。
したがってこんなコードになります。
GPU上にあるデータに対しての計算なのでCompute Shaderのコードになります。
#pragma kernel GenerateSpectrumKernel
#define PI 3.14159265358979323846264338328
RWStructuredBuffer<float2> h0;
RWStructuredBuffer<float2> ht;
int N;
int seasizeLx;
int seasizeLz;
float t;
float2 conjugate(float2 arg)
{
float2 f2;
f2.x = arg.x;
f2.y = -arg.y;
return (float2)f2;
}
float2 complex_exp(float arg)
{
return (float2)(cos(arg), sin(arg));
}
float2 complex_add(float2 a, float2 b)
{
return (float2)(a.x + b.x, a.y + b.y);
}
float2 complex_mult(float2 ab, float2 cd)
{
return (float2)(ab.x * cd.x - ab.y * cd.y, ab.x * cd.y + ab.y * cd.x);
}
[numthreads(256, 1, 1)]
void GenerateSpectrumKernel(uint2 id : SV_DispatchThreadID)
{
uint x = id.x;
uint y = id.y;
uint in_index = y * N + x;
uint in_mindex = (N - y) % N * N + (N - x) % N; // mirrored
uint out_index = y * N + x;
// calculate wave vector
float2 k;
k.x = (-(int)N / 2.0f + x) * (2.0f * PI / seasizeLx);
k.y = (-(int)N / 2.0f + y) * (2.0f * PI / seasizeLz);
// calculate dispersion w(k)
float k_len = sqrt(k.x * k.x + k.y * k.y);
float w = sqrt(9.81f * k_len);
if ((x < (uint)N) && (y < (uint)N))
{
float2 h0_k = h0[in_index];
float2 h0_mk = h0[in_mindex];
// output frequency-space complex values
ht[out_index] = complex_add(complex_mult(h0_k, complex_exp(w * t)), complex_mult(conjugate(h0_mk), complex_exp(-w * t)));
}
}
難しい点としては$ \tilde{h}_0(-\vec{k}) $のメモリアクセスかなと思います。
コードでいうとin_mindexの計算についてです。
in_mindexの計算
脇道にそれますがちょっと考えてみましょう(自分のメモ代わりにもなるので)
ここで h0[y*N+x] というように配列変数にアクセスし$\tilde{h}_0(\vec{k})$の値を取り出せたとします。
そのときx,yを使って$\tilde{h}_0(-\vec{k})$を取り出すにはどうしたらいいでしょう、という問題になります。
\vec{k}=(k_x,k_z)=(\frac{2\pi n}{L_x},\frac{2\pi m}{L_z})\\
n=-\frac{N}{2}+x\\
m=-\frac{M}{2}+y\\
0\leqq x<N\\
0\leqq y<M\\
x,yは整数
なのでマイナスは
-\vec{k}=(-k_x,-k_z)=(-\frac{2\pi n}{L_x},-\frac{2\pi m}{L_z})\\
ここから
-\vec{k}=(\frac{2\pi n'}{L_x},\frac{2\pi m'}{L_z})\\
とし\\
n'=-n=\frac{N}{2}-x=-\frac{N}{2}+(N-x)\\
m'=-m=\frac{M}{2}-y=-\frac{M}{2}+(M-y)\\
つまり
x'=N-x\\
y'=M-y\\
としてx' y'を使ってh0[y'*N+x'] というようアクセスすることで$ \tilde{h}_0(-\vec{k}) $が得られることがわかりました。
ただしx=0 や y=0のときx'=N y'=Mとなり範囲外のアクセスになるのでx'=Nのときはx'=0(y'のときも同様)の値を使って計算してしまっています。ここは目を瞑ります。
Dispatchグループ数について
このCompute Shaderコードでは
id.x id.yが0~255になることを想定しているので、C#のDispatch側でも
shader.Dispatch(kernel_GenerateSpectrumKernel, 1, 256, 1);
このようにグループ数を指定する必要があります。
3.GPU上で逆フーリエ変換をして右の画像(=海面の高さ)を生成
さきほど求めた画像$\tilde{h}(\vec{k},t)$をもとに逆2DFFTをかけ海面の高さを算出します。
式で書くと
h(\vec{x},t)=\sum_{k}\tilde{h}(\vec{k},t)e^{i\vec{k}\cdot\vec{x}}\\
を求めたいです。
その計算の仕方ですが、ちょっと長めの説明をしたいので先に結論だけ言います。

まずこの画像を普通に2次元逆FFTで変換します。そのあと
・計算結果全体を(N/2,M/2)ずらす
・要素のindex x,zが(x+z)%2==1となる要素に-1をかける
をすればよいです。
2次元FFT
まずは普通の方法からおさらいしましょう。
2DFFTのやりかたはまず横方向にそれぞれFFTを実行し
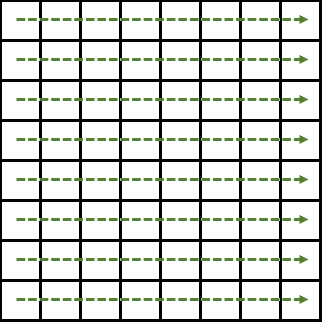
その結果を今度は縦方向にFFTします。
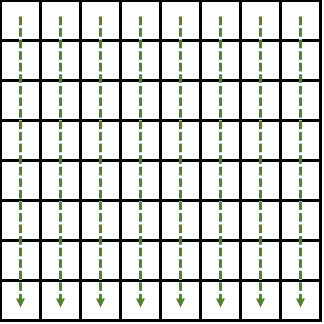
iFFT(逆フーリエ変換)でも同様です。また縦→横の順にやっても答えは変わりません。
FFTの具体的な計算方法などは下記参照を。
Compute Shaderで2DFFTしているコード
下町のナポレオン Compute ShaderでFFTと畳み込み演算でブラー
Compute Shaderではないが、ループ型のFFT計算のコードが乗ってる記事
任意要素数の高速フーリエ変換
高速フーリエ変換FFTを理解する
FFT(Fast Fourier transform)をC++で実装する
DFTから理解する
離散フーリエ変換(DFT)の仕組みを完全に理解する
マイナス周波数成分から始まるスペクトルのiFFT
先ほどの式を再掲します。
h(\vec{x},t)=\sum_{k}\tilde{h}(\vec{k},t)e^{i\vec{k}\cdot\vec{x}}\\
ここで$\vec{k}$と$\vec{x}$の定義は
\vec{k}=(k_x,k_z)=(\frac{2\pi n}{L_x},\frac{2\pi m}{L_z})\\
-\frac{N}{2}\leq n<\frac{N}{2}\\
-\frac{M}{2}\leq m<\frac{M}{2}\\
n,mは整数
\vec{x}=(x,z)=(\frac{qL_x}{N},\frac{rL_z}{M})\\
-\frac{N}{2}\leq q<\frac{N}{2}\\
-\frac{M}{2}\leq r<\frac{M}{2}\\
q,rは整数
こうなっています。
ベクトルを成分別に分けて書くと上記の式はこうなります。
h(\vec{x},t)=h(x,z,t)=\sum_{m=-\frac{M}{2}}^{\frac{M}{2}-1}\sum_{n=-\frac{N}{2}}^{\frac{N}{2}-1}\tilde{h}(\frac{2\pi n}{Lx},\frac{2\pi m}{Lz},t)e^{i(\frac{2\pi n}{Lx}x+\frac{2\pi m}{Lz}z)}
n,m,x,zがマイナスから始まっていることに注意です。なので普通にFFT(iFFT)の計算を適応しただけだと間違った答えになります。
画像をみればわかるとおり、中心に周波数0成分がきていますね。

一応証明
普通にFFT(iFFT)の計算を適応しただけだと間違った答えになるので、さっき太文字で書いたやり方でやる必要があります。
本当にそれでいいのか証明させてください・・・
まずは0オリジンで考えたいのでこうします。
n'\in{(0,1,2,3,...,N-1)}\\
m'\in{(0,1,2,3,...,M-1)}\\
x'\in{(0,1,2,3,...,N-1)}\\
z'\in{(0,1,2,3,...,M-1)}\\
x''\equiv x'+N/2 \quad(mod \quad N)\\
z''\equiv z'+M/2 \quad(mod \quad M)\\
するとx,z,n,mはこう書けます。
n=n'-\frac{N}{2}\\
m=m'-\frac{M}{2}\\
x=\frac{L_x(-\frac{N}{2}+x')}{N}=-\frac{L_x}{2}+\frac{x'L_x}{N}\\
z=\frac{L_z(-\frac{M}{2}+z')}{M}=-\frac{L_z}{2}+\frac{z'L_z}{M}\\
続いて式簡略化のため${h'}$と$\tilde{h'}$を定義
{h'}({x'},{z'},t)=h(x,z,t)\\
\tilde{h'}(n',m',t)=\tilde{h}(\frac{2\pi n}{Lx},\frac{2\pi m}{Lz},t)\\
あとは求めたい$h()$についてゴリゴリ式変形すると
{h'}({x'},{z'},t)=h(x,z,t)=\sum_{m=-\frac{M}{2}}^{\frac{M}{2}-1}\sum_{n=-\frac{N}{2}}^{\frac{N}{2}-1}\tilde{h}(\frac{2\pi n}{Lx},\frac{2\pi m}{Lz},t)e^{i(\frac{2\pi n}{Lx}x+\frac{2\pi m}{Lz}z)}\\
=\sum_{m'=0}^{M-1}\sum_{n'=0}^{N-1}\tilde{h'}(n',m',t)e^{i(\frac{2\pi (n'-\frac{N}{2})}{Lx}x+\frac{2\pi (m'-\frac{M}{2})}{Lz}z)}\\
=\sum_{m'=0}^{M-1}\sum_{n'=0}^{N-1}\tilde{h'}(n',m',t)e^{
i(\frac{\pi N}{2}-\pi x'+\frac{2\pi n'(x'-N/2)}{N})+
i(\frac{\pi M}{2}-\pi z'+\frac{2\pi m'(z'-M/2)}{M})
}\\
ここでN,Mは256としていたので
e^{i(\frac{\pi N}{2})}=1\\
e^{i(\frac{\pi M}{2})}=1\\
なので消すことができ
e^{i (\frac{2\pi (x'+N/2)}{N})}=\\
e^{i (\frac{2\pi (x'-N/2) +2\pi N}{N})}=\\
e^{i (\frac{2\pi (x'-N/2)}{N})}=\\
e^{i (\frac{2\pi x''}{N})}\\
と置き換えられ
e^{i \pi}=-1
なのでまとめると
{h'}({x'},{z'},t)=
\sum_{m'=0}^{M-1}
\sum_{n'=0}^{N-1}
\tilde{h'}(n',m',t)e^{
i(\frac{\pi N}{2}-\pi x'+\frac{2\pi n'(x'-N/2)}{N})+
i(\frac{\pi M}{2}-\pi z'+\frac{2\pi m'(z'-M/2)}{M}) }\\
=(-1)^{x'}(-1)^{z'}\sum_{m'=0}^{M-1}\sum_{n'=0}^{N-1}\tilde{h'}(n',m',t)e^{
i(\frac{2\pi n'x''}{N})+
i(\frac{2\pi m'z''}{M})
}
あとは$x'$と$x''$を入れ替え、$z$も同様にして
{h'}({x''},{z''},t)\\
={h'}({x'}+\frac{N}{2} (mod N),{z'}+\frac{M}{2} (mod M),t)\\
=(-1)^{x''}(-1)^{z''}\sum_{m'=0}^{M-1}\sum_{n'=0}^{N-1}\tilde{h'}(n',m',t)e^{
i(\frac{2\pi n'x'}{N})+
i(\frac{2\pi m'z'}{M})
}
これでやっとよくある(?)FFTの形になりました。。。
普通と違うところは
・$h'$の添え字 : →計算結果の書き込み先を(N/2,M/2)ずらせばよい
・$(-1)^{x''}$と$(-1)^{z''}$ : →計算結果の書き込み先index x,zが(x+z)%2==1となる要素に-1をかければよい
ということでやはりよさそうです。
これらの要素を盛り込むことでこのようなコードになります。
ここでは横方向のfftと縦方向のfftを同じコードで実現しています。横方向を計算した後 縦方向を計算するので合計2回実行される前提のコードです。
#pragma kernel FFT2Dfunc256inv
#pragma kernel DFT2Dfunc256inv
#define PI 3.14159265358979323846264338328
RWStructuredBuffer<float2> buffer;//xが実数、yが虚数を格納
RWStructuredBuffer<float2> buffer_dmy;//xが実数、yが虚数を格納
//256*256要素の2D IFFT専用かつ負の周波数もあることも考慮しているコード(普通のFFT,DFTは正の周波数からはじまる)
//グループ数Nで実行されること前提
//2回実行されること前提
#define M (8)
#define N (1<<M)
groupshared float2 block[N];
[numthreads(N/2, 1, 1)]
void FFT2Dfunc256inv(uint id : SV_DispatchThreadID, uint grid : SV_GroupID, uint gi : SV_GroupIndex)
{
block[gi * 2] = buffer[grid * N + gi * 2];
block[gi * 2 + 1] = buffer[grid * N + gi * 2 + 1];
for (int loopidx = 0; loopidx < M; loopidx++)
{
int dleng = 1 << (M - loopidx - 1);
uint t = gi % dleng;
uint t0 = (gi / dleng) * dleng * 2 + t;
uint t1 = t0 + dleng;
GroupMemoryBarrierWithGroupSync();
float r1 = block[t1].x;
float i1 = block[t1].y;
float r0 = block[t0].x - r1;
float i0 = block[t0].y - i1;
float rad = PI * t / dleng;//invなので-がかかっている
float fsin = sin(rad);
float fcos = cos(rad);
block[t0].x += r1;
block[t0].y += i1;
block[t1].x = r0 * fcos - i0 * fsin;
block[t1].y = r0 * fsin + i0 * fcos;
}
GroupMemoryBarrierWithGroupSync();
float2 reim0 = block[reversebits(gi * 2) >> (32 - M)];//32はuint=32bitの32
float2 reim1 = block[reversebits(gi * 2 + 1) >> (32 - M)];
reim1 = -reim1;//出力結果に(-1)^indexが乗算されるので
//書き込みはx,yを転置している。これによって2D FFTの計算の1回目と2回目を同じコードにできて、かつ、最終的なメモリ配置は最初と同じに戻る
//最終的な書き込み先をN/2,N/2ずらすのも忘れずに
buffer_dmy[(gi * 2 + N / 2) % N * N + grid] = reim0;
buffer_dmy[(gi * 2 + 1 + N / 2) % N * N + grid] = reim1;
}
//DFTで愚直に書いたバージョン
//デバッグ用、理解を深める用
//グループ数Nで実行されること前提
[numthreads(N, 1, 1)]
void DFT2Dfunc256inv(uint id : SV_DispatchThreadID, uint grid : SV_GroupID, uint gi : SV_GroupIndex)
{
int x = gi - N / 2;
int z = grid - N / 2;
float2 dftsum = 0;
for (int j = 0; j < N; j++)
{
int kz = -N / 2 + j;//* (2.0f * PI / N);
for (int i = 0; i < N; i++)
{
int kx = -N / 2 + i;// *(2.0f * PI / N);
float rad = ((kx * x + kz * z) % N) * (2.0f * PI / N);
float2 h = buffer[j * N + i];
dftsum.x += h.x * cos(rad) - h.y * sin(rad);
dftsum.y += h.y * cos(rad) + h.x * sin(rad);
}
}
buffer_dmy[id] = dftsum;
}
Dispatch側のコード
using UnityEngine;
public class FFT : MonoBehaviour
{
const bool DEBUG = false;
[SerializeField] ComputeShader shader;
ComputeBuffer buffer_dbg;
int kernel_FFT2Dfunc256inv, kernel_DFT2Dfunc256inv;
void Awake()
{
kernel_FFT2Dfunc256inv = shader.FindKernel("FFT2Dfunc256inv");
kernel_DFT2Dfunc256inv = shader.FindKernel("DFT2Dfunc256inv");
}
void Start()
{
if (DEBUG) buffer_dbg = new ComputeBuffer(1, sizeof(float) * 2);
}
//bufferが入力、FFTの結果がbufferに出力
public void FFT2D_256_Dispatch(ComputeBuffer buffer, ComputeBuffer buffer_dmy)
{
if (DEBUG) DEBUG_func1(buffer);
//①引数をセット
shader.SetBuffer(kernel_FFT2Dfunc256inv, "buffer", buffer);
shader.SetBuffer(kernel_FFT2Dfunc256inv, "buffer_dmy", buffer_dmy);
// GPUで計算
shader.Dispatch(kernel_FFT2Dfunc256inv, 256, 1, 1);
//②引数をセット
shader.SetBuffer(kernel_FFT2Dfunc256inv, "buffer", buffer_dmy);
shader.SetBuffer(kernel_FFT2Dfunc256inv, "buffer_dmy", buffer);
// GPUで計算
shader.Dispatch(kernel_FFT2Dfunc256inv, 256, 1, 1);
if (DEBUG) DEBUG_func2(buffer);
}
//bufferが入力、FFTの結果がbuffer_dmyに出力
public void DFT2D_256_Dispatch(ComputeBuffer buffer, ComputeBuffer buffer_dmy)
{
//引数をセット
shader.SetBuffer(kernel_DFT2Dfunc256inv, "buffer", buffer);
shader.SetBuffer(kernel_DFT2Dfunc256inv, "buffer_dmy", buffer_dmy);
// GPUで計算
shader.Dispatch(kernel_DFT2Dfunc256inv, 256, 1, 1);
}
//FFTとDFTを比較
void DEBUG_func1(ComputeBuffer buffer)
{
if (buffer_dbg.count!= buffer.count)
buffer_dbg = new ComputeBuffer(buffer.count, sizeof(float) * 2);
DFT2D_256_Dispatch(buffer, buffer_dbg);
}
//FFTとDFTを比較
void DEBUG_func2(ComputeBuffer buffer)
{
Vector2[] bfr = new Vector2[buffer.count];
Vector2[] bfr_dbg = new Vector2[buffer.count];
buffer.GetData(bfr);
buffer_dbg.GetData(bfr_dbg);
float rss = 0.0f;
for(int i=0;i< buffer.count;i++)
{
Vector2 v2 = bfr[i] - bfr_dbg[i];
rss += v2.sqrMagnitude;
}
Debug.Log(rss);
}
}
カーネルプログラムFFT2Dfunc256invはコメントにもあるよう
・iFFTを普通に計算し(Cooley-Tukeyなので最後にbit逆順がある)
・書き込み先indexが奇数なら-1をかけ
・N/2ずらして
・行列転置(縦横入れ替え)してメモリに書き込み
しています。
文字だけだとわかりにくいのでプログラムの動作を画像化してみました。カラーが最初のメモリの位置に相当します。色味が落ちてるところは-1がかかっているという意味です。
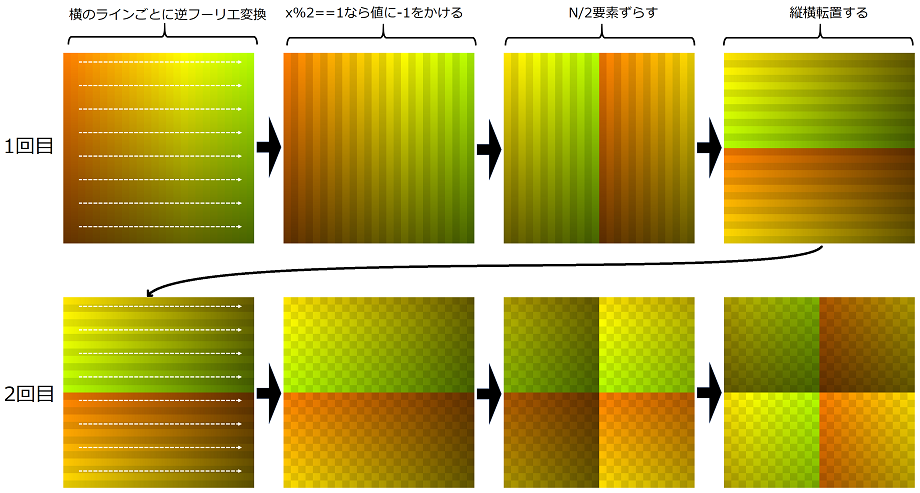
これによって
・計算結果全体を(N/2,N/2)ずらす
・要素のindex x,zが(x+z)%2==1となる要素に-1をかける
が実現していることがわかります。
4.右の画像から実際の位置にレンダリング
いろいろ大変な実装でしたが画面に描画してうまくいったとき疲れが全部吹き飛びます!あと一歩です。
すでに高さ情報はComputeBufferに格納されているので
Graphics.DrawProceduralNow
などで手軽に描画することができます。一番簡単なPointsの描画をしてみます。
CPU側コードとShaderはこんなかんじ
using UnityEngine;
public class FFTOceanMain : MonoBehaviour
{
[SerializeField] ComputeShader shader;
[SerializeField] Shader renderingShader;
Material renderingShader_Material;
[SerializeField] FFT fFT;
[SerializeField] Phillips phillips;
int kernel_GenerateSpectrumKernel;
Vector2[] h_h0;
public ComputeBuffer d_h0, d_ht, d_ht_dmy;
int cnt;
private void Awake()
{
kernel_GenerateSpectrumKernel = shader.FindKernel("GenerateSpectrumKernel");
renderingShader_Material = new Material(renderingShader);
cnt = 0;
}
void Start()
{
h_h0 = phillips.Generate_h0();//CPU側メモリ確保。サイズはsizeof(Vector2)*256*256
d_h0 = new ComputeBuffer(h_h0.Length, sizeof(float) * 2);//GPU側メモリ確保 サイズはsizeof(Vector2)*256*256
d_ht = new ComputeBuffer((int)(Phillips.meshSize * Phillips.meshSize), sizeof(float) * 2);//GPU側メモリ確保 サイズはsizeof(Vector2)*256*256
d_ht_dmy = new ComputeBuffer(d_ht.count, sizeof(float) * 2);
d_h0.SetData(h_h0);
SetArgs();
}
void SetArgs()
{
//ComputeShader引数をセット
shader.SetBuffer(kernel_GenerateSpectrumKernel, "h0", d_h0);
shader.SetBuffer(kernel_GenerateSpectrumKernel, "ht", d_ht);
shader.SetInt("N", (int)Phillips.meshSize);
shader.SetInt("seasizeLx", (int)Phillips.seasizeLx);
shader.SetInt("seasizeLz", (int)Phillips.seasizeLz);
// GPUバッファをマテリアルに設定
renderingShader_Material.SetBuffer("d_ht", d_ht);
// その他Shader 定数関連
renderingShader_Material.SetInt("N", (int)Phillips.meshSize);
renderingShader_Material.SetFloat("halfN", 0.5f * Phillips.meshSize);
renderingShader_Material.SetFloat("dx", 1.0f * Phillips.seasizeLx / Phillips.meshSize);
renderingShader_Material.SetFloat("dz", 1.0f * Phillips.seasizeLz / Phillips.meshSize);
}
void Update()
{
//引数をセット
shader.SetFloat("t", 0.03f * cnt);
shader.Dispatch(kernel_GenerateSpectrumKernel, 1, 256, 1);//d_h0からd_htを計算
fFT.FFT2D_256_Dispatch(d_ht, d_ht_dmy);//d_htから高さデータを計算
cnt++;
}
void OnRenderObject()
{
// レンダリングを開始
renderingShader_Material.SetPass(0);
// n個のオブジェクトをレンダリング
Graphics.DrawProceduralNow(MeshTopology.Points, 256 * 256);
}
private void OnDestroy()
{
//解放
d_h0.Release();
d_ht.Release();
d_ht_dmy.Release();
}
}
Shader "Custom/SurfaceShader" {
SubShader{
Pass {
CGPROGRAM
// シェーダーモデルは5.0を指定
#pragma target 5.0
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
StructuredBuffer<float2> d_ht;
uint N;
float halfN;
float dx;
float dz;
float4 ui_calcPos(uint ui_idx)
{
uint x = ui_idx % N;
uint z = ui_idx / N;
float2 h = d_ht[ui_idx];
return float4((1.0 * x - halfN) * dx, h.x, (1.0 * z - halfN) * dz, 1);
}
struct VSOut {
float4 pos : SV_POSITION;
};
// 頂点シェーダ
VSOut vert(uint id : SV_VertexID)
{
VSOut output;
output.pos = ui_calcPos(id);
output.pos = mul(UNITY_MATRIX_VP, output.pos);
return output;
}
// ピクセルシェーダー
fixed4 frag(VSOut i) : COLOR
{
return float4(0,1,1,1);
}
ENDCG
}
}
}
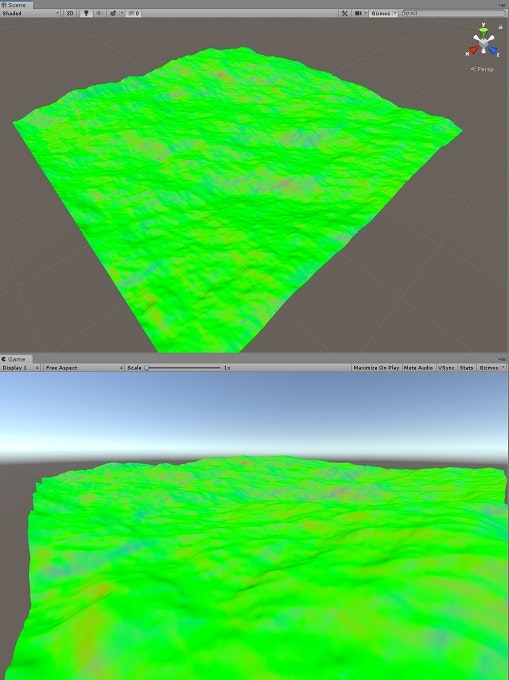
実行結果

これだけでも十分綺麗ですね~!
ここまでのコードは
github
https://github.com/toropippi/OceanFFT/tree/main/OceanFFT1_points
にUPしてます。
法線を計算
さてせっかく綺麗な絵が出そうな雰囲気なので法線も計算してみましょう。
中心差分で算出
お手軽な方法として、すでに計算してある海面の高さを利用して中心差分で勾配を計算します。
x,z方向の勾配が求まれば、海面と垂直なベクトルがでます。
\vec{N}=normalize(-xの傾き,1,-zの傾き)
この計算のところだけピックアップします。雰囲気だけでもわかってもらえれば幸いです。
uint x0 = (id.x - 1 + N) % N;
uint x1 = (id.x + 1) % N;
uint y0 = (id.y - 1 + N) % N;
uint y1 = (id.y + 1) % N;
float subx = 0.5f * (ht[x1 + id.y * N].x - ht[x0 + id.y * N].x) * rdx;
float subz = 0.5f * (ht[id.x + y1 * N].x - ht[id.x + y0 * N].x) * rdz;
float3 vec = normalize(float3(-subx, 1.0, -subz));
float4 out4 = 1;
out4.xyz = vec;
tex[id] = out4;
法線ベクトル情報x,y,zをr,g,bで出力
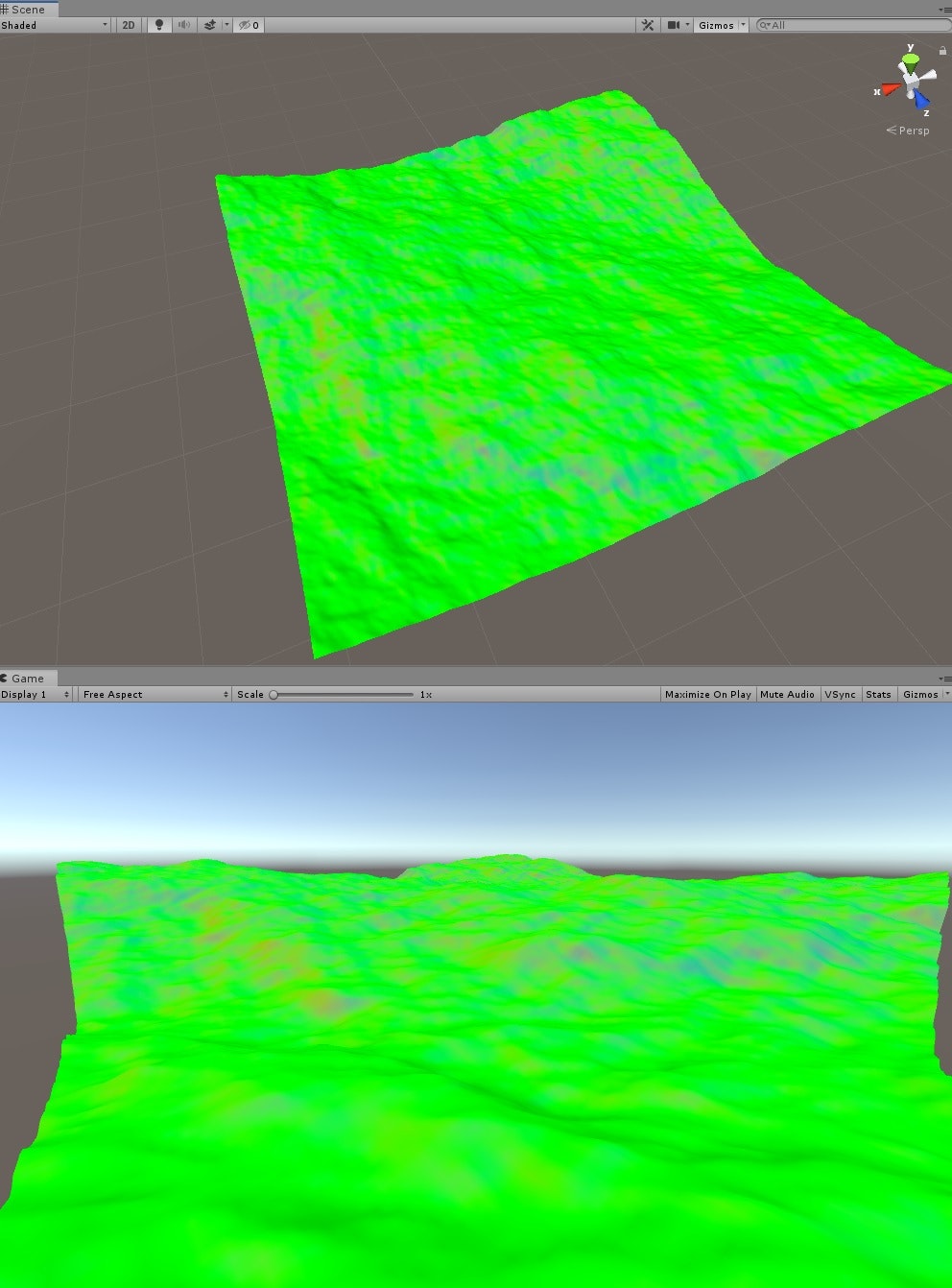
できました。あとは煮るなり焼くなり法線情報でうまくライティングすればきれいな絵ができるでしょう。
github
https://github.com/toropippi/OceanFFT/tree/main/OceanFFT2_normal
念のためですが、法線が本当に正しいか、Aを100倍にして出力してみました。
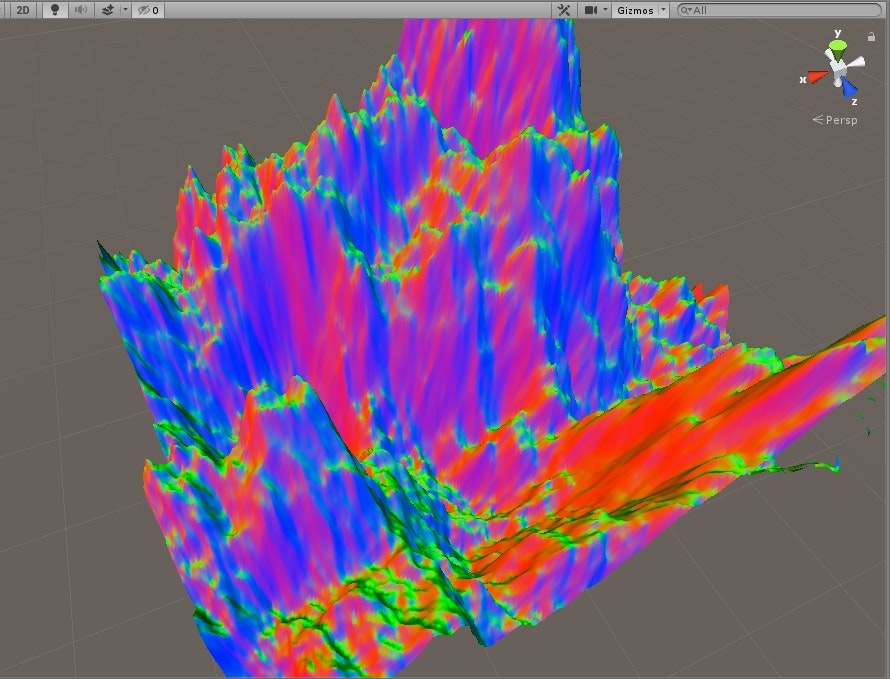
x方向に向いている面は赤く、z方向に向いている面は青くなっています。面の法線ベクトルのx,z成分がr,bに対応しているので正しそうです。
偏微分で解析的に算出
ところでせっかく難しい式を計算をしてスペクトルを出してきたので、法線も式から求められないでしょうか。
これも結論から言うとできます。
これで偏微分が計算できます。
\nabla h(\vec{x},t)=\sum_{\vec{k}}i\vec{k}\tilde{h}(\vec{k},t)e^{i\vec{k}\cdot \vec{x}}
$\tilde{h}(\vec{k},t)$は「2.それをベースに毎フレームh(k,t)をGPU上で生成」で求めたやつです。これに$i\vec{k}$がかかっていますが、各要素の計算時に求めていた$kx,kz$を使うだけです。
x方向の偏微分ならkxをz方向の偏微分ならkzのみを使います。
...............................
[numthreads(256, 1, 1)]
void GenerateSpectrumKernel(uint2 id : SV_DispatchThreadID)
{
uint x = id.x;
uint y = id.y;
uint in_index = y * N + x;
uint in_mindex = (N - y) % N * N + (N - x) % N; // mirrored
uint out_index = y * N + x;
// calculate wave vector
float2 k;
k.x = (-(int)N / 2.0f + x) * (2.0f * PI / seasizeLx);
k.y = (-(int)N / 2.0f + y) * (2.0f * PI / seasizeLz);
// calculate dispersion w(k)
float k_len = sqrt(k.x * k.x + k.y * k.y);
float w = sqrt(9.81f * k_len);
float2 h0_k = h0[in_index];
float2 h0_mk = h0[in_mindex];
// output frequency-space complex values
float2 htval = complex_add(complex_mult(h0_k, complex_exp(w * t)), complex_mult(conjugate(h0_mk), complex_exp(-w * t)));
ht[out_index] = htval;//普通の高さの逆フーリエ前
float2 htival;//i*htval
htival.x = -htval.y;
htival.y = htval.x;
ht_dx[out_index] = htival * k.x; //x方向偏微分の逆フーリエ前
ht_dz[out_index] = htival * k.y; //z方向偏微分の逆フーリエ前
}
そしてそれを逆フーリエ変換することで海面の高さの勾配(偏微分)が求まります。ここで、手元には複素数の状態で結果があると思いますが、使うのは実数成分のみです。海面の高さには実数のみを使用しているので勾配情報も実数のみを使う必要があります。
あとはさっきと同じように法線を計算し
できました。
さっきと見た目かわんないですが、中心差分よりは精度よくできてると思います。
これもgithubにupしてるので参考にしてください。
github
https://github.com/toropippi/OceanFFT/tree/main/OceanFFT3_analyticalNormal
もうちょっとライティングを頑張る
正直Compute Shader以外のシェーダーやレンダリングは詳しくないのでたいしたことは書けません。
一応、法線から反射ベクトルを計算してフレネル反射とか実装したりしなかったり・・・
コードを見ればわかりますが視線ベクトル決め打ちのレイトレーシングみたいなことをしています、、、だからカメラ動かしても絵は変わらないというひどいコード。誰かレンダリング教えて・・・

github
https://github.com/toropippi/OceanFFT/tree/main/OceanFFT4lighting
まぁかつてないほど海っぽくなったのでいいでしょう。
Choppy wave
NVIDIAのスライドを見るに、さっきの偏微分にすごい似た、でもちょっと違う式で計算されたDx,Dyというのを求めています。これは法線を計算するためのものではなく、波をより尖らせたChoppy waveを作るために必要なようです。

今までの波はあくまで有限個のsin,cosの足し合わせでできた波で、ちょっと滑らかになりすぎてるという問題があったようです。それをアーティスティックな謎テクで解決するのが今から説明する方法です。
いや滑らかすぎるならもっと離散点を増やして細かいsin,cosを足し合わせばいいじゃないかと個人的には思いましたが、そう書いてあるので仕方ありません。
まぁおそらく離散点を増やすと計算負荷が上がるからダメなんでしょうね。
Choppy waveの計算手順はというと、まずDx,Dyを計算します。数式では $\vec{D}$ と書いてあります。
\vec{D}(\vec{x},t)=\sum_{\vec{k}}-i\frac{\vec{k}}{k}\tilde{h}(\vec{k},t)e^{i\vec{k}\cdot \vec{x}}\\
\vec{x}'=\vec{x}+\lambda \vec{D}(\vec{x},t)
そしてこの$\vec{x}'$を新しい座標として使います。
今まで$\vec{x}=(x,z)$としてx,z座標は固定でやってきてましたよね。でy座標だけが動いていたと。
今度は$\lambda$に2.0とか-3.4とか適当な値をいれることでx,zもリアルタイムに動いて、見た目が激しくなるというイメージです。
\vec{D}(\vec{x},t)=\sum_{\vec{k}}-i\frac{\vec{k}}{k}\tilde{h}(\vec{k},t)e^{i\vec{k}\cdot \vec{x}}\\
の求め方ですが、偏微分を求めるときに書いたコードにちょっと付け足すだけです。
..................
[numthreads(256, 1, 1)]
void GenerateSpectrumKernel(uint2 id : SV_DispatchThreadID)
{
uint x = id.x;
uint y = id.y;
uint in_index = y * N + x;
uint in_mindex = (N - y) % N * N + (N - x) % N; // mirrored
uint out_index = y * N + x;
// calculate wave vector
float2 k;
k.x = (-(int)N / 2.0f + x) * (2.0f * PI / seasizeLx);
k.y = (-(int)N / 2.0f + y) * (2.0f * PI / seasizeLz);
// calculate dispersion w(k)
float k_len = sqrt(k.x * k.x + k.y * k.y);
float w = sqrt(9.81f * k_len);
float2 h0_k = h0[in_index];
float2 h0_mk = h0[in_mindex];
// output frequency-space complex values
float2 htval = complex_add(complex_mult(h0_k, complex_exp(w * t)), complex_mult(conjugate(h0_mk), complex_exp(-w * t)));
ht[out_index] = htval;//普通の高さの逆フーリエ前
float2 htival;//i*htval
htival.x = -htval.y;
htival.y = htval.x;
ht_dx[out_index] = htival * k.x; //x方向偏微分の逆フーリエ前
ht_dz[out_index] = htival * k.y; //z方向偏微分の逆フーリエ前
if (k_len != 0.0)
{
k.x /= k_len;
k.y /= k_len;
}
displaceX[out_index] = -htival * k.x; //Dxの逆フーリエ前
displaceZ[out_index] = -htival * k.y; //Dyの逆フーリエ前
}
これで
-i\frac{\vec{k}}{k}\tilde{h}(\vec{k},t)
の部分まで求まったので、あとは3の手順でiFFTして完成です。
数式のお気持ちを考える
これで新しい座標$\vec{x}'$を求めることができましたが、これがどんな意味があるのか少し考えてみましょう。
上でも書いたよう、$\vec{D}(\vec{x},t)$の式は偏微分の式に酷似しています。
\nabla h(\vec{x},t)=\sum_{\vec{k}}i\vec{k}\tilde{h}(\vec{k},t)e^{i\vec{k}\cdot \vec{x}}\\
\vec{D}(\vec{x},t)=\sum_{\vec{k}}-i\frac{\vec{k}}{k}\tilde{h}(\vec{k},t)e^{i\vec{k}\cdot \vec{x}}\\
違うのはマイナスがかかっていることと、ベクトルの長さkで割っているところです。
kで割っても正負は反転しないのでここはざっくり"(偏微分×-1)に近い値"として思考を進めてみます。
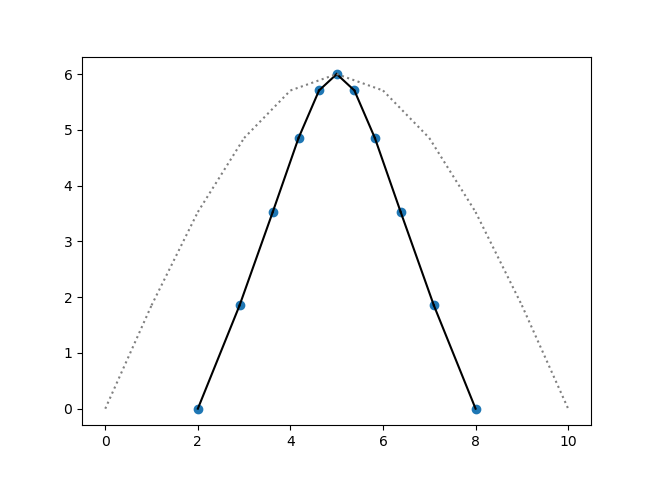
簡単に1次元として、x座標を移動させるということは、こんな形の波があったときに青丸が矢印の方向に移動することが想像できます。
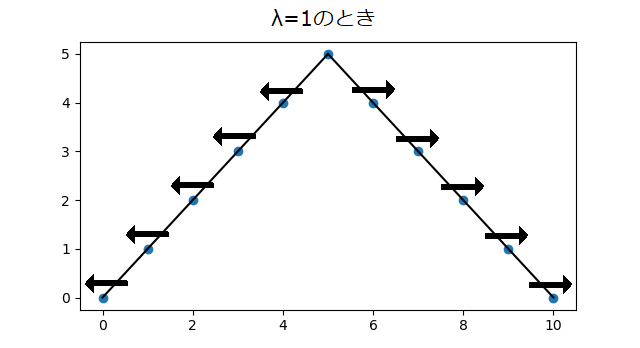
ということは移動後は
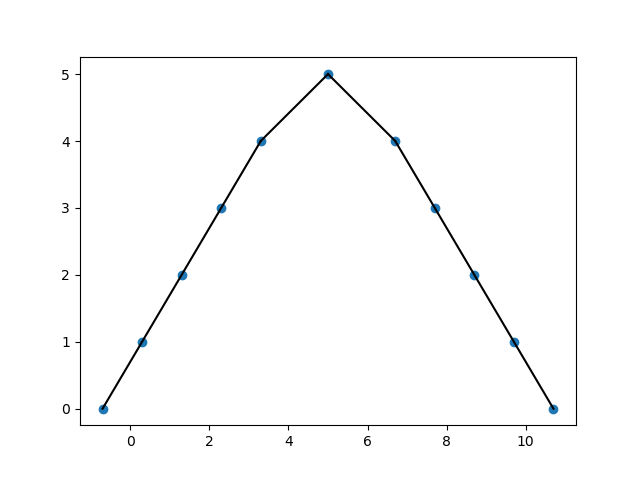
となります。あれ、波が尖がるどころかなだらかになってるじゃないか・・・
次sinカーブでも同じように考えてみます。
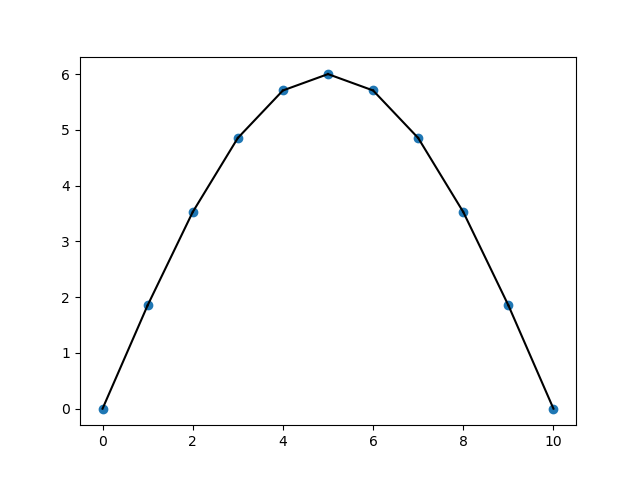
これが$\lambda=1$のとき
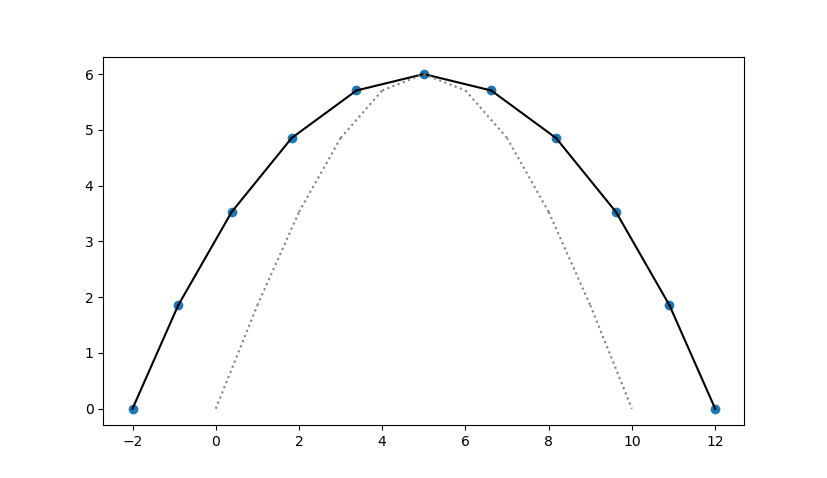
やっぱりなだらかになってる。
これが正解では???
λをいじって最適なChoppy waveを作る
実は論文にもほかの参考になりそうなサイトにも、λの決め方についてほとんどなにも書かれていません。まぁ適当にいじって決めてねってことなんだと思いますが、数式のお気持ちを察するに、これはマイナスの値を入れないといけないのではないでしょうか。
実際にやってみました。
λ=0.0のとき
λ=2.0のとき
λ=-2.0のとき
λ=9.0のとき
λ=-9.0のとき
やっぱり
λはマイナスの数字を入れることで波を尖がらせることができ、プラスの値をいれると滑らかにすることができます。と私は理解しています。
法線を修正
さて、x,zの位置がずれたことで海面の傾きが変わったので法線も今までの値を使うことはできません。
今のところchoppy waveを実装して海面の法線をまじめに計算しているコードは中国語の https://zhuanlan.zhihu.com/p/96811613 ここで紹介されてる https://github.com/Straw1997/FFTOcean にupされてるコードしか確認できませんでした (探せばほかにもあるかもしれませんが)。
この方のコードをみると、x,z座標を動かあした後 中心差分で求めているようでした。しかしそもそも海面の高さをhtの実数じゃなくて複素数の絶対値で求めていたり、ちょっと私のやり方とは違うので参考にはできませんでした。
そこで私オリジナルのやり方になりますが、下記のような方法で実装してみました。
#pragma kernel SetNormal
RWTexture2D<float4> tex;
RWStructuredBuffer<float2> ht_dx;
RWStructuredBuffer<float2> ht_dz;
RWStructuredBuffer<float2> displaceX;
RWStructuredBuffer<float2> displaceZ;
uint N;
float dx;
float dz;
float lambda;
[numthreads(256, 1, 1)]
void SetNormal(uint2 id : SV_DispatchThreadID)
{
uint x0 = (id.x - 1 + N) % N;
uint x1 = (id.x + 1) % N;
uint y0 = (id.y - 1 + N) % N;
uint y1 = (id.y + 1) % N;
float subx = ht_dx[id.x + id.y * N].x;
float subz = ht_dz[id.x + id.y * N].x;
//displaceXZだけ定義点が移動することを考えここで傾きをさらにいじる
subx *= 2.0 * dx / ((displaceX[x1 + id.y * N].x - displaceX[x0 + id.y * N].x) * lambda + 2.0 * dx);
subz *= 2.0 * dz / ((displaceZ[id.x + y1 * N].x - displaceZ[id.x + y0 * N].x) * lambda + 2.0 * dz);
float3 vec = normalize(float3(-subx, 1.0, -subz));
float4 out4 = 1;
out4.xyz = vec;
tex[id] = out4;
}
考え方としてはこんな感じ。解説図では$\lambda=1$として省略してます。
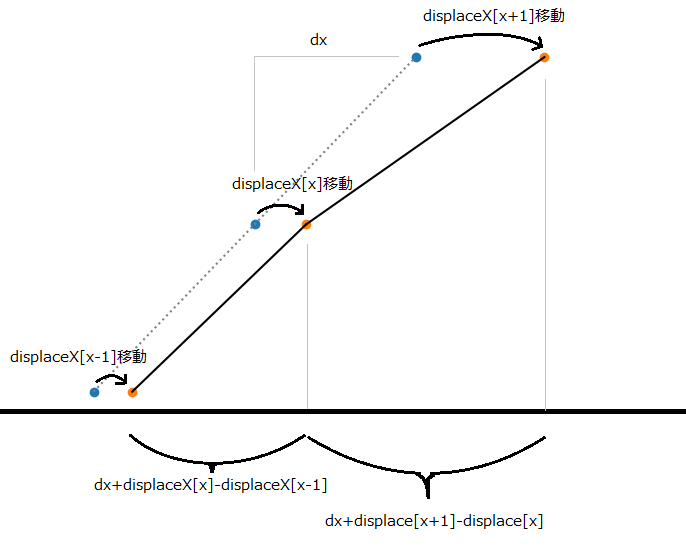
displaceXの分だけ点が動いて線の傾きかたが圧縮、拡張されるというイメージです。
これらを適応して$\lambda=-2$としたコードがこちら。
github
https://github.com/toropippi/OceanFFT/tree/main/OceanFFT5ChoppyWave
ま、十分綺麗なのでいいでしょう。
ここで、波のポリゴンが交差してるのが見えるでしょうか。画面左と、左奥の2か所です。これがchoppy waveの恩恵で、今回の実装で相当リアルになってきたのがわかると思います。
実際自分も実装していて、この絵が作れた時はかなりテンションあがりました。それまでは確かにのぺっとしていて、ちょっとおかしいなって感じはありました。
ここまでくるとFFT Oceanの実装で一番重要なのってここなんじゃ・・・?とすら思います。
泡表現(bubbles)
さっき波ポリゴンが重なるといいましたが、今度はこの重なりを検出して泡を表現しようという話です。
この検出にも$\vec{D}(\vec{x},t)$を使います。(プログラムでいうとdisplaceX,displaceZ)
J=J_{xx}J_{zz}-J_{xz}J_{zx}\\
J_{xx}=1+\lambda\frac{\partial D_x(\vec{x},t)}{\partial x}\\
J_{zz}=1+\lambda\frac{\partial D_z(\vec{x},t)}{\partial z}\\
J_{xz}=\lambda\frac{\partial D_x(\vec{x},t)}{\partial z}\\
J_{zx}=\lambda\frac{\partial D_z(\vec{x},t)}{\partial x}\\
このJの正負がマイナスのとき、その場所で重なり(反転)が起きていることになります。
したがってこんなコードになります。
#pragma kernel SetNormalBubble
RWTexture2D<float4> normalTex;
RWTexture2D<float> bubbleTex;
RWStructuredBuffer<float2> ht_dx;
RWStructuredBuffer<float2> ht_dz;
RWStructuredBuffer<float2> displaceX;
RWStructuredBuffer<float2> displaceZ;
uint N;
float dx;
float dz;
float lambda;
[numthreads(256, 1, 1)]
void SetNormalBubble(uint2 id : SV_DispatchThreadID)
{
uint x0 = (id.x - 1 + N) % N;
uint x1 = (id.x + 1) % N;
uint y0 = (id.y - 1 + N) % N;
uint y1 = (id.y + 1) % N;
float dDxdx = 0.5 * (displaceX[x1 + id.y * N].x - displaceX[x0 + id.y * N].x);//中心差分
float dDzdz = 0.5 * (displaceZ[id.x + y1 * N].x - displaceZ[id.x + y0 * N].x);//中心差分
float dDxdz = 0.5 * (displaceX[id.x + y1 * N].x - displaceX[id.x + y0 * N].x);//中心差分
float dDzdx = 0.5 * (displaceZ[x1 + id.y * N].x - displaceZ[x0 + id.y * N].x);//中心差分
float gradx = ht_dx[id.x + id.y * N].x;
float gradz = ht_dz[id.x + id.y * N].x;
//displaceXZだけ定義点が移動することを考えここで傾きをさらにいじる
gradx *= dx / (dDxdx * lambda + dx);
gradz *= dz / (dDzdz * lambda + dz);
float3 vec = normalize(float3(-gradx, 1.0, -gradz));
float4 out4 = 1;
out4.xyz = vec;
normalTex[id] = out4;
//Jの計算
float Jxx = 1.0 + dDxdx * lambda;
float Jzz = 1.0 + dDzdz * lambda;
float Jxz = dDxdz * lambda;
float Jzx = dDzdx * lambda;
float J = Jxx * Jzz - Jxz * Jzx;//J<0なら面が裏返しになってる
bubbleTex[id] = J;
}
レンダリング側
Shader "Custom/SurfaceShader" {
Properties{
_MainTexN("-" , 2D) = "black" {}
_MainTexB("-" , 2D) = "black" {}
}
SubShader{
Pass {
CGPROGRAM
// シェーダーモデルは5.0を指定
#pragma target 5.0
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
sampler2D _MainTexN;
sampler2D _MainTexB;
StructuredBuffer<float2> d_ht;
StructuredBuffer<float2> d_displaceX;
StructuredBuffer<float2> d_displaceZ;
uint N;
float halfN;
float dx;
float dz;
float lambda;
float Get_d_ht_real(uint x,uint z)
{
float2 h = d_ht[x % 256 + z % 256 * 256];
return h.x;
}
float2 Get_d_displaceXZ(uint x, uint z)
{
float2 ret;
ret.x = d_displaceX[x % 256 + z % 256 * 256].x;
ret.y = d_displaceZ[x % 256 + z % 256 * 256].x;
return lambda * ret;
}
struct VSOut {
float4 pos : SV_POSITION;
float3 pos2 : TEXCOORD2;
float2 uv : TEXCOORD0;
};
// 頂点シェーダ、1つの4角形ポリゴンに頂点4つ
VSOut vert(uint id : SV_VertexID,float3 normal : NORMAL)
{
VSOut output;
uint sqx = ((id + 1) % 4 / 2);//連続するid4つで四角形を作る
uint sqz = (1 - id % 4 / 2);
sqx += (id / 4) % 256;
sqz += (id / 4) / 256;
output.pos.y = Get_d_ht_real(sqx, sqz);
output.pos.xz = float2((sqx - halfN) * dx, (sqz - halfN) * dz);//4角形
output.pos.xz += Get_d_displaceXZ(sqx, sqz);
output.pos.w = 1;
output.pos2 = output.pos.xyz;
output.pos = mul(UNITY_MATRIX_VP, output.pos);
float rN1 = 1.0 / N;
output.uv = float2(sqx, sqz) * rN1 + float2(0.5, 0.5) * rN1;
return output;
}
// ピクセルシェーダー
// ワールド座標系がよくわからないのでレイトレーシング的に色を決定している(要修正)
float4 frag(VSOut i) : COLOR
{
float4 col; col.w = 1;
float3 normal = normalize(tex2D(_MainTexN, i.uv).xyz);//線形補完されて単位ベクトルじゃなくなっているので
float3 viewDir = normalize(i.pos2 - float3(0, 41, -330));//ここはMain Cameraの座標を埋め込み
float3 lightDir = normalize(float3(0.15, 0.45, 0.6));//ライトベクトルも埋め込み
float3 reflectDir = -2.0 * dot(normal, viewDir) * normal + viewDir;
float v = dot(reflectDir, lightDir);
float3 sky = (v + 1.0) * float3(105.0 / 256, 133.0 / 256, 184.0 / 256);//空の色も埋め込み、しかも単色
float fresnel = (0.05 + (1 - 0.05) * pow(1 - max(dot(normal, -viewDir),0), 5));
col.xyz = sky * fresnel + (1.0 - fresnel) * float3(0.01, 0.13, 0.15);//海の色も埋め込み
col.xyz += pow(max(v, 0), 649) * float3(1.2, 1.0, 0.86);//太陽の色も埋め込み
//泡
float bubble = tex2D(_MainTexB, i.uv);
if (bubble < -0.3) {
bubble = min(-bubble * 0.4, 1);//裏返り度合いに応じて徐々に白くなる
col.xyz = bubble * float3(1.0, 1.0, 1.0) + (1.0 - bubble) * col.xyz;
}
return col;
}
ENDCG
}
}
}
結果
github
https://github.com/toropippi/OceanFFT/tree/main/OceanFFT6Bubbles
波のてっぺん付近が白く着色されているのがわかります。波の先端、特にとがっているところは海面が90度以上傾いていることがあります。それを先ほどの計算で検出し、泡としてレンダリングしたということになります。
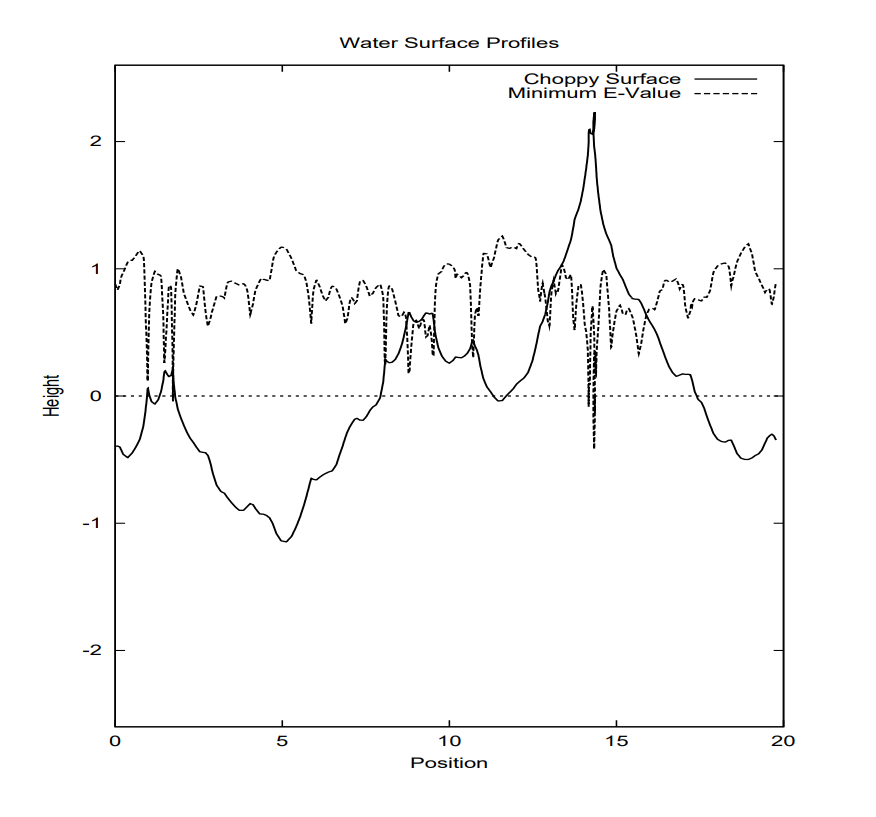
論文のFigureがわかりやすいかなと思ったのですが、Choppy Surfaceと書いてある波はよく目を凝らしてみるとPosition=15付近でぐるっと回っているのがわかります。これに対しMinimum E-value(最小固有値)がそこで0を下回っているというのが読み取れます。
論文では、最大固有値は常に正で最小固有値は図のように負になるから、最大固有値×最小固有値がマイナスなのを確認できれば検出できるよねと言ってます。プログラムでは$Jxx,Jxz,Jzx,Jzz$の2*2の行列の行列式を求めることで、この最大固有値×最小固有値がマイナスかどうかを判定しています。(というか参考にしたコードがそういうコードだった)
正直、実装量に対して見ための効果は薄く、費用対効果は Choppy Wave>泡表現 なのでここは飛ばしてもいいかもしれません。
おしまい
残った課題を箇条書きで
・Shaderの要修正の部分はそのうち修正してgithubに
・泡のレンダリングもうちょっと頑張れるはず
・Donelan-Banner調べる
・海面をループさせて無限海面に、遠くはLODで
解決した課題を箇条書きで
・FFTの計算部分は2倍高速化できる。海面の高さはFFTの計算結果のうち実数しか使わないので、実数FFTの逆の手順を行うことで1/2のサイズのFFTで済む。円周率.jpの実数FFTの説明を参考に複素数→実数FFTのC++コードを書いたのでこれを参考に。ただ並列化しにくい部分があるのでComputeShaderへの適応はよく考える必要がある。
参考文献
一番参考にした中国語の解説
https://zhuanlan.zhihu.com/p/96811613
https://zhuanlan.zhihu.com/p/64414956
https://zhuanlan.zhihu.com/p/95482541
https://github.com/Straw1997/FFTOcean
NV_OceanCS_Slides
http://www-evasion.imag.fr/~Fabrice.Neyret/images/fluids-nuages/waves/Jonathan/articlesCG/NV_OceanCS_Slides.pdf
UE4で海面シミュレーションと描画を行う at Qiita
https://qiita.com/monguri/items/3ad184c3316343c635f5
その他英語スライドなど
http://developer.download.nvidia.com/assets/gameworks/downloads/regular/events/cgdc15/CGDC2015_ocean_simulation_en.pdf
http://evasion.imag.fr/~Fabrice.Neyret/images/fluids-nuages/waves/Jonathan/articlesCG/waterslides2001.pdf
https://www.slideshare.net/Codemotion/an-introduction-to-realistic-ocean-rendering-through-fft-fabio-suriano-codemotion-rome-2017
参考にしたコード
https://github.com/nobnak/FftUnity
https://github.com/gasgiant/FFT-Ocean