はじめに
個人的な事情により使用言語をC++からPythonに変更した。C++の解説はAtcoder公式をはじめ、最もメジャーで多くの人が既に解説している。今回からはコード量が少なく簡潔にコーディングできるだけでなく、ライブラリも充実しているPythonを用いる。
1. 267-C問題
問題
長さ $N$ の整数列 $A = (A_1,A_2,...,A_N)$ が与えられる。
長さ$M$ の$A$ の連続部分列$B = (B_1,B_2,...,B_M)$ に対する $\sum_{i=1}^{M} iB_i$ の最大値を求めよ。
制約
$1\leq M\leq N\leq 2 \times 10^5 $
$-2 \times 10^5 \leq A_i \leq 2 \times 10^5 $
解法
整数列$A$の部分列は全部で$N-M+1$通り、部分列の文字数は$M$となり線形探索を行うと計算量は$O(N(N-M+1)) = O(N^2)$ となりTLE(実行時間制限オーバー)となってしまう。よって何かしらの工夫を施す必要があるとこの時点で分かる。
注目すべき点は部分列は連続であること、そして乗ずる自然数が等差型になっていることである。高校数学の数学Bで数列という単元がある。その中に等差×等比型の数列の一般項を求める有名な解法がある。この解法に近いことをする。
$S_n = 1\times1 + 2\times r + 3 \times r^2 + ...+ n \times r^{n-1} ・・・⓵$
$rS_n = \qquad1\times r + 2\times r^2 + 3 \times r^3 + ...+ (n-1) \times r^{n-1} + n \times r^n ・・・⓶$
$①-②$
$(1-r)S_n = 1 + r + r^2 + r^3 + ... + r^{n-1} - nr^{n}$
となり、右辺に初項1公比rの等比数列の和の式が出てくる。
上の数列は等差部分を削除したが今回は公差を1にするための変形を行う。
ここで
$S_1 = 1\times A_1 + 2\times A_2 + ... + M\times A_M$
$S_2 = \qquad 1\times A_2 + 2\times A_3 + ... + M\times A_{M+1}$
$ \qquad \qquad .$
$ \qquad \qquad .$
$ \qquad \qquad .$
のように試しにおいてみる。
$S_1 - S_2 = A_1 + A_2 + A_3 + ... - M \times A_{M+1}$ から
$S_2 = S_1 - (A_1 + A_2 + A_3 + ...+A_M) + M\times A_M+1 - ①$
となる。ここで$1 \leq i \leq M$ の累積和が登場した。
ここで$S_i$と同様に
$T_1 = A_1 + A_2 + A_3 + ...+A_M$
$T_2 = A_2 + A_3 + ...+ A_M + A_{M+1}$
とおくと
$T_1 - T_2 = A_1 - A_{M+1}$
$T_2 = T_1 - A_1 + A_{M+1}$
①は
$S_2 = S_1 - T_1 + M\times A_{M+1}$
$T_2 = T_1 - A_1 + A_{M+1}$
となり $S_1$ と $T_1$は
$S_1 = \sum_{i=1}^{M} i \times A_i$
$T_1 = \sum_{i=1}^{M} A_i$
と即座に求まる。
よって $1 \leq i \leq N-M$において
$S_{i+1} = S_i - T_i + M\times A_{M+i}$
$T_{i+1} = T_i - A_i + A_{i+1}$
の漸化式の元、順に$S_i, T_i$を求めていき、
$ max \quad S_i$ を求める。そしてこの時の計算量は$O(N)$,TLEとならずに済む。
ソースコード
n,m = map(int, input().split()) #n,m 入力
a = list(map(int, input().split())) #a 入力
ss =0
tt =0
for i in range(0,m,1):
ss += (i+1)*a[i] #s1
tt += a[i] #t1
ans = ss
for i in range(0,n-m,1):
ns = ss - tt + m * a[m+i] #si+1 = si - ti + m * a[m+i]
nt = tt - a[i] + a[i+m] #ti+1 = ti - a[i] + a[i+m]
ans = max(ans,ns)
#最大値を更新
tt = nt
ss = ns
print(ans)
実行時間は181ms,Pythonでも余裕ですね。
2. 267-D問題
問題
長さ $N$ の整数列 $A = (A_1,A_2,...,A_N)$ が与えられる。
長さ$M$ の$A$ の連続部分列(連続でなくてもよい)$B = (B_1,B_2,...,B_M)$ に対する $\sum_{i=1}^{M} iB_i$ の最大値を求めよ。
制約
$1\leq M\leq N\leq 2000 $
$-2 \times 10^5 \leq A_i \leq 2 \times 10^5 $
解法
単純に解くことを考えるととてもではないが、先ほどと同じようにはいかない。
こんな時に有効なアルゴリズムがある。それは動的計画法。
動的計画法を知らない人のために簡単に説明する。一番有名な問題に0-1ナップサック問題というのがある。ナップサックには重さの限度(容量)、各荷物に重さと価値が決められていて、容量をオーバーしない範囲でナップサック内の荷物の価値の合計を最大化するという問題である。一般的にdpテーブルを作成し、漸化式を解くことで各$(i,j)$における最大値を更新していくという仕組みだ。また今度詳しく説明する予定。
この人の説明が分かりやすかったのでよかったらどうぞ。
Qitta
$dp[i][j]$とは荷物$i$までを考査に入れた中で、容量$j$のときの価値の合計の最大値を示していることになる。
これを本問に適用すると
$dp[i][j]$は$A_i$までのうちすでに$j$個選んだ時の$\sum_{k=1}^{j} k \times B_k$
の最大値ということになる。
Atcoderのサンプル1でdpテーブルを作成すると以下のようになる。
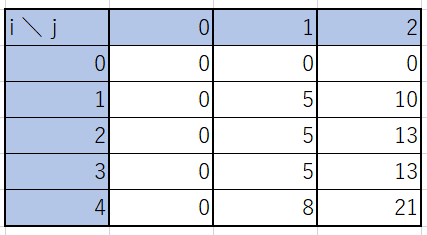
また各$A_i$は
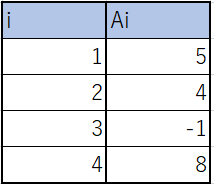
のようになっている。
動的計画法の更新式を定式化すると
$dp[i][j] = max(dp[i-1][j], dp[i-1][j-1] + j \times A_i)$
となる。
左辺右側は部分列として$A_i$を採用しないとき、右辺右側は$A_i$を採用するときの更新である。
ソースコード
N,M=map(int,input().split())
A=[0]+list(map(int,input().split())) #一つインデックス番号をずらす
DP=[[-10**15]*(M+1) for _ in range(N+1)] #ものすごく小さい数が好ましい
DP[0][0]=0
for i in range(1,N+1):
for j in range(M+1):
if j==0: #j =0 のときは左上のマスがないため
DP[i][j]=0
else:
DP[i][j]=max(DP[i-1][j],DP[i-1][j-1]+j*A[i])
print(DP[N][M])
計算量は$O(NM)$となり、十分間に合う。
以上。