動的計画法とは
動的計画法(Dynamic Programming、通称DP)とは、その時々の計算結果を表の形式で保持しておくことによって計算を楽にするアルゴリズムです。
文章で書いても(少なくとも私は)分からないので、実際にPythonで問題を解いてみましょう。
使用例
1.フィボナッチ数列
フィボナッチ数列のn番目の数が何かを求めるプログラムを動的計画法で書いてみます。
コード
def fibonacci(n):
# 最初は[1, 1]
fib_list = [1] * (n + 1)
# 3番目以降
for i in range(2, n + 1):
fib_list[i] = fib_list[i - 1] + fib_list[i - 2]
return fib_list[n - 1]
解説
-
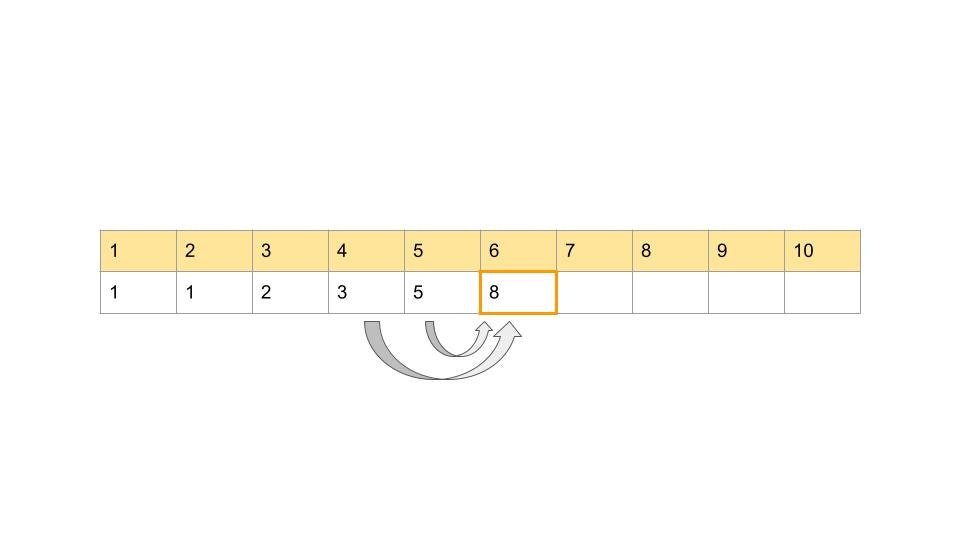
fib_listに[1, 1]をセットする - 3番目以降は、
fib_listの一つ前と二つ前の数字から算出する
この方法だと、n+1回でn番目の数を算出できるので、計算量は**O(n)**になります。
ちなみに、再帰法で同様のアルゴリズムを書くと下記のようになります。
この場合、計算量は指数関数的に増加していくので、いかにDPの計算量が少ないかがわかります。
def fibonacci(n):
if n == 1 or n == 2:
return 1
return fibonacci(n - 1) + fibonacci(n - 2)
2.部分和問題
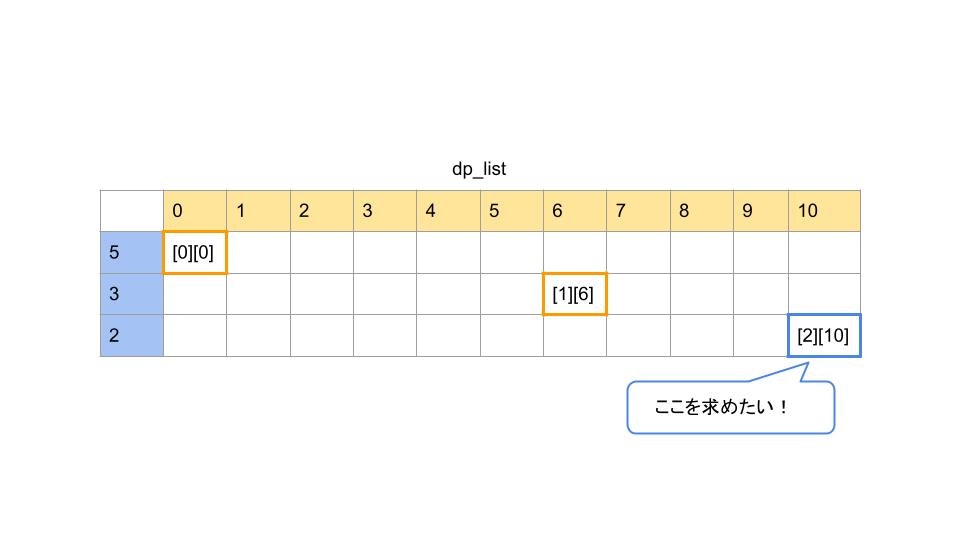
それぞれ5円、3円、2円の駄菓子が売ってあります。お小遣いを10円持っている時、最大何円分の駄菓子が買えるかを求めるプログラムを書いてみます。(ただし、同じ種類の駄菓子はひとつまでしか買えないとします。)
コード
def max_sum(num_list, limit):
num_list_len = len(num_list)
dp_list = [[0 for _ in range(limit + 1)] for _ in range(num_list_len)]
# 1番目の商品
for i in range(limit + 1):
if i >= num_list[0]:
dp_list[0][i] = num_list[0]
# 2番目以降の商品
for i in range(num_list_len):
for j in range(limit + 1):
no_choice = dp_list[i - 1][j]
# 商品の値段より限度額が小さい時
if j < num_list[i]:
dp_list[i][j] = no_choice
# 商品の値段より限度額が大きい時
else:
choice = dp_list[i - 1][j - num_list[i]] + num_list[i]
# 商品を買った時と買わない時で、より大きい金額になる方を選択
dp_list[i][j] = max(choice, no_choice)
return dp_list[num_list_len - 1][limit]
num_list = [5, 3, 2]
limit = 10
print(max_sum(num_list, limit))
解説
- 駄菓子の値段のリスト(
num_list)と、お小遣いの額(limit)をセットする - 1種類目の駄菓子を買えるか買えないかを判断し、合計金額を表(
dp_list)に入力する - 2種類目以降の駄菓子を買うか買わないかを判断し、合計金額を表に入力する
- すべての入力が終わった後、お小遣い以下で一番大きい合計金額を出力する
まず、1種類目の駄菓子を買えるかどうかですが、今回の場合、お小遣いを4円以下しか持っていなければ1種類目の駄菓子(5円)を買うことはできないので、表に「0」を入力します。
逆に、お小遣いを5円以上持っていれば駄菓子を買うことができるので、表に「5」を入力します。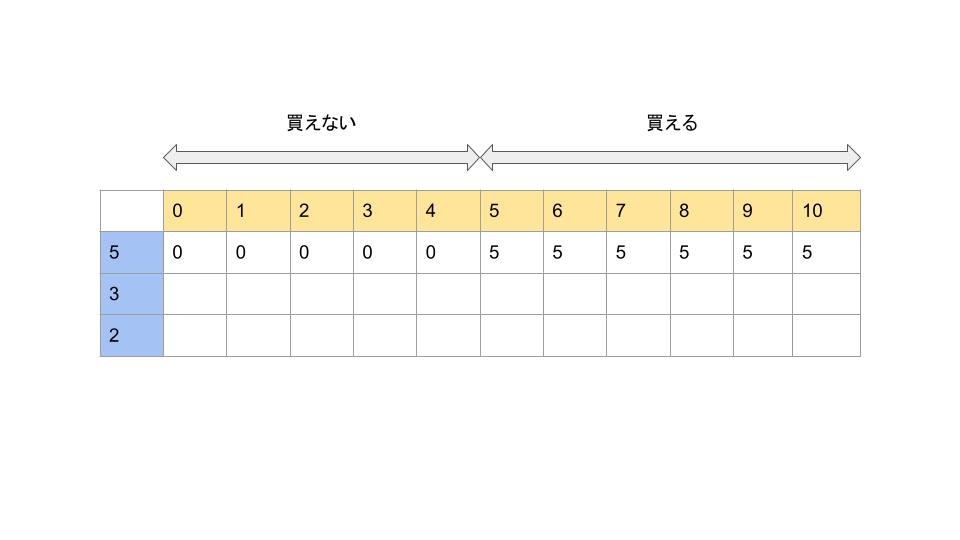
次に、2種類目以降の駄菓子を買うかどうかですが、これを決めるには二つの金額を比較する必要があります。
「駄菓子を買った場合の合計金額」と「駄菓子を買わなかった場合の合計金額」です。
「買わなかった場合」の合計金額は簡単です。表の一つ上の段の自分の列の金額をそのまま持ってくれば良いです。
お小遣いの金額より駄菓子の値段の方が大きい場合は買うことができないので、問答無用で「買わなかった場合」の金額を入力します。
「買った場合」の計算は少し頭を使います。
駄菓子を買うには、その駄菓子の金額分のお小遣いが残っていないといけません。
なので、表の一つ上の段の、その駄菓子の金額分戻った列の金額に、その駄菓子の金額を足したものが「駄菓子を買った場合」の合計金額になります。
「買った場合」と「買わなかった場合」それぞれの金額が求められたら、より大きい方の金額が**「お小遣いの中で買える駄菓子の合計金額の最大値」**になります。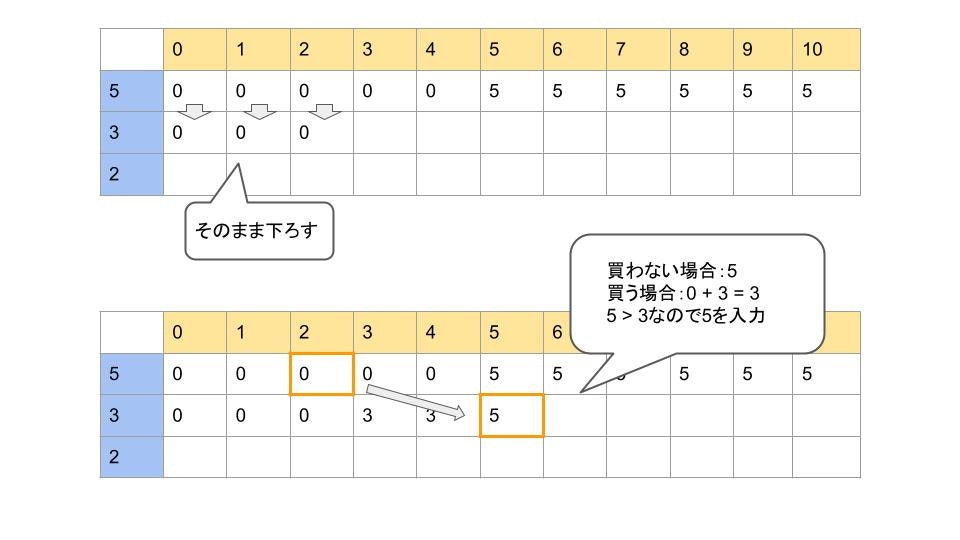
表を埋め終わったら、持っているお小遣いにおける最大合計金額を出力します。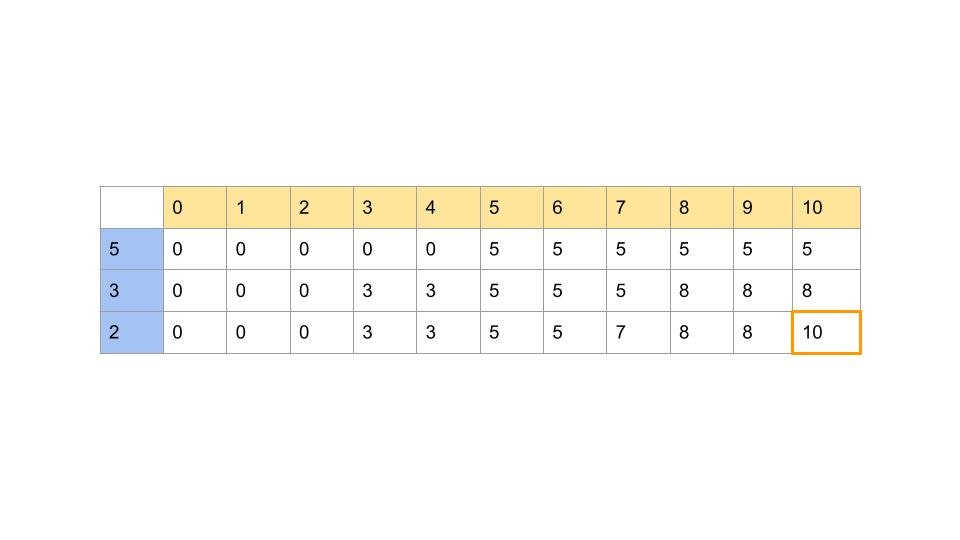
このアルゴリズムの計算量は、表を埋めるのに必要な計算の数なので
縦n(駄菓子の種類)×横m(0~お小遣いの金額)
つまり、**O(nm)**と表すことができます。
他のアルゴリズムに関する記事
筆者より
アルゴリズム初心者なので、間違っている点や説明不足な点は教えていただけるとありがたいです!
例題や別のアルゴリズムなど、随時更新していこうと思います。