【統計学・データ分析】確率の基礎

##はじめに
皆さん、こんにちは。@Raphael_de_murlです。前回の集合に続きに今回は確率について共有していきたいと思います。少し分けて【確率の基礎、離散型確率、連続型確率】の順に紹介します。今回はその1番目で確率の基礎だけ軽く紹介します。

##確率

偶然起こる現象の、現象全てに対する割合の事である。起こりやすさを数値で表した指標として使われる。

####1)数学的確率
数学的確率P(A)：「有限な全事象Uの部分集合である事象Aの起こる確率」と定義しています。ここで全事象が何かを見てみましょう。
【統計学・データ分析】集合の基礎ここの記事で試行や事象などを扱いました。
少し繰り返すと「サイコロを振ったり」、「コインを投げたり」など繰り返すことが可能な行為を施行と言いました。
またその結果「表が出たり」、「3以上の目が出たり」することを事象と言いました。そして基本的な1つ1つの事象を根元事象と呼び、
対象になる全ての根元事象(要素)から成る集合を全事象や事象の全体と呼びます。
P(A)を求める公式は以下のようです。

【3分でわかる！】確率の問題を解くための6つの基礎知識

####練習問題

####2)反復試行の確率
まず独立な試行について見てみます。
これは独立な試行T1,T2があり、T1における事象A、T2における事象Bを考えるとき、試行T1でAが起こり、かつ試行T2でBが起こる確率は、P(A) x P(B)となります。例を入れて説明するとサイコロを1回目に振って3以下の目が出ることと、2回目に振って、5の目が出ることとは、無関係であり、このように2つの結果がお互いに全く影響を与えないときの試行を言います。話を戻してこの試行をn回繰り返したとき、事象AがK回起こる確率を反復試行の確率といいます。確率を求める公式は以下のようです。

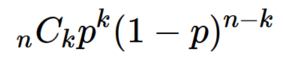
• p：1回の試行で、事象Aの起こる確率
• 1-p(q)：事象Aの起こらない確率

この試行をn回行って、そのうちk回だけ事象Aの起こる確率を計算します。

####練習問題

####3)条件付きの確率
条件付き確率：ある事象が起こっている条件を下で、別の事象が起こる確率。これをある事象A、Bを例として見ると分かりやすいと思います。

これをまた【確率の乗法定理】を使ってこう表せます。
分子のP(A∩B)をP(A)・P(B|A)に表示し、P(B)・P(A|B)にも表示します。

####事後確率
上記に紹介した条件付きの確率の公式を少し変化したものがあり、それを事後確率と呼びます。これはベイズの定理で表せる確率でもあります。実際どう変形されたのかを見てみましょう。

###参考
スバラシク実力がつくと評判の統計学キャンパス・ゼミ―大学の数学がこんなに分かる!単位なんて楽に取れる!
確率
反復試行の確率の公式といろいろな例題
反復試行の確率とは？1からはじめる場合の数
ベイズの定理の基本的な解説