【統計学・データ分析】集合の基礎

##はじめに
皆さん、こんにちは。@Raphael_de_murlです。今年も残りわずかですよね。今回の記事が2018年の最後の投稿になると思います。今回のテーマはタイトルの通り少し数学的な話になります。もちろん！説明は理解やすくしますのでご安心してください！いざ！出発です。

##概要
数学の何の話かと言うとまずは集合からです。中学生ぐらいからずっと学んでいて未だにもプログラミングでよく使われる数式ですよね。特にAIや機械学習の分野ではアルゴリズムが大事なので数学の知識は必須だと思います。（微積分までは知らなきゃいけないですよね…）

##集合とは
高等学校数学A/集合と論理今回はこちらのサイトを参考にしました。

ある事柄の集まりのうち、定義が具体的に示されている物を集合（しゅうごう、英：set）という。例えば、「自然数」は「n > 0となる整数n の全体」という定義があるので、集合といえるが、「大きな数」は、どこからが大きな数といえるのかがはっきりしないため、集合とはいえない。ただし、「大きな数」を例えば「1億以上の整数」と定義すれば集合になりえる。

集合は、一般的にはA、B、X、Yなどのアルファベットの大文字で表し、集合を構成しているものを要素または元と呼びます。そして、aが集合Aの要素であるとき、a∈Aと表し、bが集合Aの要素ではないときは、b∉Aと表します。

簡単な例をみてみましょう。

sample.py

"集合A：５で割り切れる３０以下の自然数"
A = {n|n=5k (k=1,2,3,4,5,6)}
A = {5,10,15,20,25,30}
A = {}

上記のように2通りの表し方があります。要素の個数が有限の集合を有限集合と呼び、A={n|n=5k}のように、要素の個数が無限の集合を無限集合と呼びます。そして一番下のように1つの要素も持っていない集合を特に空集合と呼び、Φで表します。

##集合の種類
####1）部分集合

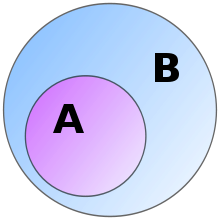
例として、有限集合A、Bを用意します。集合Aの要素が全て集合Bに属するとき、「AはBに含まれる」といい、A⊆BまたはA⊂Bと表し、AをBの部分集合と言います。特にA⊂Bのとき、AはBの真部分集合と言います。部分集合と真部分集合の違いはAがBの部分集合ではあるが、等しくはないであります。

subset.py

A = {"峯岸", "高橋"}
B = {"山本", "峯岸", "高橋", "大島", "岡田"}
A ⊂ B = {"山本", "峯岸", "高橋", "大島", "岡田"}

####2）積集合（共通集合）

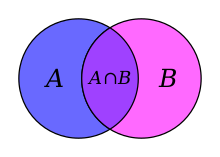
2つの集合A、Bについて共通部分A∩B（AとBに共通な要素全体の集合）と言います。

intersection.py

A = {"渡辺", "山本", "峯岸", "高橋", "横山"}
B = {"山本", "峯岸", "高橋", "大島", "岡田"}
A ∩ B = {"山本", "峯岸", "高橋"}

####3）和集合

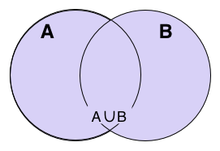
2つの集合A、Bについて和集合A∪B（AまたはBのいずれかに属する要素全体の集合）と言います。

union.py

A = {"渡辺", "山本", "峯岸", "高橋", "横山"}
B = {"山本", "峯岸", "高橋", "大島", "岡田"}
A ∩ B = {"渡辺", "山本", "峯岸", "高橋", "横山" "大島", "岡田"}

####※）A∩BとA∪Bの要素の個数について
共通部分、和集合の要素の個数がΦの場合は次の公式が成り立ちます。

fai.py

A∩B = Φのとき、n(A∪B) = n(A) + n(B)
A∪B = Φのとき、n（A∪B） = n(A) + n(B) - n(A∩B)
※n()は集合の要素の個数を表す。

####4）全体集合

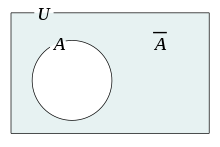
ある集合Aの全てを要素とする集合Uと言います。上に示すように部分集合Aが与えられたとき、補集合は次のように定義します。全体集合Uに属するが、Aには属さない要素から成る集合

####※）UとAと補集合の要素の個数について

##事象
集合は場合の数でよく使われたりします。「コインを投げたり」、「サイコロを振ったり」、同様のことを繰り返すことが可能な行為を試行といい、その結果、「表がでたり」、「偶数の目がでたり」するこれを事象と言います。実際このコインとサイコロを集合で表すと次のようになります。

sample.py

i)コイン：U={表、裏}
ii)サイコロ:U={1,2,3,4,5,6}

このように、試行によって起きる事象は、全て集合によって表すことができるので、集合Aの要素の個数n(A)も、事象Aの場合の数n(A)と呼ぶことにします。
ここで注意することがありまして場合の数と集合では呼び方が異なるので、それを覚えておくとより良いと思います。

集合	場合の数	集合
A∩B	積事象	共通部分
A∪B	和事象	和集合
補集合A	余事象	補集合
φ	空事象	空集合

##まとめに
今回の記事は集合につて学んでみました。これだけたと機械学習やデータ分析系には使われないかと思われるんですが、これを元で関数を作って微積分をやりながらデータを解析することになります。もう強い頭痛が来る感じです。次回は確率に入ります。

##修正
2019年9月29日 - 集合の説明の追加