はじめに
STM32マイコンで「Lチカ」や「UART通信」をするのはもう飽きた……。
そんなある日、X (旧Twitter) のタイムラインで 「オシロスコープに絵を描画している動画」 が流れてきました。緑色の蛍光線で描かれた幾何学模様がグリグリ動く、あのレトロフューチャーな見た目。「かっこいい……自分もこれを手元で再現したい!」と強く感化されました。
幸い、手元には STM32G474RE という、アナログ機能(DAC/OpAmp/Comparator)が異常に強化された「Mixed-Signal MCU」があります。
「この高性能なアナログ機能をフル活用すれば、もっと滑らかに描けるのでは?」
そこで今回は、オシロスコープをディスプレイ代わりにする 「ベクタースキャン(Vector Scan)」 表示に挑戦します。
マイコンのDACからX軸・Y軸の電圧を高速出力して電子ビームを操り、オシロスコープの管面に幾何学模様を描画してみました。
成果物
まずは結果をご覧ください。10種類以上の図形が次々と切り替わる、電子スライドショーの完成です。
なぜSTM32G474なのか?(技術的選定理由)
単にDACがついているマイコンなら他にもありますが、ベクタースキャン描画においてSTM32G474REは以下の2点で圧倒的に有利です。
1. 強力なDAC出力バッファ(Output Buffer)
DACの出力には内部抵抗が存在します。これがオシロスコープの入力容量やケーブルの浮遊容量(C成分)と結合するとローパスフィルタ(RC回路)が形成され、電圧を高速で変化させた際に波形がなまってしまいます。
STM32G4のDACには内蔵オペアンプによる出力バッファが搭載されており、これを Enable にすることで低インピーダンスで信号をドライブできます。これにより、高速描画時でもエッジの効いた「キレのある図形」を描くことが可能です。
2. Cortex-M4FのFPU(浮動小数点演算ユニット)の実力
今回、座標計算や補間処理には float 型を多用します。
通常、FPUを持たないマイコン(Cortex-M0+など)で浮動小数点演算を行うと、コンパイラはソフトウェアライブラリをリンクし、数十〜百サイクルかけてエミュレーション実行します。これでは描画のリアルタイム性は損なわれます。
しかし、STM32G4が搭載する Cortex-M4F コアは、シングル精度のFPU(Floating Point Unit)をハードウェアで内蔵しています。これにより、劇的なパフォーマンス向上が得られます。
① 命令レベルでの圧倒的な差
FPU有効時、浮動小数点の加算や乗算は vadd.f32 や vmul.f32 といった専用のハードウェア命令にコンパイルされ、わずか1〜3サイクル で完了します。
170MHzという高速なクロックに加え、サイクル数自体が1/10〜1/50に短縮されるため、座標変換のような行列演算も「一瞬」で終わります。
② 実装時の注意点: 「f」を忘れるな!
ここで一つ、重要なテクニックがあります。STM32G4のFPUは 「単精度(float)」専用 です。
C言語の仕様上、単に 3.14 と書くと 倍精度(double) として扱われてしまいます。
// 悪い例(激遅)
// xも0.8もdoubleに格上げされ、FPUが使われずソフトウェア処理になる
float x = val * 0.8;
// 良い例(爆速)
// 全てfloatとして扱われ、FPU命令(vmul.f32)が走る
float x = val * 0.8f;
今回のコードで 0.8f や 2047.5f のように、執拗に f サフィックスをつけているのはこのためです。この些細な違いが、オシロスコープ上の描画レートに直結します。
実装の原理と数式モデル
座標系からDAC電圧へのマッピング
図形データは扱いやすいように正規化座標系($-1.0 \le x, y \le +1.0$)で定義します。一方、STM32G4のDACは12bit分解能であり、出力値は $0$ ~ $4095$ の整数値です。
正規化座標 $P_{norm}$ を DACのデジタル値 $D_{dac}$ に変換する式は以下のようになります。
$$D_{dac} = \left( \frac{P_{norm} \times S + 1.0}{2} \right) \times (2^{12} - 1)$$
ここで、$S$ はスケーリング係数(今回は画面端でのクリッピングを防ぐため$0.8$ )です。
この式を展開すると、プログラムに実装する定数が見えてきます。
$$D_{dac} \approx (P_{norm} \times 0.8 + 1.0) \times 2047.5$$
これにより、計算上の原点 $(0,0)$ は DACの中間値である $2047$ (約1.65V) にマップされ、オシロスコープの中心に表示される仕組みです。。
ベクトルによる線形補間(Lerp)
単に頂点の電圧だけを出力すると、オシロスコープ上では「点」しか表示されません。綺麗な「線」として表示させるため、点 から点 へ移動する間を埋める線形補間(Linear Interpolation) を行います。
点 $A(x_1, y_1)$ から点 $B(x_2, y_2)$ への直線のベクトル方程式は、パラメータ $t$ ($0 \le t \le 1$) を用いて以下のように表せます。
$$\vec{P}(t) = \vec{A} + t(\vec{B} - \vec{A})$$
これを離散的なステップ数 $N$ でループ処理する場合、第 $i$ ステップ目の座標 $(x_i, y_i)$ は次のように導出されます。
$$x_i = x_1 + \frac{i}{N}(x_2 - x_1)$$
プログラム上では、この $\Delta x = \frac{x_2 - x_1}{N}$ を事前に計算することで、ループ内を単純な加算処理にし、CPU負荷を最小限に抑えています。
ハードウェア構成
-
MCU: STM32 Nucleo-64 (NUCLEO-G474RE)
-
表示機: X-Yモード機能付きのオシロスコープ
※今回はPC接続型のデジタルオシロ(OWON VDSシリーズ)を使用しています。
昔ながらのアナログオシロはもちろん、最近のデジタルオシロでもX-Yモードがあれば再現可能です。デジタルオシロ特有の「サンプリングの点」が見える描画も、ドット絵のような味があって面白いです。 -
配線:
| Nucleo Pin | 機能 | オシロスコープ |
|---|---|---|
| PA4 | DAC1_OUT1 | CH1 (X軸) |
| PA5 | DAC1_OUT2 | CH2 (Y軸) |
| GND | Ground | 各CHのGND (必須) |
※ GNDが浮いていると、誘導ノイズにより波形が崩壊します(経験済)。
CubeMXの設定
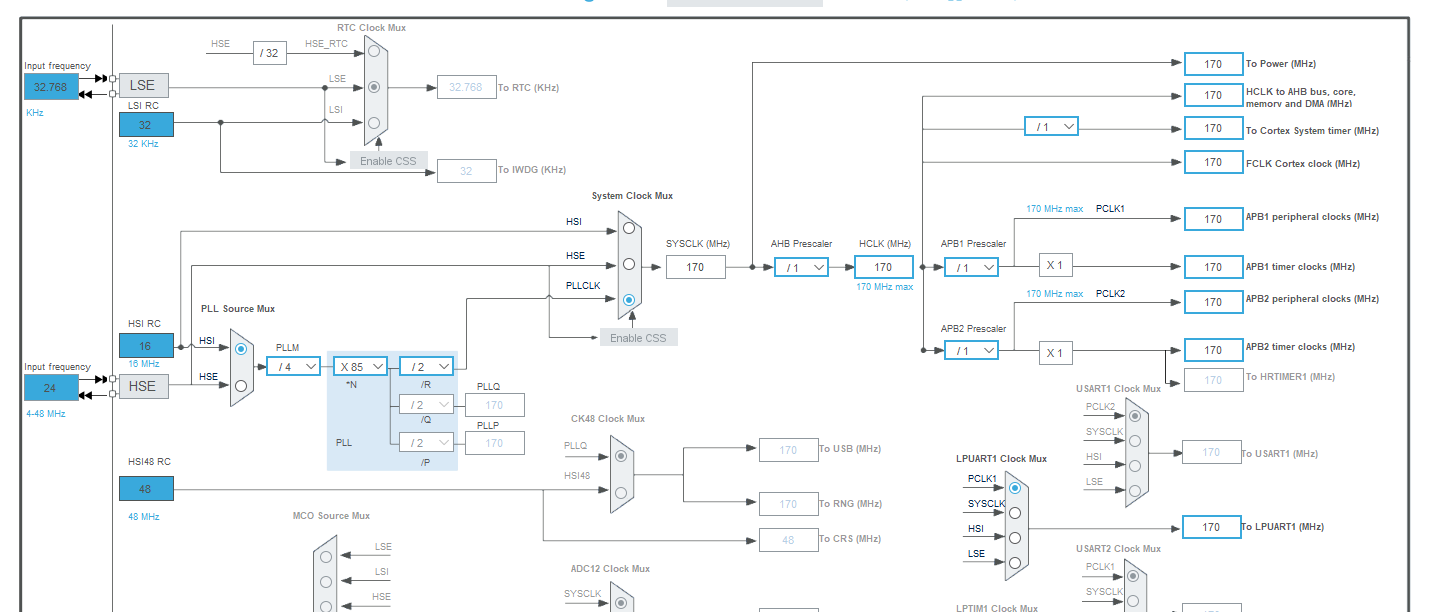
1. Clock Configuration
滑らかな線を描くには処理速度が命です。
HSI (内部高速発振) をソースにして、G474の最大クロックである 170MHz に設定します。
2. Analog (DAC1)
-
OUT1 / OUT2 Mode:
Connected to external pin only - Configuration:
-
Output Buffer:
Enable(前述の通り、ここが重要です)

コードの実装
1. マクロ定義と座標データ
まずは数値扱いのためのマクロと、描画する図形データを定義します。 ここで定義する F2Q31 は、浮動小数点の -1.0 ~ +1.0 を、32bit整数の全範囲(Q1.31形式)にマッピングするものです。
今回は「ハート」「星」「稲妻」などの図形を用意しました。
// 浮動小数点(-1.0 ~ +1.0) を Q1.31固定小数点に変換
// ※ 整数演算での高速化や、CORDICユニットへの入力に使用します
#define F2Q31(x) ((int32_t)((x) * 2147483648.0f))
// 座標構造体
typedef struct { float x; float y; } Point;
// --- 図形データ定義 (一筆書きの順序で) ---
// 1. 四角形 (最後は始点に戻る)
const Point shape_square[] = {
{-0.6f, -0.6f}, { 0.6f, -0.6f}, { 0.6f, 0.6f}, {-0.6f, 0.6f}, {-0.6f, -0.6f}
};
// 2. 三角形
const Point shape_triangle[] = {
{ 0.0f, 0.7f}, { 0.7f, -0.5f}, {-0.7f, -0.5f}, { 0.0f, 0.7f}
};
// 3. 星型 (五芒星)
const Point shape_star[] = {
{ 0.00f, 0.80f}, { 0.47f, -0.64f}, {-0.76f, 0.25f},
{ 0.76f, 0.25f}, {-0.47f, -0.64f}, { 0.00f, 0.80f}
};
// 4. ダイヤ (ひし形)
const Point shape_diamond[] = {
{ 0.0f, 0.8f}, { 0.5f, 0.0f}, { 0.0f, -0.8f}, {-0.5f, 0.0f}, { 0.0f, 0.8f}
};
// 5. 砂時計 (Xのような形)
const Point shape_hourglass[] = {
{-0.5f, 0.7f}, { 0.5f, 0.7f}, {-0.5f, -0.7f}, { 0.5f, -0.7f}, {-0.5f, 0.7f}
};
// 6. 矢印
const Point shape_arrow[] = {
{-0.4f, -0.2f}, { 0.2f, -0.2f}, { 0.2f, -0.6f}, { 0.8f, 0.0f},
{ 0.2f, 0.6f}, { 0.2f, 0.2f}, {-0.4f, 0.2f}, {-0.4f, -0.2f}
};
// 7. 六角形
const Point shape_hexagon[] = {
{ 0.4f, 0.7f}, { 0.8f, 0.0f}, { 0.4f, -0.7f},
{-0.4f, -0.7f}, {-0.8f, 0.0f}, {-0.4f, 0.7f}, { 0.4f, 0.7f}
};
// 8. イナズマ
const Point shape_bolt[] = {
{ 0.3f, 0.8f}, { 0.0f, 0.1f}, { 0.4f, 0.1f}, // 上のギザギザ
{-0.2f, -0.8f}, { 0.1f, -0.1f}, {-0.3f, -0.1f}, // 下のギザギザ
{ 0.3f, 0.8f} // 始点に戻る
};
// 9. 無限大 (∞の字) - 8の字結び
const Point shape_infinity[] = {
{ 0.0f, 0.0f}, {-0.4f, 0.4f}, {-0.8f, 0.0f}, {-0.4f, -0.4f},
{ 0.0f, 0.0f}, { 0.4f, 0.4f}, { 0.8f, 0.0f}, { 0.4f, -0.4f}, { 0.0f, 0.0f}
};
// 10. 渦巻き (四角いスパイラル)
const Point shape_spiral[] = {
{ 0.0f, 0.0f}, { 0.1f, 0.0f}, { 0.1f, 0.1f}, {-0.1f, 0.1f},
{-0.1f, -0.1f}, { 0.2f, -0.1f}, { 0.2f, 0.2f}, {-0.2f, 0.2f},
{-0.2f, -0.2f}, { 0.3f, -0.2f}, { 0.3f, 0.3f}, {-0.3f, 0.3f},
{-0.3f, -0.3f}, { 0.4f, -0.3f}, { 0.4f, 0.4f}, {-0.4f, 0.4f},
{-0.4f, -0.4f}, { 0.5f, -0.4f}, { 0.5f, 0.5f}, {-0.5f, 0.5f},
{-0.5f, -0.5f}, { 0.6f, -0.5f}, { 0.6f, 0.6f}, {-0.6f, 0.6f}
};
// 11. ハート (ローポリゴン風)
// 曲線は難しいので、直線で構成したデジタルなハートです
const Point shape_heart[] = {
{ 0.0f, -0.8f}, // 下の尖った部分
{ 0.7f, -0.1f}, { 0.7f, 0.5f}, { 0.3f, 0.8f}, // 右半分
{ 0.0f, 0.4f}, // 中央の谷
{-0.3f, 0.8f}, {-0.7f, 0.5f}, {-0.7f, -0.1f}, // 左半分
{ 0.0f, -0.8f} // 始点に戻る
};
// --- 図形管理用 ---
typedef struct {
int num_points; // 頂点の数
const Point* points; // 座標配列へのポインタ
} ShapeData;
// 全図形のリスト
const ShapeData my_shapes[] = {
{ sizeof(shape_square)/sizeof(Point), shape_square },
{ sizeof(shape_triangle)/sizeof(Point), shape_triangle },
{ sizeof(shape_star)/sizeof(Point), shape_star },
{ sizeof(shape_diamond)/sizeof(Point), shape_diamond },
{ sizeof(shape_hourglass)/sizeof(Point), shape_hourglass },
{ sizeof(shape_arrow)/sizeof(Point), shape_arrow },
{ sizeof(shape_hexagon)/sizeof(Point), shape_hexagon },
{ sizeof(shape_bolt)/sizeof(Point), shape_bolt },
{ sizeof(shape_infinity)/sizeof(Point), shape_infinity },
{ sizeof(shape_spiral)/sizeof(Point), shape_spiral },
{ sizeof(shape_heart)/sizeof(Point), shape_heart },
};
// ここに丸やバツなどを追加していく
const int NUM_SHAPES = sizeof(my_shapes) / sizeof(ShapeData);
2. 描画ドライバ
数式モデルに基づいたDAC出力関数と、補間関数です。
/* USER CODE BEGIN 0 */
// 座標(-1.0~1.0) を DAC値(0~4095) に変換して出力
void DAC_Out(float x, float y)
{
// マッピング式: D = (P * 0.8 + 1.0) * 2047.5
uint32_t dac_x = (uint32_t)((x * 0.8f + 1.0f) * 2047.5f);
uint32_t dac_y = (uint32_t)((y * 0.8f + 1.0f) * 2047.5f);
// クリッピングガード
if(dac_x > 4095) dac_x = 4095;
if(dac_y > 4095) dac_y = 4095;
HAL_DAC_SetValue(&hdac1, DAC_CHANNEL_1, DAC_ALIGN_12B_R, dac_x);
HAL_DAC_SetValue(&hdac1, DAC_CHANNEL_2, DAC_ALIGN_12B_R, dac_y);
}
// 線分を描画する(線形補間)
void DrawLine(float x1, float y1, float x2, float y2)
{
const int steps = 25; // 分割数(ここを増やすと線が濃くなる)
float dx = (x2 - x1) / steps;
float dy = (y2 - y1) / steps;
for (int i = 0; i <= steps; i++) {
DAC_Out(x1 + dx * i, y1 + dy * i);
}
}
/* USER CODE END 0 */
3. メインループ
2秒ごとに図形を切り替えるスライドショー形式にします。
/* USER CODE BEGIN WHILE */
while (1)
{
// --- 図形の切り替え処理 ---
if (HAL_GetTick() - last_switch_time > 2000)
{
current_shape_idx++;
if(current_shape_idx >= NUM_SHAPES) current_shape_idx = 0;
last_switch_time = HAL_GetTick();
}
// --- 描画処理 ---
const ShapeData* now = &my_shapes[current_shape_idx];
// 一筆書きで全頂点を結ぶ
for(int i = 0; i < now->num_points - 1; i++) {
DrawLine(now->points[i].x, now->points[i].y,
now->points[i+1].x, now->points[i+1].y);
}
}
/* USER CODE END WHILE */
結果
170MHzの処理能力とDACバッファのおかげで、チラつきの全くない、非常にシャープな図形が表示されました。
特にイナズマの鋭角な部分や、図形の交差部分も綺麗に表現できています。デジタル制御ですが、オシロスコープの蛍光表示特有の「滲み」が良いレトロフューチャー感を出しています。
まとめ・今後の展望
STM32G474のDACを使って、理論通りにオシロスコープにお絵かきをすることができました。
「数式通りの波形を、物理的な電圧として出力し、電子ビームを曲げる」というプロセスは、ディスプレイに printf するのとは違った原始的な喜びがあります。
今回は頂点同士を直線で結ぶ「ポリゴン描画」のみでしたが、G474には三角関数を高速計算する CORDIC ユニットも搭載されています。次はこれを使って、3D回転や滑らかな曲線の描画にも挑戦してみたいと思います。