1軸簡易カルマンフィルタで「センサフュージョン」の基礎を固める

3軸リアクションホイール倒立振子を作るアドカレの19日目です。

前回（Day 18）の実装により、高性能6軸IMU（ICM-42688）から加速度および角速度データを取得することに成功しました。しかし、取得した生データ（Raw Data）をグラフ化して詳細に確認したところ、姿勢制御にそのまま使用するには「ノイズ」と「ドリフト」という大きな課題があることが判明しました。

本来、Cubliのような3次元の姿勢制御を行うには、クォータニオン（四元数）を用いた「拡張カルマンフィルタ（EKF）」などの高度なアルゴリズムが必須となります。しかし、センサの特性を把握しないまま複雑な多変量解析の実装を行うと、不具合が生じた際の原因切り分け（センサの問題か、数式の問題か）が困難になります。

そこで今回は、3軸制御へ進む前の重要なステップとして、まずは**「1軸のみのカルマンフィルタ（Kalman Filter）」**を実装します。

あえて1軸に限定することで計算モデルを単純化し、「加速度センサのノイズ」と「ジャイロセンサの積分誤差」をどのように確率統計的に融合（フュージョン）すれば最適な角度が得られるのか、その基本原理と実装効果を確実に検証します。

1. センサデータの特性と課題

倒立振子の姿勢制御において制御入力となる最も重要なパラメータは、 「地面に対する現在の傾斜角（$\theta$）」 です。この $\theta$を算出するために加速度センサとジャイロセンサを使用しますが、それぞれのセンサは物理的な特性上、単独では解決できない弱点を持っています。実測データに基づき、その詳細を解説します。

① 加速度センサの課題：高周波ノイズと並進加速度

加速度センサは、検出した合成加速度ベクトルに対する重力加速度 $g$ の成分比から角度を算出します。制御軸（例えばピッチ角）に関連する $y$ 軸および $z$ 軸の加速度成分をそれぞれ $A_y, A_z$ とすると、角度 $\theta_{acc}$ は以下の式で幾何学的に求められます。

$$\theta_{acc} = \arctan\left(\frac{A_y}{A_z}\right)$$
原理は単純ですが、センサ出力には常に電気的なホワイトノイズが含まれます。さらに深刻なのは、倒立振子自体が動作する際に発生する「並進加速度」や、床面からの「衝撃振動」もすべて加速度として検出してしまう点です。これにより、静止状態であっても出力値は安定しません。

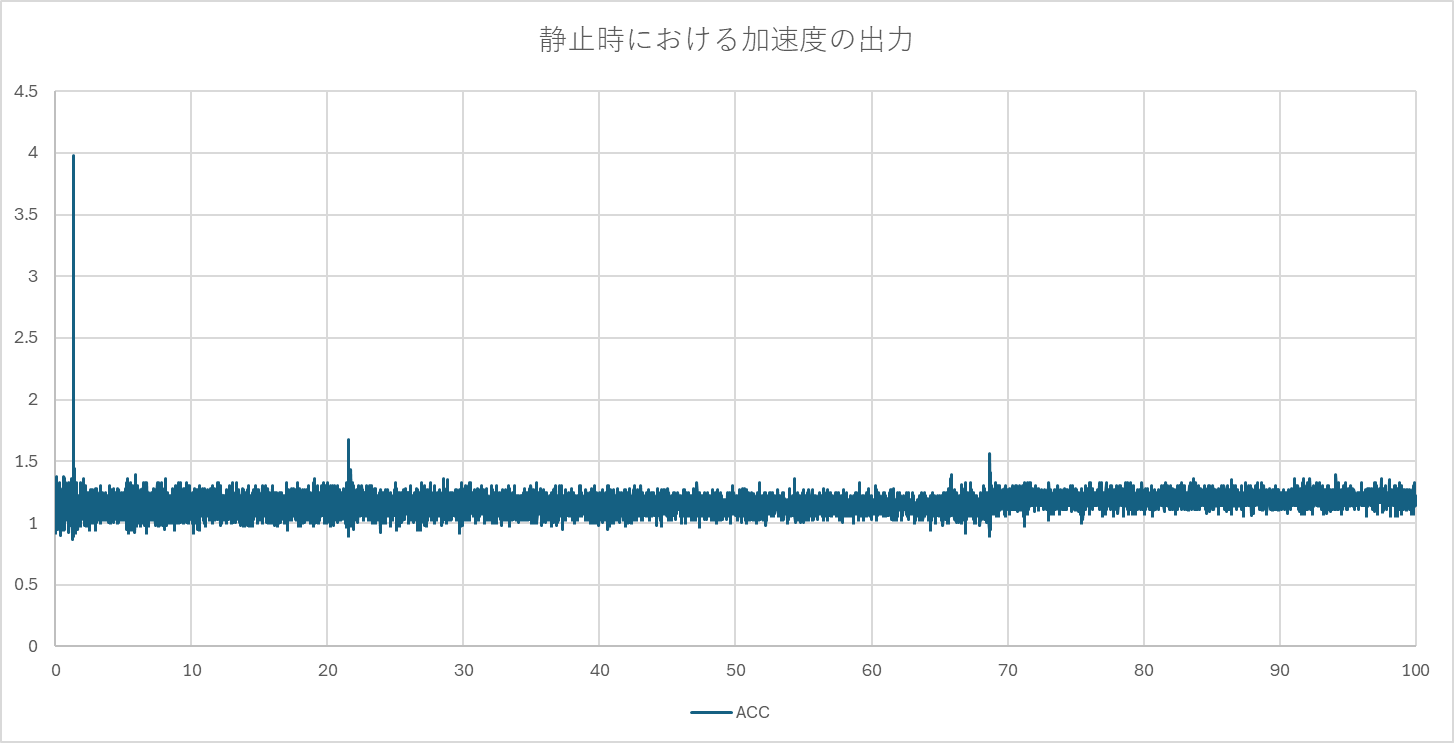
上図の**青線（ACC）**が加速度センサから算出した角度です。常に高周波の振動（ノイズ）が乗っており、この値をそのままPD制御などの入力として使用すると、D操作（微分）によってノイズが増幅され、モータが高周波で振動・発熱し、最悪の場合は制御不能に陥ります。

② ジャイロセンサの課題：低周波ドリフト（積分誤差）

ジャイロセンサは、単位時間あたりの回転角である角速度 $\omega$ [deg/s] を出力します。現在の角度 $\theta_{gyro}$ を得るためには、これを時間積分する必要があります。サンプリング時間を $\Delta t$ とすると、離散時間系では以下の漸化式となります。

$$\theta_{gyro}[k] = \theta_{gyro}[k-1] + \omega[k] \cdot \Delta t$$

ここで問題となるのが 「バイアス（オフセット誤差）」 です。MEMSジャイロセンサは、完全に静止していても出力が厳密に 0 にならず、温度や応力変化に応じた微小な値（例: 0.1 deg/s）が出力され続ける特性があります。積分処理はこの微小な誤差を累積し続けるため、時間は経過するにつれて推定角度が真値から乖離していきます。

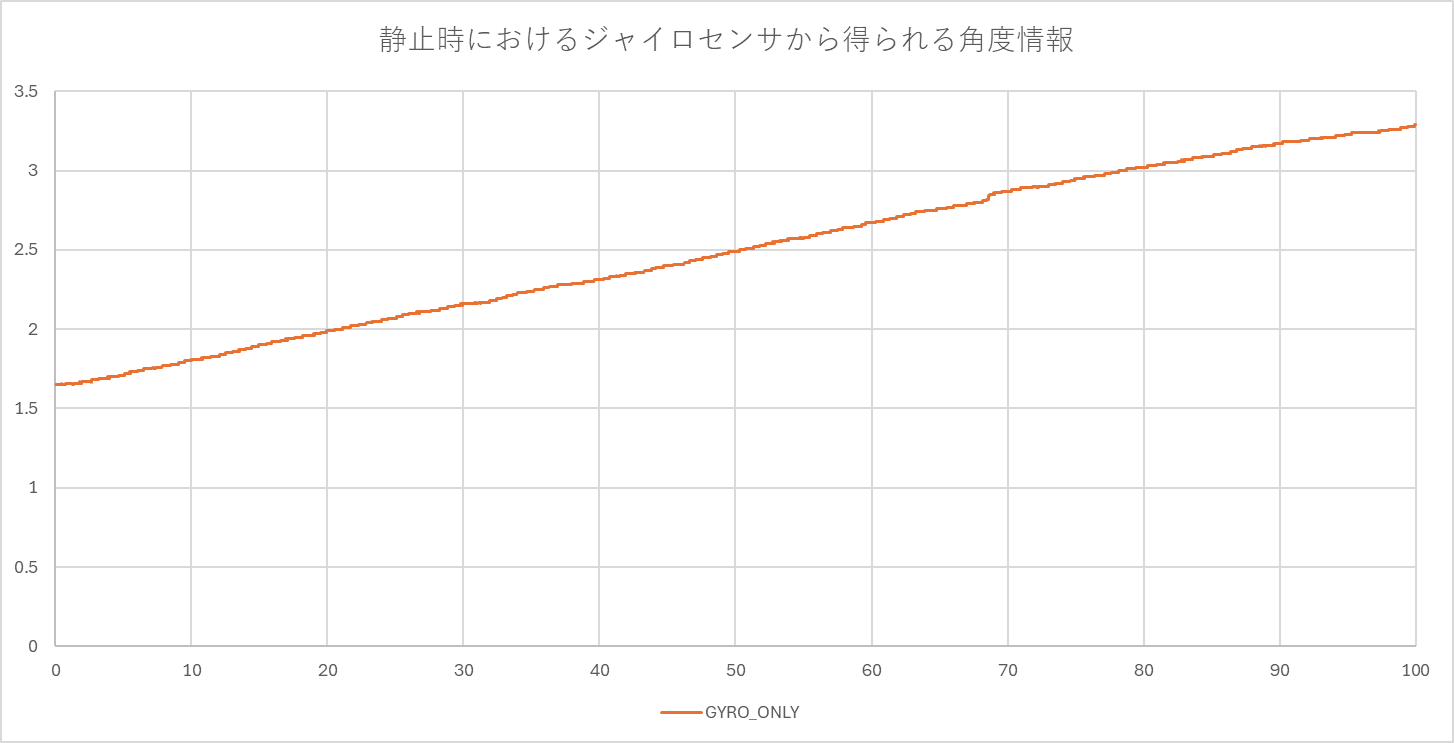
上図の 黄色線（GYRO_ONLY） はジャイロセンサの値を単純積分した結果です。センサは静止しているにもかかわらず、角度が右肩上がりに増加しています。わずか数秒で数度のズレが生じており、この値を制御に用いた場合、システムは「自身が傾いている」と誤認し、それを補正しようとして暴走することになります。

結論：センサフュージョンの必要性

• 加速度センサ： 長期的には重力方向（真値）を指すが、短期的にはノイズが多く信頼性に欠ける。
• ジャイロセンサ： 短期的には滑らかで正確な変化を捉えるが、長期的にはドリフトにより信頼性が低下する。

この両者の特性を相補的に利用し、互いの弱点を打ち消し合うことで最適な角度を推定する手法がセンサフュージョンであり、その代表的なアルゴリズムがカルマンフィルタです。

2. 数理モデル：カルマンフィルタのアルゴリズム

今回はマイコン（STM32）の計算リソースを考慮し、倒立振子の制御軸（1軸）に特化した 「1軸簡易カルマンフィルタ」 を実装します。

システムモデルの定義

カルマンフィルタにおいて推定すべき「状態」を定義します。今回は 「真の角度 $\theta$」 と、ジャイロの誤差要因である 「ジャイロバイアス $\dot{\theta}_{bias}$」 の2つを状態変数とし、状態ベクトル $x_k$ を以下のように定義します。

x_k =
\left[
\begin{array}{c}
\theta \\
\dot{\theta}_{\text{bias}}
\end{array}
\right]

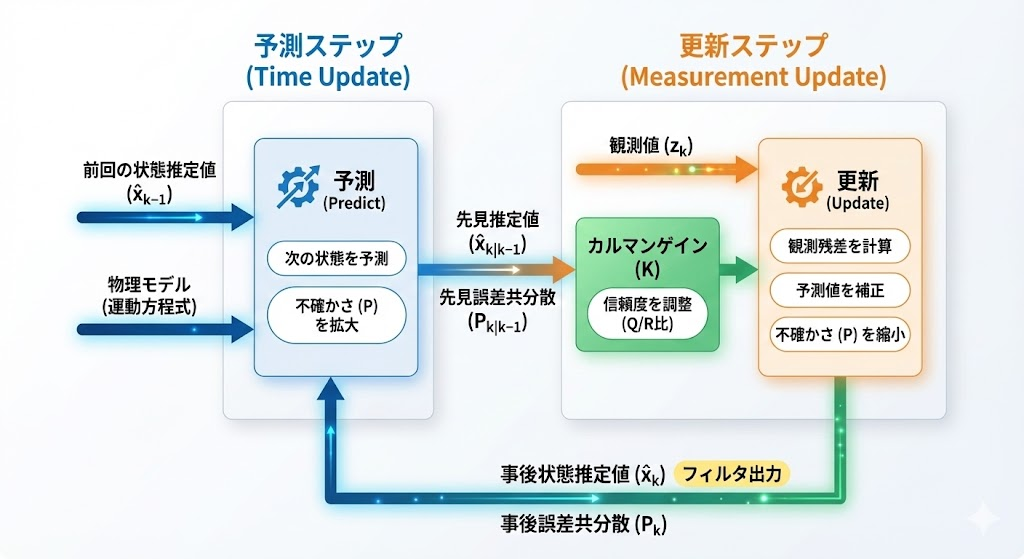
カルマンフィルタは、以下の「予測（Time Update）」と「更新（Measurement Update）」の2ステップを繰り返すことで、真値を逐次推定します。

Step 1: 予測ステップ（Time Update）

現在の状態から、物理モデルに基づいて次の瞬間の状態を予測します。ここでは「角度は角速度によって変化する」という物理法則を用います。ただし、観測された角速度 $\omega_{gyro}$ にはバイアスが含まれていると仮定し、推定されたバイアスを差し引いて計算します。

\begin{aligned} \hat{\theta}_{k|k-1} &= \hat{\theta}_{k-1} + (\omega_{gyro} - \hat{\dot{\theta}}_{bias}) \cdot \Delta t \\ \hat{\dot{\theta}}_{bias, k|k-1} &= \hat{\dot{\theta}}_{bias, k-1} \end{aligned}

同時に、推定値の不確かさを示す誤差共分散行列 $P$ も更新します。ここで $Q$ はプロセスノイズ共分散行列であり、システムのモデル化誤差（予測の不確かさ）を表します。

$$P_{k|k-1} = F P_{k-1} F^T + Q$$

Step 2: 更新ステップ（Measurement Update）

予測された先見推定値に対し、観測値（加速度センサによる角度 $z_{acc}$）を用いて補正を行います。まず、予測値と観測値のズレ（観測残差 $y$）を計算します。

$$y = z_{acc} - \hat{\theta}_{k|k-1}$$
次に、この残差をどれだけ信頼して補正に用いるかを決定するカルマンゲイン $K$ を算出します。ここで $R$ は観測ノイズ共分散であり、加速度センサのノイズの大きさを表します。

\begin{aligned}
S &= H P_{k|k-1} H^T + R \quad (\text{残差共分散}) \\
K &= P_{k|k-1} H^T S^{-1} \quad (\text{カルマンゲイン})
\end{aligned}

最後に、カルマンゲイン $K$ を用いて状態推定値 $x$ と誤差共分散行列 $P$ を更新します。

\begin{aligned}
x_k &= x_{k|k-1} + K \cdot y \\
P_k &= (I - K H) P_{k|k-1} 
\end{aligned}

このアルゴリズムの挙動は、パラメータ $Q$ と $R$ の設定によって決定されます。

• $R$ を大きく設定 $\rightarrow$ 加速度の信頼度を下げる $\rightarrow$ ノイズは減るが、ドリフト補正が遅くなる。
• $R$ を小さく設定 $\rightarrow$ 加速度を信頼する $\rightarrow$ ドリフトは消えるが、ノイズが乗りやすくなる。

3. 実装：C言語によるコード

行列演算ライブラリを使用すると計算負荷が高くなるため、上記の行列演算を手計算で展開し、構造体を用いて実装した軽量なCコードを示します。

#include <math.h>

// カルマンフィルタ構造体
typedef struct {
    float Q_angle;   // 角度推定のプロセスノイズ分散
    float Q_bias;    // ジャイロバイアスのプロセスノイズ分散
    float R_measure; // 加速度センサの観測ノイズ分散
    
    float angle;     // 出力：推定された「真の角度」
    float bias;      // 出力：推定された「ジャイロバイアス」
    float P[2][2];   // 誤差共分散行列
} Kalman_t;

// 初期化関数
void Kalman_Init(Kalman_t *kalman) {
    kalman->Q_angle = 0.001f;
    kalman->Q_bias  = 0.003f;
    kalman->R_measure = 0.03f;
    
    kalman->angle = 0.0f;
    kalman->bias  = 0.0f;
    
    kalman->P[0][0] = 0.0f;
    kalman->P[0][1] = 0.0f;
    kalman->P[1][0] = 0.0f;
    kalman->P[1][1] = 0.0f;
}

// カルマンフィルタ更新関数
// newAngle: 加速度センサから算出した角度 [deg]
// newRate:  ジャイロセンサから取得した角速度 [deg/s]
// dt:       サンプリング周期 [s]
float Kalman_getAngle(Kalman_t *kalman, float newAngle, float newRate, float dt) {
    // --- 1. 予測ステップ (Time Update) ---
    
    // 状態の予測: 前回の角度に、バイアス補正後の角速度成分を加算
    float rate = newRate - kalman->bias;
    kalman->angle += rate * dt;

    // 誤差共分散行列 P の更新
    // F = [1, -dt; 0, 1] として展開
    kalman->P[0][0] += dt * (dt * kalman->P[1][1] - kalman->P[0][1] - kalman->P[1][0] + kalman->Q_angle);
    kalman->P[0][1] -= dt * kalman->P[1][1];
    kalman->P[1][0] -= dt * kalman->P[1][1];
    kalman->P[1][1] += kalman->Q_bias * dt;

    // --- 2. 更新ステップ (Measurement Update) ---
    
    // 観測残差の計算
    float S = kalman->P[0][0] + kalman->R_measure;
    
    // カルマンゲイン K の計算
    float K[2];
    K[0] = kalman->P[0][0] / S;
    K[1] = kalman->P[1][0] / S;

    // 観測値（加速度角度）との差分算出
    float y = newAngle - kalman->angle;

    // 状態推定値の更新
    kalman->angle += K[0] * y;
    kalman->bias  += K[1] * y;

    // 誤差共分散行列 P の事後更新
    float P00_temp = kalman->P[0][0];
    float P01_temp = kalman->P[0][1];

    kalman->P[0][0] -= K[0] * P00_temp;
    kalman->P[0][1] -= K[0] * P01_temp;
    kalman->P[1][0] -= K[1] * P00_temp;
    kalman->P[1][1] -= K[1] * P01_temp;

    return kalman->angle;
}

4. 検証：動的特性の評価

① 動特性の評価：ノイズと遅延の抑制

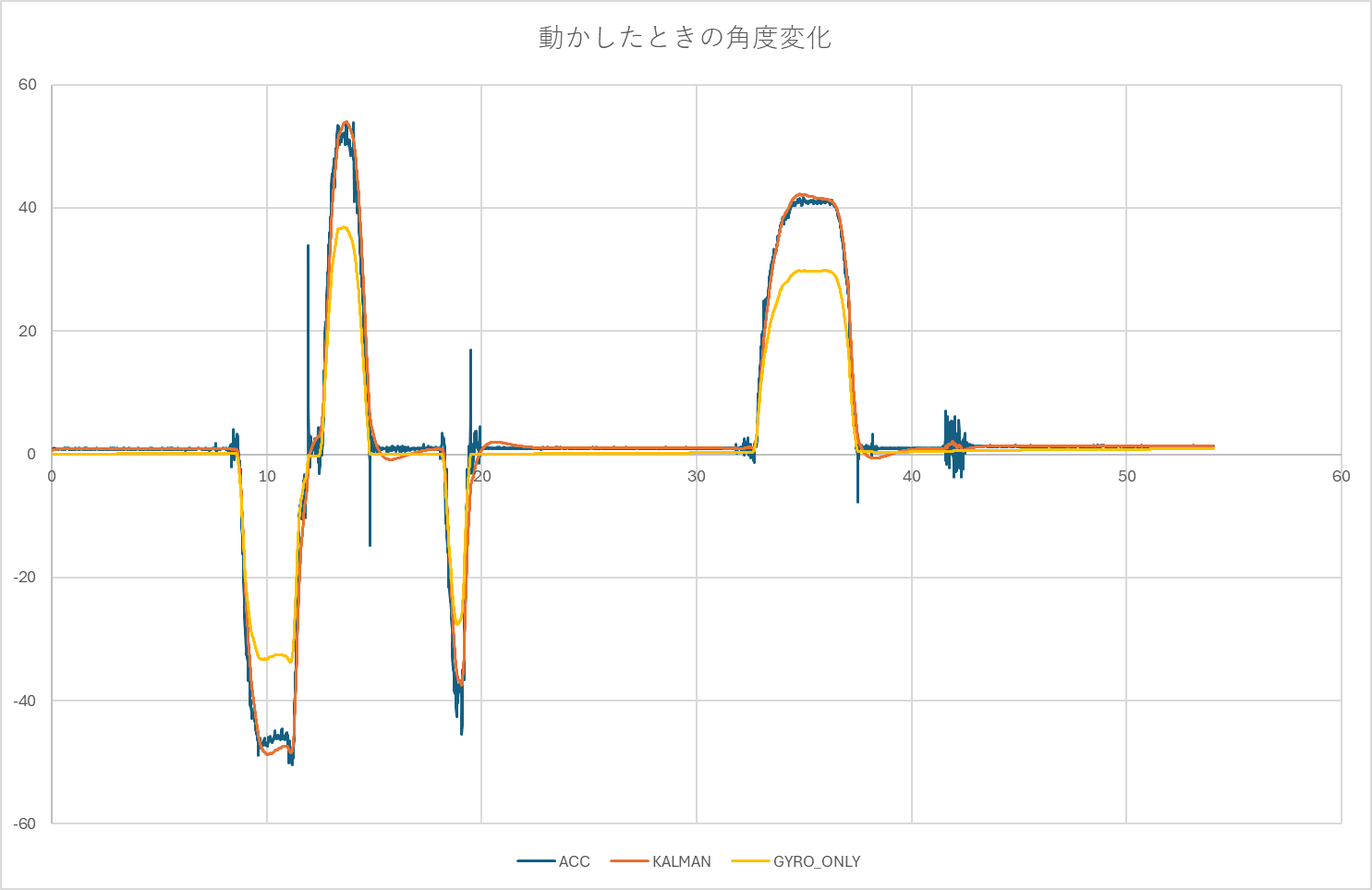
センサを手で持ち、激しく振った際の応答波形を確認します。

このグラフからは、以下の改善効果が確認できます。

• 高周波ノイズの除去： 青線（ACC）に重畳している激しいスパイクノイズが、オレンジ線（KALMAN）では完全に除去されています。
• 位相遅れのなさ： フィルタリングされているにもかかわらず、波形の立ち上がり・立ち下がりのタイミングにおいて、青線（生データ）に対する遅延がほぼゼロです。これは、ジャイロセンサの高応答性を活かせている証拠です。

② 静特性の評価：積分ドリフトの補正

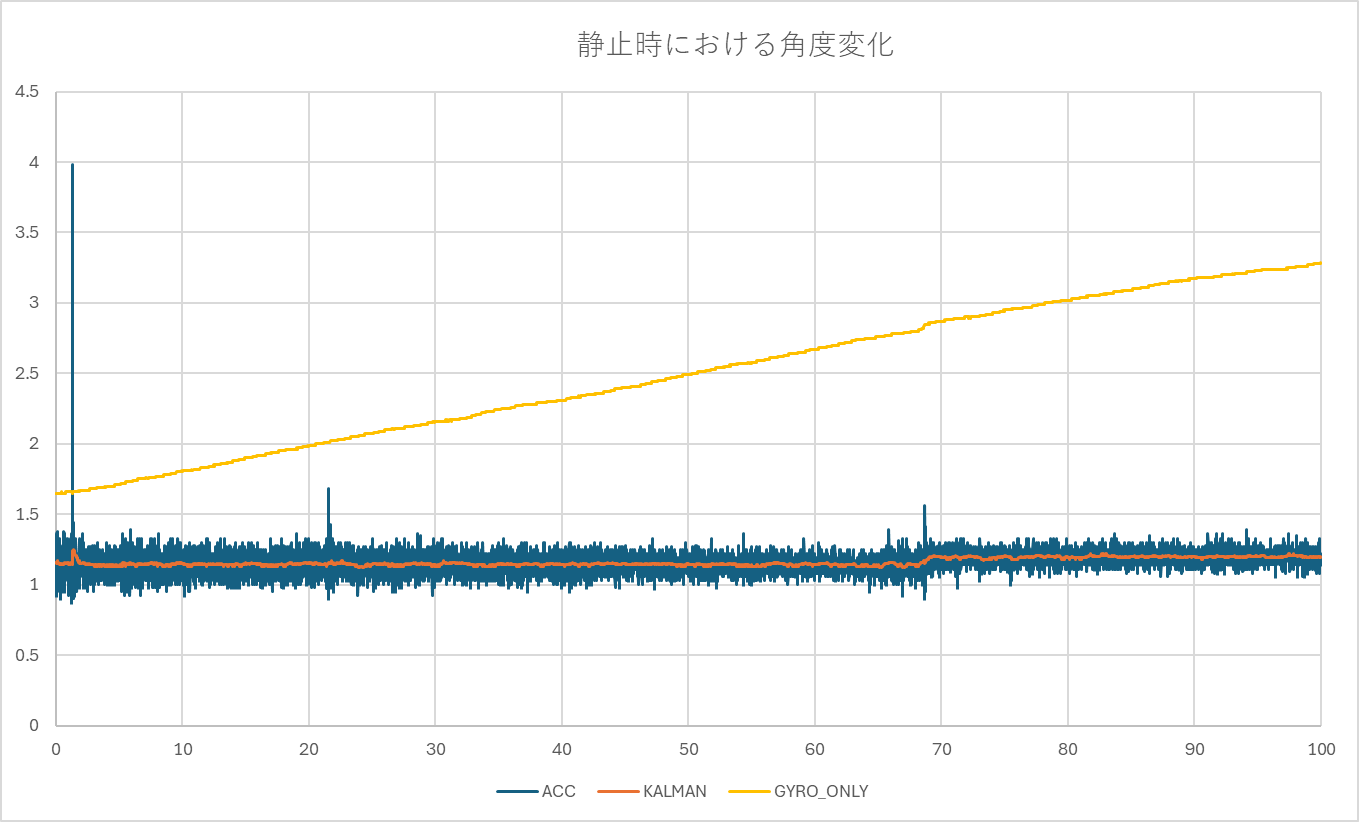
次に、センサを机の上に固定し、静止状態を維持した際の波形を確認します。

このグラフは、カルマンフィルタ（センサフュージョン）の真価を最も端的に表しています。

• ジャイロ単体の積分（黄色線）： 時間経過とともに右肩上がりに数値が増大しています。わずか数秒で $1.5^\circ$ から $3.3^\circ$ へと約 $1.8^\circ$ もドリフトしており、これを制御に用いれば、ロボットは直立しているつもりで加速し続ける（暴走する）ことになります。

• カルマンフィルタ（オレンジ線）： 黄色線がドリフトしていく中でも、常に加速度センサ（青線）の示す重力方向を参照し続けているため、一定値（約 $1.2^\circ$）に収束・安定しています。

結論

実験の結果、今回実装した1軸カルマンフィルタは、「動的な急変にはジャイロのように素早く反応」 し、かつ 「静的には加速度のようにドリフトしない」 という、理想的な角度データを出力することが確認できました。

5. まとめ

今回は、倒立振子制御の要となる「姿勢推定」の第一弾として、カルマンフィルタを実装しました。

• 加速度のノイズ → ジャイロ情報で平滑化して消した。
• ジャイロのドリフト → 加速度情報で補正して消した。

互いの弱点を補い合うことで、「滑らか」かつ「正確」な角度データを手に入れました。

しかし、今回実装したのはあくまで「1軸」の傾きを見るための簡易的なものです。目できである　「3軸倒立振子（Cubli）」　は、3次元空間を複雑に回転するため、これだけでは制御しきれません。

次回（Day 20）は、現代制御理論の深淵、　「拡張カルマンフィルタ（Extended Kalman Filter: EKF）」　の実装に挑みます！
行列演算とクォータニオン（四元数）を駆使し、3軸すべての姿勢を完璧に捉える　「最強のアルゴリズム」　をSTM32に実装しましょう。お楽しみに！