0. はじめに
2020年9月7日にAtCoder公式のアルゴリズム集 AtCoder Library (ACL)が公開されました。
私はACLに収録されているアルゴリズム、データ構造のほとんどが初見だったのでいい機会だと思い、アルゴリズムの勉強からPythonでの実装までを行いました。
この記事ではDSUをみていきます。
対象としている読者
- DSUってなに?という方。
- ACLのコードを見てみたけど何をしているのかわからない方。
- C++はわからないのでPythonで読み進めたい方。
参考にしたもの
AtCoder公式によるわかりやすい解説があります。
- スライド
- youtube解説動画(ABC157の解説動画です)
1. DSUとは
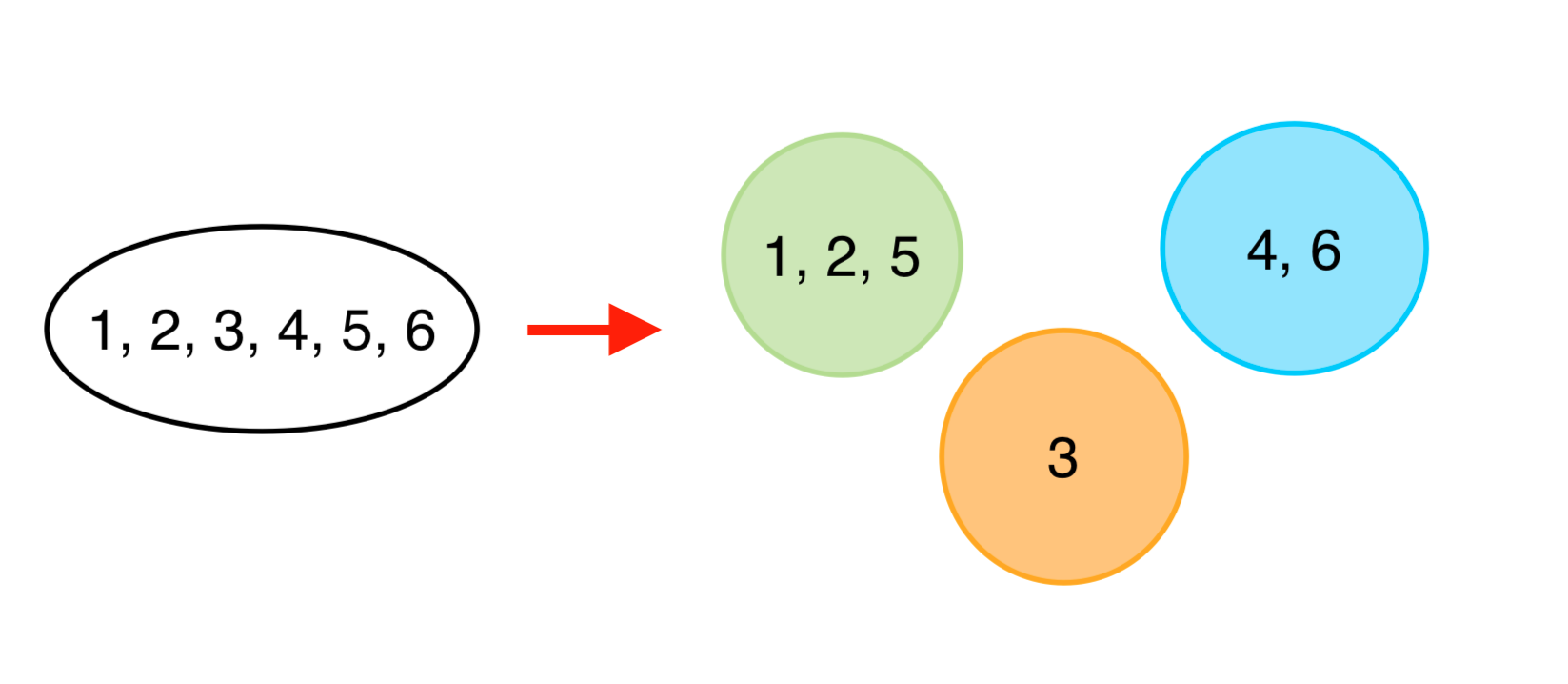
DSU (Disjoint Set Union, 素集合データ構造)はあるデータ集合を素集合(グループ)に分割して保持するデータ構造です。すなわち各データが1つのグループに属し、2つ以上のグループに属することはありません。
このデータ構造は以下の2つの便利な操作をサポートしています。
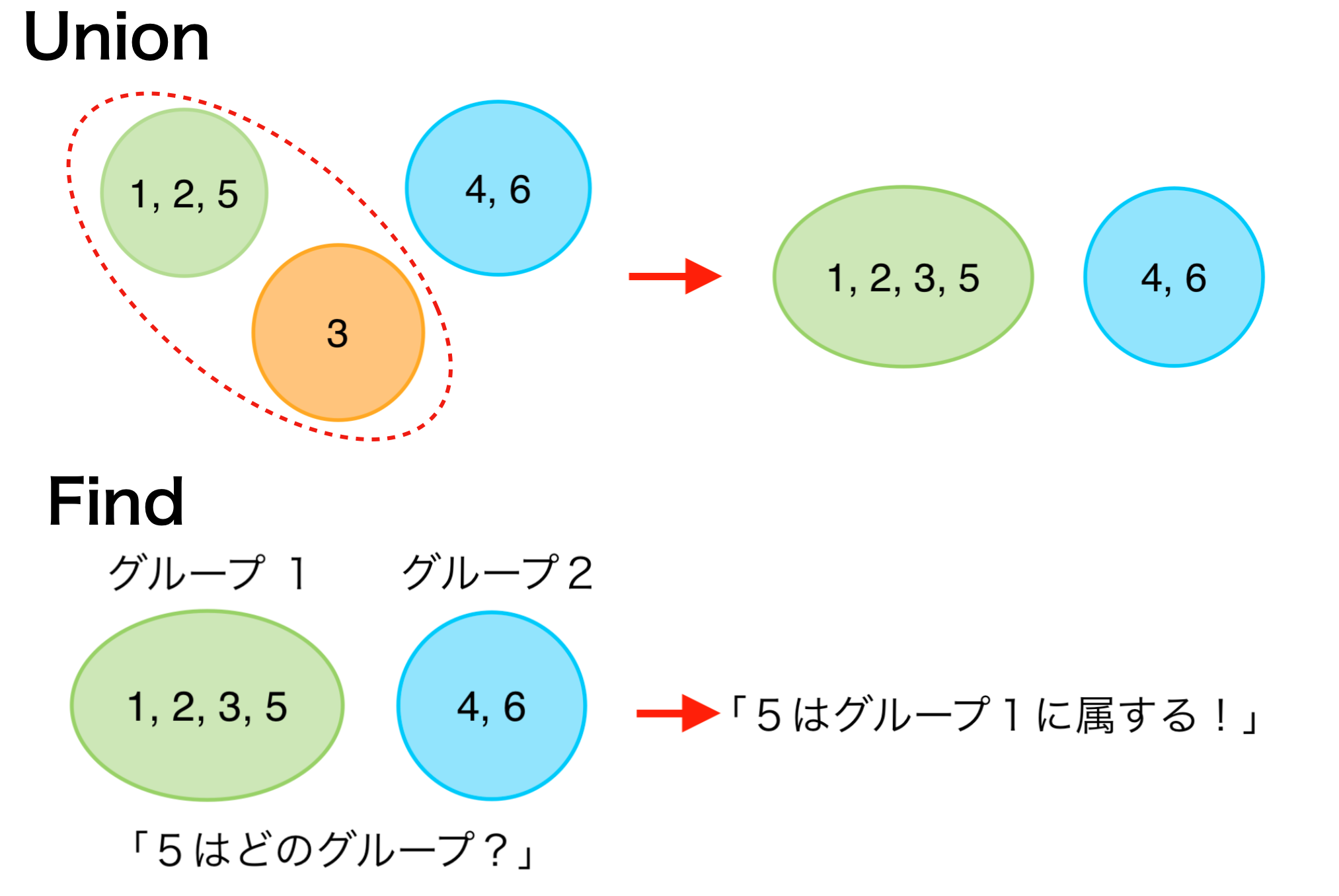
- Union: 2つのグループを1つに統合する。
- Find: ある要素がどのグループに属するかを求める。
このことから、このデータ構造をUnionFindと呼ぶこともあります。こちらの名称の方が馴染みがあるかもしれません。
実装上は...
Unionはグループではなく要素を2つ指定し、それらの属するグループを統合します。また、各グループ内で1つの要素をリーダーとして選び、これをいわば”グループ名”として管理します。(上図での”グループ1”や”グループ2”は例えば1や4になります。)
2. 実装
それでは実装していきます。変数名、メソッド名等はなるべくACLに沿って実装します。
2.1. コンストラクタ
まずクラスDSUを作成し、コンストラクタを実装します。
class DSU:
def __init__(self, n): # n:要素数
self._n = n
self.parent_or_size = [-1] * n
nは要素数で、インスタンス変数 _nに保持しておきます。
また、各要素についての情報を格納するリストparent_or_sizeを作成します。名前の示す通り、このリストの各要素parent_or_size[i]は、要素 i の parent (リーダー)もしくは要素 i の属するグループの size (大きさ)を表します。具体的には
-
parent_or_size[i]が負 : - 要素 i はグループのリーダーであり、属するグループの大きさは
abs(parent_or_size[i])
-
parent_or_size[i]が 0以上 : - 要素 i の属するグループのリーダーは
parent_or_size[i]
です。つまり初期化時点では全ての要素が、「自分をリーダーとする大きさ1のグループ(要素が自分だけのグループ)」に属しているということになります。
2.2. Find
操作FindはACLではleaderという名前で実装されています。このメソッドは要素を指定することで、その要素が属するグループのリーダーを返します。
def leader(self, a):
assert 0 <= a < self._n
if self.parent_or_size[a] < 0: return a # 負ならリーダー
self.parent_or_size[a] = self.leader(self.parent_or_size[a])
return self.parent_or_size[a]
まず、3行目でparent_or_size[a]が負ならば a はリーダーなのでそのままreturnします。そうでないならばparent_or_size[a]は a のリーダー (仮) です。なぜなら、グループの統合があった場合片方のリーダーはリーダーではなくなるからです。そこで、このリーダー(仮)から再帰的に 真の リーダーを探します。4行目で右辺を直接returnせずに代入することでリーダーの情報を更新しています。メモ化していると言ってもいいかもしれません。これによって次回以降の探索が短くなります。
2.3. Union
操作UnionはACLではmergeという名前で実装されています。このメソッドは要素を2つ指定することで、それらの属するグループを統合します。
def merge(self, a, b):
assert 0 <= a < self._n
assert 0 <= b < self._n
x, y = self.leader(a), self.leader(b)
if x == y: return x
if -self.parent_or_size[x] < -self.parent_or_size[y]: x, y = y, x
self.parent_or_size[x] += self.parent_or_size[y] # xの大きさにyの大きさを加算
self.parent_or_size[y] = x # yのリーダーはx
return x
まず、a, bそれぞれのリーダーx, yを求めます。これらが一致していれば、すでにa, bは同じグループに属しているので何もする必要はありません(5行目)。そうでない場合、yのグループをxのグループに統合します。この時、6行目のようにすることで常に小さいグループを大きいグループへ統合するようにします。yのグループメンバーはリーダーの情報を更新する必要があるので、これによって計算量を減らすことができます。
2.4. その他のメソッド
ACLのDSUには他にもいくつかのメソッドが実装されているので、それらも実装していきます。
same
メソッドsameは要素を2つ指定することで、それらが同じグループに属しているかの真偽値を返します。
def same(self, a, b):
assert 0 <= a < self._n
assert 0 <= b < self._n
return self.leader(a) == self.leader(b)
size
メソッドsizeは指定した要素が属するグループの大きさ(要素数)を返します。
def size(self, a):
assert 0 <= a < self._n
return -self.parent_or_size[self.leader(a)]
groups
メソッドgroupsは全要素をグループごとにまとめたリストを返します。
def groups(self):
leader_buf = [self.leader(i) for i in range(self._n)]
result = [[] for _ in range(self._n)]
for i in range(self._n): result[leader_buf[i]].append(i)
return [r for r in result if r != []]
2.5. まとめ
全てをまとめたものを置いておきます。
class DSU:
def __init__(self, n):
self._n = n
self.parent_or_size = [-1] * n
def merge(self, a, b):
assert 0 <= a < self._n
assert 0 <= b < self._n
x, y = self.leader(a), self.leader(b)
if x == y: return x
if -self.parent_or_size[x] < -self.parent_or_size[y]: x, y = y, x
self.parent_or_size[x] += self.parent_or_size[y]
self.parent_or_size[y] = x
return x
def same(self, a, b):
assert 0 <= a < self._n
assert 0 <= b < self._n
return self.leader(a) == self.leader(b)
def leader(self, a):
assert 0 <= a < self._n
if self.parent_or_size[a] < 0: return a
self.parent_or_size[a] = self.leader(self.parent_or_size[a])
return self.parent_or_size[a]
def size(self, a):
assert 0 <= a < self._n
return -self.parent_or_size[self.leader(a)]
def groups(self):
leader_buf = [self.leader(i) for i in range(self._n)]
result = [[] for _ in range(self._n)]
for i in range(self._n): result[leader_buf[i]].append(i)
return [r for r in result if r != []]
3. 使用例
n = 8 # 全要素数
d = DSU(n)
d.merge(0, 1)
d.merge(1, 3)
d.merge(0, 4)
d.merge(5, 6)
d.merge(3, 7)
print(d.groups()) # [[0, 1, 3, 4, 7], [2], [5, 6]]
print(d.leader(3)) # 0
print(d.same(1, 7)) # True
print(d.same(0, 5)) # False
print(d.size(6)) # 2
4. 問題例
AtCoder Library Practice Contest A "Disjoint Set Union"
AtCoder Typical Contest 001 B "Union Find"
5. おわりに
DSUの仕組みの解明からPythonでの実装までができました。また、実装上では様々な工夫がされていることがわかりました。特に必要な情報を一つの配列で表現する工夫には感動しました。
説明の間違いやバグ、アドバイス等ありましたらお知らせください。