AVL木
AVL木は平衡二分[探索]木の一種です。以下は平衡方法の概要です。
まずノード$x$の「高さ」を、そのノードから葉方向に行くときに通るノード数の最大値とし、$\mathrm{height}(x)$と表すことにします。便宜上存在しないノードの高さは$0$とします。
次にあるノードの平衡係数を、$(\mathrm{height}(\text{左の子}) - \mathrm{height}(\text{右の子}))$と定義します。
AVL木では全てのノードにおいて平衡係数の絶対値が高々$1$になるようにします。こうすることで全体の高さは$O(\log N)$になります。$(f(x)=$高さが$x$なAVL木に含まれる最小ノード数とすると$f(x + 2) = f(x + 1) + f(x) + 1$となり、$f$がフィボナッチ数列(指数オーダー)以上になるので)
また、ある部分木内のノードが全てこの条件を満たす時、その「部分木がAVL木である」と表現することにします。便宜上空木もAVL木であるとします。
この記事はこのAVL木の条件が保たれる証明(とまでは厳密ではない説明かもしれない)に重点を置いているので、実際に実行する操作は文字の量に比べてそんなに多くありません。
実際に実行する操作は茶色で示します。
balance
まず以下の要件を満たす関数balanceを作ります。
- ノード$x$を引数にとる
- $x$の左の子以下の部分木及び右の子以下の部分木はAVL木であることを仮定する
- $x$の平衡係数の絶対値が高々2であることを仮定する。(したがって$x$以下の部分木は必ずしもAVL木とは限らない)
- どうにかして$x$以下の部分木をAVL木にする(根は別のノードになってもいい)
- $x$以下の部分木の高さを変えない、または$1$だけ減らす
- $O(1)$で動作する
実際の方法は以下の通りです
- $x$の平衡係数の絶対値が1以下なら元からAVL木なので放っておく
- 平衡係数が$-2$な場合、$2$な場合と左右対称なことをすればよいので省略、考えるべきは平衡係数が$2$の場合。
- とりあえず$x$を右回転してみます、右回転というのは以下のような感じの操作です。
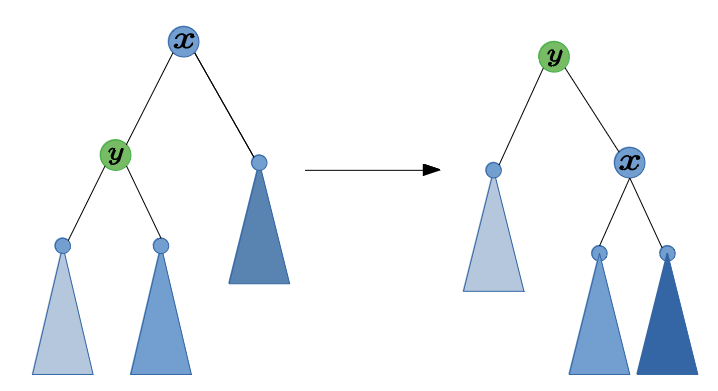
青いのは中に何が入ってるかわからないけどAVL木な部分木です。
平衡係数が$2$だったということはなんとなく今まで左側が深かったのでいい感じで平衡されそうな気がします。
$x$の平衡係数が$2$、$y$以下の部分木がAVL木という仮定から3つの青い部分木の高さ関係としてあり得るのは以下の3つのみです。- ある$h$を用いて左から順に$(h + 1, h, h)$と表される場合
回転後$x,y$の平衡係数はそれぞれ$0,0$、全体の部分木の高さは$h + 3$→$h + 2$なのでこれでokです。 - ある$h$を用いて左から順に$(h + 1, h + 1, h)$と表される場合
回転後$x,y$の平衡係数はそれぞれ$1,-1$、全体の部分木の高さは$h + 3$→$h + 3$なのでこれでokです。 - ある$h$を用いて左から順に$(h, h + 1, h)$と表される場合
回転後$x,y$の平衡係数はそれぞれ$1,-2(!)$なのでダメです。
元の $y$ の平衡係数が$-1$なのが悪い → 右回転する前に $y$ を左回転(右回転の左右対称版)しとけばいいんじゃね、となります。
左回転はさっきの逆で、$a$を左回転するとは以下のような感じです。
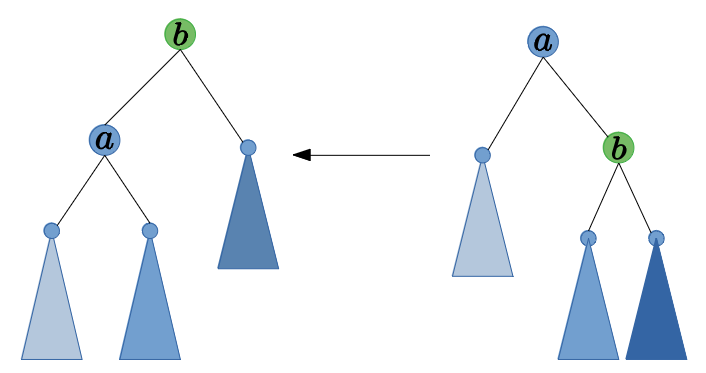
一番左の部分木の高さが$h$、$b$の高さが$h + 1$、$b$以下の部分木がAVL木であることを考えると3つの部分木の高さが以下のいずれかです- 左から順に$(h, h - 1, h)$な場合
回転後、$a,b$の平衡係数はそれぞれ$1, 1$、元の右回転の時の$3$つの部分木の高さは$(h + 1, h + 1, h)$で、そのケースは右回転すれば大丈夫なことが分かっているのでok - 左から順に$(h, h, h)$な場合
回転後、$a,b$の平衡係数はそれぞれ$0, 1$、元の右回転の時の$3$つの部分木の高さは$(h + 1, h, h)$で、そのケースは右回転すれば大丈夫なことが分かっているのでok - 左から順に$(h, h, h - 1)$な場合
回転後、$a,b$の平衡係数はそれぞれ$0, 2(!)$、元の右回転の時の$3$つの部分木の高さは$(h + 1, h - 1, h)$
これはまだ右回転して大丈夫なことが分かっていないので、元の右回転に戻ってこうなった場合を考えてみます。
- 左から順に$(h, h - 1, h)$な場合
- ある$h$を用いて左から順に$(h + 1, h - 1, h)$と表される場合
右回転後$x,y$の平衡係数はそれぞれ$-1, 0$、全体の部分木の高さは$h + 3$→$h + 2$なのでokです。めでたしめでたし
- ある$h$を用いて左から順に$(h + 1, h, h)$と表される場合
場合分けが多いですが、これは結局うまくいく証明のためでつまるところやるべきは
-
自分の平衡係数が$2$なら
- 左の子の平衡係数が$-1$ならば左の子を左回転
- (上の条件に関わらず)自身を右回転する
-
自分の平衡係数が$-2$なら
- 右の子の平衡係数が$1$ならば右の子を右回転
- (上の条件に関わらず)自身を左回転する
というそこそこシンプルなことだけです。
merge
本題です。ここから上のbalance関数をところどころ使います。
関数merge$(l,r)$
- $l,r$はノード
- $l$及び$r$以下の部分木はAVL木で、それぞれ親を持たないことを仮定する(空かもしれない)
- どうにかして$l$の木と$r$の木の要素の順序を保ったままこの順に$1$つのAVL木にまとめ、その根を戻す
- $O(\log N)$で動作する。($N$は$l,r$に入ってるノード数の合計)
この関数を作るために補助関数を作ります
merge_with_root
関数merge_with_root($l,\mathrm{root},r$)
- 引数$l,\mathrm{root},r$はノード
- $l$及び$r$以下の部分木はAVL木で、それぞれ親を持たないことを仮定する(空かもしれない)
- $\mathrm{root}$は孤立していて(親も子もいない)、空でないことを仮定する
- $l$の木$,\mathrm{root},r$の木の要素の順序を保ったままどうにかしてこの順に$1$つにまとめたAVL木の根を戻す
- 戻すAVL木の高さは$\max(\mathrm{height}(l), \mathrm{height}(r))$と等しいか、それに$1$を加えたものである。
- $O(|\mathrm{height}(l) - \mathrm{height}(r)|)$で動作する
好きに使っていいノード$\mathrm{root}$が与えられたバージョンです。
方法は以下の通りです。
- $|\mathrm{height}(l) - \mathrm{height}(r)| \le 1$の場合
$\mathrm{root}$の左子,右子をそれぞれ$l,r$にして$\mathrm{root}$を戻します。終わり。 - $\mathrm{height}(l) - \mathrm{height}(r) \gt 1$の場合
$l$がデカすぎるのでそのままやると返す木がAVL木でなくなってしまう、困った
merge_with_root$(l$の右子$, \mathrm{root}, r)$を再帰的に呼び、戻り値を$l$の右子に設定する。
$l$に対してbalanceを呼び、その戻り値を戻す。
この手順で関数の仕様である「戻すAVL木の高さは$\max(\mathrm{height}(l), \mathrm{height}(r))$と等しいか、それに$1$を加えたものである。」が満たされるのは自明ではない、以下証明。
$\mathrm{height}(l) \ge \mathrm{height}(r) + 2$であり$l$はAVL木なので$\mathrm{height}(l$の右子$) \ge \mathrm{height}(r)$である。これとmerge_with_rootの仕様より、再帰呼び出しによって$\mathrm{height}(l$の右子$)$は変わらないか$1$だけ増えることが分かる。- $\mathrm{height}(l$の右子$)$が変わらない場合
balanceは何もしないので戻るのは$l$そのものだから高さは変わらないか$1$増えるだけである。 - $\mathrm{height}(l$の右子$)$が$1$増える場合
balanceによって$\mathrm{height}(l$の右子$)$はそこから変わらないか$1$だけ減る(balanceの仕様より)ので全体として$\mathrm{height}(l$の右子$)$は変わらないか$1$増えるだけで、$\mathrm{height}(l)$も変わらないか$1$増えるだけである。
- $\mathrm{height}(l$の右子$)$が変わらない場合
- $\mathrm{height}(l) - \mathrm{height}(r) \lt -1$の場合
上の左右対称版
再帰以外は$O(1)$で、一回再帰を潜るごとに$|\mathrm{height}(l) - \mathrm{height}(r)|$は$2$ずつ減り、$1$以下になると終了するのでこれは$O(|\mathrm{height}(l) - \mathrm{height}(r)|)$で動作します。
ふぅ... mergeに戻ります
一応コーナーケースとして$l$又は$r$が空だったら、他方を返します。
以下両方ちゃんとノードがある場合。
基本的には$l$の中で一番右のノードを取り出してきてそれを$\mathrm{root}$にしてmerge_with_root$(l, \mathrm{root}, r)$を呼びます。
$l$の中で一番右のノードを取り出すのは以下の要領でできます。
- $l$から始めて、右の子が存在する限り右に潜る
- 終わったときには右の子はないので、(存在するなら)左の子を親の右の子にして、自身は孤立させる。
これで終わりです。一回潜ってあとはmerge_with_rootを呼び出すだけなので$O(\log N)$です。
split
splitがないとmergeだけあっても楽しくないですね
splitは、AVL木をstd::setのような大小関係を持った要素の集合として使うか、何かの列を管理するものとして使うかによって少しインターフェースが変わりますが、今回は後者でいきます。
関数split$(x, i)$
- $x$はノード
- $i$は整数で$0 \le i \le (x$の部分木に含まれるノード数$)$
- $x$の部分木のうち左から$i$個だけを(順序を保って)含むAVL木$L$と、それ以外を(順序を保って)含むAVL木$R$のペアを戻す
- $\mathrm{height}(L) \le \mathrm{height}(x) + 1$を満たす
- $\mathrm{height}(R) \le \mathrm{height}(x) + 1$を満たす
- $O(\log N)$で動作する($N$は$x$の部分木に含まれるノード数)
手順です
- $x$が空なら$(L,R)=($空$,$空$)$を返す
- $x$から2つの子供を切り離します。(以後も簡単のため「$x$の左子」などを$x$の左子だったノードという意味で使います)
- $x$の左子以下にあるノード数を$\mathrm{lsize}$とする
- $i = \mathrm{lsize}$の場合
このノードのすぐ左で切るのが正しいです
$(L,R) = (x$の左子$,$ merge_with_root$($空$, x, x$の右子$))$として戻す- $\mathrm{height}(x$の右子$) \le \mathrm{height}(x) - 1,$ merge_with_rootの仕様より$\mathrm{height}(R) \le \mathrm{height}(x)$
- $\mathrm{height}(L) = \mathrm{height}(x$の右子$) \le \mathrm{height}(x) - 1$
よってsplitの$L,R$の高さに関する仕様を満たす。
- $i \lt \mathrm{lsize}$の場合
左の子に潜って切りに行きます
$(l, r) = $ split$(x$の左子$, i)$と呼び出す
$(L, R) = (l, $ merge_with_root$(r, x, x$の右子$))$として戻す
$\mathrm{height}(x$の左子$) \le \mathrm{height}(x) - 1,$ splitの仕様より$\mathrm{height}(l) \le \mathrm{height}(x)$かつ$\mathrm{height}(r) \le \mathrm{height}(x)$
$\mathrm{height}(x$の右子$) \le \mathrm{height}(x) - 1,$ merge_with_rootの仕様より$\mathrm{height}(R) \le \mathrm{height}(x) + 1$
よってsplitの$L,R$の高さに関する仕様を満たす。 - $i \gt \mathrm{lsize}$の場合
さっきの左右対称。splitを再帰するときに$i$から$\mathrm{lsize + 1}$を引くのを忘れないように
- $i = \mathrm{lsize}$の場合
このsplitは一見、再帰が最悪$\Theta(\log N)$回あり各呼び出しでmerge_with_rootを呼び出すから最悪$\Theta((\log N)^2)$かかるように見える。
しかし、再帰的に左の子に潜る場合を考えたとき(右に潜る場合も左右対称で全く同じ議論ができるのでそっちは省略)
- $r$(再帰呼び出しの戻り値の右側)と、$x$の右子をmerge_with_rootするわけだが
- $\mathrm{height}(r) \gt \mathrm{height}(x$の右子$)$の場合
splitの仕様より、$\mathrm{height}(r) \le \mathrm{height}(x$の左子$) + 1$
また、$x$以下の部分木はAVL木であったから$\mathrm{height}(x$の左子$) \le \mathrm{height}(x$の右子$) + 1$である。
よって$\mathrm{height}(r) \le \mathrm{height}(x$の右子$) + 2$であり、$\mathrm{height}(r) \gt \mathrm{height}(x$の右子$)$であったので$|\mathrm{height}(r) - \mathrm{height}(x$の右子$)| \le 2$。
したがってmerge_with_rootの計算量はこの場合$O(1)$になる。 - $\mathrm{height}(r) \le \mathrm{height}(x$の右子$)$の場合
merge_with_rootの要件より、$\mathrm{height}(R) \ge \mathrm{height}(x$の右子$)$
よってmerge_with_rootにかかる時間は高々$\mathrm{height}(R) - \mathrm{height}(r)$だから全ての再帰呼び出しでかかるmerge_with_rootの合計は高々一番最初の呼び出しが戻す$R$の高さであり、$O(\log N)$である。
- $\mathrm{height}(r) \gt \mathrm{height}(x$の右子$)$の場合
merge_with_root以外は$O(1)$だからちゃんと$O(\log N)$で動作しました。
実装
実装はそんなに重くなくて、15分くらいあれば書けると思います。
子がない場合nullptrの代わりに高さ0, サイズ0のダミーノードを子にしておくと楽です
以下は簡易的な数列管理のAVL木で、AVL(n)でn一つからなる数列を生成,AVL::mergeとか.splitとかでいろいろできます。(未verify、バグってたらごめん)
struct AVL {
struct Node {
Node *l;
Node *r;
int val;
int size;
int height;
Node *fetch() {
size = 1 + l->size + r->size;
height = 1 + std::max(l->height, r->height);
return this;
}
Node *rotate_l() {
Node *new_root = r;
r = new_root->l;
new_root->l = this;
return fetch(), new_root->fetch();
}
Node *rotate_r() {
Node *new_root = l;
l = new_root->r;
new_root->r = this;
return fetch(), new_root->fetch();
}
int height_diff() { return l->height - r->height; }
Node *balance() {
int dif = height_diff();
if (dif == 2) {
if (l->height_diff() < 0) l = l->rotate_l();
return rotate_r();
} else if (dif == -2) {
if (r->height_diff() > 0) r = r->rotate_r();
return rotate_l();
} else return fetch();
}
};
static Node *nodes, *NONE, *removed_tmp;
static int head;
Node *root = NONE;
AVL () {
if (!head) nodes[head++] = {NONE, NONE, 0, 0, 0};
}
AVL (int val) : AVL() {
root = &(nodes[head++] = {NONE, NONE, val, 1, 1});
}
AVL (Node *root) : root(root) {}
static Node *remove_rightest(Node *node) {
if (node->r != NONE) {
node->r = remove_rightest(node->r);
return node->balance();
} else return (removed_tmp = node)->l;
}
static Node *merge_with_root(Node *l, Node *root, Node *r) {
int dif = l->height - r->height;
if (-1 <= dif && dif <= 1) {
root->l = l;
root->r = r;
return root->fetch();
} else if (dif > 0) {
l->r = merge_with_root(l->r, root, r);
return l->balance();
} else {
r->l = merge_with_root(l, root, r->l);
return r->balance();
}
}
static Node *merge(Node *l, Node *r) {
if (l == NONE) return r;
l = remove_rightest(l);
return merge_with_root(l, removed_tmp, r);
}
static std::pair<Node *, Node *> split(Node *node, int index) {
if (node == NONE) return {NONE, NONE};
Node *l = node->l;
Node *r = node->r;
node->l = node->r = NONE;
int lsize = l->size;
if (index < lsize) {
auto tmp = split(l, index);
return {tmp.first, merge_with_root(tmp.second, node, r)};
} else if (index > lsize) {
auto tmp = split(r, index - lsize - 1);
return {merge_with_root(l, node, tmp.first), tmp.second};
} else return {l, merge_with_root(NONE, node, r)};
}
static void print_all(Node *node) {
if (node == NONE) return;
print_all(node->l);
printf("%d ", node->val);
print_all(node->r);
}
// wrappers
static AVL merge(AVL l, AVL r) { return AVL(merge(l.root, r.root)); }
std::pair<AVL, AVL> split(int index) {
auto tmp = split(root, index);
return {AVL(tmp.first), AVL(tmp.second)};
}
void print_all() {
print_all(root);
puts("");
}
};
AVL::Node *AVL::nodes = (Node *) malloc(sizeof(Node) * 1000000), *AVL::NONE = nodes, *AVL::removed_tmp;
int AVL::head = 0;
終わり
balanceの二重回転の辺りとかAVL木って結構危なっかしくみえるね
参考になりましたありがとう
https://tubo28.me/compprog/algorithm/avl_tree/
http://wwwa.pikara.ne.jp/okojisan/avl-tree/index.html
https://qiita.com/mikecat_mixc/items/e9f8248de2ae7f7a0a29
https://ja.coursera.org/lecture/data-structures/split-and-merge-22BgE