AVL木の回転(要素の挿入や削除のしかた)

基本事項

二分探索木

二分探索木は、二分木(各ノードが高々2個の子を持つ根付き木)の一種であり、「左の子が持つ値は自分が持つ値以下であり、右の子が持つ値は自分が持つ値以上である」という特徴を持つ。また、各ノードは1個のデータを保持する。
この特徴により、指定された値の探索や挿入の効率を上げることができることが期待される。

しかし、工夫をしないと要素を挿入する順番によっては木が無駄に高くなってしまい、効率が上がらないことがある。
そこで、適当に木を変形してバランスをとり、ノード数に対して木が高くなり過ぎないようにするのが平衡二分探索木である。

二分木の高さ

二分木の高さとは、根から葉に行くパス(各ノードを高々1回しか通らない経路)上の辺の数の最大値である。
根だけからなる二分木の高さは0である。

要素の検索

1. 木の根に注目する。
2. 注目しているノードが存在するかを確認する。存在しない場合、検索は失敗して終了する。
3. 注目しているノードが保持しているデータと検索したいデータの大小関係を比較する。
   • ノードが保持しているデータと検索したいデータが一致した場合は、検索は成功して終了する。
   • ノードが保持しているデータの方が大きい場合は、注目しているノードの左の子に注目し、2に戻る。
   • 検索したいデータの方が大きい場合は、注目しているノードの右の子に注目し、2に戻る。

要素の追加

1. 要素の検索と同様の要領でノードへの注目を切り替えていく。
2. 注目しているノードが存在しなくなったら、そこに追加するデータを保持している新しいノードを挿入する。
3. 注目しているノードが保持しているデータと追加するデータが一致した場合は、
   • データの重複を許さない場合は、追加処理をキャンセルして終了する。
   • データの重複を許す場合は、左か右のあらかじめ決めておいた方の子に注目する。

要素の削除

削除したいノードの子が1個以下の場合は、そのノードを削除し、子がある場合はその子を削除するノードがあった場所に接続する。
削除したいノードが子を2個持つ場合は、「左側の子を根とする部分木の中で最大のデータを持つノード」または「右側の子を根とする部分木の中で最小のデータを持つノード」のデータを削除したいノードにコピー(上書き)し、代わりにデータをコピーされたノードを削除する。このとき、データをコピーされるノードは最大または最小のデータを持つので、二分探索木の定義より子は高々1個である。

AVL木

AVL木は平行二分探索木の一種であり、「どのノードについても、それぞれの子を根とする部分木の高さの差(以下、子の高さ)が1以下」という条件がある。なお、子が無い場合は、ここでは便宜上その子の高さは-1とみなす。
実装においては、左の子の高さと右の子の高さの差を各ノードに記録し、その情報を用いてバランスの調整を行うとよい。
この記事では、左の子の高さから右の子の高さを引いた値をノードの「子の高さの差」とする。

木の回転

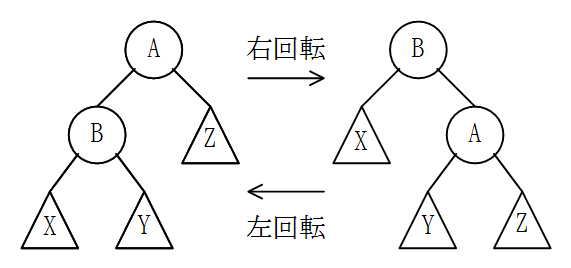
二分探索木における木の回転とは、二分探索木の各ノードが持つ値の大小関係の条件を満たしたまま木を変形する操作である。
親と子の位置関係を変えることで、右回転の場合は

• 左にある部分木は、位置が1段高くなる
• 真ん中にある部分木は、親が変わり、縦の位置は変わらない
• 右にある部分木は、位置が1段低くなる

という効果が得られる。左回転の場合はその逆である。

AVL木の回転

AVL木を回転させる場合、同時にノードに記録されている各部分木の高さの差を更新すると良い。
左回転と右回転は対称な操作であるため、ここでは右回転を考える。
回転をするノード(以下、ノードA)の子の高さの差をa、回転をするノードの左の子(以下、ノードB)の高さの差をbとする。なお、回転をするノードに左の子が無い場合、右回転は成立しない。

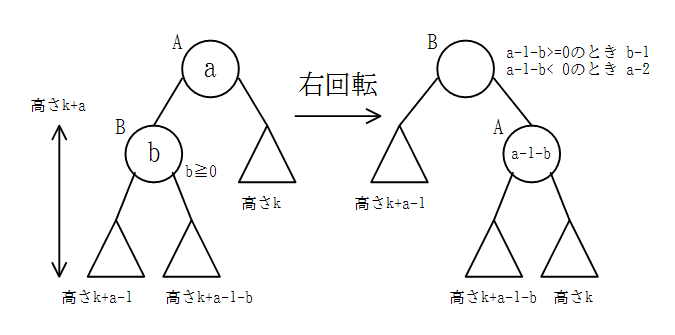
b≧0のとき

ノードAの右の子の高さをkとすると、b≧0よりノードBの左の子の高さはノードBの右の子の高さ以上なので、各ノードの子の高さの差に基づいて計算をすると、ノードBの左の子の高さはk+a-1、ノードBの右の子の高さはk+a-1-bと求まる。
この状態から右回転を行うと、ノードAの左の子が高さk+a-1の部分木に、ノードBの右の子がノードAになるので、これに基いて計算をすると回転後のノードAおよびノードBの子の高さの差がわかる。
このとき、ノードBの右の子の高さ、すなわちノードAを根とする部分木の高さはノードAの各子の高さの大小関係、すなわちノードAの子の高さの差の符号に依存するので、場合分けを行う。また、ノードBの右の子の高さはノードAの子を根とする低くない方の部分木の高さにノードAの分の1を加えたものである。
すると、回転後のノードAの子の高さの差はa-1-b、ノードBの子の高さの差はa-1-b >= 0のときb-1、a-1-b < 0のときa-2であるとわかる。

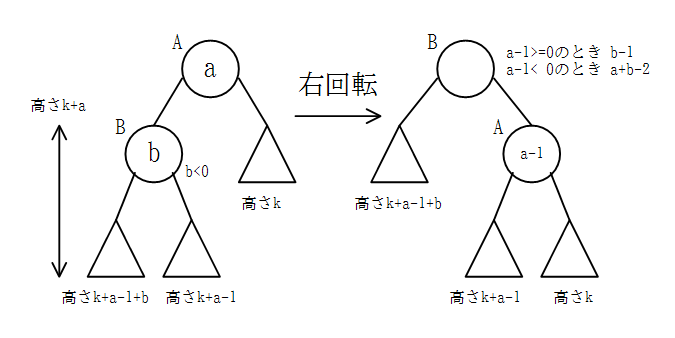
b<0のとき

b≧0のときと同様に計算をすると、回転後のノードAの子の高さの差はa-1、ノードBの子の高さの差はa-1 >= 0のときb-1、a-1 < 0のときa+b-2であるとわかる。

対称性の利用

右回転の操作の左右を反転することで、左回転を行うことができる。
左右反転によって、子の位置関係だけでなく、子の高さの差の符号も反転するので注意が必要である。

AVL木における挿入や削除と回転

挿入や削除を行うと、要素数が変わるので、子の高さの差が変わることがある。
子の高さの差の絶対値が1を超えた場合は、回転を行ってバランスをとる必要がある。

挿入 (要素が増える場合) における法則

葉に到達し、新たにノードを作成して挿入すると、明らかに木の高さが大きくなる。

挿入によって子の高さが大きくなった場合は、以下のようになる。

• もともと低い側の子の高さが大きくなった場合
  子の高さの差の絶対値は小さくなるが、木の高さは変わらない。
  
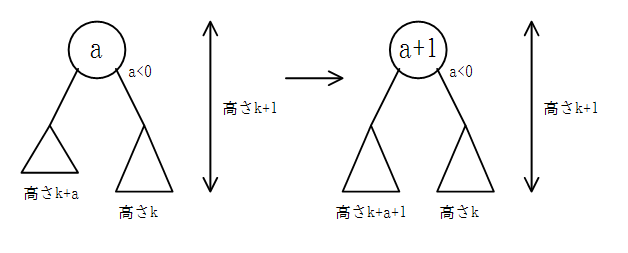
• もともと低くない(高い、または同じ高さ)側の子の高さが大きくなった場合
  木の高さが大きくなる。また、子の高さの差の絶対値が大きくなり、1を超えて回転操作が必要となる場合がある。
  

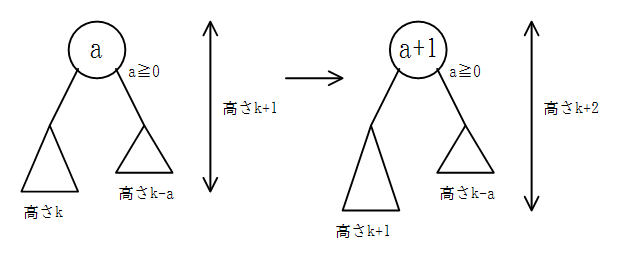
挿入によって子の高さが変わらなかった場合は、明らかに木の高さは変わらない。
また、挿入(回転を含まない)によって子の高さが減ることは無い。

削除 (要素が減る場合) における法則

高々1個の子を持つノードを削除すると、明らかに木の高さが小さくなる。

削除によって子の高さが小さくなった場合は、以下のようになる。

• もともと高くない(低い、または同じ高さ)側の子の高さが小さくなった場合
  木の高さは変わらないが、子の高さの差の絶対値が大きくなり、1を超えて回転操作が必要となる場合がある。
  
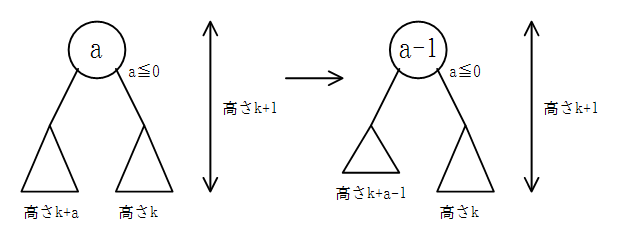
• もともと高い側の子の高さが小さくなった場合
  木の高さが小さくなる。また、子の高さの差の絶対値は小さくなる。
  

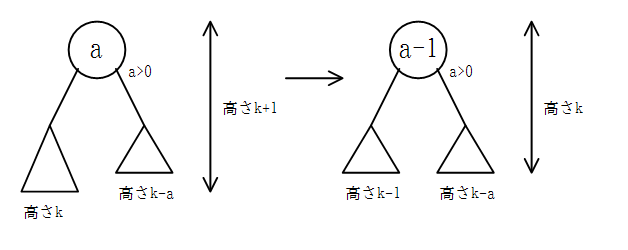
削除によって子の高さが変わらなかった場合は、明らかに木の高さは変わらない。
また、削除(回転を含まない)によって子の高さが増えることはない。

回転操作の法則

ここでは、左の子の高さが右の子の高さより2大きくなり、右回転をする場合について扱う。
左の子の高さが右の子の高さより2小さくなった場合は左回転をするが、これは対称であるので省略する。
また、1回の挿入や削除によって木の高さは高々1しか変化しないので、正しく回転操作を行っていれば子の高さの差の絶対値が3以上になることは無い。
さらに、回転によって上下関係が変わる2個のノードより下にある部分木は影響を受けないので、AVL木である部分木がバランスを取るための回転によってAVL木でなくなることは無い。

以下、左の子の高さが右の子の高さより2大きくなったノードをノードA、ノードAの左の子をノードBとする。
ノードAの左の子の高さは右の子の高さより大きいので、ノードBは存在する。
また、ノードBの子の高さの差の絶対値はAVL木の定義に従い、1以下とする。

なお、これらの法則は、子の高さの差の変化が挿入によって生じたか削除によって生じたかに関係なく、子の高さの差のみを見て適用が可能である。

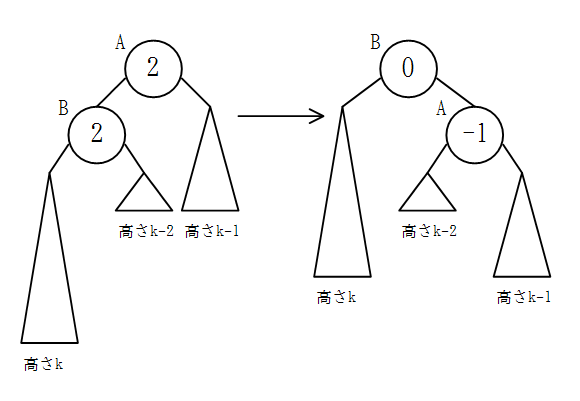
ノードBの子の高さの差が2のとき

これは「ノードBの子の高さの差の絶対値が1以下」という条件を満たしていないが、後で使うため解析を行っておく。

左端の部分木が一番高く、中央の部分木と右端の部分木はそれより高さが2小さい。
この状態で右回転を行うと、左端の部分木の位置は上がり、右端の部分木の位置は下がるので、左端と右端の部分木の一番下の葉の位置が揃い、中央の部分木の一番下の葉はそれより上にあるので、バランスが取れる。
よって、単純にノードAに右回転を行えばいいことがわかる。
また、このとき回転前のノードA(回転後のノードB)を根とする木の高さは1減る。

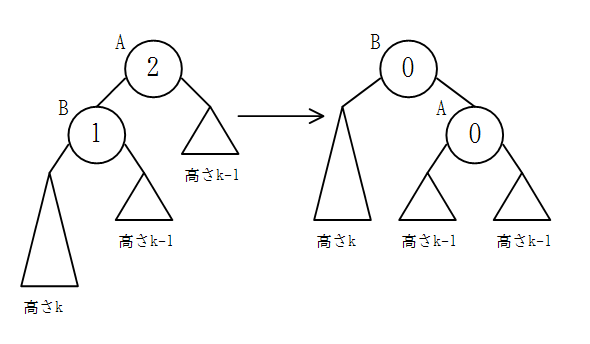
ノードBの子の高さの差が1のとき

左端の部分木が一番高く、中央の部分木はノードBの子の高さの差より左端の部分木より高さが1小さい。
右端の部分木、すなわちノードAの右の子を根とする部分木は、中央の部分木よりさらに高さが1小さいことがわかる。
この状態で右回転を行うと、左端の部分木の位置は上がり、右端の部分木の位置は下がるので、全ての部分木の一番下の葉の位置が揃い、バランスが取れる。
よって、単純にノードAに右回転を行えばいいことがわかる。
また、このとき回転前のノードA(回転後のノードB)を根とする木の高さは1減る。

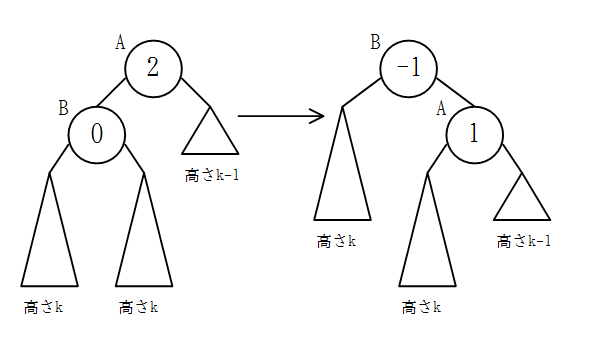
ノードBの子の高さの差が0のとき

左端の部分木と中央の部分木の高さは同じであり、右端の部分木はそれらより高さが2小さいことがわかる。
この状態で右回転を行うと、左端の部分木の位置は上がり、右端の部分木の位置は下がるので、中央と左端、中央と右端の部分木の一番下の葉の位置の差がそれぞれ1になり、バランスが取れる。
よって、単純にノードAに右回転を行えばいいことがわかる。
また、このとき回転前のノードA(回転後のノードB)を根とする木の高さは変わらない。

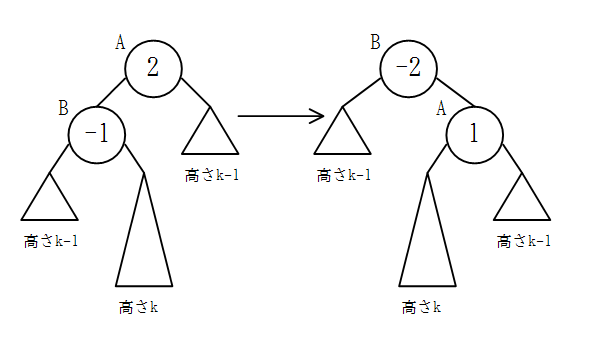
ノードBの子の高さの差が-1のとき

単純にノードAに右回転を行うだけでは、ただでさえ中央の部分木より上にある左端の部分木がさらに上に上がってしまい、バランスを取ることができない。

そこで、まずノードBに左回転を行う。
ノードBの右側の子をノードCとする。ノードBの子の高さの差が負なので、ノードCは存在する。また、ノードCの子の高さの差の絶対値はAVL木の定義に従い、1以下とする。

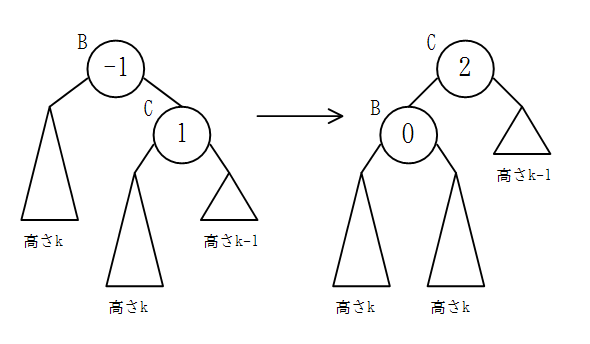
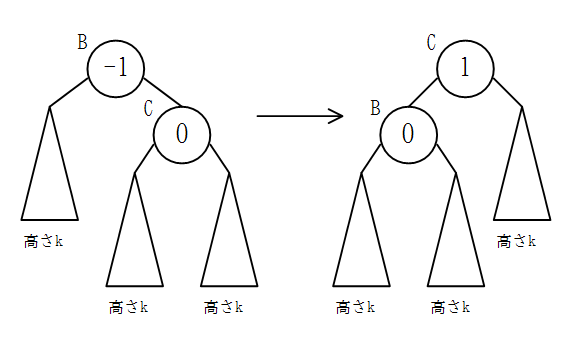
ノードCの子の高さの差が1のとき

左端の部分木と右端の部分木の一番下の葉がそれぞれ中央の部分木より1だけ上にあることがわかる。
この状態で左回転を行うと、左端の部分木は下がり、右端の部分木は上がるので、ノードBがあった位置に来るノードCの子の高さの差は2になる。
また、中央の部分木の一番下の葉の位置は変わらないので、ノードBを根とする部分木の高さは変わらず、ノードAの子の高さの差も変化しない。
従って、解析を行っておいた「ノードBの子の高さの差が2のとき」の法則(ノードAに右回転を行えばよい)に帰着できる。

ノードCの子の高さの差が0のとき

中央の部分木と右端の部分木の一番下の葉が同じ位置にあり、左端の部分木の一番下の葉はそれより1だけ上にあることがわかる。
この状態で左回転を行うと、左端の部分木は下がり、右端の部分木は上がるので、ノードBがあった位置に来るノードCの子の高さの差が1になる。
また、中央の部分木の一番下の葉の位置は変わらないので、ノードBを根とする部分木の高さは変わらず、ノードAの子の高さの差も変化しない。
従って、「ノードBの子の高さの差が1のとき」の法則(ノードAに右回転を行えばよい)に帰着できる。

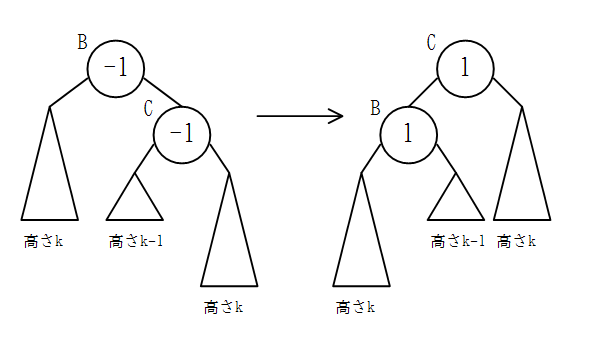
ノードCの子の高さの差が-1のとき

左端の部分木と中央の部分木の一番下の葉が同じ位置にあり、右端の部分木の一番下の葉はそれより1だけ下にあることがわかる。
この状態で左回転を行うと、左端の部分木は下がり、右端の部分木は上がるので、ノードBがあった位置に来るノードCの子の高さの差が1になる。
また、右端の部分木の一番下の葉の位置に左端の部分木の一番下の葉が来るので、ノードBを根とする部分木の高さは変わらず、ノードAの子の高さの差も変化しない。
従って、「ノードBの子の高さの差が1のとき」の法則(ノードAに右回転を行えばよい)に帰着できる。

回転の法則のまとめ

• 子の高さの差の絶対値が2になったら、高い方の子から低い方の子の方向に回転をすればよい。
• ただし、高い方の子の高さの差の符号が注目しているノードの子の高さの差の符号と逆(0は含まない)なら、その子を先に外側に回転してから注目しているノードの回転を行う。

回転と木の高さの変化

挿入後の回転

挿入後に回転が発生するのは、高い方の子の高さが挿入によって大きくなった場合であり、この場合は木の高さも増えている。
子の高さが同じ時は子の高さが1増えても子の高さの差の絶対値は1になるだけなので回転は発生せず、低い方の子の高さが挿入によって増えた場合は子の高さの差の絶対値が減るので回転は発生しない。
このとき、回転によって木の高さが減ると、挿入によって増えた分と回転によって減った分が相殺し、木の高さは変化しない。
また、回転によって木の高さが減らないのはノードBの子の高さの差が0のときのみであるが、これは挿入した場合は発生しない。以下に示す。

まず、回転が行われるということは、ノードBの木の高さが増えているはずである。
挿入後に木の高さが増えるのは、

• 新たにノードを作成して挿入した場合
• もともと低くない(高い、または同じ高さ)側の子の高さが大きくなった場合

である。
新たにノードを作成して挿入した場合は、ノードBを根とする部分木の高さは0なので、ノードAの子の高さの差は1以下になり、回転は発生しない。
もともと低くない(高い、または同じ高さ)側の子の高さが大きくなった場合は、さらに回転が発生する場合と回転が発生しない場合に分けられる。
回転が発生しない場合は、子の高さの差の絶対値が増えるので、子の高さの差は0にならない。
回転が発生する場合は、前述の解析より、ノードBの高い方の子の子の高さの差が0でない場合は、回転後にノードBがある場所のノードの子の高さの差は0にならない。
また、ノードBの高い方の子の子の高さの差が0である場合は回転後にノードBがある場所のノードの子の高さの差が0になるが、これはそもそもこれ以前に「回転対象のノードの左の子の子の高さの差が0であり、かつその子を根とする部分木の高さが挿入によって大きくなった」という状況がなければならず、この状況を作り出すのに利用することはできない。

従って、挿入時(子の高さが増えた時)はノードBの子の高さの差が0である状態で回転が行われることはなく、回転が行われた場合は必ず木の高さは変化しない。

削除後の回転

削除後に回転が発生するのは、低い方の子の高さが削除によって小さくなった場合であり、この場合は木の高さは変化していない。
子の高さが同じ時は子の高さが1減っても子の高さの差の絶対値は1になるだけなので回転は発生せず、高い方の子の高さが削除によって減った場合は子の高さの差の絶対値が減るので回転は発生しない。
また、このとき削除の影響を受けたのはノードBとは反対側の部分木なので、ノードBの子の高さの差は-1, 0, 1のどの場合も考えられる。

従って、削除時(子の高さが減った時)は、ノードBの子の高さの差が0のときは木の高さは変化せず、ノードBの子の高さの差が0でないときは木の高さが1小さくなる。

まとめ

子の高さの差の更新

左の子の高さが1大きくなった、または右の子の高さが1小さくなったときは子の高さの差に1を加え、
左の子の高さが1小さくなった、または右の子の高さが1大きくなったときは子の高さの差に-1を加える。
その後、子の高さの差の絶対値が1を超えた場合は回転を行う。

木の高さの更新(回転が発生しない場合)

木の高さが変化した子の変化前の高さ	挿入後の木の高さ	削除後の木の高さ
高い	(回転する)	減る
同じ	増える	変わらない
低い	変わらない	(回転する)

回転

回転の対象とその高い方の子で子の高さの差の符号が異なる場合(0は含まない)は、まず子を木の外側(左の子なら左回転、右の子なら右回転)に回転する。その後、回転の対象の回転を行って子の高さの差の絶対値を減らす。

挿入後回転が発生した場合は、木の高さは変わらない。
削除後回転が発生した場合は、高い方の子の子の高さの差が0のときは木の高さは変わらず、そうでないときは木の高さが減る。

実装の工夫

• 子の高さの差の更新を回転処理に含めることで、挿入や削除では子の高さの差の更新を意識せず、現在の子の高さの差を見て回転操作を行うだけでよくなった。
• 「要素の追加や削除による高さの更新」と「木の回転によるバランスの調整」を分けて考えることで、回転操作の制御を挿入と削除で共通にすることができた。

実装例

要素の重複を許さないAVL木の、C言語による実装例である。
rotate()関数は、is_rightが真の時は右回転を、偽の時は左回転を行う。
modify_tree()関数は、addが真の時はdataの追加を、偽のときはdataの削除を行う。

0 (整数)と入力すると、与えられた整数を木に追加する。
1 (整数)と入力すると、与えられた整数を木から削除する。
2と入力すると、木の構造を出力する。
3 (整数)と入力すると、与えられた整数を木に追加し、木の構造を出力する。
4 (整数)と入力すると、与えられた整数を木から削除し、木の構造を出力する。

```c:avl_tree.c`
#include
#include
#include

typedef struct node_tag {
int data;
int diff;
struct node_tag *child[2];
} node_t;

void rotate(node_t *node, int is_right) {
int l = is_right ? 0 : 1; / 「左の子」の添字 /
int r = is_right ? 1 : 0; / 「右の子」の添字 /
int sign = is_right ? 1 : -1; / 左回転の時はdiffの意味が反転する */
assert((node)->child[l] != NULL); / 回転に必要な子が無かったら死亡 */
if ((node)->child[l] != NULL) {
node_t left = (*node)->child[l];
int a = (node)->diff * sign, b = left->diff * sign, na, nb;
/ 高さの差の更新 */
if (b >= 0) {
if (a - 1 - b >= 0) {
nb = b - 1;
} else {
nb = a - 2;
}
na = a - 1 - b;
} else {
if (a - 1 >= 0) {
nb = b - 1;
} else {
nb = a + b - 2;
}
na = a - 1;
}
(node)->diff = na * sign;
left->diff = nb * sign;
/ 回転操作 */
(*node)->child[l] = (*node)->child[l]->child[r];
left->child[r] = *node;
*node = left;
}
}

/* 戻り値 = 高さの変化 */
int modify_tree(node_t **node, int data, int add) {
if (node == NULL) {
if (add) {
/ 新しい子を追加する */
*node = malloc(sizeof(node_t));
assert(*node != NULL);
if (node != NULL) {
/ 作成したノードを初期化する */
(*node)->data = data;
(node)->diff = 0; / 子は両方無い */
(*node)->child[0] = NULL;
(node)->child[1] = NULL;
}
/ 何もない所に子を作ったので、高さが増える */
return node != NULL;
} else {
/ 削除対象が見つからなかった */
return 0;
}
} else {
int l, delta, delta_sign;
node_t *next_node;
if (data == (node)->data) {
/ このノードのデータと同じ /
if (add) {
/ 重複したデータの挿入クエリなので、無視する /
return 0;
} else {
/ このノードを削除する */
if ((node)->child[1] == NULL) {
/ 右の子が無いので、左の子をこのノードの位置に持ってくる */
next_node = (*node)->child[0];
free(*node);
node = next_node;
/ 高さが1減る */
return -1;
} else if ((node)->child[0] == NULL) {
/ 左の子が無いので、右の子をこのノードの位置に持ってくる */
next_node = (*node)->child[1];
free(*node);
node = next_node;
/ 高さが1減る /
return -1;
} else {
/ 両方に子がある /
/ 左にある一番右のノードを探す */
for (next_node = (node)->child[0]; next_node->child[1] != NULL; next_node = next_node->child[1]);
/ そのノードの値をこのノードに持ってくる */
(node)->data = next_node->data;
/ そのノードを削除する (左に行く) */
l = 0;
delta_sign = 1;
delta = modify_tree(&(node)->child[l], next_node->data, add);
}
}
} else {
/ このノードは対象では無いので、子を処理する /
if (data < (*node)->data) {
/ このノードのデータより小さいので、左に行く /
l = 0; / 「左の子」の添字 /
delta_sign = 1; / diffの変化の方向 /
} else {
/ このノードのデータより大きいので、右に行く */
l = 1;
delta_sign = -1;
}
delta = modify_tree(&(node)->child[l], data, add);
}
if (delta != 0) {
/ 子の高さに変化があった */
int orig_diff = (node)->diff; / 子の高さが変わる前の高さの差 /
int do_rotate = 0, rotate_l, diff_sign, rotate_right; / 回転操作の情報 */
(node)->diff += delta * delta_sign; / 差を更新する */
if ((node)->diff > 1) {
/ 左が高すぎるので、右回転する /
do_rotate = 1; / 回転をする /
rotate_l = 0; / 「左の子」の添字 /
diff_sign = 1; / diffの意味 /
rotate_right = 1; / この回転は右回転か */
} else if ((node)->diff < -1) {
/ 右が高すぎるので、左回転する */
do_rotate = 1;
rotate_l = 1;
diff_sign = -1;
rotate_right = 0;
}
if (do_rotate) {
int child_diff = (node)->child[rotate_l]->diff;
/ 回転操作 */
if ((node)->child[rotate_l]->diff * diff_sign < 0) {
/ 左 -> 右 みたいな感じになっているので、まず子を回転する /
/ メインの回転の逆方向 */
rotate(&(node)->child[rotate_l], !rotate_right);
}
/ このノードを回転する /
rotate(node, rotate_right);
/ 子が高くなって回転をした場合は、高くなった分がその方向から減らされるから変わらない /
/ 子が低くなって回転をした場合は、低くなった分が反対方向から減らされるから減る /
/ ただし、高い方の子の高さの差が0の場合は、回転によって高さが減らない /
/ 挿入後の回転では、「高い方の子の高さの差が0、かつ高い方の子が高くなった」という場合は発生しない /
return delta < 0 && child_diff != 0 ? -1 : 0;
}
/ 高さの変化を返す /
if (delta > 0 && orig_diff == 0) {
/ 左右の高さが同じ状態で子の高さが増えたら、高さが増える /
/ 左右の高さが違う場合は、平らになるだけで高さは変わらないか、回転が行われここでは扱わない /
return 1;
} else if (delta < 0 && orig_diff != 0) {
/ 左右の高さが違い、高い方の子の高さが減ったら、高さが減る /
/ 低い方の高さが減る場合は、回転操作が行われるのでここでは扱わない /
return -1;
} else {
/ それ以外では、高さは変わらない /
return 0;
}
} else {
/ 子の高さが変わっていないので、高さは変わらない */
return 0;
}
}
}

void print_tree(const node_t node, int depth) {
int i;
if (node != NULL) {
/ 右の子を出力 (右から出力すると、90度右回転した時にいい感じになる) /
print_tree(node->child[1], depth + 1);
/ このノードを出力 /
for (i = 0; i < depth; i++) printf(" ");
printf("%d (%d)\n", node->data, node->diff);
/ 左の子を出力 */
print_tree(node->child[0], depth + 1);
}
}

void free_tree(node_t *node) {
if (node != NULL) {
free_tree(node->child[0]);
free_tree(node->child[1]);
free(node);
}
}

int main(void) {
node_t root = NULL;
int command, input;
while (scanf("%d", &command) == 1) {
switch (command) {
case 0: / 追加 /
case 3: / 追加して木を出力 /
if (scanf("%d", &input) != 1) break;
printf("add %d\n", input);
modify_tree(&root, input, 1);
if (command == 3) print_tree(root, 0);
break;
case 1: / 削除 /
case 4: / 削除して木を出力 /
if (scanf("%d", &input) != 1) break;
printf("delete %d\n", input);
modify_tree(&root, input, 0);
if (command == 4) print_tree(root, 0);
break;
case 2: / 木を出力 */
printf("print\n");
print_tree(root, 0);
break;
}
}
free_tree(root);
return 0;
}

# 参考サイト

* [AVL Tree by Java -- これで分かったAVL木](http://www.moon.sannet.ne.jp/okahisa/avl-tree/)
* [AVL Tree Visualzation](https://www.cs.usfca.edu/~galles/visualization/AVLtree.html)