はじめに
大学の授業でクイックソートについて習ったので、自分自身の理解を深める目的で、最低限の情報だけ記事にまとめてみました。
操作
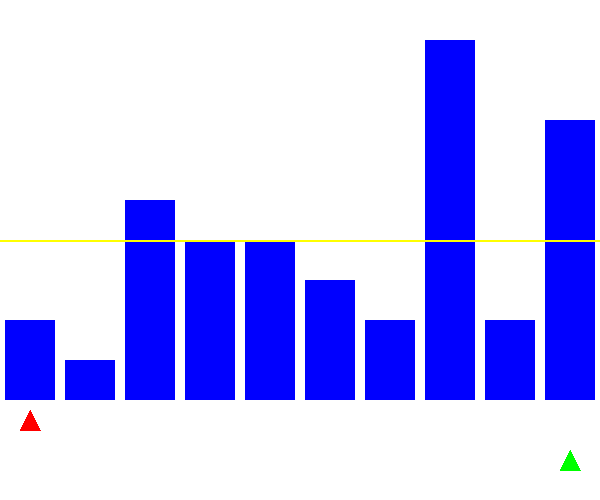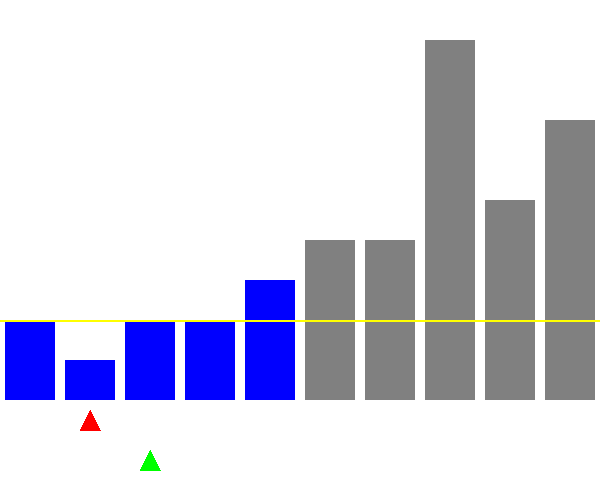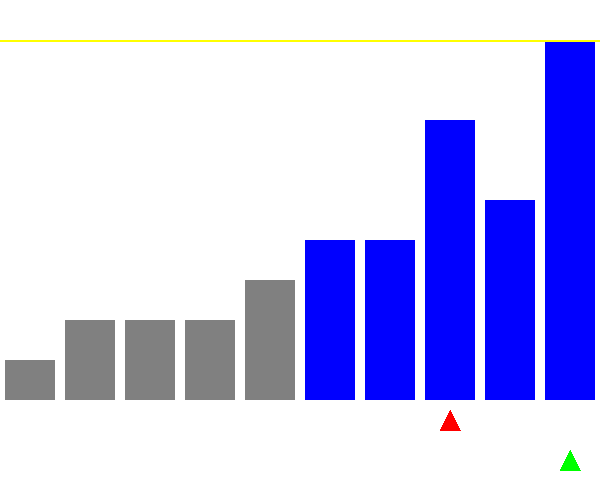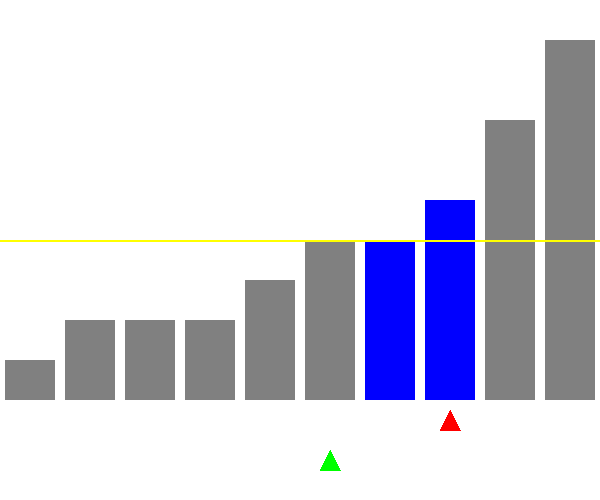
基準値(ピボット)を決めて、その値より小さいグループと大きいグループに分け、それぞれのグループに対して同様の操作を繰り返すことで、ソートを行います。基準値は先頭にする場合など、決め方はいくつかありますが、この記事では配列の中央にしています。
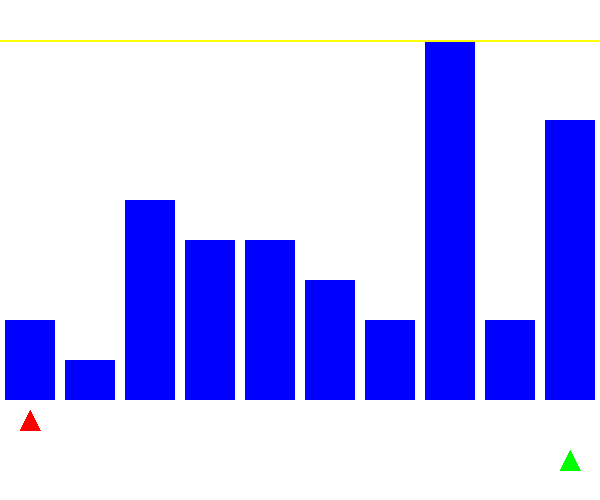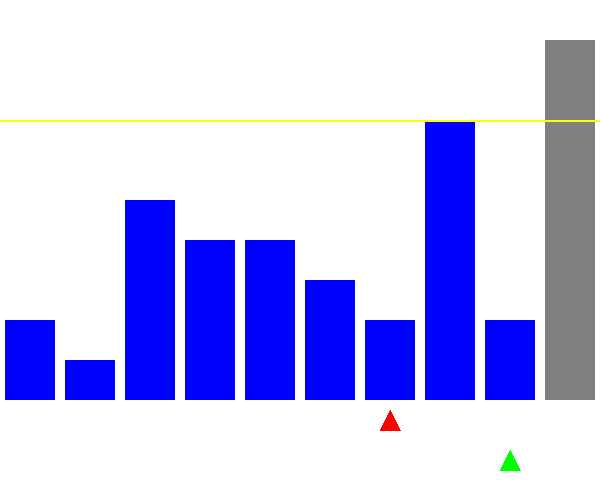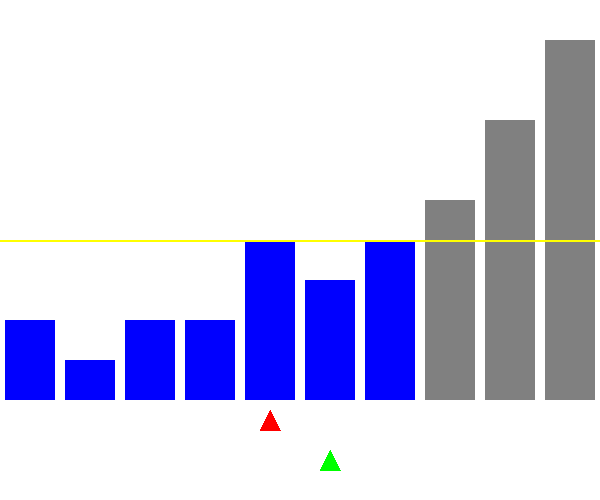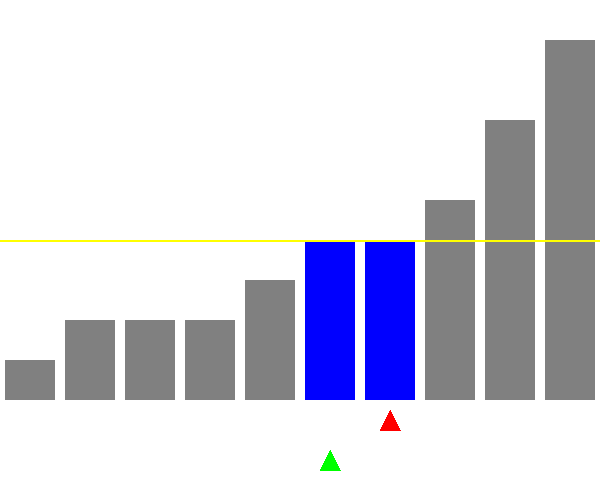
可視化
ピボットの選び方が悪い場合(毎回最大値を選ぶ)
計算量
最悪計算量がO(n^2)で、最良計算量はO(nlogn)です(底はeではなく2)。最悪になるのは、毎回ピボットが最大値か最小値になり、分割が極端に偏るときです。また、最良になるのは、毎回うまく2分割した場合です。
最悪ケース
要素数n~2まで一つずつ減りながらピボットと比較を行うので、n-1~1までの和になります。
$$ 比較回数=(𝑛−1)+(𝑛−2)+⋯+1 = \frac{(𝑛−1)((𝑛−1)+1)}{2} = \frac{𝑛^2−n}{2}=O(n^2) $$
最良ケース
各段階で部分配列ごとに、ピボットと比較していくと考えると、要素数-1が部分配列内での比較回数になります。これに部分配列の数をかければいいので
$$比較回数=(\frac{n}{2^k}-1)×2^k = n-2^k = O(n)$$
と表せます。
何回半分にすれば要素数がnから1になるかを考えればいいので、
$$ 2^x = n$$
となるようなx。つまり定義からlognが分割回数です。したがって、logn回O(n)の計算をするので計算量はO(nlogn)になります。
後述のコードでいうところのleftとrightがpivotの位置で一致する場合は、pivotがその位置に確定するなど、完璧に計算するのが難しかったので、ざっくりとした計算ですが、オーダー自体がざっくりしたものなので、問題ないでしょう。(と思いたい)
平均計算量は、完全ランダムで十分な要素数の配列で考えると、大体二等分に近い形で分割が進むので、最良ケースに近いと考えています。
↓詳しい計算はこちらに載っていました。
安定ソートではない
先頭と末尾からそれぞれ探索し、入れ替えを行うので、同じ大きさの値が頻繁に入れ替わります。したがって安定ソートではありません。
内部ソート
先頭と末尾から条件に合う値を見つけ、それぞれを交換していきますが、後述のコードを見ればわかる通り、入れ替えの操作が配列自身のメモリ領域内で完結できるので、内部ソートです。
コード
pythonで書くと、こんな感じです。
def quick_sort(arr, start, end):
if start >= end:
return
pivot = arr[(start + end) // 2]
left = start
right = end
while left <= right:
while arr[left] < pivot:
left += 1
while arr[right] > pivot:
right -= 1
if left <= right:
arr[left], arr[right] = arr[right], arr[left]
left += 1
right -= 1
quick_sort(arr, start, right)
quick_sort(arr, left, end)
leftとrightが交差した、もしくは重なった時点でwhileを抜けるので、次の部分配列はstart ~ right、left ~ endになります。また、leftとrightが重なった時はその点が基準値と等しいので、left += 1、right += 1をそれぞれ適用することで、その点を除いて部分配列を作成しています。
pythonらしく書くと、こんな感じです。再帰に慣れていない初心者の方は、こちらの方が分かりやすいと思います。
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
left = [i for i in arr if i < pivot]
middle = [i for i in arr if i == pivot]
right = [i for i in arr if i > pivot]
return quick_sort(left) + middle + quick_sort(right)
内包表記でフィルタリングすることで、基準値以上、基準値に等しい、基準値以下に分けています。
この場合、内部ソートではなくなりますが、安定ソートになります。内包表記を使っているため高速に動作しますし、メモリを気にしないなら、こちらの方がいいかもしれません。
総評
強み
- 基本的に高速
弱み
- 安定ソートではない
- かなり限定されるが、遅い時は遅い
→ 特定のパターンに気を付ければ、多くの場面で活用できる。
最後に
ここまで読んで下さりありがとうございました。Pythonだとかなり楽に書ける書き方もありますが、ちゃんと交換で実装するとややこしいです。可視化したことで、コードの目的がはっきりとしてよかったと思います。