はじめに
大学の授業でヒープソートについて習ったので、自分自身の理解を深める目的で、最低限の情報だけ記事にまとめてみました。
そもそもヒープとは
ヒープは、データ構造の一種で、完全二分木とヒープ条件という2つの条件を満たす木構造です。完全二分木とは、すべてのノードが2つの子ノードを持つ、または葉ノードのみを持つ木構造です。ヒープ条件とは、親ノードの値が子ノードの値よりも大きい(最大ヒープ)、または小さい(最小ヒープ)という条件です。
今回は最大ヒープの方を使うので、要するに、枝が二つずつ生えていて、親の方が子より大きい木構造と言えます。
操作
前提として、配列がヒープになっている必要があるため、配列からヒープを作る。その後は以下の1, 2を繰り返す。
- 根が最大値という特性を利用し、末尾と先頭を入れ替えることで、末尾が最大値であることを確定する
- 末尾を除いた部分で、親より子の方が大きい場合は入れ替えることを繰り返し、末尾以外でヒープを再構成する
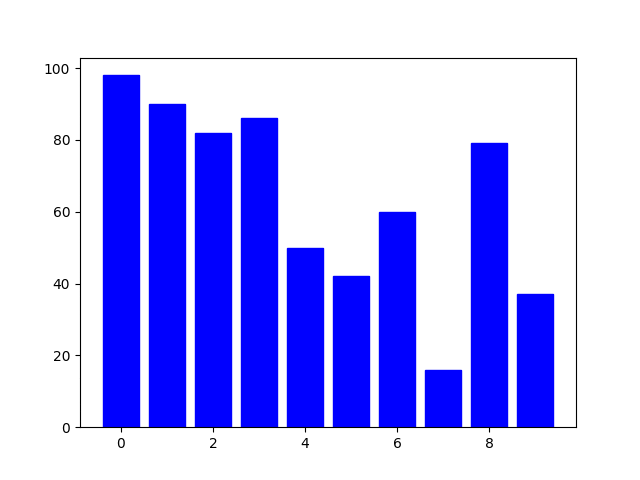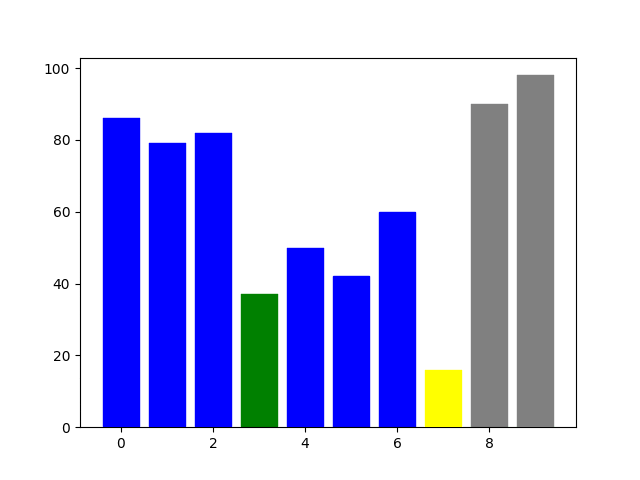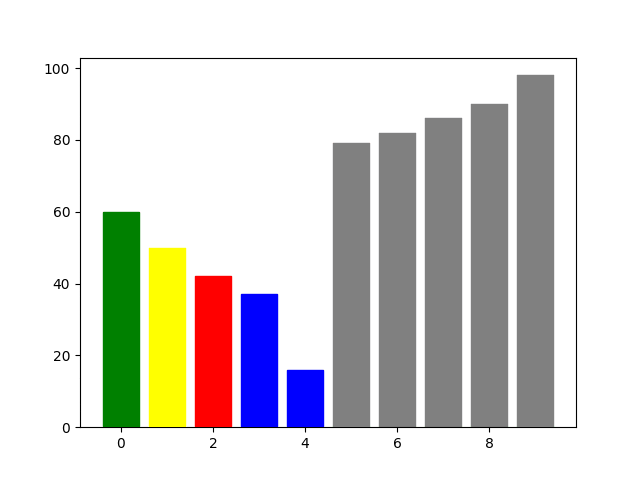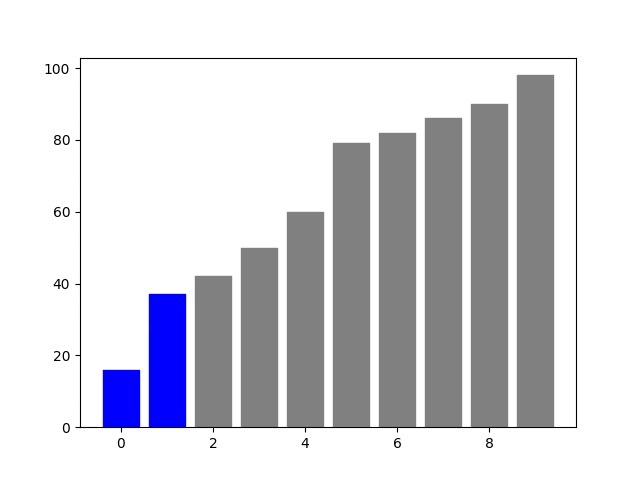
可視化
ヒープ化した後のソート部分を可視化しました。
計算量
根が最大値でない場合、ヒープの深さ分(log n)に比例して交換が発生します。毎回末尾から1つずつ確定していくため、合計n回これを繰り返すことになります。よって、計算量はO(nlog n)です。
安定ソートではない
例として、先頭と末尾の両方が最大値の場合を考えます。先頭と末尾を入れ替え、末尾から確定していく性質上、ソート後の配列では、先頭にあった方の値が末尾に来た状態で最大値が確定されます。このように、順序が入れ替わってしまう場合があるため、安定ソートではありません。
[A3, B2, C1, D3]
[D3, B2, C1, A3] # A3が確定
[B2, C1, D3, A3] # D3が確定
[C1, B2, D3, A3] # 入れ替わってる
内部ソート
親ノードと子ノードの入れ替えも、先頭と末尾の入れ替えも、配列内で完結するため内部ソートです。
コード
pythonで書くと、こんな感じです。
def make_heap(arr):
for i in range(1, len(arr)):
ch = i
while ch > 0:
pa = (ch - 1) // 2
if arr[pa] > arr[ch]:
break
else:
arr[pa], arr[ch] = arr[ch], arr[pa]
ch = pa
def heap_sort(arr):
make_heap(arr)
tail = len(arr) - 1
while tail > 0:
arr[0], arr[tail] = arr[tail], arr[0]
tail -= 1
pa = 0
while True:
lch = pa*2+1
rch = pa*2+2
if lch > tail:
break
elif rch <= tail and arr[rch] > arr[lch]:
tmp = rch
else:
tmp = lch
if arr[pa] >= arr[tmp]:
break
else:
arr[tmp], arr[pa] = arr[pa], arr[tmp]
pa = tmp
交換する候補を右の子と左の子から選んで、親より大きければ入れ替えることを続けているのが内側のwhileです。これを繰り返して、末尾を確定させていき、末尾が先頭まで来たら終了するのが外側のwhileです。
総評
強み
- 安定して高速
- メモリの使用量が少ない
弱み
- 安定ソートではない
→ データ量が多い配列を、高速に処理したい場面で適正あり。
最後に
ここまで読んで下さりありがとうございました。これの前に出したクイックソートとマージソートは再帰ですが、ヒープソートは再帰ではないので、可視化するのがちょっと楽でした。後ろから確定していくのも分かりやすいですしね。