LoginSignup
20
11
@PozihameBaystar

iLQRによる差動二輪車の非線形モデル予測制御

Last updated at Posted at 2023-08-08

はじめに

　練習を兼ねて何度かqiitaにNMPCのMATLABシミュレーションを載せてきましたが、大体C/GMRES関連でした。流石にC/GMRESしか使えないのはプロ野球で言うストガイ感があって寂しいと言いますか、一応制御工学を志す者として心もとないので、他のNMPCシミュレーションを作ってみようと思いました。

そんな中、次のページを見つけました。

微分動的計画法（wikipedia）

思ったよりシンプルで実装しやすそうだったこともあり、引き続き調べたところ、ほぼ同じアルゴリズムのiLQRにたどり着きました。数式的に言うとiLQRは微分動的計画法（以下、DDPとします）からテンソルの縮約項を省略したアルゴリズムです。今回はiLQRのシミュレーションコードを作ります。もし誤りがありましたら、お手数ですがコメントでご指摘頂ければ助かります。

追記

　詳しい理論解説の記事を書いたので、こちらも合わせて読んでいただければと思います。
LQR/iLQRを理解する

環境

MATLAB R2023a

参考文献

　自分が参考にした書籍、記事を提示します。これらを先に読んでいただけるとわかりやすいかと思います。ただし、ベクトルでの微分において自分の記事とは行と列が逆で定義されている文献がありますので注意してください。

数学的準備

　ベクトルの微分について確認します。書籍によっては行と列が逆に定義されている事もあるので注意してください。本記事に載せている説明及びコードは全て以下の定義に基づいて書かれています。

ベクトルでの微分

縦（列）ベクトル

x = [x_{1}, x_{2}, \cdots ,x_{n}]^{T}

に対し、以下の様に定義します（$q$はスカラーです）。

\begin{align}
&\frac{dq}{dx} = \left[\frac{dq}{dx_{1}},\frac{dq}{dx_{2}},\cdots,\frac{dq}{dx_{n}}\right]\\
&\frac{d}{dx}\left(Ax\right)=A \\
&\frac{d}{dx}\left(\frac{1}{2}x^{T}Ax\right)=\frac{1}{2}x^{T}\left(A+A^{T}\right)\\
\end{align}

言葉でまとまると、「縦（列）ベクトルでの微分は横（行）ベクトル」とします。逆に横（行）ベクトルでの微分は縦（列）ベクトルとします。

ベクトルの微分

ベクトルをベクトルで微分する場合、本記事では以下の様に定義します。

\begin{align}
f = [f_{1},f_{2},\cdots,f_{m}]^{T} \\
x = [x_{1}, x_{2}, \cdots ,x_{n}]^{T}\\
\end{align}

\begin{align}
\frac{df}{dx} = 
\begin{pmatrix}
\frac{df_{1}}{dx_{1}} & \frac{df_{1}}{dx_{2}} & \cdots & \frac{df_{1}}{dx_{n}} \\
\vdots & \ddots & & \vdots \\
\frac{df_{m}}{dx_{1}} & \frac{df_{m}}{dx_{2}} & \cdots & \frac{df_{m}}{dx_{n}}
\end{pmatrix}
\end{align}

行列のベクトル微分

行列をベクトルで微分する場合について説明します。
$i,j,k$を順番に行、列、テンソルの枚数とし、

\begin{align}
(A)_{ij} &= a_{ij}\\
x &= [x_{1}, x_{2}, \cdots ,x_{n}]^{T}\\
T &= \frac{dA}{dx}
\end{align}

としたとき、本記事では次のように定義します。

\begin{align}
T_{ijk} = \frac{da_{ij}}{dx_{k}}
\end{align}

ベクトルとテンソルのドット積

ベクトルと3次元テンソル、及びそのドット積

\begin{align}
y &= [y_{1}, y_{2}, \cdots ,y_{n}]\\
(T)_{ijk} &= t_{ijk}\\
A &= y \cdot T
\end{align}

に対し、本記事では以下の様に定義します。

\begin{align}
(A)_{ij} = a_{ij} = \sum_{l}y_{l}\ t_{lji}
\end{align}

言葉にすると、「ドット積の$i$行$j$列はベクトルとテンソル$i$枚目の$j$列の内積」となります。ただし、積の順番が入れ替わるとまた定義も変わるようなので注意してください。

問題設定

　今回は以下のような状態方程式を持つ差動二輪車の運動学モデルを使います。

\begin{align}
&\dot{x} = f(x) = 
\begin{pmatrix}
\frac{R}{2} \cos\theta & \frac{R}{2} \cos\theta \\
\frac{R}{2} \sin\theta & \frac{R}{2} \sin\theta \\
\frac{R}{D} & -\frac{R}{D}
\end{pmatrix}
\begin{pmatrix}
u_{1} \\
u_{2}
\end{pmatrix}\\
&x \triangleq 
\begin{pmatrix}
x\\
y\\
\theta\\
\end{pmatrix}
\end{align}

$R$と$D$は車輪半径と車輪の間の幅です。$u_{1},u_{2}$は右の車輪と左の車輪の角速度であり、これを制御入力とします。

評価関数は次のように設定します。

\begin{align}
J &= (x-x_{ob})^{T} S (x-x_{ob}) + \int_{0}^{T} (x-x_{ob})^{T} Q (x-x_{ob}) + u^{T} R u +B(u) \ d \tau \\
&\fallingdotseq (x-x_{ob})^{T} S (x-x_{ob}) + \sum_{i=0}^{N-1} \left\{ (x_{i}-x_{ob})^{T} Q (x_{i}-x_{ob}) + u_{i}^{T} R u_{i} +B(u_{i}) \right\}\Delta t \\
N \Delta t &= T
\end{align}

つまるところ、座標$x_{ob}$に到達する事を目指す制御をします。$T$は予測ホライズン、$i$は予測ホライズンを離散化、分割した後の各ステップのインデックスです。$B(u)$は入力の制約に関するバリア関数であり、次の様に設定します。

B(u) = -0.15\log(u_{max}-u_{1})(u_{1}-u_{min})-0.15\log(u_{max}-u_{2})(u_{2}-u_{min})

0.15と言うのは実験的に上手く行く係数を求めた結果なので理論的な深い意味はありません。「バリア関数とは？」という方は「最適化　内点法」と調べれば色々説明が出てきますので、そちらを参照してください。

iLQRの理論

　参考文献でも挙げましたが、理論的な内容は

に全て書かれています。ですので、本記事では理解しやすくするための補足に留めておきます。自分なりの理解が入っているので、もし間違いがあればご指摘頂けると助かります。

二次近似による最適化

　DDP及びiLQRで使われている最適化は二次近似による最適化です。それを説明するために、まずは簡単な手法から説明していきます。

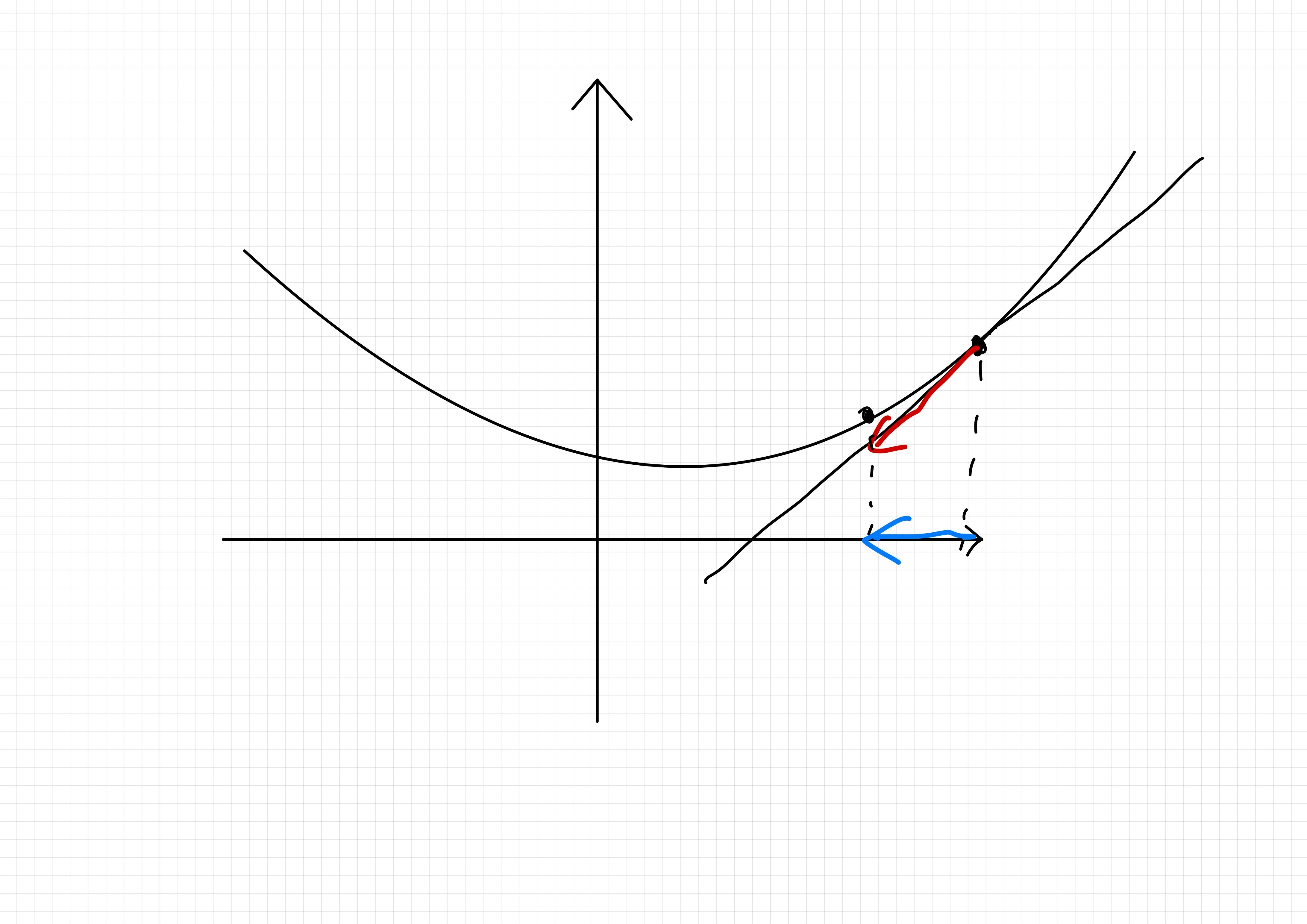
　最も簡単な最適化手法として勾配法と言うのを聞いたことがある方は多いと思います。傾き（微分値）から関数の値が小さくなる方向を求め、その方向に変数をずらしていくという手法です。図にすると次の様になります。

qiita.jpg

つまるところ、現在の変数値付近で関数を直線近似し、その直線を滑り降りる方向に変数値を更新して行くアルゴリズムです。

これに対し、二次近似は現在の変数値付近で関数を二次関数で近似します。その二次関数を滑り降りる方向、つまりその二次関数の頂点方向に変数値を更新して行くアルゴリズムになります。図にすると次の様になります。

qiita2.jpg

どちらも、最適解付近になると更新した変数値が最適解を飛び越えてしまい、関数値が返って大きくなってしまう事があります。この際、「どの程度その方向に変数値をずらすか」を調整し直すのが直線探索です。図で書くと次のようになります。

qiita3.jpg

DDP及びiLQRで使われている最適化はこの二次近似による最適化を多変数に拡張したものです。つまり、ベクトル$x$の関数$h(x)$を最小化するのであれば、

h(x) \approx h(x_{0}) + \frac{d h}{d x}(x_{0})\left(x-x_{0}\right) + \frac{1}{2}\left(x-x_{0}\right)^{T} \frac{d^{2} h}{d x^{2}}(x_{0})\left(x-x_{0}\right)

と二次形式で近似し、この二次形式の近似関数が最小となるポイントへ変数$x$の値を更新して行きます。

ベルマン方程式

　微分動的計画法（wikipedia）を基に説明しますので、先にこのwikiの「動的計画法」の部分までは読んでおいてください。

　最適制御（モデル予測制御）とは、簡単に言えば評価関数を最小となるように制御入力を決定していく制御です。そして（少なくとも評価関数が状態変数$x$と制御入力$u$の関数である限り）状態変数$x$が決まれば、理論上はそこから最適入力解が決定します。つまり、$u$の最適解は$x$から求まるので、予測ホライズン内のあるステップにおける最適な残余コスト（そのステップ以降の分の評価関数の最小値）はそのステップの状態変数$x_{i+1}$のみの関数となります。そこで、現在ステップの入力$u_{i}$を、それらに依存する評価関数（の一部の）値$l(x_{i},u_{i})$と将来の最適な残余コスト値$V(x_{i+1})$の合計が最小になるように調整して行きます。これを制御ホライズン内の最後のステップから最初のステップに向かって繰り返します。これはベルマン方程式を時間軸の後方から解いて行く事に対応します。

アルゴリズム概観

　微分動的計画法（wikipedia）を基に説明しますので、このwikiの「微分動的計画法」と並行して読んでください。

Backward Pass

　上で説明した通り、DDP/iLQRではまず予測ホライズンの後ろのステップから予測ホライズンの初めのステップに向かって$u_{i}$の更新値を求めて行きます。ただし、更新値を求めても直ぐには更新せず（正確には更新できず）、先に予測ホライズンの初めのステップまで更新値を求めてから更新します。

各ステップにおいてwikipediaのページの通り、$l(x_{i},u_{i})+V(x_{i+1})$（の変分）を$x_{i},u_{i}$の関数として二次形式で近似します。しかし、$\delta x$は自由に決定できる値ではなく、$u_{0}$~$u_{i-1}$の更新値（当然まだわからない）によって決定する値です。そこで$\delta x$をパラメータと見なし、$\delta u$を変数として最適解を求めます。直ぐに$u_{i}$を更新できないのは数式からわかる通り$\delta u$の値を求める為に$\delta x$の値が必要となるからです。$\delta x$以外の必要な値（$Q_{x}$や$Q_{u}$）は求まるので、それらを求めます。これを予測ホライズン内の最初のステップまで繰り返します。この一連の繰り返しはBackward Passと呼ばれるようです。尚、$V_{x}$及び$V_{xx}$は計算方法が存在しますが、これは後で説明に出します。

Forward Pass

　全てのステップの$\delta u$が求まったら、次は予測ホライズン内の初めのステップから$u$を更新して行きます。これは次の様なアルゴリズムです。

①$u_{0}(\text{new!})←u_{0}+\delta u_{0}$と$u_{0}$を更新（$\delta x_{0}$は必ず$0$）
②$x_{0}$と$u_{0}(\text{new!})$から$x_{1}(\text{new!})$を計算
③$x_{1}(\text{new!})-x_{1}$から$\delta x_{1}$を計算
④上で求めた$\delta x$を使って$\delta u_{1}$を計算
⑤$u_{1}(\text{new!})←u_{1}+\delta u$と$u_{1}$を更新
⑥$x_{1}(\text{new!})$と$u_{1}(\text{new!})$から$x_{2}(\text{new!})$を計算
（以下$u_{N-1}(\text{new!})$と$x_{N}(\text{new!})$が求まるまで繰り返し）

この一連の繰り返しはForward Passと呼ばれるようです。

まとめ

　Backward Passで更新値決定に必要な値（$Q_{x}$や$Q_{u}$）を求め、Forward Passで更新値を決定して更新して行きます。全体が最適解に収束するまでBackward PassとForward Passを繰り返すと言うのが全体概観になります。AL-iLQR tutorialに全てをまとめた疑似コードが載っていますので、そちらも見て頂ければわかりやすいかと思います（ただし、拡張ラグランジュ法を用いているため一部本記事に無いアルゴリズムが追加されています）。本記事では収束条件も同じくAL-iLQR tutorialで述べられている物を使用します。

コード解説

　上で説明したアルゴリズムをコードにして行きます。以下のコードは主にiLQR tutorial及びAL-iLQR tutorialに基づいています。

構造体

%コントローラーのパラメーター
iLQR.Ts = Ts; %制御周期
iLQR.tf = 1.0; %予測ホライズンの長さ[sec]
iLQR.N = 20; %予測区間の分割数
iLQR.iter = 100; %繰り返し回数の上限値
iLQR.dt = iLQR.tf/iLQR.N; %予測ホライズンの分割幅
iLQR.torelance = 1; %評価関数のズレの許容範囲

% 評価関数中の重み
iLQR.Q = 100 * [1 0 0; 0 1 0; 0 0 0];
iLQR.R = 1*eye(2);
iLQR.S = 100 * [1 0 0; 0 1 0; 0 0 0];

%車のパラメーター
car.R = 0.05; %車輪半径[m]
car.T= 0.2; %車輪と車輪の間の幅(車体の横幅)[m]
car.r = car.R/2; %よく使う値を先に計算
car.rT = car.R/car.T;

% 初期条件
car.x = [0;0;0];
iLQR.u = [0;0];

iLQR.len_x = length(car.x);
iLQR.len_u = length(iLQR.u);

iLQR.U = zeros(iLQR.len_u,iLQR.N);    %コントローラに与える初期操作量

%目標地点
iLQR.x_ob = [3,2,0]';

%拘束条件
iLQR.umax = [15,15];
iLQR.umin = [-15,-15];

以下のコードに登場する構造体及び構造体変数は上のようになっています。

Backward Pass

function [K,d,dV1,dV2] = Backward(X,U,iLQR,car)
    sk = (X(:,end)-iLQR.x_ob)'*iLQR.S; %Vxの初期値
    Sk = iLQR.S; %Vxxの初期値
    Qk = iLQR.Q;
    Rk = iLQR.R;

    K = zeros(iLQR.len_u,iLQR.len_x,iLQR.N);
    d = zeros(iLQR.len_u,iLQR.N);
    dV1 = 0; %dが1次の項を入れる変数
    dV2 = 0; %dが2次の項を入れる変数

    for i = iLQR.N:-1:1
        x = X(:,i);
        u = U(:,i);
        Ak = CalcA(x,u,iLQR.dt,car);
        Bk = CalcB(x,iLQR.dt,car);
        Qx = ((x-iLQR.x_ob)'*Qk)*iLQR.dt + sk*Ak;
        Qxx = Qk*iLQR.dt + Ak'*Sk*Ak;
        dBdu = barrier_du(u,iLQR);
        dBduu = barrier_hes_u(u,iLQR);
        Qu = (u'*Rk)*iLQR.dt + sk*Bk + iLQR.b*dBdu*iLQR.dt;
        Quu = (Rk)*iLQR.dt + Bk'*Sk*Bk + iLQR.b*dBduu*iLQR.dt;
        Qux = Bk'*Sk*Ak;
        K_= -inv(Quu)*Qux; %閉ループゲインの計算
        K(:,:,i) = K_;
        d_ = -inv(Quu)*Qu'; %開ループフィードバックの計算
        d(:,i) = d_;
        sk = Qx + d_'*Quu*K_ + Qu*K_ + d_'*Qux; %Vxの更新
        Sk = Qxx + K_'*Quu*K_ + K_'*Qux + Qux'*K_; %Vxxの更新
        dV1 = dV1 + Qu*d_;
        dV2 = dV2 + (1/2)*d_'*Quu*d_;
    end
end

このコードでは

x_{n+1} = f_{n}(x_{n},u_{n}) \fallingdotseq x_{n} + f(x_{n},u_{n})\Delta t_{s}

と近似しており、

\begin{align}
A_{k} = \frac{\partial f_{k}}{\partial x}\\
B_{k} = \frac{\partial f_{k}}{\partial u}
\end{align}

と定義しています。

$Q_{uu}$行列の正規化はカットしています。

数式の意味的にはwikipediaと同じですが、wikipediaは行と列が自分の定義と逆になっているので一部掛け算の順序が変わっています。

$V_{x}$（コード中sk）及び$V_{xx}$（コード中Sk）はiLQR tutorialの式(12)を使用して更新しています。また、計算途中で$u$の値が制約条件の外に飛び出してしまった時は、バリア関数をReLU関数（微分値は入力値の符号×1）で代用するようにしています。

→バリア関数周辺をアップデートしました。詳しくはモデル予測制御における対数バリア関数の実装をご覧ください。

Forward Pass

function [X,U,J] = Forward(X,U,K,d,dV1,dV2,J,iLQR,car)
    alpha = 1; %直線探索の係数を初期化

    X_ = zeros(iLQR.len_x,iLQR.N+1); %新しいxの値を入れていく変数
    X_(:,1) = X(:,1); %xの初期値は変化しない

    U_ = zeros(iLQR.len_u,iLQR.N); %新しいuの値を入れていく変数
    
    while true
        for i = 1:1:iLQR.N
            U_(:,i) = U(:,i) + K(:,:,i)*(X_(:,i)-X(:,i)) + alpha*d(:,i);
            X_(:,i+1) = func_risan(X_(:,i),U_(:,i),iLQR.dt,car);
        end

        J_new = CalcJ(X_,U_,iLQR);
        dV1_ = alpha*dV1;
        dV2_ = (alpha^2)*dV2;
        z = (J_new-J)/(dV1_+dV2_);

        if 1e-4 <= z && z <= 10 %直線探索が条件を満たしていれば
            J = J_new;
            U = U_;
            X = X_;
            break
        end
       
        alpha = (1/2)*alpha;

    end
end

直線探索の部分についてはAL-iLQR tutorialの式(54)あたりを参照してください。正直なぜこういう条件になるのかよくわかりません。

コントローラー関数

function U = iLQR_control(iLQR,car)
    U = iLQR.U; %前ステップの入力を初期解として使う
    X = Predict(car.x,U,iLQR,car); %状態変数の将来値を入力初期値から予測
    J = CalcJ(X,U,iLQR); %評価関数の初期値を計算
    
    loop = 0;
    while true
        [K,d,dV1,dV2] = Backward(X,U,iLQR,car); %Backward Passの計算
    
        [X,U,J_new] = Forward(X,U,K,d,dV1,dV2,J,iLQR,car); %Forward Passの計算

        loop = loop + 1;

        if abs(J_new-J) <= iLQR.torelance %評価関数値が収束して来たら
            break
        end

        if loop == iLQR.iter %繰り返し回数が限界に来たら
            break 
        end

        J = J_new;
    end
end

入力及び状態変数の初期解として、直前の制御ステップに算出した制御入力の値とそこから予測した状態変数を使用します。

最後に

　早速走らせてみたんですが、自分の環境だと0.6秒くらいで終わります。同じ制御をC/GMRESでやると3.5秒ほどかかったので6倍くらい速い事になりますね。C/GMRESでうんうん唸っていた苦労は何だったのか。。。とりあえずC/GMRES、ニュートン・GMRES、iLQRの3つが使えるようになったのでOKとします。次はSQPかReal-Time-iteration？というやつをやれたら良いかなと思ってます。

追伸
　実はDDPの方のコードも作ってみたのですが、上手く行きませんでした。状態方程式をオイラー積分で離散化したものを解析的に2階微分するのでは$f_{xx}$や$f_{ux}$の精度を保てなかったのではないかと考えています。また上手く行ったら追加で載せようと思います。

全体コード

　コード全体を置いておきます。長いのでgithubにも置いておきます。

close all; clear all; format compact; beep off;%#ok<CLALL> 

Ts = 0.1;  %サンプリング周期[sec]
t_sim_end = 20;   %シミュレーション時間
tsim = 0:Ts:t_sim_end;   %シミュレーションの基準となる時刻

%コントローラーのパラメーター
iLQR.Ts = Ts; %制御周期
iLQR.tf = 1.0; %予測ホライズンの長さ[sec]
iLQR.N = 10; %予測区間の分割数
iLQR.iter = 100; %繰り返し回数の上限値
iLQR.dt = iLQR.tf/iLQR.N; %予測ホライズンの分割幅
iLQR.torelance = 1; %評価関数のズレの許容範囲

% 評価関数中の重み
iLQR.Q = 100 * [1 0 0; 0 1 0; 0 0 0];
iLQR.R = 1*eye(2);
iLQR.S = 100 * [1 0 0; 0 1 0; 0 0 0];

%車のパラメーター
car.R = 0.05; %車輪半径[m]
car.T= 0.2; %車輪と車輪の間の幅(車体の横幅)[m]
car.r = car.R/2; %よく使う値を先に計算
car.rT = car.R/car.T;

% 初期条件
car.x = [0;0;0];
iLQR.u = [0;0];

iLQR.len_x = length(car.x);
iLQR.len_u = length(iLQR.u);

iLQR.U = zeros(iLQR.len_u,iLQR.N);    %コントローラに与える初期操作量

%目標地点
iLQR.x_ob = [3,2,0]';

%拘束条件
iLQR.umax = [15;15];
iLQR.umin = [-15;-15];

%バリア関数用のパラメータ
iLQR.b = 0.3; %バリア関数の重み
iLQR.del_bar = 0.5;
iLQR.bar_C = [eye(iLQR.len_u); -eye(iLQR.len_u)];
iLQR.bar_d = [iLQR.umax; -iLQR.umin];
iLQR.con_dim = length(iLQR.bar_d);

% シミュレーション(ode45)の設定
opts = odeset('RelTol',1e-6,'AbsTol',1e-8);

%臨時追加
X = zeros(iLQR.len_x,iLQR.N+1);
log.X = zeros(iLQR.len_x,iLQR.N+1,401);


tic;
%シミュレーションループ
for i = 1:length(tsim)

    log.u(:,i) = reshape(iLQR.U,[iLQR.len_u*iLQR.N,1]);
    log.x(:,i) = car.x;
    log.X(:,:,i) = X;
    car.x
    
    %シミュレーション計算（最後だけは計算しない）
    if i ~= length(tsim)
        [t,xi] = ode45( @(t,xi) two_wheel_car(t,xi,iLQR.u,car),...
            [tsim(i) tsim(i+1)], car.x, opts);
        %xi = func_risan(car.x,iLQR.u,iLQR.dt,car);
    else
        break
    end
    
    %iLQR法コントローラーを関数として実装
    [U,X] = iLQR_control(iLQR,car);

    iLQR.u = U(:,1);
    iLQR.U = U;
    
    car.x = xi(end,:)';

end
toc;


%
%グラフ化
f=figure();

subplot(5,1,1)
plot(tsim,log.x(1,:),'LineWidth',1); ylabel('x1'); xlabel('Time[s]');
ylim([0,3])
%yticks(0:1:3)
grid on;
set(gca, 'FontSize', 9.5)
subplot(5,1,2);
plot(tsim,log.x(2,:),'LineWidth',1); ylabel('x2'); xlabel('Time[s]');
ylim([0,2])
grid on;
set(gca, 'FontSize', 9.5)
subplot(5,1,3);
plot(tsim,log.x(3,:),'LineWidth',1); ylabel('Φ'); xlabel('Time[s]');
%yticks(0:0.1:0.7)
grid on;
set(gca, 'FontSize', 9.5)
subplot(5,1,4);
plot(tsim,log.u(1,:),'LineWidth',1); ylabel('u1'); xlabel('Time[s]');
%yticks(0:1:11)
grid on;
set(gca, 'FontSize', 9.5)
subplot(5,1,5);
plot(tsim,log.u(2,:),'LineWidth',1); ylabel('u2'); xlabel('Time[s]');
%yticks(0:1:10)
grid on;
set(gca, 'FontSize', 9.5)
%}



%iLQRコントローラー
function [U,X] = iLQR_control(iLQR,car)
    U = iLQR.U; %前ステップの入力を初期解として使う
    X = Predict(car.x,U,iLQR,car); %状態変数の将来値を入力初期値から予測
    J = CalcJ(X,U,iLQR); %評価関数の初期値を計算
    
    loop = 0;
    while true
        [K,d,dV1,dV2] = Backward(X,U,iLQR,car); %Backward Passの計算
    
        [X,U,J_new] = Forward(X,U,K,d,dV1,dV2,J,iLQR,car); %Forward Passの計算

        loop = loop + 1;

        if abs(J_new-J) <= iLQR.torelance %評価関数値が収束して来たら
            break
        end

        if loop == iLQR.iter %繰り返し回数が限界に来たら
            break 
        end

        J = J_new;
    end
end


%状態変数の初期予測関数
function X = Predict(x,U,iLQR,car)
    xk = x;
    xk = func_risan(xk,U(:,1),iLQR.dt,car);
    X = zeros(iLQR.len_x,iLQR.N+1);
    X(:,1) = xk;
    for i = 1:1:iLQR.N
        xk = func_risan(xk,U(:,i),iLQR.dt,car);
        X(:,i+1) = xk;
    end
end


%評価関数の計算
function J = CalcJ(X,U,iLQR)
    %終端コストの計算
    phi = (X(:,end) - iLQR.x_ob)' * iLQR.S * (X(:,end) - iLQR.x_ob);
    
    %途中のコストの計算
    L = 0;
    for i = 1:1:iLQR.N
        bar_val = barrier(U(:,i),iLQR);
        L = L + (X(:,i) - iLQR.x_ob)' * iLQR.Q * (X(:,i) - iLQR.x_ob)...
            + U(:,i)' * iLQR.R * U(:,i)...
            + iLQR.b * bar_val;
    end
    L = L*iLQR.dt; %最後にまとめてdtをかける
    J = phi + L;
end


%Backward Pass
function [K,d,dV1,dV2] = Backward(X,U,iLQR,car)
    sk = (X(:,end)-iLQR.x_ob)'*iLQR.S; %Vxの初期値
    Sk = iLQR.S; %Vxxの初期値
    Qk = iLQR.Q;
    Rk = iLQR.R;

    K = zeros(iLQR.len_u,iLQR.len_x,iLQR.N);
    d = zeros(iLQR.len_u,iLQR.N);
    dV1 = 0; %dが1次の項を入れる変数
    dV2 = 0; %dが2次の項を入れる変数

    for i = iLQR.N:-1:1
        x = X(:,i);
        u = U(:,i);
        Ak = CalcA(x,u,iLQR.dt,car);
        Bk = CalcB(x,iLQR.dt,car);
        Qx = ((x-iLQR.x_ob)'*Qk)*iLQR.dt + sk*Ak;
        Qxx = Qk*iLQR.dt + Ak'*Sk*Ak;
        dBdu = barrier_du(u,iLQR);
        dBduu = barrier_hes_u(u,iLQR);
        Qu = (u'*Rk)*iLQR.dt + sk*Bk + iLQR.b*dBdu*iLQR.dt;
        Quu = (Rk)*iLQR.dt + Bk'*Sk*Bk + iLQR.b*dBduu*iLQR.dt;
        Qux = Bk'*Sk*Ak;
        K_= -inv(Quu)*Qux; %閉ループゲインの計算
        K(:,:,i) = K_;
        d_ = -inv(Quu)*Qu'; %開ループフィードバックの計算
        d(:,i) = d_;
        sk = Qx + d_'*Quu*K_ + Qu*K_ + d_'*Qux; %Vxの更新
        Sk = Qxx + K_'*Quu*K_ + K_'*Qux + Qux'*K_; %Vxxの更新
        dV1 = dV1 + Qu*d_;
        dV2 = dV2 + (1/2)*d_'*Quu*d_;
    end
end


%Forward
function [X,U,J] = Forward(X,U,K,d,dV1,dV2,J,iLQR,car)
    alpha = 1; %直線探索の係数を初期化

    X_ = zeros(iLQR.len_x,iLQR.N+1); %新しいxの値を入れていく変数
    X_(:,1) = X(:,1); %xの初期値は変化しない

    U_ = zeros(iLQR.len_u,iLQR.N); %新しいuの値を入れていく変数

    %直線探索を終わらせるためのカウント
    count = 0;
    %評価関数の最少記録とその周辺
    J_min = J;
    U_min = U;
    X_min = X;
    
    while true
        for i = 1:1:iLQR.N
            U_(:,i) = U(:,i) + K(:,:,i)*(X_(:,i)-X(:,i)) + alpha*d(:,i);
            X_(:,i+1) = func_risan(X_(:,i),U_(:,i),iLQR.dt,car);
        end

        J_new = CalcJ(X_,U_,iLQR);
        dV1_ = alpha*dV1;
        dV2_ = (alpha^2)*dV2;
        z = (J_new-J)/(dV1_+dV2_);

        if 1e-4 <= z && z <= 10 %直線探索が条件を満たしていれば
            J = J_new;
            U = U_;
            X = X_;
            break
        end

        if J_min > J_new %評価関数の最少記録を更新したら
            J_min = J_new;
            U_min = U_;
            X_min = X_;
        end

        if count == 10 %10回やっても直線探索が上手く行かなければ
            J = J_min;
            U = U_min;
            X = X_min;
            break
        end
       
        alpha = (1/2)*alpha;

        count = count + 1;

    end
end


%Akの計算
function Ak = CalcA(x,u,dt,car)
    Ak = eye(3) + ...
        [0 0 -car.r*sin(x(3))*(u(1)+u(2))
        0 0 car.r*cos(x(3))*(u(1)+u(2))
        0 0 0]*dt;
end


%Bkの計算
function Bk = CalcB(x,dt,car)
    cos_ = cos(x(3));
    sin_ = sin(x(3));
    Bk = [car.r*cos_ car.r*cos_
        car.r*sin_ car.r*sin_
        car.rT -car.rT]*dt;
end


%差分駆動型二輪車のモデル(ode用)
function dxi = two_wheel_car(t,xi,u,car)
    dxi = zeros(3,1); %dxiの型を定義
    r = car.r;
    rT = car.rT;
    cos_ = cos(xi(3));
    sin_ = sin(xi(3));
    dxi(1) = r*cos_*u(1) + r*cos_*u(2);
    dxi(2) = r*sin_*u(1) + r*sin_*u(2);
    dxi(3) = rT*u(1) - rT*u(2);
end


%二輪車の離散状態方程式
function xk1 = func_risan(xk,u,dt,car)
    xk1 = zeros(3,1); %xk1の型を定義
    r = car.r;
    rT = car.rT;
    cos_ = cos(xk(3));
    sin_ = sin(xk(3));
    xk1(1) = xk(1) + (r * cos_ * (u(1) + u(2)))*dt;
    xk1(2) = xk(2) + (r * sin_ * (u(1) + u(2)))*dt;
    xk1(3) = xk(3) + (rT * (u(1) - u(2)))*dt;
end


%バリア関数全体
function Bar = barrier(u,control)
    zs = control.bar_d - control.bar_C*u;
    
    Bar = 0;

    %拘束条件の数だけ
    for i = 1:control.con_dim
        Bar = Bar + barrier_z(zs(i),control.del_bar); %値を足していく
    end
end

%バリア関数のu微分（答えは行ベクトルになる）
function dBdu = barrier_du(u,control)
    zs = control.bar_d - control.bar_C*u;

    dBdu = zeros(1,control.len_u);

    for i = 1:control.con_dim
        dBdz = barrier_dz(zs(i),control.del_bar);
        dBdu = dBdu + dBdz*(-control.bar_C(i,:));
    end
end

%バリア関数のuヘッシアン（答えは行列になる）
function dBduu = barrier_hes_u(u,control)
    zs = control.bar_d - control.bar_C*u;

    dBduu = zeros(control.len_u,control.len_u);

    for i = 1:control.con_dim
        dBdzz = barrier_hes_z(zs(i),control.del_bar);
        dBduu = dBduu + control.bar_C(i,:)'*dBdzz*control.bar_C(i,:);
    end
end

%バリア関数（-logか二次関数かを勝手に切り替えてくれる）
function value = barrier_z(z,delta)
    if z > delta
        value = -log(z);
    else
        value = (1/2)*( ((z-2*delta)/delta)^2 -1) - log(delta);
    end
end

%バリア関数の微分値（B(z)のz微分）
function value = barrier_dz(z,delta)
    if z > delta
        value = -(1/z);
    else
        value = (z-2*delta)/delta;
    end
end

%バリア関数のz二階微分（B(z)のz二階微分）
function value = barrier_hes_z(z,delta)
    if z > delta
        value = 1/(z^2);
    else
        value = 1/delta;
    end
end
20
11
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
20
11