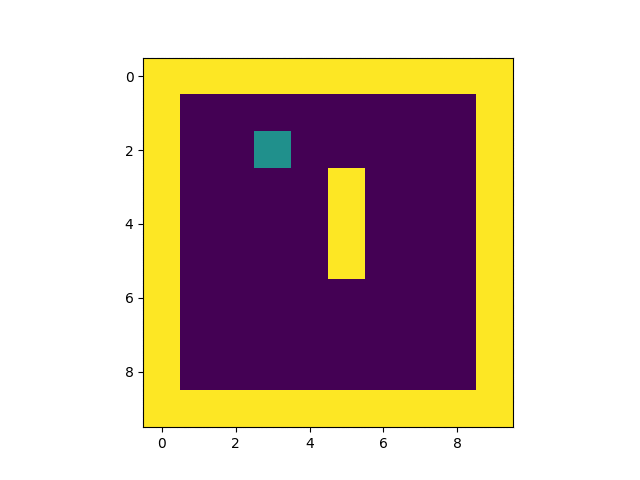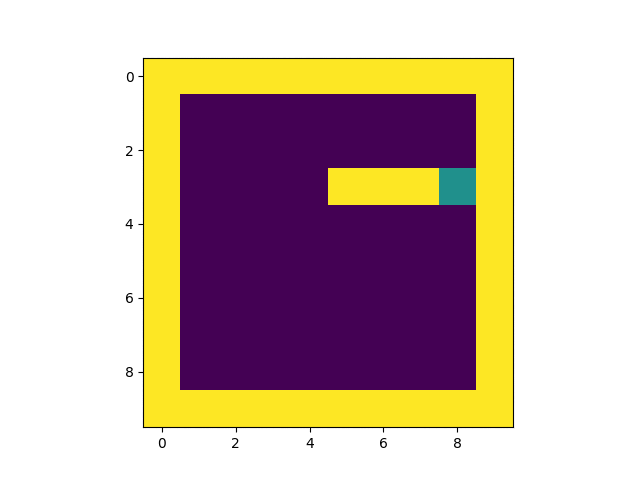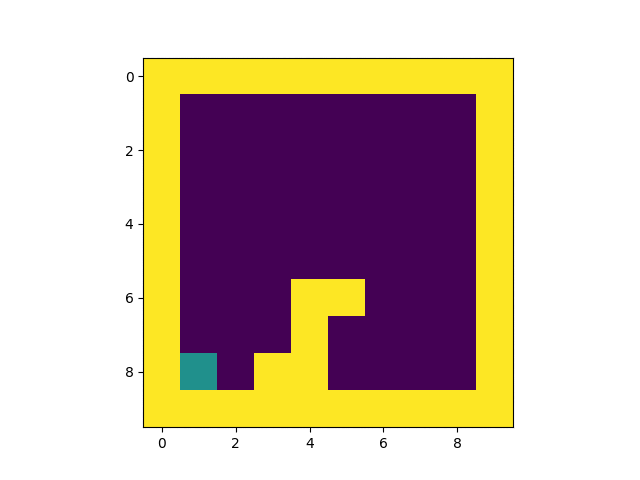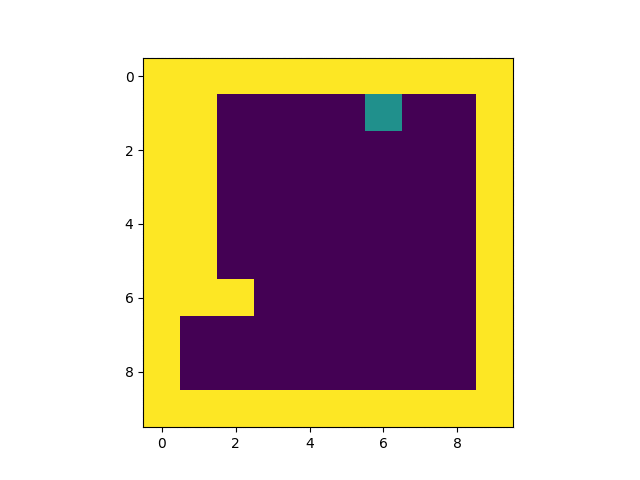
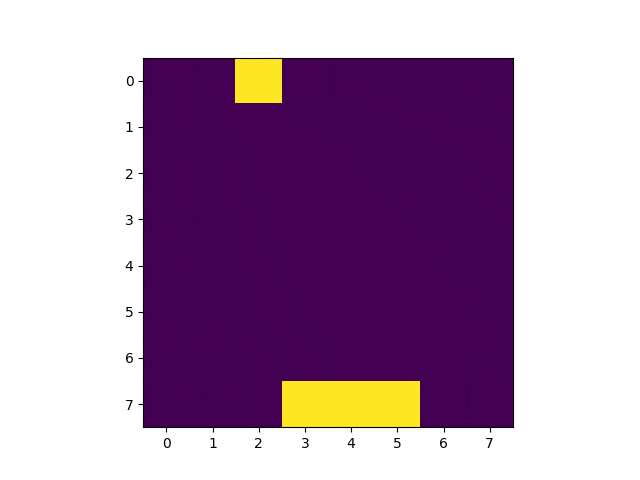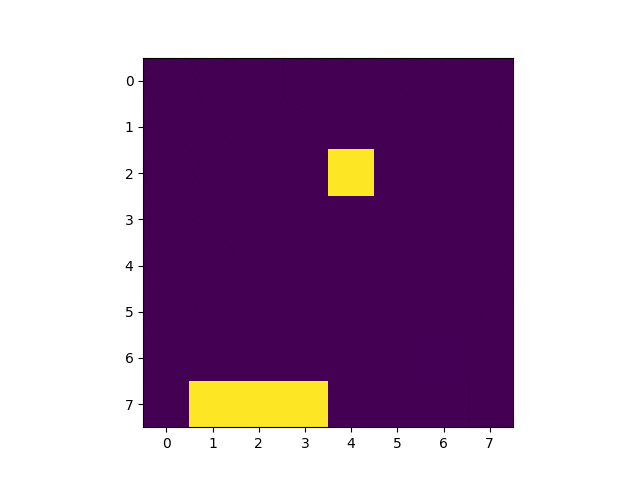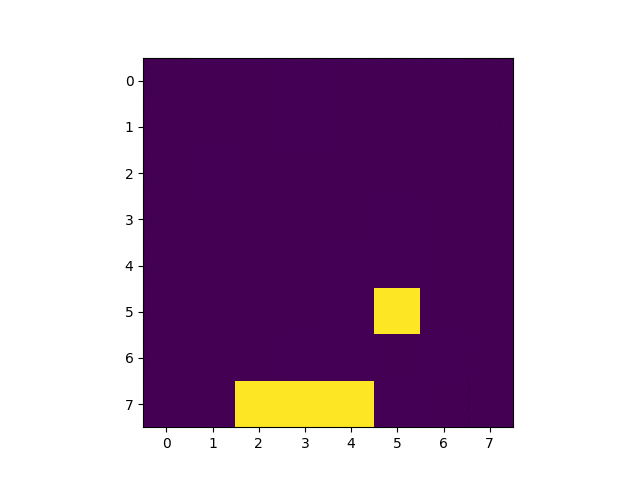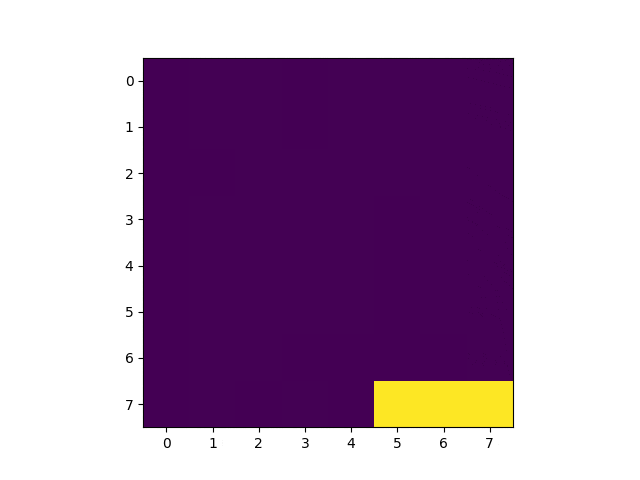KerasでQ学習してみました。今回は畳み込みをしない全結合のニューラル・ネットワークを利用して学習しています。こんな感じ。
Q学習を手軽に試すことの出来るレポジトリが公開されています。
farizrahman4u/qlearning4k - GitHub
こちらを一部改変してみました。ゲームのグリッドサイズを8x8サイズに変更し、学習モデルを保存・再生出来るようにしています。ゲームの実行画面はmatplotlibのアニメーションメソッドを利用して可視化出来るようにしてみました。
サンプルは以下のレポジトリにあります。
train_catch.pyで学習後play_catch.pyで実行することが出来ます。さて、中身をみていきます。
環境
- Python 3.5.2
- tensorflow(0.12.0) GPU
- keras(1.2.1)
Keras2にはアップデートしておらず、バックエンドtensorflowで実行しています。ライブラリがtheano用にChannel firstで書かれていますのでお気をつけ下さい。(バックエンドはそのままですが、スクリプトでChannel firstの指定をしています。)
学習の流れ
8x8のグリッドサイズの画面で、落ちてくる果物をカゴでキャッチするという簡単なゲームです。キャッチ出来れば勝ち、出来なければゲームオーバーです。
冒頭のGIF画像の通り、1000回学習した後、100%キャッチ出来るようになっています。学習の流れは以下の通り。
- ゲーム画面を表示する。
- Kerasを利用してQ値を取得する。
- 保存したモデルのQ値を利用してゲームをさせる。
大まかに分けるとこのようになります。「Q値って何?」ということはさておき、ひとつづつ見ていくことにしましょう。
ゲーム画面を表示する
まずはゲーム画面がどのように表示されているかみてみます。サンプルの/qlearning4k/games/catch.pyとqlearning4k/agent.pyをみていきます。
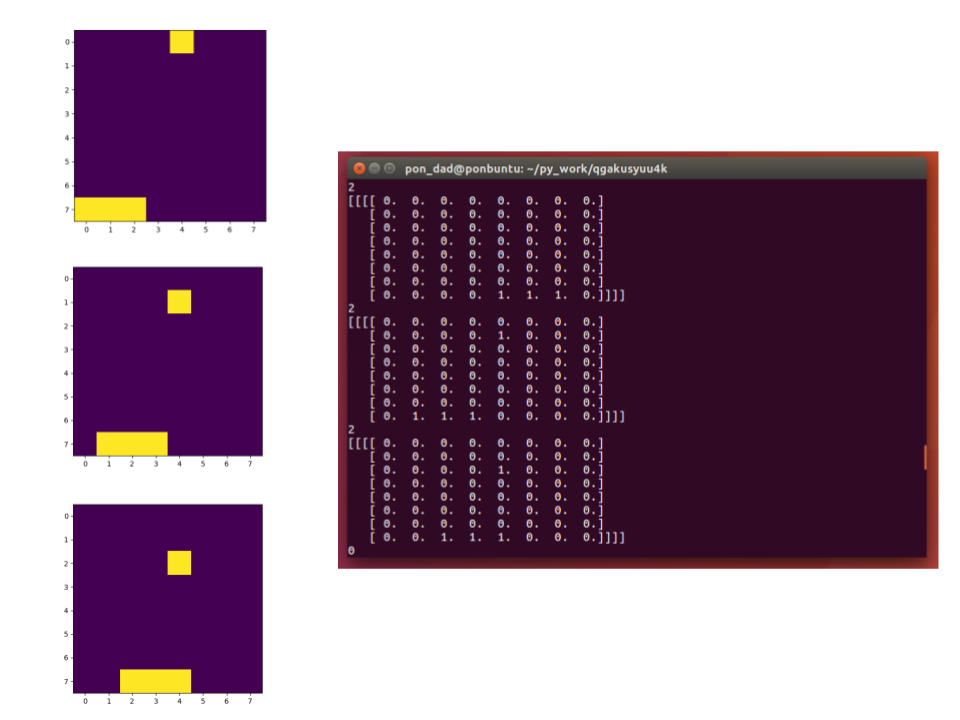
上の画像は学習済みモデルを使って実行したゲーム画面を3コマ切り出したものです。2コマめの配列を覗いてみましょう。
//アクション
2
//ゲーム画面の配列
[[[[ 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 1. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 1. 1. 1. 0. 0. 0. 0.]]]]
ゲーム画面はは8x8の「ゲーム画面の配列」で表現することが出来ます。果物はランダムに落ちてきます。
受け取るカゴのアクションは[左に移動. 移動しない. 右に移動.]の3種類です。右に移動を数値で表すと[0. 0. 1.]となり、上記のように2となります。学習が出来ているので果物の下にしっかりと移動していますね。
さて、ではどうやってこのように「ゲーム画面の配列」から最も良く果物をキャッチ出来る「アクション」をとることが出来るようになったのでしょうか。
ある「状態」の中で「最良のアクション」をとる値をQ値として表すことが出来ます。上の画像で言えば、[左に移動 移動しない 右に移動]のQ値が例えば[0 10 100]であれば、右に移動するはずです。
このQ値をKerasで算出させてみます。
Kerasを利用してQ値を取得する
Q値の算出法を考える
使用させてもらったライブラリのドキュメンテーションではこんな数式が書かれています。
Q(S, a) = r + gamma * Q(S', a')
ちょっとこれだけでは分かりづらいですね。変数を日本語で解説します。
- S 「ゲーム画面の配列」
- a 「アクション」
- S' 「次のゲーム画面の配列」
- a' 「次のアクション」
- r 「報酬」
- gamma 「割引率」
これはQ学習の基本式と同じです。Q学習の解説は以下サイトのサンプルコードが分かりやすかったです。
Q学習で最良経路をPythonで求めてみる - The jonki
得られた報酬から遡ることで、「最良のアクション」をとる値(Q値)が得られます。ここでは果物をキャッチして「報酬」を得た場合(最初はランダムに移動させます)、そこに至るまでの行動のQ値を算出します。
さて、ライブラリのドキュメンテーションにもうひとつこんな式が書かれています。
a' = argmax(M(S'))
変数Mは以下の通り、
- M 「ニューラルネットワークモデル」
ですので、「ニューラルネットワークモデル」に「次のゲーム画面の配列」を代入した最大値が、「次のアクション」となります。
試しに右に移動した時の戻り値を見てみると[[-0.24830072 0.02182534 0.98698837]]こんな配列になっています。argmax()で得られる値は3番目なので右に移動するという訳です。
クール!
Kerasを利用する
ここでようやくKerasの説明に入ります。train_catch.pyはこの様に書かれています。
from keras import backend as K
K.set_image_dim_ordering("th")
assert K.image_dim_ordering() == "th"
from keras.models import Sequential
from keras.layers import Flatten, Dense
from qlearning4k.games import Catch
from keras.optimizers import *
from keras.utils import np_utils
from qlearning4k import Agent
grid_size = 8
hidden_size = 64
nb_frames = 1
model = Sequential()
model.add(Flatten(input_shape=(nb_frames, grid_size, grid_size)))
model.add(Dense(hidden_size, activation='relu'))
model.add(Dense(hidden_size, activation='relu'))
model.add(Dense(3))
model.compile(sgd(lr=.2), "mse")
catch = Catch(grid_size)
agent = Agent(model=model)
agent.train(catch, batch_size=10, nb_epoch=1000, epsilon=.1)
model.save_weights('catch.h5');
冒頭に書いたようにtheano用にChannel firstで書いています。今回は全結合のニューラルネットワークで、ゲーム画面8x8を隠れ層64次元に並列化し、[左 移動しない 右]の3次元に出力します。
今回は1000エポック訓練したデータをcatch.h5に保存し、実行時に読み込むようにしました。
qlearning4k/agent.pyの実行部分def play()以降に以下の様に記述されています。
q = model.predict(S)[0]
possible_actions = game.get_possible_actions()
q = [q[i] for i in possible_actions]
action = possible_actions[np.argmax(q)]
上で解説した式と同じですね。
Q学習の工夫
さて、もう少しです。通常の機械学習と異なり、Q学習(強化学習)では、正解ラベルがない為、学習にひと工夫必要になります。
「報酬」から遡って「ゲーム画面の配列」を取得しなければなりません。
そこで、「報酬」を得た「ゲーム画面の配列」のみを抽出して学習させる必要があります。具体的にはエポック毎のフレームをメモリに保存しておき、「報酬」を得たフレームのみ学習に使います。(qlearning4k/agent.py のdef train()部分)
ここでは8つの「ゲーム画面の配列」が得られ、8つめの配列で「報酬」1が得られています。「割引率」はgamma=0.9で指定しています。
上述の計算式をまとめてみてみます。
Q(S, a) = r + gamma * Q(S', argmax(M(S')))
この計算式にwhileループを利用して代入していきます。
保存したモデルのQ値を利用してゲームをさせる
利用したライブラリは実行結果のフレームを画像で保存するのですが、学習した感が欲しかったので、アニメーションで表示させてみました。
qlearning4k/agent.pyのdef play()を少し書き換えました。
fig = plt.figure()
if visualize:
ims = []
for i in range(len(frames)):
im = plt.imshow(frames[i], interpolation='none', animated=True)
ims.append([im])
ani = animation.ArtistAnimation(fig, ims, interval=50, blit=True, repeat_delay=1000)
plt.show()
matplotlibのアニメーションメソッドを利用しました。
※豆知識…Macで実行する際はanimation.ArtistAnimationのパラメータをblit=Falseにしないとエラーになります。
まとめ
ライブラリがとてもシンプルに記述してあったので、ドキュメンテーションに沿って記述したところ上手く学習させることが出来ました。
もう少し複雑なモデルを学習させる際は、畳込み層を利用したサンプルもあります。
これは懐かしのスネークゲームを畳み込みニューラルネットワークで10,000エポック学習させたものです。うねうねしてて見てて飽きませんね。
では。