1. 概要

前回まででMDの基礎はさらったと思うので、規模を大きくしていきましょう。
同時進行でコードも再利用性、保守性の高いものに変えていきます。

2. クラス化

分子(原子)に紐づいている情報は多いので、まずは分子（原子）のクラスを作りましょう。
とりあえず単原子分子だけ考えるのでAtomというクラス名にしましょう。
大きさのある分子を扱うのは剛体の力学を考えなければならず非常に難易度が高いです。挫折した経験があります。

class Atom:
    def __init__(self, kind, r, v):
        self.kind = kind
        self.r = r
        self.r_before = r
        self.v_half_after = np.array([0.0, 0.0, 0.0])
        self.v_half_before = v
        self.f = np.array([0.0, 0.0, 0.0])
        self.m = LJ_params[kind][2]

    def clear_force(self):
        self.f = np.array([0.0, 0.0, 0.0])

    def update_position(self, initial=False):
        a = self.f / self.m
        if initial:
            self.v_half_after = self.v_half_before + 0.5 * a * dt
        else:
            self.v_half_after = self.v_half_before + a * dt
        self.r = self.r_before + self.v_half_after * dt
        # 値の更新
        self.v_half_before = self.v_half_after
        self.r_before = self.r

必要な関数は2つです。

clear_force: 名前の通り、力をリセットします。複数の分子間で力を計算する際関さんが必要なため、事前にリセットしておきます。
update_position: 名前の通り、位置を更新します。速度もちゃっかり更新してます。initialがTrueの時は前回解説したようにEuler法で更新を行います。

力の更新には他の分子の情報が必要です。外部の関数で計算してあげます。

def calc_force(a1: Atom, a2:Atom) -> np.ndarray:
    disp = a2.r - a1.r
    abs_r = np.linalg.norm(disp)
    C = LJ_pair_params[a1.kind][a2.kind]['C']
    D = LJ_pair_params[a1.kind][a2.kind]['D']
    return (C / abs_r ** 14 - D / abs_r ** 8) * disp

dispはdisplacementの略です。abs_rは分子間距離です。
今回からちゃっかりベクトルにしているので、マイナーチェンジが行われています。

\begin{align}
\boldsymbol{F}(\boldsymbol{r})&=\left(\frac{C}{|\boldsymbol{r}|^{13}}-\frac{D}{|\boldsymbol{r}|^{7}}\right)\frac{\boldsymbol{r}}{|\boldsymbol{r}|}\\
&=\left(\frac{C}{|\boldsymbol{r}|^{14}}-\frac{D}{|\boldsymbol{r}|^{8}}\right)\boldsymbol{r}
\end{align}

という簡略化です。冪乗でnp.powerの方が早いんでしょうか。検討しておきましょう。
検討した記事はこちらhttps://qiita.com/PlusF/items/83bf1a1be6a82452d780

3. パラメータの設定

前節でLJ_paramsだとかLJ_pair_paramsだとかが出てきていました。こいつらの説明を加えておきます。

dt = 1e-15

NA = 6.022e23  # アボガドロ数

LJ_params = {
    # epsilon, sigma, m
    'Ar': [1.67e-21, 3.40e-10, 39.948 / NA * 1e-3]
}

LJ_pair_params = {}

def set_params():
    for kind_1, (eps_1, sigma_1, _) in LJ_params.items():
        params_tmp = {}
        for kind_2, (eps_2, sigma_2, _) in LJ_params.items():
            eps = np.sqrt(eps_1 * eps_2)
            sigma = (sigma_1 + sigma_2) / 2
            params_tmp[kind_2] = {
                'A': 4 * eps * sigma ** 12,
                'B': 4 * eps * sigma ** 6,
                'C': 48 * eps * sigma ** 12,
                'D': 24 * eps * sigma ** 6
            }
        LJ_pair_params[kind_1] = params_tmp

LJ_paramsには辞書型で$\varepsilon$, $\sigma$, $m$が格納されています。これらは原子ごとの値です。LJ_pair_paramsには、ポテンシャルや力の計算で必要になる係数を計算して格納してあります。LJ_paramsに値を入れるだけで原子の種類を容易に増やすことができます。

4. `do_step`

ステップ一回の計算を行うdo_step関数を紹介します。

def do_step(atom_list, initial=False):
    for a in atom_list:
        a.clear_force()

    for i in range(len(atom_list)):
        a1 = atom_list[i]
        for j in range(i+1, len(atom_list)):
            a2 = atom_list[j]
            f = calc_force(a1, a2)
            a1.f -= f
            a2.f += f

    for a in atom_list:
        a.update_position(initial=initial)

力をリセットする
各原子間で力を計算する
力をもとに速度、位置の更新を行う

5. `main`

set_paramsの呼び出しを忘れないようにしましょう。
これで簡単に10000ステップのシミュレーションを行えました。

def main():
    set_params()
    a1 = Atom('Ar', np.array([0, 0, 0]), np.array([0, 0, 0]))
    a2 = Atom('Ar', np.array([5e-10, 0, 0]), np.array([0, 0, 0]))

    atom_list = [a1, a2]
    do_step(atom_list, initial=True)
    for _ in range(10000):
        do_step(atom_list)

エネルギーの保存を確認しておきましょう。

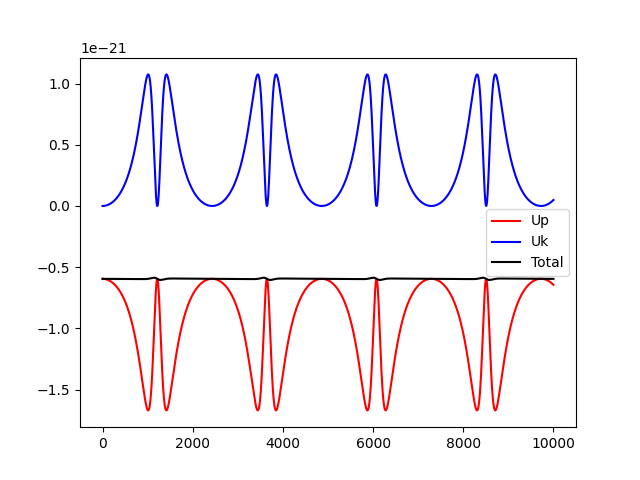
多少ブレがありますが、まあ良いでしょう。

-1. 次回予告

次回はさらに原子を増やしていきます。
リンクはこちらhttps://qiita.com/PlusF/items/64b7c8ecd81584a81f62
前回はこちらhttps://qiita.com/PlusF/items/22ed49534b6fc6be174c

PythonでMDことはじめ vol. 4