概要
皆さんカーボンナノチューブ(carbon nanotube, CNT)という物質はご存じでしょうか.
いろいろすごい物質です.
今回はカーボンナノチューブの大きな特徴である,ファンホーブ特異点(van Hove singularity)を持つ電子状態密度(density of state, DOS)を計算し描画していきます.
理論
前回の記事でグラフェンのエネルギーバンドを計算し描画しました.それを使ってDOSを計算するのでまだ読んでいない方はぜひ.
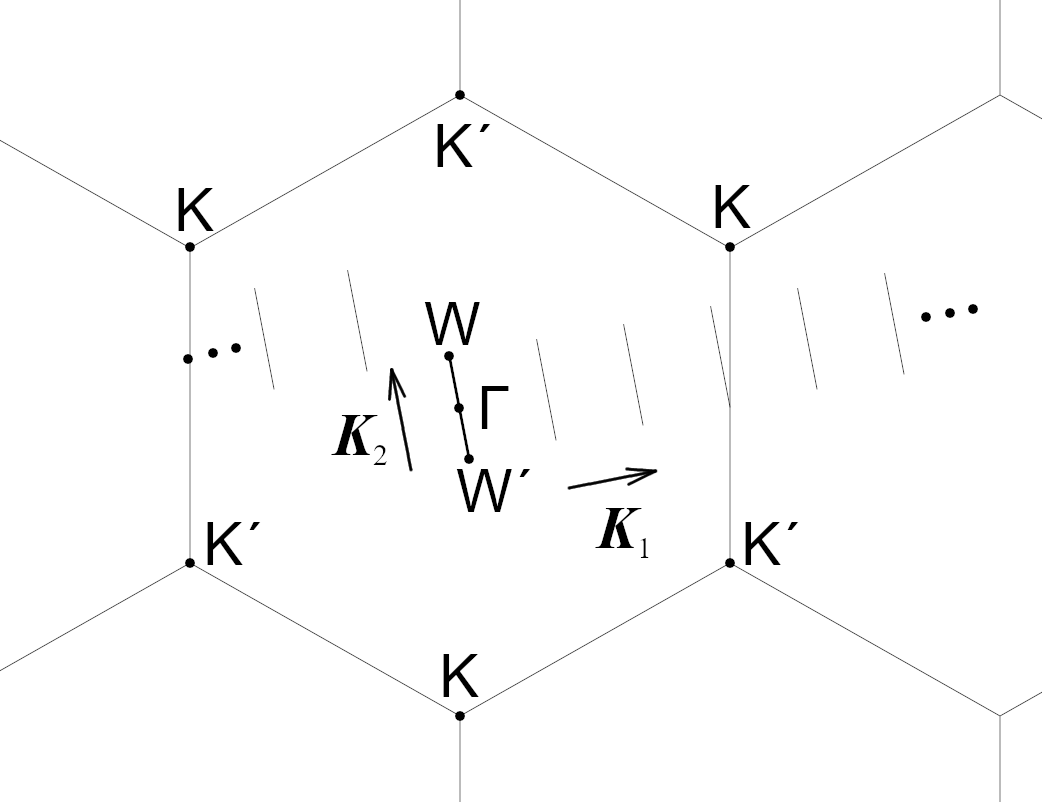
コンテキストを端折ってしまいますが,単層CNTの電子の波動関数がとりうる波数ベクトルは限られており,カッティングラインと呼ばれる線分上のみとなる.単層CNTの分散関係は,グラフェンの分散関係に量子条件を入れることで次のように求まる.
E_{\mu}(k)=E_{2g}\left(k\frac{\vec{K_2}}{|\vec{K_2}|}+\mu \vec{K_1}\right), \left(-\frac{\pi}{|\vec{T}|}<k<\frac{\pi}{|\vec{T}|}, \mu=0,1,...,N-1\right)
ただし$\vec{K_1}$,$\vec{K_2}$は単層CNTの単位胞に対応する逆格子ベクトルであり,$\vec{T}$は実空間上の並進ベクトル,$N$は単位胞中の六角形の数である.
一般に,エネルギー$\epsilon$における状態密度は,デルタ関数の和であらわされる.
D(\epsilon)=\frac{1}{V}\sum_{\vec{k}}{\delta(\epsilon-E(\vec{k}))}
このとき,$V$は系の体積であり,取りうるすべての波数$\vec{k}$の和を考える.単層CNTの電子状態密度は,波数が量子化されることから,以下のようになる.
D(\epsilon)=\frac{1}{2\pi}\int_{-\frac{\pi}{|\vec{T}|}}^{\frac{\pi}{|\vec{T}|}}\sum_{\mu=0}^{N-1}{\delta(\epsilon-E_\mu(k))\mathrm{d}k}
(かなり端折っています)
コード
さて,ようやく準備が整いました.今回はデルタ関数や積分があるので骨が折れます.
(scipyなんかで積分ってできるのかしら.TODOですね.)
まずはデルタ関数から.ガウス関数で近似します.
def delta(x, n_delta=10000): # ガウス関数で近似. nを大きくするほどデルタ関数に近づく
ret = np.exp(-1 * n_delta * x ** 2)
return np.sqrt(n_delta / np.pi) * ret
定数が多いのでクラスにします.BandOfGrapheneクラスは前回の記事参照.
import numpy as np
class DOSOfCNT:
a = 2.46
a1 = np.array([np.sqrt(3) / 2, 1 / 2]) * a
a2 = np.array([np.sqrt(3) / 2, - 1 / 2]) * a
def __init__(self, n: int, m: int):
self.n = n
self.m = m
# カイラルベクトル
self.Ch = n * self.a1 + m * self.a2
self.L = np.linalg.norm(self.Ch)
# 直径
self.d_tube = self.L / np.pi
gcd = np.gcd(2 * m + n, 2 * n + m)
self.t1 = (2 * m + n) / gcd
self.t2 = -1 * (2 * n + m) / gcd
# 並進ベクトル
self.T = self.t1 * self.a1 + self.t2 * self.a2
# 単位胞内の六角形の数
self.N = int(2 * (n ** 2 + m ** 2 + n * m) / gcd)
# 逆格子ベクトル
self.b1 = np.array([1 / np.sqrt(3), 1]) * 2 * np.pi / self.a
self.b2 = np.array([1 / np.sqrt(3), -1]) * 2 * np.pi / self.a
self.K1 = 1 / self.N * (- self.t2 * self.b1 + self.t1 * self.b2)
self.K2 = 1 / self.N * (m * self.b1 - n * self.b2)
# 積分の範囲
k_min = -1 * np.pi / np.linalg.norm(self.T)
k_max = np.pi / np.linalg.norm(self.T)
self.dk = 1 / 1000
self.k_range = np.linspace(k_min, k_max, int(1 / self.dk))
self.band_of_graphene = BandOfGraphene()
self.band_of_graphene.s = 0 # 結合性バンド,半結合性バンドが対称になる
積分の分割数なんかもここで指定しちゃっています.少ないと妙なピークが出てきたり,多すぎると時間がかかったり,ここは調整してください.
では本題の計算をクラス関数として実装します.時間がかかるのでtqdmを使って進捗表示しています.
def E_mu(self, k, mu, sign): # グラフェンのエネルギー分散関係に,CNTの量子化条件を入れる
x, y = k * self.K2 / np.linalg.norm(self.K2) + mu * self.K1
return self.band_of_graphene.E_2g(x, y, sign)
def DOS(self, E):
ret = 0
for k in tqdm(self.k_range):
for mu in range(1, self.N + 1):
ret += self.dk * (delta(E - self.E_mu(k, mu, '+')) + delta(E - self.E_mu(k, mu, '-'))) # 結合性バンドと反結合性バンドのDOSの和
return ret / (2 * np.pi) / 2
描画!
いい感じに描画します.
def plot(self, E_range: tuple):
plt.figure(figsize=(8, 10))
E = np.linspace(*E_range, 1000)
plt.plot(E, self.DOS(E), color='k')
plt.xlabel('Energy [eV]')
plt.ylabel('DOS')
plt.xlim(*E_range)
plt.ylim(0, )
plt.xticks(range(E_range[0], E_range[1] + 1))
plt.yticks([0])
plt.show()
結果
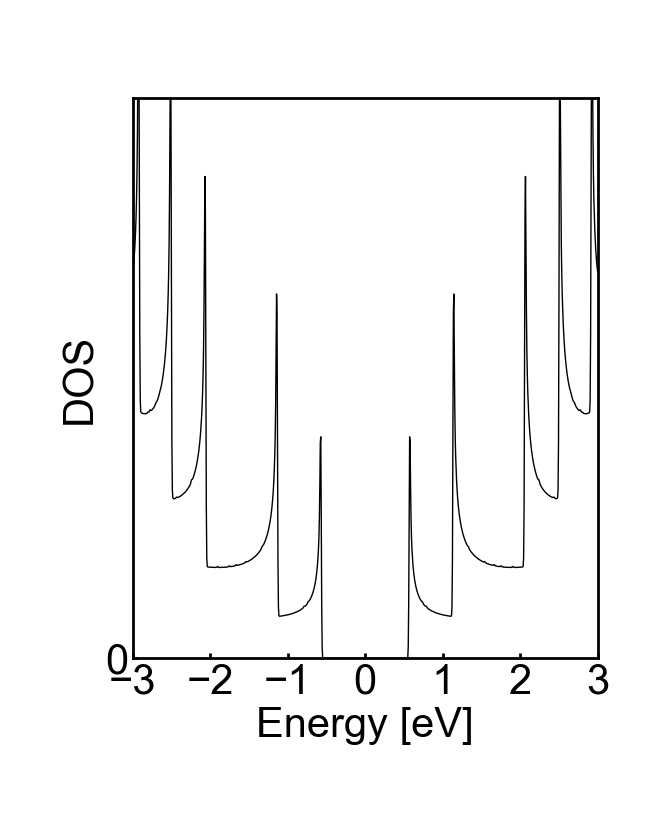
カイラリティ(6, 5)の場合はこんな感じ.発散している点がファンホーブ特異点です.
備考
GitHubにてコードを公開中.