オートエンコーダー
概要
オートエンコーダーは、入力画像を圧縮し復元するモデルです。
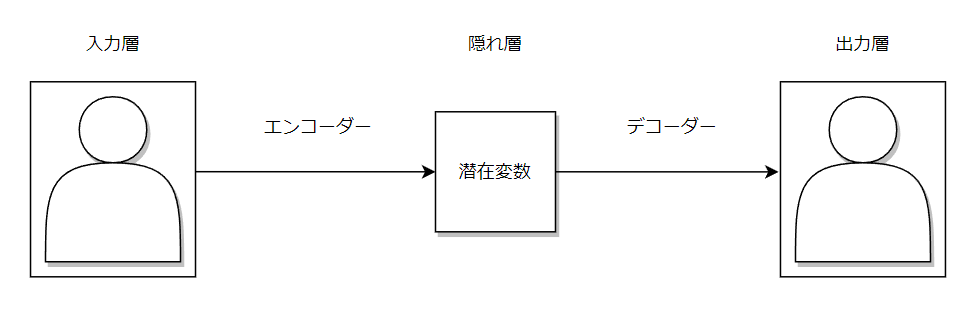
入力層、隠れ層、出力層の三層構造となっています。
入力層から隠れ層はエンコーダーといい入力画像を低次元データに圧縮します
隠れ層から出力層はデコーダーといい低次元データを入力画像と同じになるように拡張します。
つまりエンコーダーによってデータの要約を行い、デコーダーによって要約されたデータをもとに復元を行います。
この要約されたデータのことを潜在変数といいます。
使用場面
- 異常検知
- ノイズ除去
- ニューラルネットワーク学習時に使用(※現時点で使用されることはほぼない)
モデル構造
class Autoencoder(nn.Module):
def __init__(self):
super().__init__()
self.encoder = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(True))
self.decoder = nn.Sequential(
nn.Linear(200, 784),
nn.Sigmoid())
def forward(self, image):
x = self.encoder(image)
x = self.decoder(x)
return x
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Linear-1 [-1, 1, 200] 157,000
ReLU-2 [-1, 1, 200] 0
Linear-3 [-1, 1, 784] 157,584
Sigmoid-4 [-1, 1, 784] 0
================================================================
Total params: 314,584
Trainable params: 314,584
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.02
Params size (MB): 1.20
Estimated Total Size (MB): 1.22
----------------------------------------------------------------
構築時の注意点
- 入力サイズと出力サイズを同サイズにすること
- 入力画像は正規化を行い0~1の範囲に収まるようにする
- 活性化関数は以下の通り
- エンコーダーの後にReLU関数
- デコーダーの後にSigmoid関数
損失関数
誤差関数として以下のような再構成誤差を使用します。
数式としてはバイナリークロスエントロピー誤差とほぼ同じになります
$ H(p,q) =- \sum^{N}_{i=1}p_i log q_i = -ylogy'-(1-y)log(1-y') $
学習
criterion = nn.BCELoss()
optimizer = optimizers.Adam(autoencoder.parameters())
autoencoder.train()
for epoch in range(epoch_num):
for x,_ in dataloader:
x = input.to(device)
preds = autoencoder(x)
loss = criterion(preds, x)
optimizer.zero_grad()
loss.backward()
optimizer.step()
変分オートエンコーダー
概要
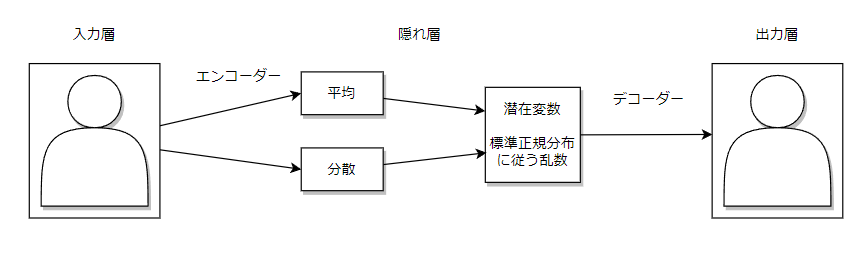
変分オートエンコーダーはオートエンコーダーにおける、デコーダーを生成モデルとして使用するモデルのことです。
オートエンコーダーとの相違点として潜在変数を標準正規分布に従うように標準化する点が異なります。
以下のように潜在変数に対して標準化を行い、潜在変数を標準正規分布に従うように変換させます。
使用場面
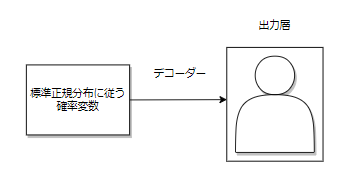
- 生成モデルとして使用する場合にはデコーダーの部分のみを使用します。
入力としては標準正規分布に従う確率変数を入力として、データを出力します。
モデル構造
# エンコーダ
class Encoder(nn.Module):
def __init__(self, device='cpu'):
super().__init__()
self.device = device
self.fc = nn.Linear(784, 200)
self.fc_mean = nn.Linear(200, 10)
self.fc_var = nn.Linear(200, 10)
def forward(self, x):
x = self.fc(x)
x = torch.relu(x)
mean = self.fc_mean(x)
var = self.fc_var(x)
var = F.softplus(var)
return mean, var
# デコーダ
class Decoder(nn.Module):
def __init__(self, device='cpu'):
super().__init__()
self.device = device
self.linear1 = nn.Linear(10, 200)
self.linear2 = nn.Linear(200, 784)
def forward(self, x):
x = self.linear1(x)
x = torch.relu(x)
x = self.linear2(x)
x = torch.sigmoid(x)
return x
# 変分オートエンコーダー
class VAE(nn.Module):
def __init__(self, device='cpu'):
super().__init__()
self.device = device
self.BCE_criterion = nn.BCELoss()
self.encoder = Encoder(device=device)
self.decoder = Decoder(device=device)
def forward(self, x):
mean, var = self.encoder(x)
z = self.reparametrizaion(mean, var)
y = self.decoder(z)
return y, z
# 平均と分散をもとに標準正規分布に従う潜在変数を出力
def reparametrizaion(self, mean, var):
eps = torch.randn(mean.size()).to(self.device)
z = mean + torch.sqrt(var) * eps
return z
# 誤差
def lower_bound(self, x):
mean, var = self.encoder(x)
z = self.reparameterize(mean, var)
y = self.decoder(z)
# 再構成誤差
reconst = self.BCE_criterion(y, x)
# 正則化損失
kl = - 1/2 * torch.mean(torch.sum(1 + torch.log(var) - mean**2 - var, dim=1))
loss = reconst + kl
return loss
損失関数
誤差関数として以下のような再構成誤差とKLダイバージェンスを使用します。
1. 再構成誤差
$ H(p,q) =- \sum^{N}_{i=1}p_i log q_i = -ylogy'-(1-y)log(1-y') $
2. KLダイバージェンス
$ reg = - \frac{1}{2} \sum^{N}_{i=1} (1 + log_i^2 - μ_j^2 - σ_j^2) $
最小にするためには、平均(μ)が0で分散(σ)が1の時に最小化します。
つまり標準正規分布に従うときです
3. 損失関数
再構成誤差とKLダイバージェンスを足し合わせたものが、変分オートエンコーダの損失関数となります
損失関数 = 再構成誤差 + KLダイバージェンス
学習
criterion = vae.lower_bound
optimizer = optimizers.Adam(vae.parameters())
vae.train()
for epoch in range(epoch_num):
for x,_ in dataloader:
x = x.to(device)
# vaeのforward()を使用せずにそのまま誤差の出力
loss = criterion(x)
optimizer.zero_grad()
loss.backward()
optimizer.step()
補足
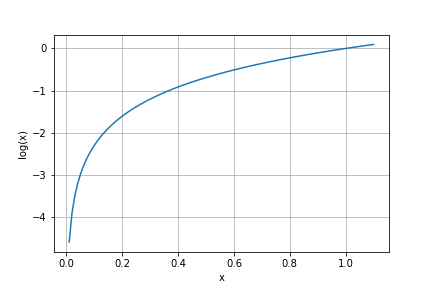
対数グラフ
- xが0近づくほど負の値が大きくなる
- xが1に近づくほど0に近くなる
クロスエントロピー誤差について
-
$ H(p,q) = - \frac{1}{N} \sum^{N}_{i=1}p(x_i)log(q(x_i)) $
- pが真の確率分布、qが推定した確率分布となります
- pとqの確率分布が似ていると誤差は小さくなり、差が大きいほど誤差が大きくなります
-
例
- 真の確率分布[1 0 0] 推定した確率分布[0.5, 0.3, 0.2] = 0.23104906018664842
- 真の確率分布[0 1 0] 推定した確率分布[0.7, 0.1, 0.2] = 0.7675283643313485
- 真の確率分布[1 0 0] 推定した確率分布[0.5, 0.4, 0.1] = 0.23104906018664842
-
問題点として例1と例3は推定した確率分布が同じになってしまいます。
クロスエントロピー誤差では真の分布上の正解値(1)以外の部分は特に重視しないという問題があります。
バイナリークロスエントロピー誤差
$ H(p,q) =- \sum^{N}_{i=1}p_i log q_i = -ylogy'-(1-y)log(1-y') $
- 先ほどのクロスエントロピー誤差は正解値(1)以外の部分を重視しないという問題点が存在しました。
以上のような数式にすることで正解値(1)以外の部分についても考慮した計算ができます - 例
- 真の確率分布[1 0 0] 推定した確率分布[0.5, 0.3, 0.2] = 0.4243218919376292
- 真の確率分布[0 1 0] 推定した確率分布[0.7, 0.1, 0.2] = 0.22839300363692283
- 真の確率分布[1 0 0] 推定した確率分布[0.5, 0.4, 0.1] = 0.43644443999458743