最近ゲーム制作となるとUnityかUE4かみたいなところがあると思うんですけど、なぜかどっちにもパラメトリック曲線を使ってあれこれする機能がないのでちょっと不便だなとか思ってます(もしかしたら知らないだけであるかもしれません)。まぁ最近のゲームとか簡単なのだと使わなくてもなんとかなったりしなくもないですが、知ってるとかっこよかったり(?)「ちょっとだけ敵を凝った動きにしたい」なんてときに役立ったりするかもしれないので、頭の片隅にでも入れておくといいかもしれません。というわけでパラメトリック曲線の中で一番理解しやすい(と思われる)**エルミート曲線(Hermite Curve)**の紹介です。今更感あるとは思いますけど。
免責事項/対象読者
エルミート曲線について、自分なりに適当に噛み砕いて説明するだけなので目新しいようなものとかは特に無いです。あと、私はバリバリの数学屋ではないので計算のところとかはかなり適当にやります。分からない程度にはしないと思いますが分かる程度に端折ります。
読者対象として想定しているのはタイトルの通り「趣味でゲームを作っている人/作り始めた人」になりますが、最近は一般のアプリでもなんかやたらUI要素がかっこいい感じに動いたりしてるので、ゲーム作らない人でも参考になる部分はあるかもしれません。
あ、でも普通は面倒だしビルトインのアニメーション使いますよね......そうですよね......
あと簡単に微分が出てくるので高校3年入門程度の数学力が必要です。
パラメトリック曲線とは
一般的には「パラメータtによって定義される点(f(t), g(t))をプロットしてできる曲線」のことです。3次元に拡張できないこともなくはないですが話が逸れそうなので最後にちょっとだけ出しておきます。
パラメトリック曲線として最もよく知られているものとして「ベジェ曲線」があると思います。正確には(中身の実装方法にもよる気がしますが)「3次ベジェ曲線」といいます。これは先のf, gの中の式が3次式になっているためです。同じ流れで「2次ベジェ曲線」というのもあります。3次ベジェ曲線は制御点が4つあるのに対し2次ベジェ曲線は制御点は3つです。今回紹介するエルミート曲線は制御点が4つのタイプの曲線になります。
実際にどんな感じなの/どんな場面で使えるの?
ゲーム作る人はだいたい完成物を先に見ないとモチベーションが上がらないみたいなところがあると思います。私です。とりあえず適当に描画するソフトを作ったのでそのスクリーンショットをどうぞ。
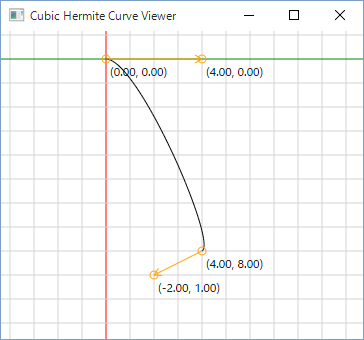
オレンジ色の円が制御点になります。黒の線が実際の曲線になります。あんまり派手ではないですね。
さてこのエルミート曲線、ざっくりと噛み砕いて説明するなら「ここ(始点)からここ(終点)まで、この速度で動いてね」というのを指定してあげるとそんな感じに動いてくれる、というのを式ひとつ(正確にはx,yで2つ)で定義できます。そのため、例えばシューティングの敵の動きをちょっと複雑にしたい場合などに使えると思います。ほぼ直感にしたがって動いてくれるので調整が楽です。
ただ難点があって、上の画像からも分かる通り速度ベクトルの影響度が非常に小さいです。そのため、かなり速度が遅かったりするとほぼ直線移動に見えてしまったりして、特性を知らないと変に悩まされると思います。その場合は速度ベクトルをn倍してあげればだんだんマシになってきます。
式を求める
説明ばかり聞いてても実装できるはずがないので、そろそろ式を求め始めます。
今回はまず上の画像の曲線の式を求めてみましょう(いきなり汎用化してもわからないと思うので......)。
今回の制御点たちをこう定義しておきます。
(x_1, y_1) = (0, 0) \hspace{2em} \vec{v_1} = (v_{x1}, v_{y1}) = (4, 0)\\
(x_2, y_2) = (4, 8) \hspace{2em} \vec{v_2} = (v_{x2}, v_{y2}) = (-2, 1)
$(x_1, y_1), (x_2, y_2)$が始点と終点、$\vec{v_1}, \vec{v_2}$が各速度ベクトルです。
エルミート曲線は制御点が4つありますので、3次の多項式を考えます。(考え方としてもう一個、この曲線はパターンによってはS字の曲線を描くので、3次関数のグラフに似てるな~、ってことは3次の多項式になりそうかな、という感じでも大丈夫だと思います。そうならないパターンももしかしたらあるかもしれないので保証はしません。)
3次の多項式を考えるということで、まずはそれを置いておきます。最終形をしっかり固めてからのほうがいいというのはものづくりでも同じですね。
f_x(t) = at^3 + bt^2 + ct + d\\
f_y(t) = et^3 + ft^2 + gt + h
あ、ここで$0 \leq t \leq 1$としておきます。
a~hを求めていくことになります。まずわかりやすいところで$t=0$と$t=1$のときの式を定義します。これは要するに端っこの座標を定義することになります。
f_x(0) = d = 0 \hspace{2em} f_x(1) = a + b + c + d = 4 \\
f_y(0) = h = 0 \hspace{2em} f_y(1) = e + f + g + h = 8
あとはa, b, c, e, f, gを求めればおしまいです。これは微分を使って求めます。なぜ微分かというと、先の説明を思い出してほしいのですが、エルミート曲線は端っこの速度を指定してあげるとそれを適当に補間しながら曲線を作ります。なので、速度ベクトルがどう変化しているかを知ることができればそれを積分することで曲線の式を得ることができます。今やってるやつと手順が逆ですけど考え方としてはそんな感じです。速度ベクトルの変化を得るために$f_x, f_y$をそれぞれ微分します。
f_x'(t) = 3at^2 + 2bt + c \\
f_y'(t) = 3et^2 + 2ft + g
ここでも先ほどと同じように端っこの式を定義します。今回は微分したので速度ベクトルに関する式となります。
f_x'(0) = c = 4 \hspace{2em} f_x'(1) = 3a + 2b + c = -2 \\
f_y'(0) = g = 0 \hspace{2em} f_y'(1) = 3e + 2f + g = 1
ここで、$t=0$の側の式を使って$t=1$の側の式をまとめます。
a + b + 4 + 0 = 4 \Rightarrow a + b = 0 \\
e + f + 0 + 0 = 8 \Rightarrow e + f = 8 \\
3a + 2b + 4 = -2 \Rightarrow 3a + 2b = -6 \\
3e + 2f + 0 = 1 \Rightarrow 3e + 2f = 1
これは左辺がaとbの式、eとfの式でまとめて連立方程式にできます。
\left\{
\begin{array}{}
a + b &= 0 \\
3a + 2b &= -6
\end{array}
\right. \hspace{2em}
\left\{
\begin{array}{}
e + f &= 8 \\
3e + 2f &= 1
\end{array}
\right.
連立方程式にしてしまえば、あとは解くだけです。ここではbおよびfを代入で消去する方法でやります。
b = -a \\
3a - 2a = -6 \\
\begin{align}
a &= -6 \\
b &= -(-6) \\
&= 6 \\
(a, b) &= (-6, 6)
\end{align}
f = 8 - e \\
3e + 16 - 2e = 1 \\
\begin{align}
e &= -15 \\
f &= 8 + 15 \\
&= 23 \\
(e, f) &= (-15, 23)
\end{align}
これでa~hがすべて求まりました。代入すると、最終的に以下の式を得られます。
f_x(t) = -6t^3 + 6t^2 + 4t \\
f_y(t) = -15t^3 + 23t^2
以上の手順で係数を求めることができます。できますとは言ってもこれを覚えて毎回手作業でやるのはしんどいですし、このままではパラメータ調整しようにもどこをどういじったものか、一箇所だけいじればいいものをかなりの量いじらないといけなくなるのでプログラマ的にも(そうでなくても)心労が溜まるので汎用化します。
汎用化(一般化)
上の式の数値を変数に置き換えただけです。意味は上のものと同じです。
\begin{align}
f_x(t) &= at^3 + bt^2 + ct + d \\
f_y(t) &= et^3 + ft^2 + gt + h \\
f_x'(t) &= 3at^2 + 2bt + c \\
f_y'(t) &= 3et^2 + 2ft + g
\end{align}
\begin{align}
f_x(0) &= d = x_1 &\hspace{1em} f_x(1) &= a + b + c + d = x_2 \\
f_y(0) &= h = y_1 &\hspace{1em} f_y(1) &= e + f + g + h = y_2 \\
f_x'(0) &= c = v_{x1} &\hspace{1em} f_x'(1) &= 3a + 2b + c = v_{x2} \\
f_y(0) &= g = v_{y1} &\hspace{1em} f_y'(1) &= 3e + 2f + g = v_{y2}
\end{align}
\left\{
\begin{array}{}
a + b &= x_2 - x_1 - v_{x1} \\
3a + 2b &= v_{x2} - v_{x1}
\end{array}
\right. \hspace{1em}
\left\{
\begin{array}{}
e + f &= y_2 - y_1 - v_{y1} \\
3e + 2f &= v_{y2} - v_{y1}
\end{array}
\right.
b = x_2 - x_1 - v_{x1} - a \\
3a + 2x_2 - 2x_1 - 2v_{x1} - 2a = v_{x2} - v_{x1} \\
\begin{align}
a &= v_{x2} - v_{x1} - 2x_2 + 2x_1 + 2v_{x1} \\
&= v_{x2} + v_{x1} - 2x_2 + 2x_1 \\
b &= x_2 - x_1 - v_{x1} - v_{x2} - v_{x1} + 2x_2 - 2x_1 \\
&= 3x_2 - 3x_1 - 2v_{x1} - v_{x2}
\end{align}
f = y_2 - y_1 - v_{y1} - e \\
3e + 2y_2 - 2y_1 - 2v_{y1} - 2e = v_{y2} - v_{y1} \\
\begin{align}
e &= v_{y2} - v_{y1} - 2y_2 + 2y_1 + 2v_{y1} \\
&= v_{y2} + v_{y1} - 2y_2 + 2y_1 \\
f &= y_2 - y_1 - v_{y1} - v_{y2} - v_{y1} + 2y_2 - 2y_1 \\
&= 3y_2 - 3y_1 -2v_{y1} - v_{y2}
\end{align}
\left\{ \begin{array}{}
\begin{align}
f_x(t) &= (2x_1 - 2x_2 + v_{x1} + v_{x2})t^3 + (-3x_1 + 3x_2 - 2v_{x1} - v_{x2})t^2 + v_{x1}t + x_1 \\
f_y(t) &= (2y_1 - 2y_2 + v_{y1} + v_{y2})t^3 + (-3y_1 + 3y_2 - 2v_{y1} - v_{y2})t^2 + v_{y1}t + y_1
\end{align}
\end{array} \right.
終わりに
ここまで長々と係数を求めてきたわけですが、正直のところこんなことはしなくてもよかったりします。というのは、エルミート曲線というのはエルミート多項式にしたがっているためです。これはいわゆる補間の手法の一つで用いられるものです。エルミート多項式を使った曲線式はもうちょっと簡素になるのですが、多分理解するのが難しい気がするので紹介しません(気になる人は自分で調べてください)(というか私も理解できてません)。理解する必要がないという人もいたりしますが、まぁ巷のゲームライブラリならだいたい曲線もカバーしててクラス一個で描画からアニメーションまでなんでもやってしまうので確かに無理に理解する必要ないかもな~、みたいなところはあります。
あと先頭のあたりで言ってた多次元化ですが、たぶん勘のいい方なら気づくと思いますが式中のx, yの文字を変えれば簡単にできます。逆に次元を減らすことも可能です。
参考文献
http://1st.geocities.jp/shift486909/program/hermite.html
http://ksgeo.kj.yamagata-u.ac.jp/~kazsan/class/geomath/bibun-kiso.html
微積分すっかり忘れてしまってて非常によろしくないですね......