【量子シミュレータ】DB検索などの応用が期待されるGroverアルゴリズムの実装

はじめに

量子コンピュータはまだまだ一般に普及しているとは言えないため、量子アルゴリズムの動作確認を実施する際には、古典コンピュータ（i.e. 古典ビット{0,1}を扱うコンピュータ）上で動作する量子シミュレータが利用されます。量子シミュレータは、Qiskitなど様々なものが公開されていますが、特定のアルゴリズムの実装に重きをおけば、量子シミュレータの自作も比較的容易にできます。
本記事では、Groverアルゴリズムを対象に自作した量子シミュレータを紹介します。Groverアルゴリズムとは、ゲート型量子コンピュータの利用を前提とした量子アルゴリズムの一種で、データベース（以降は、DB）の検索などへの応用が期待されているものです。
自作した量子シミュレータの特徴は、GroverアルゴリズムにおけるOracle回路（検索したいインデックスに応じて変更が必要な量子回路）を自動生成してくれる点にあります。参考文献のように、検索したいインデックスがある特定の値である場合から一歩進み、検索したいインデックスがどのような値でも対応できるようにするために、量子シミュレータをどう実装すればいいかを理解する助けになればと思っています。

参考文献

Groverアルゴリズムの理解や量子シミュレータの作成の際に、参考にした文献を示します。本記事を読み進める前提となっていますので、一読していただくことをお勧めします。

注意事項

Groverアルゴリズムは、上記参考文献[1,2]を含め、様々な文献で説明されています。本記事では、Groverアルゴリズム自体の説明は割愛し、Groverアルゴリズムを量子シミュレータとして実装する際のポイントのみを説明します。

対象読者

・量子アルゴリズムに関心がある人
・量子シミュレータの実装に関心がある人
・データベースの検索アルゴリズムに関心がある人

本記事の目的

・自作量子シミュレータの概要と実行手順の説明
・Groverアルゴリズムを実装する際のポイントの説明（注：2.2節が重要です。）

目次

1. 自作した量子シミュレータの概要と実行手順
2. Groverアルゴリズムの実装上のポイント
3. まとめ

本文

1. 自作した量子シミュレータの概要と実行手順

自作した量子シミュレータの概要や、実行手順に関する説明をします。
自作した量子シミュレータは下記リンクのGithubにて公開しています。

本記事では、tag v1.0のものを利用しています。
git cloneして頂ける場合は、以下のコマンドを参考にして下さい。

git clone https://github.com/Alaska-Panda/QuaPan.git - b v1.0 --depth 1

1.1 量子シミュレータの概要

自作した量子シミュレータはGroverアルゴリズムの実行に特化しています。
Groverアルゴリズムとは、例えば、N個の量子ビットで表現される$2^N$個のデータを含むDBの中からインデックスがKのものを検索したい場合に、量子ビットの重ね合わせ状態を利用した計算を行うことで高速な検索を可能にするアルゴリズムです。
自作した量子シミュレータの特徴は、検索に用いるインデックスに応じて修正が必要なOracle回路を自動で生成できることです。
Oracle回路については後述しますので、検索したいインデックスが変わる度に、回路を用意しなければならない点だけを覚えておいて下さい。

1.2 Groverアルゴリズムの実行

Githubから入手した量子シミュレータのalgorithmsのフォルダに移動し、格納されているauto_grover.pyを実行します。

cd QuaPan/algorithms/
python3 auto_grover.py 4 7 1

実行時の引数

第一引数は量子ビット数（1.1節の説明におけるNに対応するもの）です。
例えば、量子ビット数を3とした場合は、シミュレータ内に0番から7番のインデックスに紐付いた8つのデータが生成されます。
第二引数は検索するインデックスの番号（1.1節の説明におけるKに対応するもの）です。
第三引数はシミュレータ上での検索を実施するかを表すフラグです。1の場合は実施する、0の場合は実施しないに対応します。
基本的に1を指定すれば良いですが、Nを大きくした場合はシミュレーションに時間がかかるため、0にして様子を伺うこともできます。

シミュレータの実行結果

先に示したコマンドは、4量子ビット数で表現されるDBから、インデックス7のデータを検索する場合のコマンドとなります。
コマンドの実行後、下図のように各データが正解である確率がグラフで表示され、インデックス7に対応するデータが正解である確率が最も高いことが分かります。

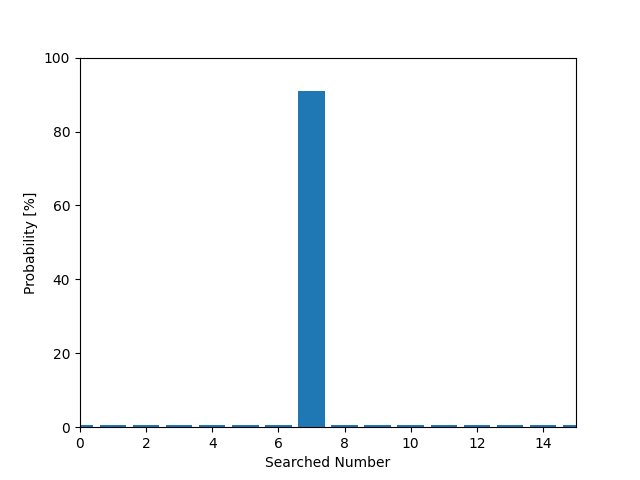
実行後のコマンドライン上には、以下のように生成された量子回路やシミュレーションの実行結果の数値データが表示されます。
量子回路は、複数個（シミュレーション上の繰り返し回数分）のOracle回路とDiffuser回路が直列で繋がった回路です。
今回の表示では、量子回路が食い上がっていく仮定を表示しています。従って、量子回路として最終的に利用するのは最終段のものになります。

# python3 auto_grover.py 4 7 1
NUMBER OF ITERATIONS : 3
Oracle x 1 :Diffuser x 0
matrix size :  4 x 3
['X', '*', 'X']
['-', '*', '-']
['-', '*', '-']
['-', 'Z', '-']
Oracle x 1 :Diffuser x 1
matrix size :  4 x 8
['X', '*', 'X', 'H', 'X', '*', 'X', 'H']
['-', '*', '-', 'H', 'X', '*', 'X', 'H']
['-', '*', '-', 'H', 'X', '*', 'X', 'H']
['-', 'Z', '-', 'H', 'X', 'Z', 'X', 'H']
Oracle x 2 :Diffuser x 1
matrix size :  4 x 11
['X', '*', 'X', 'H', 'X', '*', 'X', 'H', 'X', '*', 'X']
['-', '*', '-', 'H', 'X', '*', 'X', 'H', '-', '*', '-']
['-', '*', '-', 'H', 'X', '*', 'X', 'H', '-', '*', '-']
['-', 'Z', '-', 'H', 'X', 'Z', 'X', 'H', '-', 'Z', '-']
Oracle x 2 :Diffuser x 2
matrix size :  4 x 16
['X', '*', 'X', 'H', 'X', '*', 'X', 'H', 'X', '*', 'X', 'H', 'X', '*', 'X', 'H']
['-', '*', '-', 'H', 'X', '*', 'X', 'H', '-', '*', '-', 'H', 'X', '*', 'X', 'H']
['-', '*', '-', 'H', 'X', '*', 'X', 'H', '-', '*', '-', 'H', 'X', '*', 'X', 'H']
['-', 'Z', '-', 'H', 'X', 'Z', 'X', 'H', '-', 'Z', '-', 'H', 'X', 'Z', 'X', 'H']
Oracle x 3 :Diffuser x 2
matrix size :  4 x 19
['X', '*', 'X', 'H', 'X', '*', 'X', 'H', 'X', '*', 'X', 'H', 'X', '*', 'X', 'H', 'X', '*', 'X']
['-', '*', '-', 'H', 'X', '*', 'X', 'H', '-', '*', '-', 'H', 'X', '*', 'X', 'H', '-', '*', '-']
['-', '*', '-', 'H', 'X', '*', 'X', 'H', '-', '*', '-', 'H', 'X', '*', 'X', 'H', '-', '*', '-']
['-', 'Z', '-', 'H', 'X', 'Z', 'X', 'H', '-', 'Z', '-', 'H', 'X', 'Z', 'X', 'H', '-', 'Z', '-']
Oracle x 3 :Diffuser x 3
matrix size :  4 x 24
['X', '*', 'X', 'H', 'X', '*', 'X', 'H', 'X', '*', 'X', 'H', 'X', '*', 'X', 'H', 'X', '*', 'X', 'H', 'X', '*', 'X', 'H']
['-', '*', '-', 'H', 'X', '*', 'X', 'H', '-', '*', '-', 'H', 'X', '*', 'X', 'H', '-', '*', '-', 'H', 'X', '*', 'X', 'H']
['-', '*', '-', 'H', 'X', '*', 'X', 'H', '-', '*', '-', 'H', 'X', '*', 'X', 'H', '-', '*', '-', 'H', 'X', '*', 'X', 'H']
['-', 'Z', '-', 'H', 'X', 'Z', 'X', 'H', '-', 'Z', '-', 'H', 'X', 'Z', 'X', 'H', '-', 'Z', '-', 'H', 'X', 'Z', 'X', 'H']
--Simulation--
--Probabilities in Simulation--
# 0 : 0.6 [%]
# 1 : 0.6 [%]
# 2 : 0.6 [%]
# 3 : 0.6 [%]
# 4 : 0.6 [%]
# 5 : 0.6 [%]
# 6 : 0.6 [%]
# 7 : 90.8 [%]
# 8 : 0.6 [%]
# 9 : 0.6 [%]
# 10 : 0.6 [%]
# 11 : 0.6 [%]
# 12 : 0.6 [%]
# 13 : 0.6 [%]
# 14 : 0.6 [%]
# 15 : 0.6 [%]
Estimated Answer : 7
Probability of Answer [%] : 90.8

2. Groverアルゴリズムの実装上のポイント

Groverアルゴリズムは以下のフローとなります。
各ステップの説明を自作量子シミュレータのコードを引用しながら説明します。

Groverアルゴリズムのフロー

1. 検索対象のデータセットを量子ビットで表す。
2. Oracle回路にステップ1 or 2の量子状態を入力する。
3. Diffuser回路にステップ2の量子状態を入力する。
4. 繰り返し回数が規定回数を超えるまで2に戻る。
5. 最も確率が高い量子状態を解とする。

2.1 検索対象のデータセットを量子ビットで表す。

先ずは各データのインデックスを古典ビットで表します。古典ビットで表した情報は、重ね合わせのない量子状態と考えることもできます。量子アルゴリズムでは、量子ビットが重ね合わさった状態を利用した計算を実施することで、計算の高速化などを達成します。量子ビットの重ね合わせ状態を作るために、古典ビットを複素ベクトルである量子ビットで表し、アダマールゲートを通過させます。これにより、量子ビットの重ね合わせ状態を作り出すことができます。

自作量子シミュレータのプログラムとしては以下の部分が対応しています。

QuaPan/algorithms/auto_grover.py

	QC_INPUT  = input_h(NQ_Data,NQ_Index)

QuaPan/core/input.py

def input_h(K,M=0):
	QC = QuCircuit(K,M)
	QC.h(range(0,K+M))
	QC.add()
	QC.tdot()
	A = QC.rt_QMatrix()
	return A[0]

2.2 Oracle回路に量子状態を入力する。

DBの検索は、簡単に言えばパターンマッチです。このパターンマッチに相当するものが、Oracle回路です。
Orale回路がパターンマッチの役割であることから分かるように、検索したいデータに応じて、回路を変える必要があります。
今回の量子シミュレータでは、自動でOracle回路を生成するoracle関数を用意しました。
Oracle回路は、CZゲートをXゲート（量子ビットのフリップに相当する）で挟み込む構造となっています。仮にOracle回路がCZゲートのみの構造となっていた場合、ビット表記でオール1に相当するインデックスが最終的に正解として得られます。従って、oracle関数の仕組みは、検索したいインデックスとオール1のXORを取り、1が残った箇所にある量子ビットに対して、量子ビットのフリップに相当するXゲートを適用するというものとしました。
Oracle回路の具体例をいくつか示します。例えば、4量子ビットでインデックス0のデータを検索したい場合のOracle回路は以下となります。全ての量子ビットに対して、Xゲートが作用していることが分かります。

['X', '*', 'X']
['X', '*', 'X']
['X', '*', 'X']
['X', 'Z', 'X']

次は、4量子ビットでインデックス1のデータを検索したい場合のOracle回路です。最下位の量子ビットのみ、Xゲートが作用しないものとなっていることが分かります。古典ビットのXOR演算からOracle回路の構成を決められることが読み取れると思います。

['X', '*', 'X']
['X', '*', 'X']
['X', '*', 'X']
['-', 'Z', '-']

参考として、上記に対応する量子シミュレータのコードを示します。

QuaPan/algorithms/auto_grover.py

		# Oracle
		print("Oracle x",i+1,":Diffuser x",i)
		oracle(QC,NQ_ALL,SEARCH_PATTERN)
		QC.add()
		QC.cz(range(0,NQ_ALL-1),NQ_ALL-1)
		QC.add()
		oracle(QC,NQ_ALL,SEARCH_PATTERN)
		QC.add()
		QC.show_ALL()

QuaPan/algorithms/auto_grover.py

def oracle(QC,NQubits,PATTERN):
	mask = (1<<NQubits) - 1
	A = PATTERN ^ mask
	for i in range(NQubits):
		if ((A >> (NQubits - i -1))  & 1):
			QC.x(i)

2.3 Diffuser回路に量子状態を入力する。

Diffuser回路は、検索対象のインデックスを持つデータが正解である確率を増幅させる効果があります。検索対象のインデックスに依存しないため、インデックスが変わる度に回路を修正する必要はありません。

2.4 繰り返し回数が規定回数を超えるまで2に戻る。

Groverアルゴリズムによって正解データが見つかる確率を高くするためには、Oracle回路とDiffuser回路を用いた繰り返し計算が必要です。
繰り返し規定回数は、量子ビット数をNとした場合に、以下の数式から求めることができます。

\frac{\pi}{4}\sqrt{2^N}

2.5 最も確率が高い量子状態を解とする。

最終的な量子状態を観測します。各量子状態（e.g. |011>）の係数は、データが正解である確率を示しています。
最も高い確率のデータを正解として判定します。

3. まとめ

本記事では、Groverアルゴリズムを対象に自作した量子シミュレータの紹介として、上記シミュレータを用いたGroverアルゴリズムの実行方法や、Groverアルゴリズムを実装する際のポイントを説明しました。