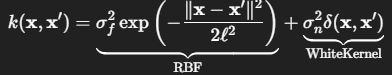目的
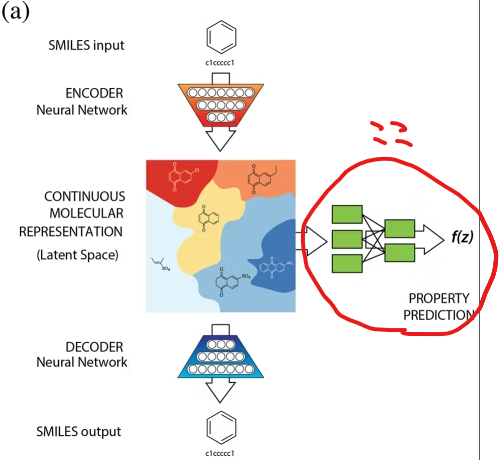
この論文↓の追試がそもそものきっかけです。
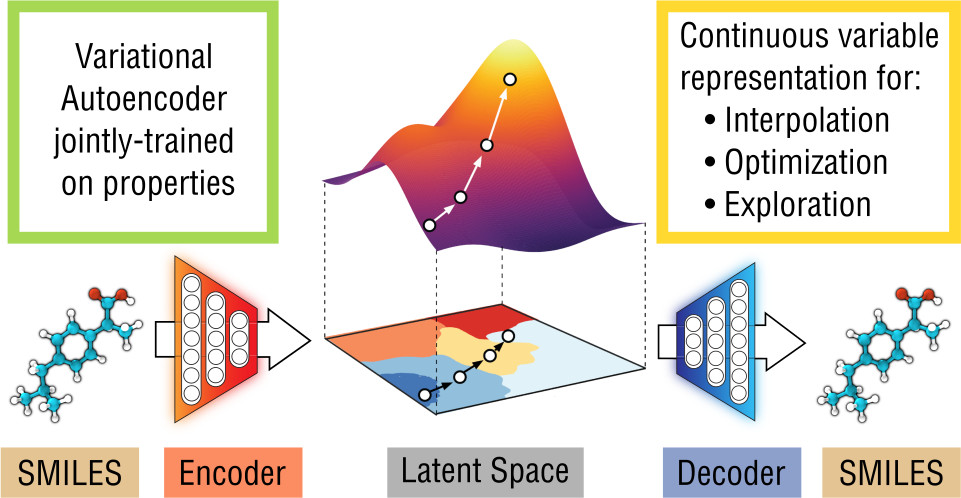
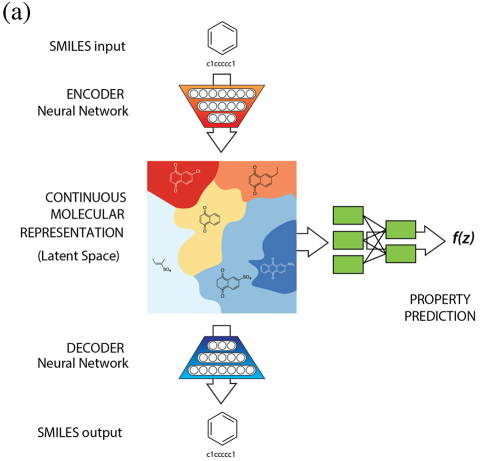
「Automatic Chemical Design Using a Data-Driven Continuous Representation of Molecules」, ACS Cent. Sci. 2018, 4, 2, 268–276, , https://doi.org/10.1021/acscentsci.7b00572
いわゆるChemical VAEというやつで、既存分子を入力すると、似ているが違う分子を生成してくれます。Githubにサンプルコードがあったり、すでに別の方がブログでとりあげて使っています。
ただ、コードはTensorflowで書かれており、PyTorchユーザーである私にはアレンジ不可能で、うまく使いこなすことができませんでした。また生成される有効な分子の数も少ないらしい。Chemical VAEというものを初めて作った業績はすばらしいですが、もう少し使いやすくしたいというのが本音です![]()
以前、Chemical VAEらしきものは実装できたのですが、物性を予測する予測ヘッドは実装しておらずVAEのみでした。論文では、新しい分子を生成するだけでなく、その分子の物性の予測も行っていたのです。
そこで今回は、論文の流れをある程度汲み取り、修正できる部分を修正して使いやすいようにアレンジしてみました。
大きく修正した部分は以下の通りです。
- tensorflowではなくPyTorchを使用
- SMILESではなくSELFIESを使用することで有効な分子を増やす
- ConvエンコーダをGRUエンコーダに変更
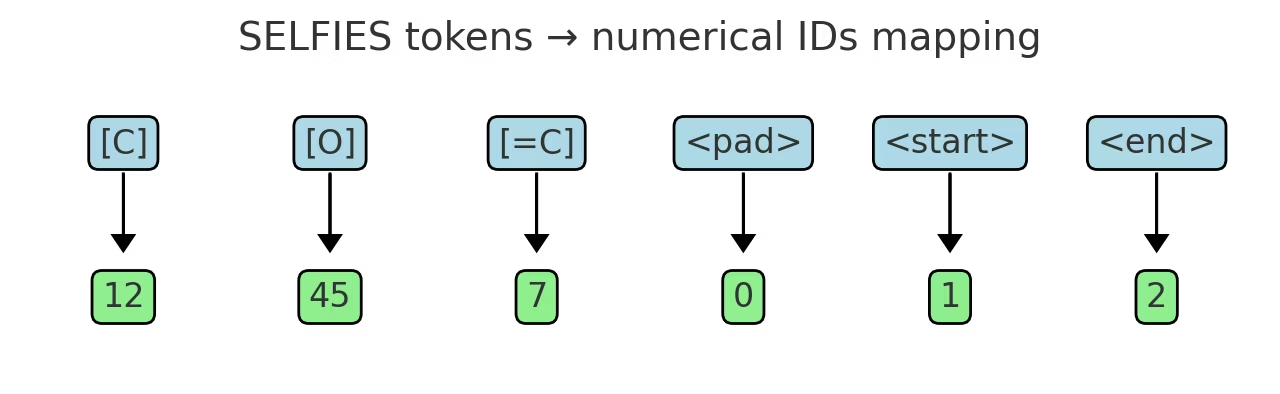
おそらく論文では、SMILESをOne-HotベクトルにしてConvに入力しています。今回の場合、SELFIESをtoken、整数IDに変換してEmbedding層でベクトルに変換します。
ちなみにSELFIESという分子表記法を作った人もChemical VAEを作った人と同じで、Alán Aspuru-Guzik教授とのこと!!
SELFIES は「どんな文字列でも必ず有効な分子になる」100%ロバストな分子表現で、SMILES のように壊れた分子が生成される問題を根本的に解決し、深層学習・進化計算などの生成モデルでそのまま使えるため、分子設計の探索効率と多様性が大きく向上します(チャッピーより)。要は、SMILESだと有効な分子を作りだすのが難しい場合でも、SELFIESだとその障壁が低くなると解釈しています。
結果として、SMILESでは有効な分子の数が少なかったのに対して、SELFIESだと有効な分子の割合が増えました![]()
実装
データセットの読み込み・前処理
今回使ったライブラリのversionは以下の通りです。
=== Environment ===
Python : 3.9.23
=== Library versions ===
numpy : 1.26.4
pandas : 2.3.3
matplotlib : 3.9.4
torch : 2.8.0+cu128
tqdm : 4.67.1
selfies : 2.1.1
kagglehub : 0.3.13
rdkit : 2025.03.5
scikit-learn: 1.6.1
scipy : 1.13.1
Pillow : 11.3.0
まずは論文で使用されているデータセットであるZINCをダウンロードします。ZINC は創薬研究の初期段階で使用される「薬らしい」低分子化合物データベース です(私自身薬専門ではないですが、結構有名なデータセットらしい)。
QED、logPなど 創薬で重要な分子特性 を満たすよう設計されています。今回は、kagglehubというライブラリを使ってインストールしました。以下のコードで使えるようになります。
import kagglehub
# Download latest version
path = kagglehub.dataset_download("basu369victor/zinc250k")
print("Path to dataset files:", path)
Path to dataset files: /root/.cache/kagglehub/datasets/basu369victor/zinc250k/versions/1
そしてこのパスを使用してcsvを読み込み、中身を見てみます。
# 読み込み
csv_path = os.path.join(path, "250k_rndm_zinc_drugs_clean_3.csv")
df_zinc = pd.read_csv(csv_path)
print("Shape:", df_zinc.shape)
print(df_zinc.head())
Shape: (249455, 4)
smiles logP qed \
0 CC(C)(C)c1ccc2occ(CC(=O)Nc3ccccc3F)c2c1\n 5.05060 0.702012
1 C[C@@H]1CC(Nc2cncc(-c3nncn3C)c2)C[C@@H](C)C1\n 3.11370 0.928975
2 N#Cc1ccc(-c2ccc(O[C@@H](C(=O)N3CCCC3)c3ccccc3)... 4.96778 0.599682
3 CCOC(=O)[C@@H]1CCCN(C(=O)c2nc(-c3ccc(C)cc3)n3c... 4.00022 0.690944
4 N#CC1=C(SCC(=O)Nc2cccc(Cl)c2)N=C([O-])[C@H](C#... 3.60956 0.789027
SAS
0 2.084095
1 3.432004
2 2.470633
3 2.822753
4 4.035182
25万ほどのデータが入っていることが分かりました。もともとはさらに大きなデータセットらしいですが、それを一部抜粋したものらしい。それでもかなり大きなデータセットです。目的変数にできる変数は三つあり、それぞれ、
-
logP : 分子が水と油のどちらに溶けやすいかを示す値。値が大きいほど油に溶けやすく、小さいほど水に溶けやすい。薬の体内移動性を判断する指標
-
qed : 分子が“薬としてふさわしい性質”をどれだけ満たしているかを0〜1で表す指標。1に近いほど薬として理想的な分子
-
SAS : 分子がどれくらい“合成しやすいか”を1〜10で評価する指標。小さいほど作りやすく、大きいほど合成が難しい分子
とのこと。いかにも創薬の指標って感じ。
データセットの読み込みが完了したので、次は前処理を行います。
# SMILESをSELFIESに変換
dataset = df_zinc.copy()
dataset["mol"] = dataset["smiles"].apply(lambda s: Chem.MolFromSmiles(s) if pd.notna(s) else None)
dataset = dataset.dropna(subset=["mol"]) # ここで目的変数とmolの行が揃う
dataset["can_smiles"] = dataset["mol"].apply(lambda m: Chem.MolToSmiles(m, canonical=True, isomericSmiles=True)) # isomericSmiles=True は、立体化学を含めたSMILESを生成
dataset["SELFIES"] = dataset["can_smiles"].apply(sf.encoder)
print("Unique canonical SMILES:", dataset["can_smiles"].nunique())
print("Unique SELFIES:", dataset["SELFIES"].nunique())
Unique canonical SMILES: 249455
Unique SELFIES: 249455
何をやっているかというと、
smilesからmolの作成→
molから正規化smilesの作成→
正規化smilesからSELFIESの作成
を行っています。同じ分子でもSMILESだと複数の表現があるため(エタノールの例だと、"CCO", "OCC")、このままだと重複扱いされず、モデルが別の分子として学習してしまう可能性があります。そこで、canonical SMILESにすると、同一構造なら同じ表記になり、「分子構造の正しいユニーク数」となります。SELFIESはSMILESに影響を受けるため、いきなりSMILESからSELFIESを作るのではなく、このような処理を行っています。
SELFIESが用意できたので、一度保存しておきましょう。んで、再度読み込みます。
# 保存しておく
dataset.to_csv("data/zinc250k.csv", index=False)
# 再度呼び出し
dataset = pd.read_csv("data/zinc250k.csv", index_col=None)
dataset.head()
いい感じです。それでは、VAEの構築・学習に進みます。
文字列の変換
今回はVAE単体だけではなく、目的関数の予測を行うNNも構築します。マルチタスク学習というやつです。
Encoder → z(mu, logvar) →
├─ Decoder(SELFIES再構成タスク / sequence task)
└─ MLP(物性予測タスク / regression task)
エンコーダから出力される潜在変数を使って、再構築を行うタスクと物性予測を行うタスクを実施します。よって、物性予測を行うためには汎化性能を評価する必要があるため、まず、データセットを学習と検証に分けます。
そして、学習データから、SELFIESの文字(トークン)のアルファベット表を作ります。最終的にSELFIESが使うトークンの辞書を構築するためです。要は、VAEのEmbedding層で使うID辞書を作っています。
# Hold-out
train_df, val_df = train_test_split(dataset, test_size=0.2, random_state=1234, shuffle=True)
# アルファベットは train の SELFIES から作る→リーク防止
train_selfies_list = train_df["SELFIES"].tolist()
alphabet = sf.get_alphabet_from_selfies(train_selfies_list) # 出現トークン集合
alphabet = sorted(list(alphabet)) # 再現性のためにソート
special = ["<pad>", "<start>", "<end>", "<unk>"]
tokens = alphabet + special
# stoi/itos と特殊トークンID
stoi = {t: i for i, t in enumerate(tokens)}
itos = {i: t for t, i in stoi.items()}
pad_idx = stoi["<pad>"]
start_idx = stoi["<start>"]
end_idx = stoi["<end>"]
unk_idx = stoi["<unk>"]
print("vocab size:", len(tokens))
vocab size: 107
コードの説明としては、
① 訓練データのSELFIESを収集
② SELFIESに出てきた全トークンを集める、ソートして決定的な順序にする
③ 特殊トークンを追加する、これがないとデコーダが分子を再構築できない
④ 「文字→ID」と「ID→文字」の辞書を作る
を行っています。全部の分子が同じ長さではないので、padを使って長さを揃えます。また、startとendを用意することで、分子生成の開始と終わりの場所を指定します。
出現したトークンの数は107とのことです。
次に色々関数を定義していきます。
# SELFIESを分割する関数
def selfies_tokens(x): # SELFIESをトークンのリストに分割、=> ["[C]", "[C]", "[O]"]
return list(sf.split_selfies(x))
# 長さの統計を見て上限決め(例:P95)
# 学習用SELFIES長さの95パーセンタイルを上限に採用し、<start>/<end>分を+2
lengths = [len(selfies_tokens(s)) for s in train_selfies_list]
max_len = int(np.percentile(lengths, 95)) + 2 # +2 は <start>/<end> 用
print("max_len:", max_len)
max_len: 54
この処理により、文字列をトークンのリストに変換しています。
例えば、
"[C][C][O][Ring1][Branch1_1]" を
["[C]", "[C]", "[O]", "[Ring1]", "[Branch1_1]"]
のように変換しています。
そして、分子の長さ(大きさ)の統計を取り、その95%を包括するような上限を最大長に設定しておきます。
次はモデルに入力するための変換用関数を定義します。
# エンコード関数(数値化+長さ揃え)、モデルに入れるために数値化+パディング
def encode_selfies(x, max_len=max_len):
# トークン列を作る、例: "[C][O]" → ["[C]","[O]"]、先頭に開始トークン<start>、末尾に終了トークン<end>をつけて、系列の境界を明示
toks = ["<start>"] + selfies_tokens(x) + ["<end>"]
# 語彙辞書でトークンをIDに写像、語彙にないトークンは unk_idx でフォールバックして長さを保つ
ids = [stoi.get(t, unk_idx) for t in toks]
# ちょうど max_len に調整しつつ、切り詰め時は末尾を <end> に保証
if len(ids) >= max_len: # 長すぎる場合、先頭からmax_lenに切り詰め、最後の要素を必ず<end>で上書き
ids = ids[:max_len]
ids[-1] = end_idx
else: # 短い場合、pad_idxで右側を埋めてちょうどmax_lenにする
ids += [pad_idx] * (max_len - len(ids))
return ids # 返り値は長さmax_lenのIDリスト
この関数は、SELFIES文字列をトークン化し、開始・終了記号を付けてID列へ変換し、最大長に合わせてパディングする処理です。分子によっては大きさが異なるので、paddingし、固定長にして長さを揃えます。これにより、VAEに入力することができます。
次に定義する関数は今すぐは使わないですが、VAE学習後に使います。
# ID列→SELFIES文字列に戻す、デコードや可視化で使う
def ids_to_selfies(ids, stop_at_eos=True):
out = []
for i in ids: # end_idx(EOS)に到達したら、stop_at_eos=Trueのとき即終了、生成結果をEOSで綺麗に切り上げるため
if i == end_idx and stop_at_eos:
break
if i in (pad_idx, start_idx, end_idx): # start, end, padは出力に含めない
continue
out.append(itos[i]) # それ以外はitosでトークンに戻してoutに積む
return "".join(out) # SELFIESは "[C][O][N]" のように“トークンがそのまま連結された文字列”なので、単純に join でOK。
これは、モデルの出力ID列を SELFIES トークンへ復元する関数です。pad/start/end を除外し、トークンを結合して SELFIES 文字列へ戻します。分子生成の時に使います。
最後にサンプリング法に関する関数を定義します。
def sample_top_p(logits, p=0.9, temperature=1.05):
"""
これは 「潜在ベクトルから分子を作るときのデコーダ側で、次の文字(トークン)をどう選ぶか」 を制御する関数です。
デコーダが吐いた次のトークンの確率分布(logits)から、どのトークンを選ぶか決める部分
Greedy(確率最大のトークンを選ぶ, argmax)なら毎回一番確率が高いトークンをとる→単調になりがち
Top-p(nucleus)サンプリングは、「累積確率がpを超えるまでの上位候補だけを残し、その中から確率的に選ぶ」という方法
"""
# 温度スケーリング、temp > 1で分布が平ら→多様性増える、temp < 1で分布が尖る→多様性減る
if temperature != 1.0:
logits = logits / temperature
# 確率化&ソート
probs = F.softmax(logits, dim=-1) # [B, V]、確率に変換、logtisはNNの出力層から出てくる確率に変換する前の生のスコア
sorted_probs, sorted_idx = torch.sort(probs, dim=-1, descending=True) # [B, V]、確率の大きい順にソート
cumsum = torch.cumsum(sorted_probs, dim=-1) # [B, V], 確率の大きい順に並べて、累積和をとる
# Top-pフィルタリング、上位から累積確率がp(例:0.9)に達するまで残す、それ以外は確率0にして正規化
mask = cumsum <= p
mask[:, 0] = True # 少なくとも最大確率トークンは残す
filtered = torch.where(mask, sorted_probs, torch.zeros_like(sorted_probs))
filtered = filtered / filtered.sum(dim=-1, keepdim=True)
# サンプリング、残した候補の中から確率に従ってランダムに選ぶ、next_id が次のトークンID
next_rel = torch.multinomial(filtered, 1) # [B,1]
next_id = sorted_idx.gather(-1, next_rel).squeeze(-1) # [B]
return next_id
こちらは、生成時に用いる top-p(nucleus)サンプリングです。確率が累積pを超えるまでの候補だけ残し、その中から確率的に次トークンを選び、多様性と品質を両立させます。
Dataset, DataLoaderの定義
次に用意したデータをPyTorchで扱えるようにDatasetにします。
# Dataset with generic target (logP / qed / SAS / ...)
class SelfiesDataset(Dataset):
def __init__(self, selfies_list, target_values, max_len=120):
self.data = [encode_selfies(s, max_len) for s in selfies_list]
self.target_values = [float(v) for v in target_values] # 明示的に float へ
def __len__(self):
return len(self.data)
def __getitem__(self, i):
x = torch.tensor(self.data[i], dtype=torch.long)
y = torch.tensor(self.target_values[i], dtype=torch.float32) # ← 修正ポイント
return x, y
def collate_xy(batch):
xs, ys = zip(*batch) # ys はすでに tensor(float32)
return torch.stack(xs, 0), torch.stack(ys, 0)
データセットクラスにより、「SELFIES文字列→固定長テンソル」の変換を行います。先ほど定義したencode_selfies関数を使っていますね。コレート関数は1バッチ分のサンプルをまとめてテンソルにする関数です。(X, y)のリストをbatched tensorへ束ねる役割を担います。
それでは、先のデータセットクラスを使って、データローダーを定義していきましょう。
# 使いたいターゲットを指定(例: 'logP', 'qed', 'SAS')
target = 'logP' # ←ここだけ変えればOK
# SELFIES列とターゲット列をリスト化
train_selfies = train_df["SELFIES"].tolist()
train_y = train_df[target].astype(float).tolist()
val_selfies = val_df["SELFIES"].tolist()
val_y = val_df[target].astype(float).tolist()
print(f"Target: {target} | Train: {len(train_selfies)} molecules | Val: {len(val_selfies)} molecules")
# 既に算出済みの max_len(trainのP95+2)をそのまま使用
train_dataset = SelfiesDataset(train_selfies, train_y, max_len=max_len)
val_dataset = SelfiesDataset(val_selfies, val_y, max_len=max_len)
# DataLoaderを準備
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
train_loader = DataLoader(
train_dataset, batch_size=64, shuffle=True,
pin_memory=(device.type == "cuda"), num_workers=2,
collate_fn=collate_xy
)
val_loader = DataLoader(
val_dataset, batch_size=64, shuffle=False,
pin_memory=(device.type == "cuda"), num_workers=2,
collate_fn=collate_xy
)
# 正規化パラメータ(回帰モデル用:trainだけから計算)
y_mean = float(np.mean(train_df[target].astype(float)))
y_std = float(np.std(train_df[target].astype(float)) + 1e-8)
print(f"{target} mean/std (train): {y_mean:.5f} / {y_std:.5f}")
# もし学習ループ側で標準化して使うなら、次のようにdictで保持しておくと便利
norm_stats = {"target": target, "mean": y_mean, "std": y_std}
Target: logP | Train: 199564 molecules | Val: 49891 molecules
logP mean/std (train): 2.45608 / 1.43540
target変数の部分を変更すれば、目的関数を切り替えることができます。今回はlogPを目的変数にしました。先のSelfiesDatasetWithPLを使って、Datasetを用意し、DataLoaderでミニバッチを組みます。この時、先のコレート関数を使います。shuffle=Trueは訓練用のみ設定します。
VAE・損失関数の定義
次はVAEモデルの定義です。このVAEは分子の生成と物性予測を同時に行うマルチタスクVAEとなります。
# VAE with single-target regression (e.g., logP / qed / SAS)
class SelfiesVAEWithRegressor(nn.Module):
"""
SELFIES VAE with single-target regression (logP / qed / SAS など)
target_mean, target_std:
- データの平均/標準偏差で標準化するなら、それらを渡す
- None の場合は (0.0, 1.0) を内部既定として使用
"""
def __init__(self, vocab_size, hidden=256, latent=64, max_len=120,
target_mean=None, target_std=None):
super().__init__()
self.max_len = max_len
# register_buffer: .to(device) に追随し、Optimizer対象外
tm = 0.0 if target_mean is None else float(target_mean)
ts = 1.0 if target_std is None else float(target_std)
self.register_buffer("target_mean", torch.tensor(tm, dtype=torch.float32))
self.register_buffer("target_std", torch.tensor(ts, dtype=torch.float32))
# Embedding
self.embed = nn.Embedding(vocab_size, hidden, padding_idx=pad_idx)
# Encoder
self.encoder_rnn = nn.GRU(hidden, hidden, batch_first=True)
self.mu = nn.Linear(hidden, latent)
self.logvar = nn.Linear(hidden, latent)
# Decoder
self.decoder_rnn = nn.GRU(hidden, hidden, batch_first=True)
self.fc_out = nn.Linear(hidden, vocab_size)
self.latent_to_hidden = nn.Linear(latent, hidden)
# Target regressor (latent -> scalar)
self.target_regressor = nn.Sequential(
nn.Linear(latent, hidden),
nn.ReLU(),
nn.Dropout(0.3),
nn.Linear(hidden, hidden // 2),
nn.ReLU(),
nn.Dropout(0.3),
nn.Linear(hidden // 2, hidden // 4),
nn.ReLU(),
nn.Dropout(0.2),
nn.Linear(hidden // 4, 1)
)
def encode(self, x):
x_emb = self.embed(x) # [B,T,H]
_, h = self.encoder_rnn(x_emb) # h: [1,B,H]
h = h[-1] # [B,H]
return self.mu(h), self.logvar(h)
def reparam(self, mu, logvar):
eps = torch.randn_like(mu)
return mu + eps * (0.5 * logvar).exp()
def predict_target(self, z):
"""Predict selected target (logP/qed/SAS...) from latent z"""
out = self.target_regressor(z)
return out.squeeze(-1) # [B]
def forward(self, x, word_dropout_p=0.15, y_targets=None, deterministic_pred=True):
"""
deterministic_pred=True: 回帰は z_pred=mu(決定論)
戻り値: logits, dec_tgt_ids, mu, logvar, y_pred
"""
mu, logvar = self.encode(x)
# 再構成用 z(train: サンプル, eval: mu)
z_recon = self.reparam(mu, logvar) if self.training else mu
h0 = self.latent_to_hidden(z_recon).unsqueeze(0) # [1,B,H]
# 教師強制
dec_inp_ids = x[:, :-1] # 入力
dec_tgt_ids = x[:, 1:] # 教師
# word dropout(学習時のみ; pad/end/startは保護)
if self.training and word_dropout_p > 0:
keep_mask = (dec_inp_ids != pad_idx) & (dec_inp_ids != end_idx) & (dec_inp_ids != start_idx)
drop_rand = torch.rand_like(dec_inp_ids.float())
drop_mask = (drop_rand < word_dropout_p) & keep_mask
dec_inp_ids = dec_inp_ids.masked_fill(drop_mask, pad_idx)
dec_inp = self.embed(dec_inp_ids)
dec_out, _ = self.decoder_rnn(dec_inp, h0)
logits = self.fc_out(dec_out) # [B, T-1, V]
# 回帰は決定論的な z(=mu)で安定化(設定で切替可)
y_pred = None
if y_targets is not None:
z_pred = mu if deterministic_pred else z_recon
y_pred = self.predict_target(z_pred)
return logits, dec_tgt_ids, mu, logvar, y_pred
@torch.no_grad()
def sample(self, z, max_len=None, p=0.9, temperature=1.0, use_topp=False, forbid_unk=True):
if max_len is None:
max_len = self.max_len
h = self.latent_to_hidden(z).unsqueeze(0) # [1,B,H]
B = z.size(0)
cur = torch.full((B, 1), start_idx, dtype=torch.long, device=z.device)
cur_emb = self.embed(cur)
out_ids = []
for _ in range(max_len - 1):
dec_out, h = self.decoder_rnn(cur_emb, h) # [B,1,H]
logits = self.fc_out(dec_out).squeeze(1) # [B,V]
# 温度
if temperature != 1.0:
logits = logits / temperature
# 禁止トークン
if forbid_unk:
logits[:, unk_idx] = float('-inf')
logits[:, pad_idx] = float('-inf')
logits[:, start_idx] = float('-inf')
if use_topp:
next_id = sample_top_p(logits, p=p, temperature=1.0).unsqueeze(1) # [B,1]
else:
next_id = logits.argmax(-1, keepdim=True) # [B,1]
out_ids.append(next_id)
if (next_id == end_idx).all():
break
cur_emb = self.embed(next_id)
return torch.cat(out_ids, dim=1) if out_ids else cur
まずは、コンストラクタの中を説明していきます。
-
Embedding層:SELFIESトークンID(整数)を連続ベクトル表現(埋め込み)に変換、各トークンを
hidden次元のベクトルに写像します。
self.embed = nn.Embedding(vocab_size, hidden, padding_idx=pad_idx)
-
Encoder:GRUでSELFIESの系列を読み込み、最終隠れ状態から
μ(平均)、logvar(対数分散)を計算します
self.encoder_rnn = nn.GRU(hidden, hidden, batch_first=True)
self.mu = nn.Linear(hidden, latent)
self.logvar = nn.Linear(hidden, latent)
-
Decoder:潜在ベクトル
zをhiddenに戻して、GRUの初期状態に変換、GRUでSELFIESを1トークンずつ生成し、最後にfc_outで各トークンのlogits(確率スコア)に変換します。
self.decoder_rnn = nn.GRU(hidden, hidden, batch_first=True)
self.fc_out = nn.Linear(hidden, vocab_size)
self.latent_to_hidden = nn.Linear(latent, hidden)
logitsは各トークンが次に出る傾向(スコア)を表す生の値で、softmaxをかけると確率分布になります。
例として、
logits =
[C] → 3.2
[N] → 1.0
[O] → -2.5
softmaxをかけると、
[C] → 0.87
[N] → 0.12
[O] → 0.01
みたいな感じです。実際の実装では、logitsのまま、cross_entropyに入力して、誤差を出します。これは、PyTorchのF.cross_entropy()は内部でsoftmaxを使うためです。
-
ターゲット回帰ヘッド:潜在ベクトル
zから、logP/qed/sasなどの単一スカラーを予測するMLPです。
self.target_regressor = nn.Sequential(
nn.Linear(latent, hidden),
nn.ReLU(),
nn.Dropout(0.3),
nn.Linear(hidden, hidden // 2),
nn.ReLU(),
nn.Dropout(0.3),
nn.Linear(hidden // 2, hidden // 4),
nn.ReLU(),
nn.Dropout(0.2),
nn.Linear(hidden // 4, 1)
)
次にメソッドを説明していきます
-
encode:SELFIES系列をGRUに通して、分子全体を表す特徴ベクトル
hを取得、そこからμ、logvarを計算し、潜在分布を決めます。
def encode(self, x):
x_emb = self.embed(x) # [B,T,H]
_, h = self.encoder_rnn(x_emb) # [1,B,H]
h = h[-1] # [B,H]
return self.mu(h), self.logvar(h)
-
reparam:
reparameterizarion trickの部分、z = μ + σ ⊙ εとして、微分可能なサンプリングを実現します。
def reparam(self, mu, logvar):
eps = torch.randn_like(mu)
return mu + eps * (0.5 * logvar).exp()
-
predict_target:潜在ベクトル
zをMLPに通して、選択したターゲットの予測値を出します。
def predict_target(self, z):
out = self.target_regressor(z)
return out.squeeze(-1)
-
sample:潜在ベクトル
zからSELFIES系列を自動生成します。startトークンから初めて、GRUデコーダで1ステップずつトークンをサンプリングします。use_topp=Trueの場合は、top-pサンプリングを用いて「そこそこ多様で、そこそこ品質の良い」分子を生成します。また、<unk>,<pad>,<start>を生成禁止にしているので、変なトークンが出ないようになっています。
@torch.no_grad()
def sample(self, z, max_len=None, p=0.9, temperature=1.0, use_topp=False, forbid_unk=True):
...
最後に損失関数を定義して終わりです。この関数は、VAEを「生成モデル+物性回帰モデル」として、同時に学習させるための複合損失になります。
# Loss function with generic single-target regression (e.g., logP / qed / SAS)
def vae_loss_with_regression(
logits, tgt_ids, mu, logvar, y_pred, y_targets,
beta=1.0, reg_weight=0.1, tau=0.5, weight=None,
label_smoothing=0.1, target_mean=None, target_std=None
):
"""
3つの損失を統合:
1) 再構成誤差(CE): 分子の自己回帰再構成
2) KL損失(free-bits τ): 潜在分布の正則化
3) 回帰損失(MSE): 任意ターゲット(logP / qed / SAS 等)
期待スケール:
- y_pred は標準化スケール(mean/stdでのzスコア)を出す前提
- y_targets はここで (y - mean)/std に正規化する
- target_mean と target_std は必須(trainセットから算出した値)
"""
B, Tm1, V = logits.size()
# 1) Reconstruction loss
rec = F.cross_entropy(
logits.reshape(B * Tm1, V),
tgt_ids.reshape(B * Tm1),
ignore_index=pad_idx,
weight=weight,
label_smoothing=label_smoothing
)
# 2) KL loss with free-bits
# kld_raw: [B, latent_dim]
kld_raw = -0.5 * (1 + logvar - mu.pow(2) - logvar.exp())
# free-bits: 各次元ごとにmin τで下駄。平均化でスカラーへ。
kld_fb = torch.clamp(kld_raw, min=tau).mean()
# 3) Regression loss (MSE on normalized scale)
if (y_pred is not None) and (y_targets is not None):
assert target_mean is not None and target_std is not None, \
"target_mean/target_std を指定してください(trainから算出した値)"
y_targets_norm = (y_targets - target_mean) / target_std
reg_loss = F.mse_loss(y_pred, y_targets_norm)
else:
reg_loss = torch.tensor(0.0, device=logits.device)
# Total
total_loss = rec + beta * kld_fb + reg_weight * reg_loss
return total_loss, rec, kld_fb, reg_loss
再構成は「どれだけ元の分子に近い SELFIES を生成できるか」、
KL は「潜在空間 z を正規分布に寄せて生成能力を高める」、
回帰は「logP/QED/SAS をどれだけ精度よく予測できるか」を意味します。
これらをバランスよく学習させることで、生成と物性予測を内部で同時に学習する強力な VAE を作ることができます。
色々定義が長くなりました。お疲れ様です、一回休憩しましょう☕
VAE学習・評価
それでは、今まで定義してきた諸々を使って、VAEを学習させていきます。
print(f"=== Training VAE with {target} regression ===")
# Training settings
USE_ANNEAL = True # βをエポックで線形に上げる
tau = 0.75 # free-bits floor
reg_weight = 0.2 # 回帰ロスの重み
epochs = 200
kl_warmup_epochs = 30
clip_grad = 1.0
# end_idxが未定義でも落ちないように安全に扱う
try:
_end_idx = end_idx
except NameError:
_end_idx = None
# モデル定義
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model_with_reg = SelfiesVAEWithRegressor(
vocab_size=len(tokens),
hidden=256,
latent=64,
max_len=max_len,
target_mean=y_mean, # ← trainから計算した平均
target_std=y_std # ← trainから計算した標準偏差
).to(device)
opt_reg = torch.optim.Adam(model_with_reg.parameters(), lr=1e-3)
# 出力トークン重み(例:<end>を少し重く)
weight = torch.ones(len(tokens), device=device)
if (_end_idx is not None) and (0 <= _end_idx < len(tokens)):
weight[_end_idx] = 1.3
history_reg = {
"epoch": [], "loss": [], "rec": [], "kld_eff": [], "kld_raw": [],
"reg_loss": [], f"{target}_mae": [], f"val_{target}_mae": [], "val_rec": []
}
for epoch in range(1, epochs + 1):
model_with_reg.train()
# KL annealing
beta = min(1.0, epoch / kl_warmup_epochs) if USE_ANNEAL else 1.0
sum_loss = 0.0
sum_rec = 0.0
sum_kld_eff = 0.0
sum_kld_raw = 0.0
sum_reg = 0.0
# MAE はサンプル数で加重平均
sum_mae_abs = 0.0
n_batches = 0
n_samples = 0
for batch_data, batch_y in tqdm(train_loader, leave=False):
batch_data = batch_data.to(device, non_blocking=True)
batch_y = batch_y.to(device, non_blocking=True)
logits, tgt_ids, mu, logvar, y_pred = model_with_reg(batch_data, y_targets=batch_y)
# 損失計算(標準化は関数内で実施)
loss, rec, kld_eff, reg_loss = vae_loss_with_regression(
logits, tgt_ids, mu, logvar, y_pred, batch_y,
beta=beta, reg_weight=reg_weight, tau=tau, weight=weight,
target_mean=model_with_reg.target_mean, target_std=model_with_reg.target_std
)
# 監視用:raw-KL と “元スケール” MAE(サンプル加重)
with torch.no_grad():
kld_raw = -0.5 * (1 + logvar - mu.pow(2) - logvar.exp()).mean()
y_pred_denorm = y_pred * model_with_reg.target_std + model_with_reg.target_mean
sum_mae_abs += F.l1_loss(y_pred_denorm, batch_y, reduction='sum').item()
opt_reg.zero_grad(set_to_none=True)
loss.backward()
nn.utils.clip_grad_norm_(model_with_reg.parameters(), clip_grad)
opt_reg.step()
# 集計
bsz = batch_data.size(0)
n_samples += bsz
n_batches += 1
sum_loss += loss.item()
sum_rec += rec.item()
sum_kld_eff += kld_eff.item()
sum_kld_raw += kld_raw.item()
sum_reg += reg_loss.item()
# 平均化
avg_loss = sum_loss / max(1, n_batches)
avg_rec = sum_rec / max(1, n_batches)
avg_kld_eff = sum_kld_eff / max(1, n_batches)
avg_kld_raw = sum_kld_raw / max(1, n_batches)
avg_reg = sum_reg / max(1, n_batches)
avg_mae = (sum_mae_abs / max(1, n_samples)) # 元スケールでのMAE
# ---- Validation(target MAE と 再構成loss)----
model_with_reg.eval()
val_sum_mae_abs = 0.0
val_n_samples = 0
val_sum_rec = 0.0
val_n_batches = 0
with torch.no_grad():
for batch_data, batch_y in val_loader:
batch_data = batch_data.to(device, non_blocking=True)
batch_y = batch_y.to(device, non_blocking=True)
logits, tgt_ids, mu, logvar, y_pred = model_with_reg(batch_data, y_targets=batch_y)
# 再構成lossのみ(βや回帰は評価指標から外すことが多い)
rec_only, _, _, _ = vae_loss_with_regression(
logits, tgt_ids, mu, logvar, y_pred, batch_y,
beta=0.0, reg_weight=0.0, tau=tau, weight=weight,
target_mean=model_with_reg.target_mean, target_std=model_with_reg.target_std
)
y_pred_denorm = y_pred * model_with_reg.target_std + model_with_reg.target_mean
val_sum_mae_abs += F.l1_loss(y_pred_denorm, batch_y, reduction='sum').item()
val_sum_rec += rec_only.item()
val_n_batches += 1
val_n_samples += batch_data.size(0)
val_mae = val_sum_mae_abs / max(1, val_n_samples)
val_rec = val_sum_rec / max(1, val_n_batches)
# 記録
history_reg["epoch"].append(epoch)
history_reg["loss"].append(avg_loss)
history_reg["rec"].append(avg_rec)
history_reg["kld_eff"].append(avg_kld_eff)
history_reg["kld_raw"].append(avg_kld_raw)
history_reg["reg_loss"].append(avg_reg)
history_reg[f"{target}_mae"].append(avg_mae)
history_reg[f"val_{target}_mae"].append(val_mae)
history_reg["val_rec"].append(val_rec)
# ログ
if (epoch % 10) == 0 or epoch == 1:
print(
f"Epoch {epoch:03d} | beta={beta:.2f} | reg_w={reg_weight:.2f} | "
f"loss={avg_loss:.3f} | rec={avg_rec:.3f} | kld={avg_kld_eff:.3f} | "
f"reg={avg_reg:.3f} | {target}_MAE(train)={avg_mae:.4f} | "
f"{target}_MAE(val)={val_mae:.4f}"
)
print("Training completed!")
何をしているのか、順に説明していくと、
1⃣ 学習設定とモデルの設定
print(f"=== Training VAE with {target} regression ===")
USE_ANNEAL = True # βをエポックで線形に上げる
tau = 0.75 # free-bits floor
reg_weight = 0.2 # 回帰ロスの重み
epochs = 200
kl_warmup_epochs = 30
clip_grad = 1.0
- β-annealing:最初はKLを弱めて、再構成にしゅうちゅう、そこから徐々にKLを効かせていく
- tau:KL free-bitsの下限値設定、VAE崩壊を防ぐためのハイパラ。posterior collapse対策
- reg_weight :物性回帰の損失をどこまで重視するか
- clip_grad:勾配クリッピングで学習を安定化
2⃣ 学習履歴を記録する辞書を用意
history_reg = {
"epoch": [], "loss": [], "rec": [], "kld_eff": [], "kld_raw": [],
"reg_loss": [], f"{target}_mae": [], f"val_{target}_mae": [], "val_rec": []
}
3⃣ エポックループでミニバッチ毎に学習
for epoch in range(1, epochs + 1):
model_with_reg.train()
beta = min(1.0, epoch / kl_warmup_epochs) if USE_ANNEAL else 1.0
β-annealing:最初の 30 epoch で KL の重みを 0 → 1 に線形に増加
for batch_data, batch_y in tqdm(train_loader, leave=False):
batch_data = batch_data.to(device, non_blocking=True)
batch_y = batch_y.to(device, non_blocking=True)
logits, tgt_ids, mu, logvar, y_pred = model_with_reg(batch_data, y_targets=batch_y)
- logits : 次トークン予測用のロジット
- tgt_ids : 教師のトークンID列
- mu, logvar : 潜在分布パラメータ
- y_pred : 標準化スケールの物性予測を得る
loss, rec, kld_eff, reg_loss = vae_loss_with_regression(
logits, tgt_ids, mu, logvar, y_pred, batch_y,
beta=beta, reg_weight=reg_weight, tau=tau, weight=weight,
target_mean=model_with_reg.target_mean, target_std=model_with_reg.target_std
)
先の損失関数を呼び出し、以下を取得
- total_loss : 最適化に使う
- rec : 再構成誤差
- kld_eff : free-bits適用後のKL
- reg_loss : 回帰MSE
with torch.no_grad():
kld_raw = -0.5 * (1 + logvar - mu.pow(2) - logvar.exp()).mean()
y_pred_denorm = y_pred * model_with_reg.target_std + model_with_reg.target_mean
sum_mae_abs += F.l1_loss(y_pred_denorm, batch_y, reduction='sum').item()
モニタリング用に、rawのKL(free_bits適用前)と元スケールでのMAEを集計
opt_reg.zero_grad(set_to_none=True)
loss.backward()
nn.utils.clip_grad_norm_(model_with_reg.parameters(), clip_grad)
opt_reg.step()
いつものPyTorch学習ステップ、勾配初期化→逆伝播→勾配クリッピング→パラメータ更新です。
4⃣ エポックごとに平均値計算
avg_loss = sum_loss / max(1, n_batches)
...
avg_mae = sum_mae_abs / max(1, n_samples)
ここで、trainの統計値が出ます。
5⃣ 検証での評価
model_with_reg.eval()
with torch.no_grad():
for batch_data, batch_y in val_loader:
...
rec_only, _, _, _ = vae_loss_with_regression(
logits, tgt_ids, mu, logvar, y_pred, batch_y,
beta=0.0, reg_weight=0.0, ...
)
...
val_sum_mae_abs += F.l1_loss(y_pred_denorm, batch_y, reduction='sum').item()
検証では、再構成誤差(CE)のみを評価指標として使い、元スケールでのtarget MAEも測定しています。
val_mae = val_sum_mae_abs / max(1, val_n_samples)
val_rec = val_sum_rec / max(1, val_n_batches)
てな感じです。学習が終わったら、結果を可視化してみます。
# === Visualization (generic target: logP / qed / SAS etc.) ===
epochs = history_reg["epoch"]
train_key = f"{target}_mae"
val_key = f"val_{target}_mae"
# 軸ラベル(単位系の目安)
ylab_map = {
"logP": "MAE (logP)",
"qed": "MAE (QED)",
"sas": "MAE (SAS score)",
"SAS": "MAE (SAS score)",
}
y_label = ylab_map.get(target, f"MAE ({target})")
# タイトル整形
title_target = target.upper()
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
# (1) Training losses
ax = axes[0]
ax.plot(epochs, history_reg["loss"], label="Total Loss")
ax.plot(epochs, history_reg["rec"], label="Reconstruction")
ax.plot(epochs, history_reg["kld_eff"], label="KL (effective)")
ax.plot(epochs, history_reg["reg_loss"], label="Regression")
ax.set_xlabel("Epoch"); ax.set_ylabel("Loss"); ax.set_title("Training Losses")
ax.legend()
# (2) KL
ax = axes[1]
ax.plot(epochs, history_reg["kld_eff"], label="KL (effective)")
ax.plot(epochs, history_reg["kld_raw"], label="KL (raw)", linestyle="--")
ax.set_xlabel("Epoch"); ax.set_ylabel("KL Divergence"); ax.set_title("KL Divergence")
ax.legend()
# (3) Target MAE (train / val)
ax = axes[2]
ax.plot(epochs, history_reg[train_key], label=f"{title_target} MAE (train)")
ax.plot(epochs, history_reg[val_key], label=f"{title_target} MAE (val)")
ax.set_xlabel("Epoch"); ax.set_ylabel(y_label); ax.set_title(f"{title_target} Prediction Error")
ax.legend()
plt.tight_layout()
plt.show()
final_mae = history_reg[train_key][-1]
print(f"Final {title_target} MAE (train): {final_mae:.4f}")
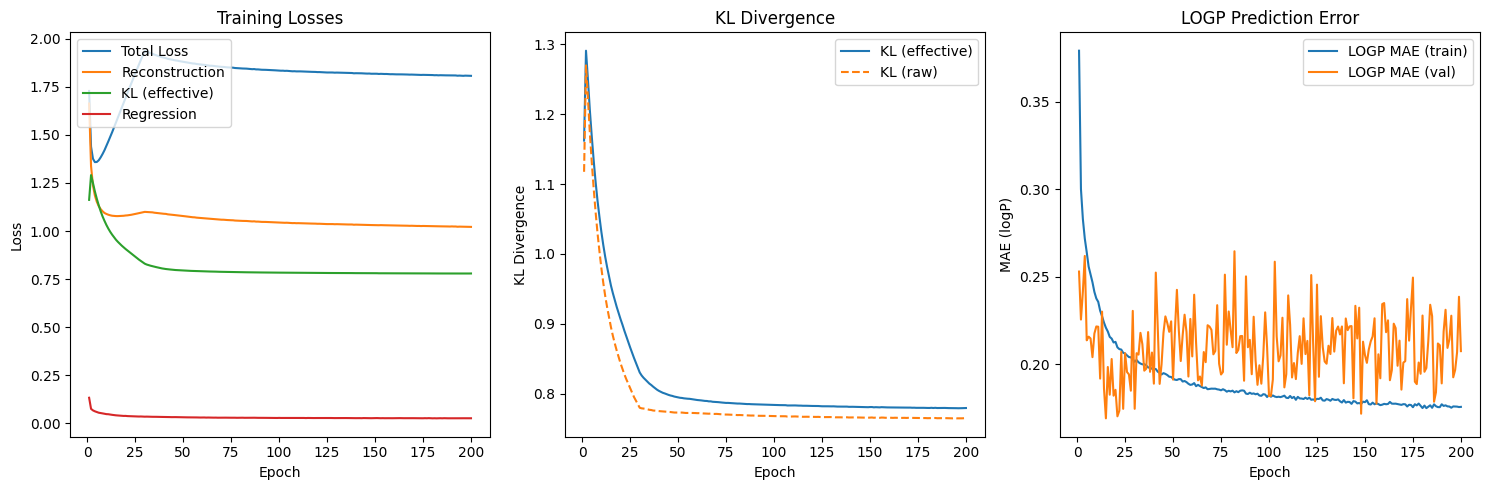
損失の推移を見ていくと、まず左図は損失を示しており、
- Reconstruction : 1.75→1.0くらいまで減少
- Regression : 0.15→0.03くらいまですっと下がって頭打ち
- KL(effective) : 1.25→0.78くらいまで下がって安定
- total loss : 途中から上がっているが、Βがwarm upで0→1に上がることが原因で、KL項が効いてくるため
⇒再構成誤差、回帰誤差、KLすべて減少し、落ち着いている
中央図からは、KL(raw)/KL(eff)ともにスムーズに減少し、0近くに潰れていないので、posterior collapse(auto encoderになってしまうこと)は起こっていない
右図はlogP MAEグラフで、trainは単調減少し、valの方は揺らぎながらほぼ水平となっており、発散はしていない。
以上を踏まえて、ある程度問題なく学習が完了していることが分かります!!
新しい分子の生成・予測
それではVAEの学習が終わったので、本命の新しい分子生成を行いましょう。ただ、分子をたくさん生成しても、それらが目的の指標から大きく外れるものだと、無駄な分子がたくさん出てきてしまい煩雑になってしまいます。そこで事前に基準のようなものを設けておいて、その基準で生成分子をフィルタリングし、有望な分子のみを選定していきます。
下記のコードがフィルタリングの関数です。薬に関しては素人なので、チャッピーに作ってもらいました。
# ドラッグライク判定フィルタ
from rdkit import Chem
from rdkit.Chem import QED, Descriptors, rdMolDescriptors, FilterCatalog
# ---- PAINS / Brenk カタログ用意 ----
def _build_alert_catalog():
params = FilterCatalog.FilterCatalogParams()
# PAINS と Brenk をまとめて有効化(A/B/C全系を含む)
params.AddCatalog(FilterCatalog.FilterCatalogParams.FilterCatalogs.PAINS)
params.AddCatalog(FilterCatalog.FilterCatalogParams.FilterCatalogs.BRENK)
return FilterCatalog.FilterCatalog(params)
_ALERT_CATALOG = _build_alert_catalog()
# ---- SASスコア:モジュールがあれば使う、無ければ None を返す ----
def try_calc_sas(mol):
try:
from rdkit.Chem import rdMolDescriptors as rdm
# sascorer は RDKit本体に同梱されないことがあるため try-import
import sascorer # もし無ければ pip/ファイル設置が必要
return float(sascorer.calculateScore(mol))
except Exception:
return None # 取れなくてもフィルタは通す(SAS条件はスキップ)
def ok_druglike_molecule(
m,
mw_max=500.0,
logp_max=5.0,
hbd_max=5,
hba_max=10,
tpsa_max=140.0,
rotb_max=10,
qed_min=0.4, # 目安: 0.4〜0.9 が多い
sas_max=6.5, # 目安: <=6〜7 程度
enforce_alerts=True
):
"""
ZINC/創薬向けの簡易フィルタ:
- RDKitサニタイズ
- Lipinski(Ro5)
- Veber(TPSA, RotB)
- QED 下限
- (あれば)SAS 上限
- PAINS / Brenk alerts の除外
"""
try:
Chem.SanitizeMol(m)
except Exception:
return False
# 元素制限は緩め(ZINCは広い): 少なくともメインチャネルが有機
atom_symbols = {a.GetSymbol() for a in m.GetAtoms()}
if not any(sym in atom_symbols for sym in ("C", "N", "O")):
return False
mw = Descriptors.MolWt(m)
logp = Descriptors.MolLogP(m)
hbd = rdMolDescriptors.CalcNumHBD(m)
hba = rdMolDescriptors.CalcNumHBA(m)
tpsa = rdMolDescriptors.CalcTPSA(m)
rotb = rdMolDescriptors.CalcNumRotatableBonds(m)
qed_v = QED.qed(m)
if mw > mw_max or logp > logp_max or hbd > hbd_max or hba > hba_max:
return False
if tpsa > tpsa_max or rotb > rotb_max:
return False
if qed_v < qed_min:
return False
sas = try_calc_sas(m)
if (sas is not None) and (sas > sas_max):
return False
if enforce_alerts and _ALERT_CATALOG.GetFirstMatch(m) is not None:
# PAINS/Brenk に引っかかったら除外
return False
return True
def normalize_generated_selfies(selfies_str):
"""
Normalize generated SELFIES to ensure uniqueness
生成した SELFIES を正規化してから再エンコードする関数。
モデルが同じ分子を別表記で何個も出すのを防いで、ユニーク度管理をしやすくする。
decoder による一旦の SMILES 化で RDKit の検証を通す → 不正構造を弾ける。
"""
try:
smiles = sf.decoder(selfies_str)
mol = Chem.MolFromSmiles(smiles)
if mol is None:
return None
canonical_smiles = Chem.MolToSmiles(mol, canonical=True)
return sf.encoder(canonical_smiles)
except:
return None
ざっくり説明すると、生成した SELFIES から drug-like な分子だけを残すために、
- Lipinski / Veber / QED / SAS / PAINS / Brenk などの基本的な創薬フィルタを一括で適用
- さらに、生成された SELFIES は一度 SMILES に戻して RDKit で構造チェックを行い、canonical SMILES を経由して再び SELFIES に変換することで、同一分子が複数表記で重複する問題を防ぐ
とのことです。この辺はどういった分子を扱うかで、フィルタリングの条件が変わるかと思います。生成する分子が少ないのであれば、自らの経験・知識でフィルタリングするのもありかと思います。
前置きが長くなりましたが、いよいよ分子生成です![]()
# --- generation config ---
USE_NEIGHBOR = True
N_GEN = 100
noise_scale = 0.05
seed = 1234
USE_FILTER = True
g_gen = torch.Generator(device=device).manual_seed(seed)
# --- neighbor sampling ---
model_with_reg.eval()
with torch.no_grad():
if USE_NEIGHBOR:
# 潜在空間の平均μと平均σを格納するためのリスト
mu_list, std_list = [], []
seen = 0 # 処理したサンプル数のカウンタ
LIMIT = 1000 # データサンプルの上限数、全ての学習データを使うのではなく一部のデータの洗剤表現をプールしておく
for batch_data, _ in train_loader:
batch_data = batch_data.to(device)
mu, logvar = model_with_reg.encode(batch_data)
std = (0.5 * logvar).exp()
mu_list.append(mu)
std_list.append(std)
seen += batch_data.size(0)
if seen >= LIMIT:
break
# 先の収集した平均μと平均σのプールから新しいzベクトルの生成
if mu_list:
# リストに格納されたμ、σのテンソルを結合し、洗剤統計情報のプール(bank)を作成
mu_bank = torch.cat(mu_list, 0)
std_bank = torch.cat(std_list, 0)
# プール内の全データから、N_GEN個のインデックスをランダムに選択
idx = torch.randint(mu_bank.size(0), (N_GEN,), device=device, generator=g_gen)
# 選ばれたインデックスに対応するμとσを取得する。これが新しいzベクトルの基礎となる
z_base = mu_bank[idx]
z_std = std_bank[idx]
# 標準正規分布からランダムノイズをサンプリングする
eps = torch.randn(z_base.shape, device=z_base.device, generator=g_gen)
# 近傍サンプリングを実施
z = z_base + noise_scale * z_std * eps
print(f"[Neighbor sampling] Generated {N_GEN} z vectors (pool={seen})")
else:
z = torch.randn(N_GEN, model_with_reg.latent, device=device, generator=g_gen)
print("[Fallback→Random]")
else:
z = torch.randn(N_GEN, model_with_reg.latent, device=device, generator=g_gen)
print(f"[Random sampling] Generated {N_GEN} z vectors")
# --- decode to SELFIES ---
with torch.no_grad():
gen_ids_batch = model_with_reg.sample(z, p=0.75, temperature=0.6, use_topp=True)
# --- SELFIES→SMILES→Mol ---
mols, smiles_list, selfies_list_gen = [], [], []
for i in range(gen_ids_batch.size(0)):
gen_sfs = ids_to_selfies(gen_ids_batch[i].tolist())
normalized_sfs = normalize_generated_selfies(gen_sfs)
if normalized_sfs is None:
continue
try:
gen_smi = sf.decoder(normalized_sfs)
except Exception:
continue
mol = Chem.MolFromSmiles(gen_smi)
if mol is None:
continue
if USE_FILTER and not ok_druglike_molecule(mol):
continue
mols.append(mol)
smiles_list.append(gen_smi)
selfies_list_gen.append(normalized_sfs)
print(f"Valid molecules: {len(mols)}/{gen_ids_batch.size(0)}")
# --- predict target ---
@torch.no_grad()
def predict_target_from_selfies_list(model, sfs_list, max_len=120, tta_n=0, batch_size=256):
model.eval()
y_all = []
dev = next(model.parameters()).device
for i in range(0, len(sfs_list), batch_size):
chunk = sfs_list[i:i+batch_size]
ids = [encode_selfies(s, max_len=max_len) for s in chunk]
x = torch.tensor(ids, dtype=torch.long, device=dev)
if tta_n > 0:
preds = []
for _ in range(tta_n):
_, _, mu, logvar, y_pred = model(
x, y_targets=torch.zeros(x.size(0), device=dev),
deterministic_pred=False
)
preds.append(y_pred)
y_norm = torch.stack(preds).mean(0)
else:
_, _, mu, logvar, y_pred = model(
x, y_targets=torch.zeros(x.size(0), device=dev),
deterministic_pred=True
)
y_norm = y_pred
y = y_norm * model.target_std + model.target_mean
y_all.extend(y.detach().cpu().tolist())
return y_all
target_preds = predict_target_from_selfies_list(model_with_reg, selfies_list_gen, max_len=max_len, tta_n=0)
# ===== Display =====
if mols:
print(f"Generated {len(mols)} valid molecules")
# ラベル・単位のマッピング
label_map = {
"logP": ("Predicted logP", "{v:.2f}"),
"qed": ("Predicted QED", "{v:.3f}"),
"SAS": ("Predicted SAS", "{v:.2f}"),
"sas": ("Predicted SAS", "{v:.2f}"),
}
y_title, fmt = label_map.get(target, (f"Predicted {target}", "{v:.3f}"))
legends = [f"{y_title.split()[-1]}: " + fmt.format(v=v) for v in target_preds]
img = Draw.MolsToGridImage(mols, molsPerRow=5, subImgSize=(200, 200), legends=legends)
display(img)
plt.figure(figsize=(8, 4))
plt.hist(target_preds, bins=15, alpha=0.7, edgecolor='black')
plt.xlabel(y_title)
plt.ylabel('Count')
plt.title(f'Distribution of {y_title}')
mu = float(np.mean(target_preds)) if len(target_preds) else float("nan")
plt.axvline(mu, linestyle='--', label=f'Mean: {fmt.format(v=mu)}')
plt.legend()
plt.show()
if target.lower() == "logp":
print(f"logP range: {min(target_preds):.2f} .. {max(target_preds):.2f}")
elif target.lower() == "qed":
print(f"QED range: {min(target_preds):.3f} .. {max(target_preds):.3f}")
else:
print(f"{target} range: {min(target_preds):.3f} .. {max(target_preds):.3f}")
[Neighbor sampling] Generated 100 z vectors (pool=1024)
Valid molecules: 73/100
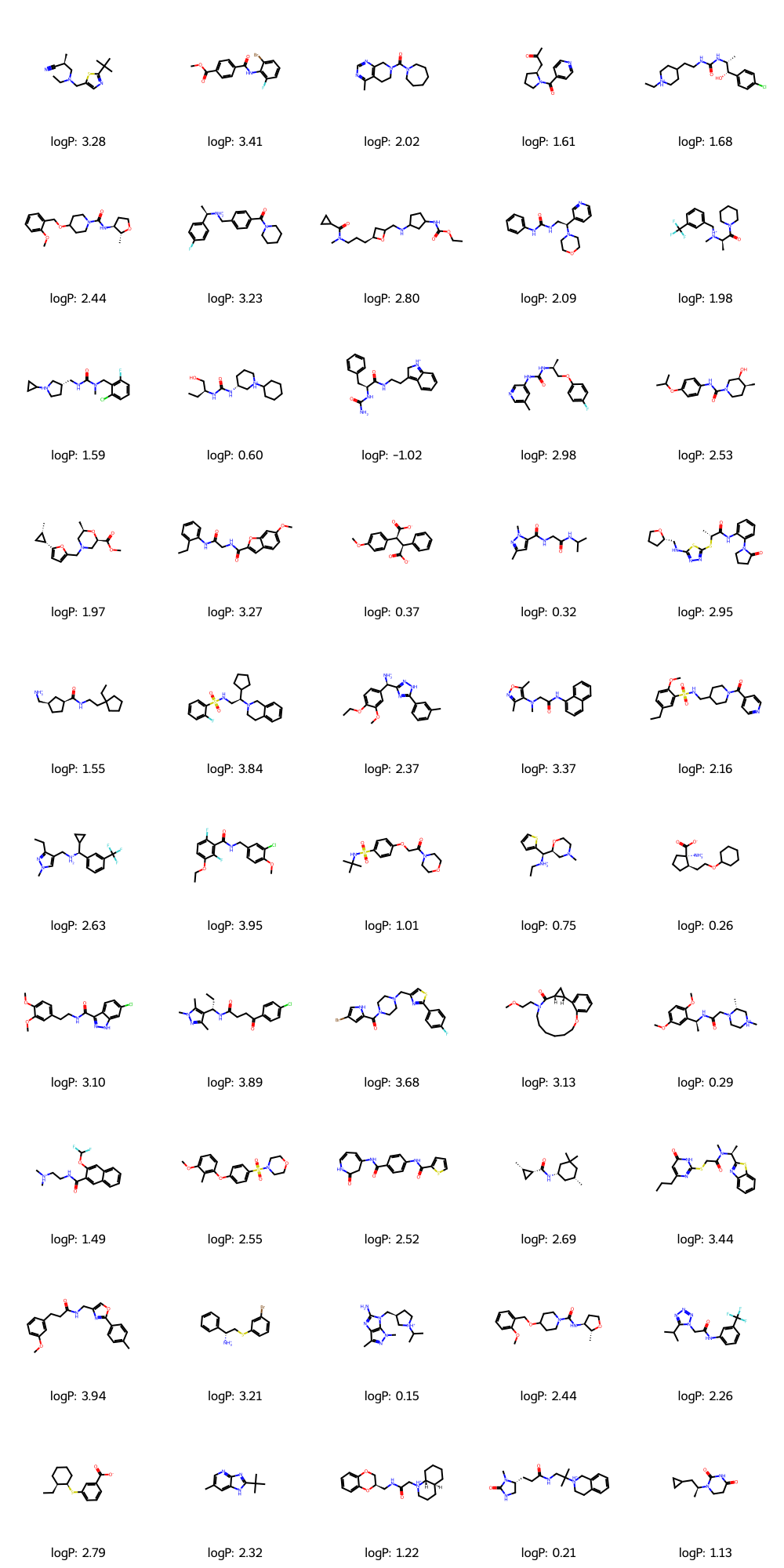
Generated 73 valid molecules
新しい分子が生成され、予測されたlogPの値が記載されています!!
100分子のうち有効な分子は73分子でした。中にはおかしな構造を持つ分子が混ざっていますが、おおむね問題なさそうです。
コードの中身を説明していきます。
① 生成設定と乱数
USE_NEIGHBOR = True
N_GEN = 100
noise_scale = 0.05
seed = 1234
USE_FILTER = True
g_gen = torch.Generator(device=device).manual_seed(seed)
-
USE_NEIGHBOR: 学習済み分子の近傍からzをサンプリングするneighbor samplingを使うかどうか -
N_GEN: 潜在ベクトルzをいくつ生成するか -
noise_scale: 近傍にどれだけ揺らぎを加えるか -
seed: 乱数シードで再現性確保 -
USE_FILTER: 先ほど定義したok_druglike_moleculeでdrug-likeフィルターを使うかどうか
② 潜在空間からzをサンプリング (neighbor sampling)
model_with_reg.eval()
with torch.no_grad():
if USE_NEIGHBOR:
# 潜在空間の平均μと平均σを格納するためのリスト
mu_list, std_list = [], []
seen = 0 # 処理したサンプル数のカウンタ
LIMIT = 1000 # データサンプルの上限数、全ての学習データを使うのではなく一部のデータの洗剤表現をプールしておく
for batch_data, _ in train_loader:
batch_data = batch_data.to(device)
mu, logvar = model_with_reg.encode(batch_data)
std = (0.5 * logvar).exp()
mu_list.append(mu)
std_list.append(std)
seen += batch_data.size(0)
if seen >= LIMIT:
break
# 先の収集した平均μと平均σのプールから新しいzベクトルの生成
if mu_list:
# リストに格納されたμ、σのテンソルを結合し、洗剤統計情報のプール(bank)を作成
mu_bank = torch.cat(mu_list, 0)
std_bank = torch.cat(std_list, 0)
# プール内の全データから、N_GEN個のインデックスをランダムに選択
idx = torch.randint(mu_bank.size(0), (N_GEN,), device=device, generator=g_gen)
# 選ばれたインデックスに対応するμとσを取得する。これが新しいzベクトルの基礎となる
z_base = mu_bank[idx]
z_std = std_bank[idx]
# 標準正規分布からランダムノイズをサンプリングする
eps = torch.randn(z_base.shape, device=z_base.device, generator=g_gen)
# 近傍サンプリングを実施
z = z_base + noise_scale * z_std * eps
print(f"[Neighbor sampling] Generated {N_GEN} z vectors (pool={seen})")
else:
z = torch.randn(N_GEN, model_with_reg.latent, device=device, generator=g_gen)
print("[Fallback→Random]")
else:
z = torch.randn(N_GEN, model_with_reg.latent, device=device, generator=g_gen)
print(f"[Random sampling] Generated {N_GEN} z vectors")
ここでは、trainデータをエンコードして、各分子のμとσを集めておき、その中から、N_GEN個をランダムに選んでいます。
③ z → SELFIESへのデコード
with torch.no_grad():
gen_ids_batch = model_with_reg.sample(z, p=0.75, temperature=0.6, use_topp=True)
VAEのデコーダを使って、潜在ベクトルzからSELFIESのトークン列(ID列)を生成しています。各引数の設定により、top-pサンプリングでそこそこ多様、且つ、温度を下げて暴れすぎないようにしています。
④ SELFIES → SMILES → Mol + drug-like フィルタ
mols, smiles_list, selfies_list_gen = [], [], []
for i in range(gen_ids_batch.size(0)):
gen_sfs = ids_to_selfies(gen_ids_batch[i].tolist())
normalized_sfs = normalize_generated_selfies(gen_sfs)
if normalized_sfs is None:
continue
try:
gen_smi = sf.decoder(normalized_sfs)
except Exception:
continue
mol = Chem.MolFromSmiles(gen_smi)
if mol is None:
continue
if USE_FILTER and not ok_druglike_molecule(mol):
continue
mols.append(mol)
smiles_list.append(gen_smi)
selfies_list_gen.append(normalized_sfs)
手順として、序盤で定義したids_to_selfies関数により、ID列をSELFIES文字列に変換し、normalize_generated_selfies関数で、SELFIES → SMILES → RDKit Mol → canonical SMILES → SELFIES と変換させていきます。これにより、無効構造や重複構造を避けて、同じ分子は同じSELFIESで統一されます。
そして、SELFIES → SMILES → Molに変換し、RDkit Molに変換できないものは省いています。
最後に、ok_druglike_molecule関数を使って、薬らしい分子のみが生き残り、molsに格納されていきます。
⑤ 生成分子のターゲット値を予測
@torch.no_grad()
def predict_target_from_selfies_list(model, sfs_list, max_len=120, tta_n=0, batch_size=256):
model.eval()
y_all = []
dev = next(model.parameters()).device
for i in range(0, len(sfs_list), batch_size):
chunk = sfs_list[i:i+batch_size]
ids = [encode_selfies(s, max_len=max_len) for s in chunk]
x = torch.tensor(ids, dtype=torch.long, device=dev)
if tta_n > 0:
preds = []
for _ in range(tta_n):
_, _, mu, logvar, y_pred = model(
x, y_targets=torch.zeros(x.size(0), device=dev),
deterministic_pred=False
)
preds.append(y_pred)
y_norm = torch.stack(preds).mean(0)
else:
_, _, mu, logvar, y_pred = model(
x, y_targets=torch.zeros(x.size(0), device=dev),
deterministic_pred=True
)
y_norm = y_pred
y = y_norm * model.target_std + model.target_mean
y_all.extend(y.detach().cpu().tolist())
こちらは回帰部分の実装です。生成したSELFIESから再びencode_selfies関数でID列を作り、モデルに通して、目的変数の予測値を計算します。
y_predは標準化されているので、元のスケールに戻しています。
tta_n > 0にすると、deterministic_pred=Falseでzをサンプリングしつつ、複数回予測して平均として出力されます。ttaはtest-time augmentationの略です。
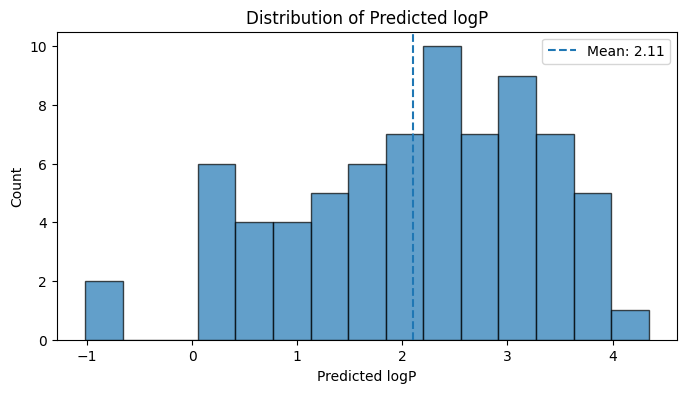
⑥ グリッド表示+ヒストグラム
if mols:
print(f"Generated {len(mols)} valid molecules")
label_map = { ... }
y_title, fmt = label_map.get(target, (f"Predicted {target}", "{v:.3f}"))
legends = [f"{y_title.split()[-1]}: " + fmt.format(v=v) for v in target_preds]
img = Draw.MolsToGridImage(mols, molsPerRow=5, subImgSize=(200, 200), legends=legends)
display(img)
plt.figure(figsize=(8, 4))
plt.hist(target_preds, bins=15, ...)
...
このコードにより、分子構造と一緒に予測された物性値が表示され、ヒストグラムに生成分子の物性分布が表示されます。今回はlogPのレンジがどの辺に集まっているかを可視化しています。
回帰ヘッド(MLP)の汎化性能評価
次に回帰ヘッドがうまく機能しているか見てみましょう。生成した分子に対して予測値が出力されましたが、そもそもその予測値が正しいかどうかわかりません。そこで、検証データを予測させ、汎化性能を見てみます。
# 回帰ヘッドの評価
print(f"=== Train & Validation Evaluation — target: {target} ===")
model_with_reg.eval()
train_true, train_pred = [], []
val_true, val_pred = [], []
with torch.no_grad():
# ---- Train ----
for batch_data, batch_y in train_loader:
batch_data = batch_data.to(device)
batch_y = batch_y.to(device)
# 決定論(z=μ)でターゲット予測
_, _, mu, logvar, y_pred = model_with_reg(
batch_data, y_targets=batch_y, deterministic_pred=True
)
# 逆正規化(モデルが保持する統計量を使用)
y_pred_denorm = y_pred * model_with_reg.target_std + model_with_reg.target_mean
train_true.extend(batch_y.cpu().numpy().tolist())
train_pred.extend(y_pred_denorm.cpu().numpy().tolist())
# ---- Validation ----
for batch_data, batch_y in val_loader:
batch_data = batch_data.to(device)
batch_y = batch_y.to(device)
_, _, mu, logvar, y_pred = model_with_reg(
batch_data, y_targets=batch_y, deterministic_pred=True
)
y_pred_denorm = y_pred * model_with_reg.target_std + model_with_reg.target_mean
val_true.extend(batch_y.cpu().numpy().tolist())
val_pred.extend(y_pred_denorm.cpu().numpy().tolist())
# メトリクス、学習・検証でそれぞれ計算
train_mae = mean_absolute_error(train_true, train_pred)
train_rmse = np.sqrt(mean_squared_error(train_true, train_pred))
train_r2 = r2_score(train_true, train_pred)
val_mae = mean_absolute_error(val_true, val_pred)
val_rmse = np.sqrt(mean_squared_error(val_true, val_pred))
val_r2 = r2_score(val_true, val_pred)
print(f"[Train] MAE={train_mae:.4f}, RMSE={train_rmse:.4f}, R²={train_r2:.3f}")
print(f"[Val ] MAE={val_mae:.4f}, RMSE={val_rmse:.4f}, R²={val_r2:.3f}")
print(f"Generalization gap (Val MAE - Train MAE): {val_mae - train_mae:.4f}")
# ターゲット別のラベル/単位
label_map = {
"logP": ("logP", ""),
"qed": ("QED", ""),
"QED": ("QED", ""),
"sas": ("SAS", ""),
"SAS": ("SAS", "")
}
ylab, unit = label_map.get(target, (target, ""))
unit_suffix = f" {unit}" if unit else ""
# 可視化
plt.figure(figsize=(15, 4))
# (1) Pred vs Actual (Train & Val)
plt.subplot(1, 3, 1)
plt.scatter(train_true, train_pred, alpha=0.5, label="Train", s=20)
plt.scatter(val_true, val_pred, alpha=0.7, label="Val", s=20)
lo = min(min(train_true + val_true), min(train_pred + val_pred))
hi = max(max(train_true + val_true), max(train_pred + val_pred))
plt.plot([lo, hi], [lo, hi], 'r--', lw=2)
plt.xlabel(f'Actual {ylab}{unit_suffix}')
plt.ylabel(f'Predicted {ylab}{unit_suffix}')
plt.title(f'Predicted vs Actual\nTrain R²={train_r2:.3f}, Val R²={val_r2:.3f}')
plt.legend()
# (2) Residuals (Train & Val)
plt.subplot(1, 3, 2)
train_res = np.array(train_pred) - np.array(train_true)
val_res = np.array(val_pred) - np.array(val_true)
plt.scatter(train_pred, train_res, alpha=0.5, label="Train", s=20)
plt.scatter(val_pred, val_res, alpha=0.7, label="Val", s=20)
plt.axhline(0, color='r', linestyle='--')
plt.xlabel(f'Predicted {ylab}{unit_suffix}')
plt.ylabel(f'Residual{unit_suffix}')
plt.title(f'Residuals\nTrain MAE={train_mae:.4f}, Val MAE={val_mae:.4f}')
plt.legend()
# (3) Distribution (Train & Val)
plt.subplot(1, 3, 3)
plt.hist(train_true, bins=20, alpha=0.5, label='Train True')
plt.hist(val_true, bins=20, alpha=0.5, label='Val True')
plt.xlabel(f'{ylab}{unit_suffix}')
plt.ylabel('Count')
plt.title('Target Distribution (True)')
plt.legend()
plt.tight_layout()
plt.show()
=== Train & Validation Evaluation — target: logP ===
[Train] MAE=0.1983, RMSE=0.2570, R²=0.968
[Val ] MAE=0.2074, RMSE=0.2748, R²=0.963
Generalization gap (Val MAE - Train MAE): 0.0090
検証データでも高い予測精度を示すことが分かりました。やはりデータセットのサイズは大事!! ただ、データ数の少ないlogPが低い領域と高い領域はやや予測を外しています。この辺はもう少しepoch数を増やすなどすれば改善できそうです。
モデルは一度保存しておきましょう、再度学習させるとかなり時間がかかるので。。。
# モデルの保存
os.makedirs("model", exist_ok=True)
save_path = "model/vae_regressor.pth"
torch.save({
"model_state": model_with_reg.state_dict(),
"vocab": tokens, # 語彙リスト
"stoi": stoi,
"itos": itos,
"max_len": max_len,
"target": target,
"target_mean": y_mean,
"target_std": y_std,
}, save_path)
print(f"Model saved to: {save_path}")
これで、modelというディレクトリにpth形式でモデルが保存されます。
ベンゼンを入力してみる
論文の図と同様にベンゼンを入力してみて、どんな分子が生成されるか見てみます。先ほど保存したモデルを読み込みましょう。
# モデル読み込み
checkpoint = torch.load("model/vae_regressor.pth", map_location=device)
# モデル構造は学習時と同じものを作る必要あり
loaded_model = SelfiesVAEWithRegressor(
vocab_size=len(checkpoint["vocab"]),
hidden=256,
latent=64,
max_len=checkpoint["max_len"],
target_mean=checkpoint["target_mean"],
target_std=checkpoint["target_std"],
).to(device)
loaded_model.load_state_dict(checkpoint["model_state"])
loaded_model.eval()
# 辞書類も復元
tokens = checkpoint["vocab"]
stoi = checkpoint["stoi"]
itos = checkpoint["itos"]
max_len = checkpoint["max_len"]
target = checkpoint["target"]
print("Model loaded successfully!")
もし、別のnotebookで読み込む場合は、SelfiesVAEWithRegressorを再度定義してください。
下記コードでベンゼンlikeな分子を生成させます。もし変換したい分子が別にある場合は、base_smilesの変数に自分が入力したい分子のSMILESを入れてみてください。
base_smiles = "c1ccccc1" # 入力したい分子
N_GEN_LOCAL = 20 # 生成したい分子数
noise_scale_local = 0.75 # どれくらいbaseから離すか
loaded_model.eval()
# 1) SMILES -> canonical SMILES -> SELFIES -> ID列
mol_bz = Chem.MolFromSmiles(base_smiles)
can_bz = Chem.MolToSmiles(mol_bz, canonical=True)
selfies_bz = sf.encoder(can_bz)
ids_bz = encode_selfies(selfies_bz, max_len=max_len)
x_bz = torch.tensor([ids_bz], dtype=torch.long, device=device) # [1, T]
# 2) 入力分子をエンコードして μ, σ を取得
with torch.no_grad():
mu_bz, logvar_bz = loaded_model.encode(x_bz) # [1, latent]
std_bz = (0.5 * logvar_bz).exp() # [1, latent]
# 3) 入力分子の μ の近傍に N_GEN_LOCAL 個サンプル
eps = torch.randn(N_GEN_LOCAL, mu_bz.size(-1), device=device)
z_base = mu_bz.expand(N_GEN_LOCAL, -1) # [N, latent]
z_local = z_base + noise_scale_local * std_bz.expand_as(z_base) * eps
# 4) 潜在ベクトル → SELFIES ID列へデコード
gen_ids_local = loaded_model.sample(
z_local, p=0.75, temperature=0.6, use_topp=True
)
# 5) SELFIES -> SMILES -> Mol フィルタ
mols_local, smiles_local, selfies_local = [], [], []
for i in range(gen_ids_local.size(0)):
gen_sfs = ids_to_selfies(gen_ids_local[i].tolist())
normalized_sfs = normalize_generated_selfies(gen_sfs)
if normalized_sfs is None:
continue
try:
gen_smi = sf.decoder(normalized_sfs)
except Exception:
continue
m = Chem.MolFromSmiles(gen_smi)
if m is None:
continue
# # 必要なら drug-like フィルタ
# if not ok_druglike_molecule(m):
# continue
mols_local.append(m)
smiles_local.append(gen_smi)
selfies_local.append(normalized_sfs)
print(f"Base-molecule-centered generation: {len(mols_local)}/{N_GEN_LOCAL} molecules passed filters")
# 生成できた分子に対してターゲット予測
if mols_local:
target_preds_local = predict_target_from_selfies_list(
loaded_model, selfies_local, max_len=max_len, tta_n=0
)
# ラベル名など
label_map = {
"logP": ("logP", "{v:.2f}"),
"qed": ("QED", "{v:.3f}"),
"SAS": ("SAS", "{v:.2f}"),
"sas": ("SAS", "{v:.2f}"),
}
y_name, fmt = label_map.get(target, (target, "{v:.3f}"))
legends = [
f"{y_name}: " + fmt.format(v=v) for v in target_preds_local
]
img = Draw.MolsToGridImage(
mols_local, molsPerRow=5, subImgSize=(200, 200),
legends=legends
)
display(img)
plt.figure(figsize=(6, 4))
plt.hist(target_preds_local, bins=10, alpha=0.7, edgecolor="black")
plt.xlabel(y_name)
plt.ylabel("Count")
plt.title(f"Benzene-centered generation — {y_name} distribution")
mu = float(np.mean(target_preds_local))
plt.axvline(mu, linestyle="--", label=f"Mean: {fmt.format(v=mu)}")
plt.legend()
plt.show()
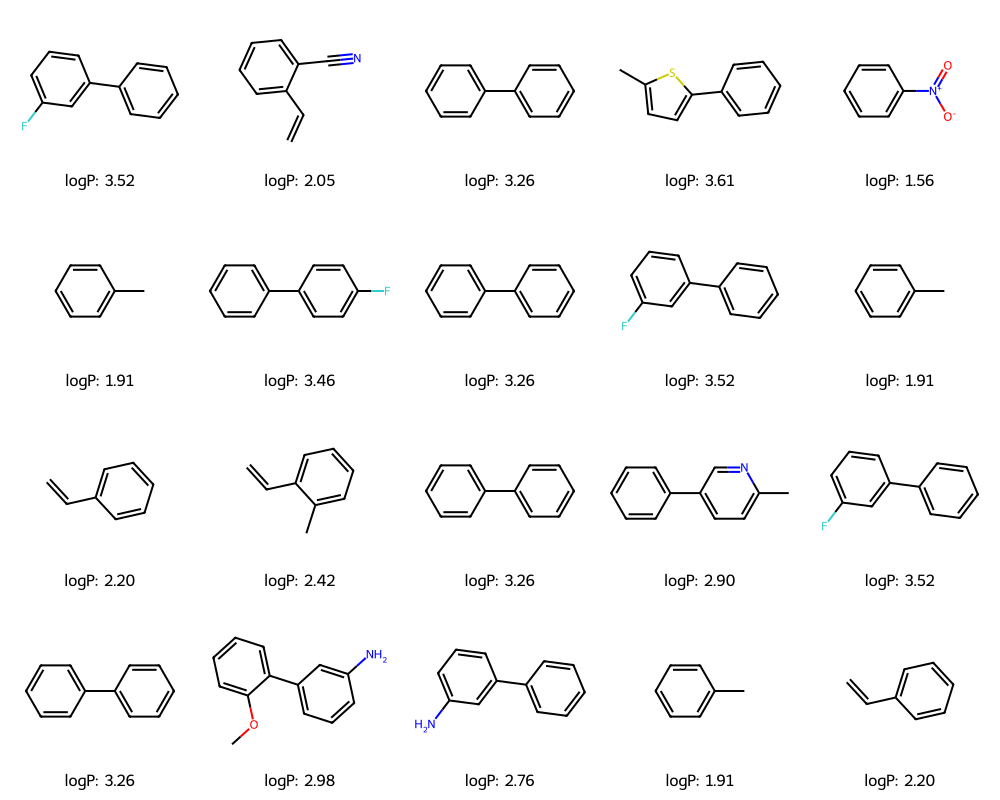
ニトロベンゼンやトルエンが生成され、類似分子の生成に成功しました。
noise_scale_localの値に結構敏感なので、いろいろいじってみると面白いです。重複している分子もいますが、予測されたlogPの値も同一の値となっており、回帰ヘッドも問題なく機能しています。
ベイズ最適化(BO)
最後に、論文通りベイズ最適化を使って欲しい物性値が改善するように分子を生成させてみます。今回はVAEに予測ヘッドを組み合わせているので、潜在空間で最適化を行い、objectiveが大きい分子を探索できる可能性があります。目的関数は、「5 × QED − SAS」としており、これを最大化するように潜在空間を最適化していきます。
まずは最初に読み込んだdatasetにて目的関数を計算し、percentileを計算する関数を定義しておきます。
dataset["qed_val"] = dataset["qed"].astype(float)
dataset["sas_val"] = dataset["SAS"].astype(float)
# 論文と同じ目的関数: 5 * QED - SAS
dataset["obj_5qed_minus_sas"] = 5.0 * dataset["qed_val"] - dataset["sas_val"]
# ZINC の目的関数分布からパーセンタイルを計算
# 目的関数 f = 5*QED - SAS が、ZINC 全体の中でどの位置にあるか
# (0〜100 % タイル)をログや可視化に使うためのユーティリティ
obj_all = dataset["obj_5qed_minus_sas"].astype(float).to_numpy()
obj_sorted = np.sort(obj_all)
def objective_percentile(value: float) -> float:
"""
目的関数値 value (= 5*QED - SAS) が、
ZINC データセット全体の中で何パーセンタイルに相当するか (0〜100) を返す。
"""
return 100.0 * (obj_sorted <= value).sum() / len(obj_sorted)
こちらの関数は後程使います。このpercentileが良くなるようにベイズ最適化を行うわけです。
次に、潜在ベクトルzと目的関数のペアを用意します。これらを Gaussian Process回帰モデルの学習データとして使うことで、「潜在空間上の任意の点 z に対して、f(z) の値を予測できる関数近似器」を作成します。
さっそく実装です。今回はsklearn baseのBOで行いますが、Pytorchを使ってるなら、BoTorchというNN専用のライブラリもあるそうです。これに関しては、次回の機会に。
# GP に使うサンプル数(論文に合わせて 2000)
N_GP = 2000
# ZINC 全体からランダムに N_GP 件だけ取り出す
df_gp = dataset.sample(n=min(N_GP, len(dataset)), random_state=1234).reset_index(drop=True)
print("GP train subset shape:", df_gp.shape)
Z_list = [] # 潜在ベクトル z を貯めるリスト
y_list = [] # 目的関数 y = 5*QED - SAS を貯めるリスト
model_with_reg.eval()
batch_size = 256
n_rows = len(df_gp)
with torch.no_grad(): # エンコードだけなので勾配は不要
for i in tqdm(range(0, n_rows, batch_size)):
chunk = df_gp.iloc[i:i+batch_size]
# SELFIES -> トークン ID 列
ids_batch = [encode_selfies(s, max_len=max_len) for s in chunk["SELFIES"].tolist()]
x = torch.tensor(ids_batch, dtype=torch.long, device=device) # [B, T]
# VAE エンコーダで潜在分布の平均 μ(と logvar)を取得
mu, logvar = model_with_reg.encode(x) # mu: [B, latent_dim]
# 目的関数 5*QED - SAS を numpy 配列として取り出す
y_chunk = chunk["obj_5qed_minus_sas"].astype(float).values # [B]
# CPU 上の numpy 配列にしてリストに追加
Z_list.append(mu.detach().cpu().numpy())
y_list.append(y_chunk)
# バッチごとに分かれていた配列を縦方向に連結
Z_gp = np.concatenate(Z_list, axis=0) # [N_GP, latent_dim]
y_gp = np.concatenate(y_list, axis=0) # [N_GP]
print("Z_gp shape:", Z_gp.shape)
print("y_gp shape:", y_gp.shape)
print("y_gp stats:")
print(" mean =", y_gp.mean())
print(" std =", y_gp.std())
print(" min =", y_gp.min())
print(" max =", y_gp.max())
GP train subset shape: (2000, 10)
Z_gp shape: (2000, 64)
y_gp shape: (2000,)
y_gp stats:
mean = 0.5748790819659909
std = 1.0361343386430921
min = -4.365874420664487
max = 2.9945121238408756
サンプルを2000個取り出し、それらの目的関数を計算しています。これにて、(z, y)のペアが揃いました。また、目的関数の統計値も計算し出力しています。
次にGaussian Process回帰モデルを定義し、学習させます。
# カーネルの定義
# RBF(ガウシアンカーネル) + WhiteKernel(ノイズ)
kernel = RBF(
length_scale=1.0,
length_scale_bounds=(1e-2, 1e2)
) + WhiteKernel(
noise_level=1e-3,
noise_level_bounds=(1e-5, 1e1)
)
gp = GaussianProcessRegressor(
kernel=kernel,
alpha=1e-10, # ノイズは WhiteKernel に任せる
normalize_y=True, # y(5*QED-SAS)を内部で標準化
n_restarts_optimizer=5,
random_state=1234,
)
# GP の学習
gp.fit(Z_gp, y_gp)
print("Optimized kernel:", gp.kernel_)
# トレーニングデータ上でのR²をざっとチェック
y_gp_pred = gp.predict(Z_gp)
gp_r2 = r2_score(y_gp, y_gp_pred)
print(f"GP train R²: {gp_r2:.3f}")
Optimized kernel: RBF(length_scale=3.94) + WhiteKernel(noise_level=0.000998)
GP train R²: 1.000
使用するカーネルは
RBF(Gaussianカーネル) + WhiteKernel(ホワイトノイズ)の和になります。
引数の説明として
-
length_scale(ℓ): RBF カーネルの「どのくらい滑らかに変化するか」を決めるパラメータ(大きいほど“ゆっくり変動する関数”になる) -
length_scale_bounds: 最適化時に探索する範囲 -
noise_level(σ_n²) : 観測ノイズの強さ。初期値 1e-3 に設定している -
noise_level_bounds: ノイズの範囲を指定
そして定義したカーネルを使いGaussian Process回帰モデルを定義しています。こちらの引数の説明として
-
normalize_y=True: ターゲットy_gpを内部で(y - mean) / stdのように正規化してから GP を学習させる -
n_restarts_optimizer=5: カーネルパラメータの最適化(対数マージナル尤度の最大化)を、異なる初期値から 5 回リスタートしてローカルミニマムを回避しやすくする
となっております。出力としては、R^2 = 1となり、完全一致となっています。Gaussian Process回帰モデルをベイズ最適化として使う観点では、トレーニングR^2が高いのはむしろ望ましいとのこと(チャッピーより)。
それでは、GPモデルが構築できたので、GPに入力する初期の分子をセレクトします。こちらも論文に従い、
- 目的関数(
5 × QED − SAS)の低い、下位10%に入る「特性の悪い分子群を抽出」 - その中から 1 分子をランダムに選び、最適化のスタート分子とする
- Start 分子を SELFIES → ID に変換して VAE エンコーダに通し、対応する潜在ベクトル
z0 = μを取得する
といった手順で行きます。
# 悪い」スタート分子を選ぶ
# 目的関数 f = 5*QED - SAS の分布から、
# 下位 10% に入る分子だけを「悪い分子」として抽出します。
# 5×QED−SAS の 10パーセンタイル(下位10%)を閾値にする
obj_q10 = dataset["obj_5qed_minus_sas"].quantile(0.10)
print("10th percentile of objective (5*QED - SAS):", obj_q10)
# 下位10%に入る分子だけ抽出(=性能の低い分子サブセット)
df_low = dataset[dataset["obj_5qed_minus_sas"] <= obj_q10].reset_index(drop=True)
print("Low-scoring subset shape:", df_low.shape)
# その中から 1 分子だけスタート分子としてランダムに選ぶ
# (再現性のため random_state を固定)
start_row = df_low.sample(n=1, random_state=42).iloc[0]
start_smiles = start_row["can_smiles"]
start_selfies = start_row["SELFIES"]
start_obj = float(start_row["obj_5qed_minus_sas"])
start_qed = float(start_row["qed_val"])
start_sas = float(start_row["sas_val"])
print("=== Start molecule (low objective) ===")
print("SMILES:", start_smiles)
print(f"QED: {start_qed:.3f} | SAS: {start_sas:.3f} | 5*QED - SAS: {start_obj:.3f}")
# 元データ側の分子構造をそのまま表示(VAE で再構成はしない)
mol_start = start_row["mol"]
display(Draw.MolToImage(mol_start, size=(250, 200)))
# スタート分子に対応する潜在ベクトル z0 を取得
# SELFIES -> トークン ID 列に変換し、VAE エンコーダに通す。
# 潜在分布 N(μ, σ^2) の平均 μ を「この分子に対応する潜在ベクトル z0」として使う。
ids_start = encode_selfies(start_selfies, max_len=max_len)
x_start = torch.tensor([ids_start], dtype=torch.long, device=device)
with torch.no_grad():
mu_start, logvar_start = model_with_reg.encode(x_start)
z0 = mu_start.squeeze(0).detach().cpu().numpy() # shape = [latent_dim]
print("z0 shape:", z0.shape)
10th percentile of objective (5*QED - SAS): -0.7665590347464312
Low-scoring subset shape: (24946, 10)
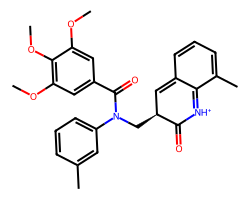
=== Start molecule (low objective) ===
SMILES: COc1cc(C(=O)N(C[C@H]2C=c3cccc(C)c3=[NH+]C2=O)c2cccc(C)c2)cc(OC)c1OC
QED: 0.566 | SAS: 3.699 | 5*QED - SAS: -0.867
z0 shape: (64,)
下位10%の分子群からランダムに1分子セレクトされました。目的関数の値も-0.867とよくない値になっています。これが良くなるようなzを探索していきましょう。
それでは、BOにおいて重要な獲得関数(Acquisition Function)を定義します。獲得関数にもいろいろ種類がありますが、今回はその中の期待改善量(Expected Improvement, EI)を使います。ざっくり説明すると、改善量の期待値で、EIが大きくなる時のzの候補が、目的関数が高くなるような可能性有というわけです。
# EIの実装
def expected_improvement(mu, sigma, f_best, xi=0.0):
"""
EI(x) = E[ max(0, f(x) - f_best - xi) ]
maximize したい目的関数 f に対する EI を計算する。
mu, sigma: GP の予測平均・標準偏差
f_best: これまでの最大観測値(または最大予測値)
xi: 0〜0.1 程度の探索パラメータ(大きいほど探索寄り)
"""
mu = np.asarray(mu, dtype=np.float64)
sigma = np.asarray(sigma, dtype=np.float64)
sigma = np.maximum(sigma, 1e-9) # 0 除算回避
imp = mu - f_best - xi
Z = imp / sigma
ei = imp * norm.cdf(Z) + sigma * norm.pdf(Z)
ei[sigma <= 1e-9] = 0.0
return ei
def gp_bo_ei_with_path(
gp,
z0,
n_steps=30,
n_candidates=256,
step_size=0.5,
xi=0.0,
random_state=None,
verbose=True,
):
"""
Gaussian Process + EI (Expected Improvement) を使った
ベイズ最適化ループ(簡易実装)+軌跡の記録。
- 各ステップで、現在の best_z の周りに n_candidates 個サンプリング
- GP から (mu, sigma) を取得し、EI を最大化する点を次の候補に選ぶ
- best_z / best_score は「予測平均 mu が最大の点」で更新
(軌跡は単調増加になる)
戻り値
-------
z_path: [n_steps+1, latent_dim] (step 0 がスタートの z0)
score_path: [n_steps+1] (GP の予測平均 mu(best_z))
"""
rng = np.random.default_rng(random_state)
z0 = np.asarray(z0, dtype=np.float64)
dim = z0.shape[-1]
# 初期点の GP 予測値
mu0 = gp.predict(z0[None, :])[0]
best_z = z0.copy()
best_score = float(mu0)
if verbose:
print(f"[Step 00] mu(z0) = {best_score:.3f}")
z_path = [best_z.copy()]
score_path = [best_score]
for t in range(1, n_steps + 1):
# 1. 近傍に候補点をランダムサンプリング
cand = best_z[None, :] + step_size * rng.standard_normal((n_candidates, dim))
# 2. GP から (mu, sigma) を取得
mu, sigma = gp.predict(cand, return_std=True)
# 3. EI を計算し、最大 EI の点を次の候補に
ei = expected_improvement(mu, sigma, f_best=best_score, xi=xi)
idx_ei_best = np.argmax(ei)
z_next = cand[idx_ei_best]
# 4. その点の予測平均で best を更新(軌跡は best のみ記録)
mu_next = float(mu[idx_ei_best])
if mu_next > best_score:
best_score = mu_next
best_z = z_next
z_path.append(best_z.copy())
score_path.append(best_score)
if verbose:
pct = objective_percentile(best_score)
print(
f"[Step {t:02d}] mu_best = {best_score:.3f} "
f"(percentile ~ {pct:.2f}%)"
)
return np.stack(z_path, axis=0), np.array(score_path)
EIを獲得関数とするBOループを回すことで、潜在空間の中からf(z)の値が高くなりそうな点を順次提案します。
上記のgp_bo_ei_with_path関数は、このBO過程を実装したもので、各ステップでの「最も良いと予測される潜在ベクトル z」の軌跡z_pathと、そのときのGP予測値score_pathを返します。
この関数を使って、スタート点からの改善を図ってみます。
# 学習済み GP と、スタート点 z0 を使ってベイズ最適化を実行
z_path, score_path = gp_bo_ei_with_path(
gp,
z0,
n_steps=30,
n_candidates=1024,
step_size=0.2,
xi=0.01,
random_state=123,
verbose=True,
)
print("z_path shape :", z_path.shape) # (31, latent_dim)
print("score_path shape:", score_path.shape)
print("start mu:", score_path[0], "end mu:", score_path[-1])
start_pct = objective_percentile(score_path[0])
end_pct = objective_percentile(score_path[-1])
print(f"start percentile ≈ {start_pct:.2f}%")
print(f"end percentile ≈ {end_pct:.2f}%")
[Step 00] mu(z0) = -0.182
[Step 01] mu_best = 0.419 (percentile ~ 39.96%)
[Step 02] mu_best = 0.901 (percentile ~ 58.02%)
[Step 03] mu_best = 1.476 (percentile ~ 79.96%)
[Step 04] mu_best = 1.822 (percentile ~ 90.10%)
[Step 05] mu_best = 2.187 (percentile ~ 96.46%)
[Step 06] mu_best = 2.554 (percentile ~ 99.26%)
[Step 07] mu_best = 2.913 (percentile ~ 99.95%)
[Step 08] mu_best = 3.146 (percentile ~ 100.00%)
[Step 09] mu_best = 3.460 (percentile ~ 100.00%)
[Step 10] mu_best = 3.799 (percentile ~ 100.00%)
[Step 11] mu_best = 4.122 (percentile ~ 100.00%)
[Step 12] mu_best = 4.392 (percentile ~ 100.00%)
[Step 13] mu_best = 4.540 (percentile ~ 100.00%)
[Step 14] mu_best = 4.760 (percentile ~ 100.00%)
[Step 15] mu_best = 4.878 (percentile ~ 100.00%)
[Step 16] mu_best = 5.032 (percentile ~ 100.00%)
[Step 17] mu_best = 5.128 (percentile ~ 100.00%)
[Step 18] mu_best = 5.257 (percentile ~ 100.00%)
[Step 19] mu_best = 5.434 (percentile ~ 100.00%)
[Step 20] mu_best = 5.485 (percentile ~ 100.00%)
[Step 21] mu_best = 5.633 (percentile ~ 100.00%)
[Step 22] mu_best = 5.754 (percentile ~ 100.00%)
[Step 23] mu_best = 5.754 (percentile ~ 100.00%)
[Step 24] mu_best = 5.759 (percentile ~ 100.00%)
[Step 25] mu_best = 5.810 (percentile ~ 100.00%)
[Step 26] mu_best = 5.837 (percentile ~ 100.00%)
[Step 27] mu_best = 6.007 (percentile ~ 100.00%)
[Step 28] mu_best = 6.070 (percentile ~ 100.00%)
[Step 29] mu_best = 6.070 (percentile ~ 100.00%)
[Step 30] mu_best = 6.070 (percentile ~ 100.00%)
z_path shape : (31, 64)
score_path shape: (31,)
start mu: -0.18176015939819357 end mu: 6.069782006401782
start percentile ≈ 21.33%
end percentile ≈ 100.00%
step数が増えるにつれ、percentileが改善しています!!目的通り、良い物性に近づいているようです。
最後に可視化して終わりです。
# ベイズ最適化パス上の分子を可視化
# z_path で得られた潜在空間上の軌跡から、
# いくつかのステップをピックアップして SELFIES → SMILES → Mol に戻し、
# 分子構造と QED / SAS / 目的関数 / パーセンタイルを確認する。
# 可視化したい step(start〜end まで等間隔に抜いている例)
idx_list = [0, 5, 10, 15, 20, 25, 30]
z_sel = z_path[idx_list] # shape [len(idx_list), latent_dim]
# --- 潜在ベクトル z を VAE デコーダで分子に復元 ---
z_tensor = torch.tensor(z_sel, dtype=torch.float32, device=device)
with torch.no_grad():
# 潜在ベクトルから SELFIES のトークン列(ID列)をサンプリング
ids_batch = model_with_reg.sample(z_tensor, max_len=max_len)
mols = [] # Grid 描画用の RDKit Mol のリスト
metrics = [] # DataFrame 化用: (step, smiles, qed, sas, obj, pct)
for step_idx, ids in zip(idx_list, ids_batch.cpu().numpy()):
# ID 列 → SELFIES 文字列へ
selfies_i = ids_to_selfies(ids)
try:
# SELFIES → SMILES → Mol へ変換
smiles_i = sf.decoder(selfies_i)
mol_i = Chem.MolFromSmiles(smiles_i)
except Exception:
mol_i = None
if mol_i is None:
# デコードに失敗した場合はスキップ
continue
# RDKit / sascorer で QED / SAS / objective / percentile を再計算
qed_i = float(QED.qed(mol_i))
sas_i = float(sascorer.calculateScore(mol_i))
obj_i = 5.0 * qed_i - sas_i
pct_i = objective_percentile(obj_i)
mols.append(mol_i)
metrics.append((step_idx, smiles_i, qed_i, sas_i, obj_i, pct_i))
# --- 分子構造をグリッド表示(添え字なし、構造変化に集中して見る用) ---
img = MolsToGridImage(
mols,
molsPerRow=len(mols), # 1 行にすべて並べる(2x? にしたければ調整)
subImgSize=(250, 200)
)
display(img)
# --- 各 step の指標を DataFrame で表示(行 = step, 列 = 指標) ---
df_metrics = pd.DataFrame(
metrics,
columns=["step", "SMILES", "QED", "SAS", "obj_5qed_minus_sas", "percentile"]
)
# step 順にソートし、行インデックスとして使う
df_metrics = df_metrics.sort_values("step").set_index("step")
display(df_metrics)
| step | SMILES | QED | SAS | obj_5qed_minus_sas | percentile |
|---|---|---|---|---|---|
| 0 | COC=CC(C=O)N(C(C@H1)1C=C2C=C3C(C)=CC2=[NH1+1]... | 0.746344 | 5.839518 | -2.107799 | 1.400253 |
| 5 | C1OC=CC1(C=O)N(C(C@H1)1CC2=C–CC(#N)=C2CCC3... | 0.747968 | 4.861802 | -1.121962 | 6.004690 |
| 10 | COC–CC(C=O)N(C=O)N1CCCC1C(=C)C=O | 0.345921 | 3.014315 | -1.284710 | 4.725101 |
| 15 | CCOC=C1C(C=O)NCC(O)N2CCCC2–C)C1=O | 0.571718 | 2.780211 | 0.078379 | 28.631216 |
| 20 | COC1–CC=C(C=O)NCC2=NC=C(C2)C=C1 | 0.928832 | 1.822880 | 2.821282 | 99.898980 |
| 25 | CCOC=C1C= C(C=O)NCC2=CC=CC=C2)CC=C1 | 0.840894 | 2.877074 | 1.327395 | 74.631898 |
| 30 | CCOC=C1C–C(NC(=O)CNC2=CC–CC=C2)C=C1 | 0.789734 | 2.740121 | 1.208550 | 70.042693 |
ベイズ最適化で得られた潜在ベクトルの軌跡z_pathから、いくつかのステップ(ここでは 0, 5, 10, …, 30)を抜き出し、VAE デコーダを通して再び SELFIES/SMILES に変換しました。
左から右に行くにつれて、step数が進んでいきます。step20の分子が最も目的関数、percentileが高いようです。
step0の分子がさっきのスタート分子と違うやんと思います。これは、出力は間違ってなく、元のスタート分子はZINCのデータセットから抽出した生の分子、今回表示しているstep0の分子は、そのスタート分子をVAEに入力して、デコードされた分子となります。スタート分子由来であることには違いはないのですが、実装の都合上、同じ分子ではなくなります。ここは論文通りではないのです![]()
ただし、stepが更新されるにつれ目的関数が改善していく流れは再現することができました!!
所感
今回は物性予測も行うChemical VAEを実装しました。単に分子を生成して物性を予測するだけでなく、BOもかますことで所望の物性値を有す可能性がある分子を生成するという点が非常に有用だと感じています。
BO自体はいろんな場面で使用されていますが、説明変数Xの候補が出てきても、そこから具体的な分子を提案するのが難しいと思います。例えば、RdkitやMordredなどの分子記述子は値が出たとしても、そこから分子構造への逆変換はできません。一方、VAEは潜在ベクトルzと目的関数のペアとしてBOを実行することができ、得られるzは学習済みVAEでデコードすれば具体的な分子構造が得られるわけです。次のターゲットを考慮するときに見やすい、判断しやすいかと。
精度に関しては賛否両論ですが、実務的な観点として、ちゃんとしたデータを食わせれば精度向上し、有用な手段になりうると思います。
今度は別のデータセットでBoTorch baseで実装してみようと思います。長文読んでいただき有難うございました![]()
引用
・chemical_vae GitHub
オリジナルのコードです。Tenosorflowで実装されています。そのままcloneすれば使えるみたい。
・化学構造生成器 Chemical VAE の使い方
実際に上記GitHubからVAEを動かしているブログです。参考にさせていただきました。