化学×AI: 機械学習でPL波長を予測する（第3回：出力結果の妥当性判断）

そのモデルの出力本当に正しいですか？？

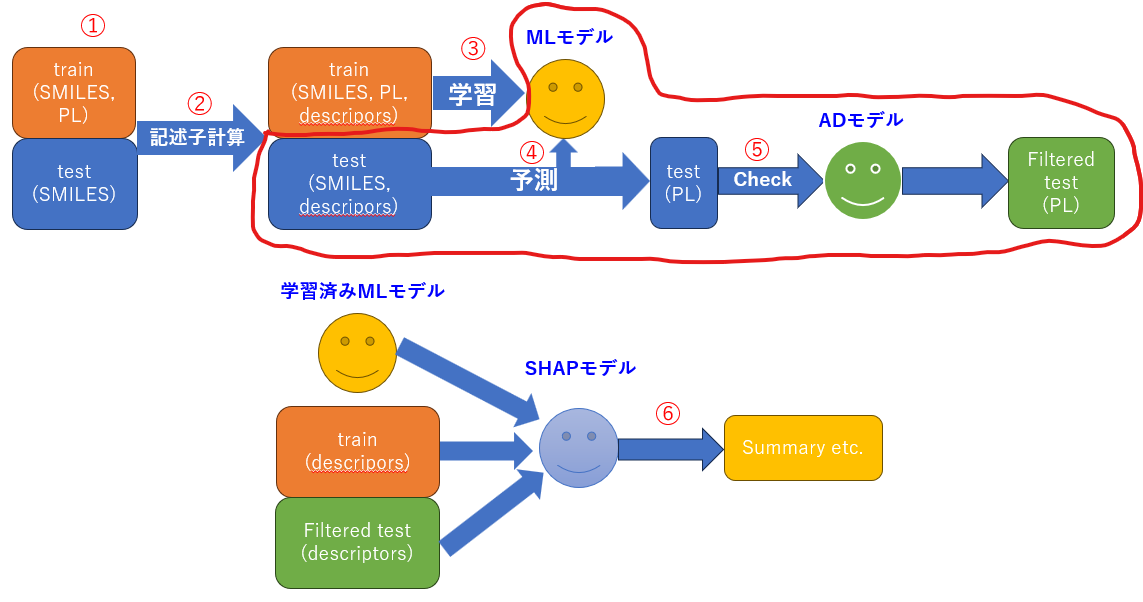
ということで第3回始めていきます。前々回で自分の持っている材料と未知のデータの分子記述子を計算し、説明変数を準備しました。前回はその計算されたデータセットに対して、様々なモデルを学習&予測させて汎化性能を評価しました。

• 第1回：記述子計算とデータ可視化(記述子の計算が終わっていない人はまずこちら！)
  https://qiita.com/Osarunokagoya/items/cc0f79e3a3d959de8635

• 第2回：予測モデルの構築(予測モデルが出来上がっていないひとはこちら！)
  https://qiita.com/Osarunokagoya/items/fbf618c29ba6c0f85253

今回はモデルの出力が信用できるかどうかをなるべく定量的に評価していこうと思います。手元に正解データのない材料を予測してみて、Application Domain(適用範囲)を考慮して信用できるか判断します。

いろんなMLの論文や学会報告を見てきましたが、精度の良いモデルを作ったという報告は多々ある一方で、モデルの出力が本当に信用できるかどうかをきちんと説明できている報告はまだ少ないように感じます。今回は金子先生の書籍で使用されていたAD modelを使って、未知のデータが学習データの範囲に収まっているかどうかを確認してみます。

それでは、行きましょう！！第三回スタートでございます！！

1. データの読み込み

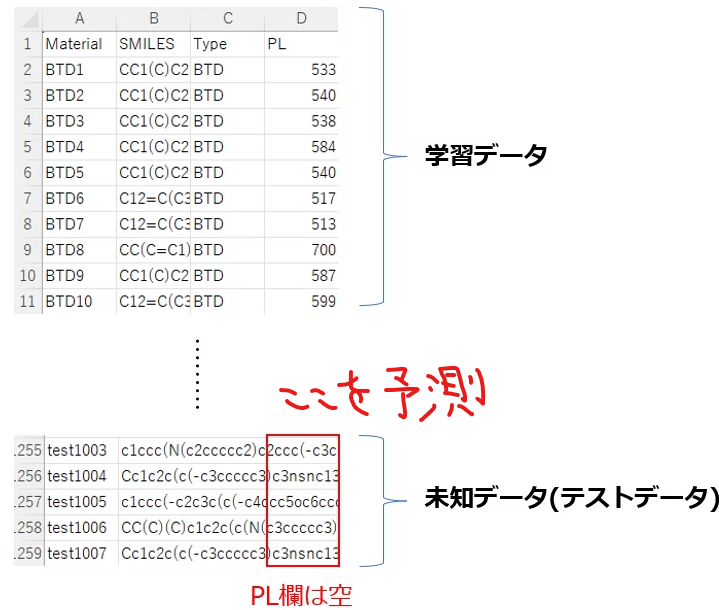
まずは前回同様データを読み込みます。今回予測の対象となるのは正解データを持っていない未知のデータです。

# 入力：読み込みたい記述子のタイプを選択
descriptor_type = 'mordred_3d'  # 'rdkit' or 'mordred_2d' or 'mordred_3d'

# ベースのデータ
dataset = pd.read_csv('material_data.csv', index_col=0)

# 条件に応じて記述子ファイルを読み込む
if descriptor_type == 'rdkit':
    des = pd.read_csv('descriptor_rdkit.csv', index_col=0)
elif descriptor_type == 'mordred_2d':
    des = pd.read_csv('descriptor_mordred_2d.csv', index_col=0)
elif descriptor_type == 'mordred_3d':
    des = pd.read_csv('descriptor_mordred_3d.csv', index_col=0)
else:
    raise ValueError(f"未知のdescriptor_type: {descriptor_type}")

# 結合
dataset_full = pd.concat([dataset.reset_index(), des.reset_index(drop=True)], axis=1)
dataset_full = dataset_full.set_index('Material')

# 確認
print(dataset.shape, des.shape, dataset_full.shape)

(1258, 3) (1258, 1480) (1258, 1483)

今回もMordredの3次元分子記述子にしました。ちなみに欠損値処理すると、2次元も3次元も同じ配列数となったので、正直RDKitかMordredを選ぶだけになっています。前回の結果から全体的にMordredの方が予測精度が安定していたので、こちらを採用します。

前回モデルが学習した記述子を選んでください。学習していない記述子を選んでしまうと、モデルの予測の際に配列数が違うというエラーが出ます。例えば、第2回の時にMordred_2dを選んだなら、今回もMoredred_2dを呼び出すということです。

次にデータセットを学習データとテストデータに分けます。

# TypeとSMILESを消す
dataset_full = dataset_full.drop(['SMILES', 'Type'], axis=1)

# 学習用と予測用に分ける
dataset_train = dataset_full.dropna(subset=['PL']).copy()
dataset_test = dataset_full[dataset_full['PL'].isnull()].copy()

# 予測データのPLは空なので消す
dataset_test = dataset_test.drop('PL', axis=1)

# 1. 両方のデータセットでinfをNaNに置き換える
dataset_train.replace([np.inf, -np.inf], np.nan, inplace=True)
dataset_test.replace([np.inf, -np.inf], np.nan, inplace=True)

# 2. 学習データに基づいて削除すべき列を特定する
#    - NaNを含む列
nan_cols = dataset_train.columns[dataset_train.isnull().any()]
#    - 標準偏差が0の列
zero_std_cols = dataset_train.columns[dataset_train.std() == 0]

#    - 削除する列の全リスト (重複をなくす)
cols_to_drop = nan_cols.union(zero_std_cols)
print(f"学習データに基づいて削除する列の数: {len(cols_to_drop)}")

# 3. 特定した同じ列を「両方のデータセット」から削除する
dataset_train.drop(columns=cols_to_drop, inplace=True)
dataset_test.drop(columns=cols_to_drop, inplace=True, errors='ignore') # テストデータにその列がなくてもエラーにしない

# 4. テストデータに残っているNaNを「学習データの平均値」で埋める
#    まず、学習データから各列の平均値を計算します。
imputation_values = dataset_train.drop('PL', axis=1).mean()

#    計算した平均値を使ってテストデータの欠損値を埋めます。
dataset_test.fillna(imputation_values, inplace=True)

print("\n処理後のshape:")
print(dataset_train.shape, dataset_test.shape)

学習データに基づいて削除する列の数: 208

処理後のshape:
(251, 1220) (1007, 1219)

テストデータはPL列がないので、処理後の列数は(学習データの列数 - 1)となります。何をしているかというと、テストデータのPL列は空欄なので、それを利用して学習データとテストデータに分けています、dropnaの引数でsubset='PL'としているところです。これによりPLが空欄となっているテストデータが除かれ、学習データのみとなります。次にPL欄が空欄のindexを取り出すことで、テストデータのみを取り出しています。そしてテストデータにおける欠損値は学習データの平均を使って埋めます。

この辺はデータセットをどう準備するかでコードの内容が変わってきますが、注意点としては以下の二つが挙げられます。

• 学習データとテストデータは一緒に記述子計算したほうが楽(第1回参照)、別々に計算してしまうと、計算された記述子の数が合わないことがあり列数がずれてしまい、追加で処理が必要となるため面倒。。。

• 前処理も学習データを基準に行う。例えば、標準偏差が0の列を探すときは学習データで探して、対象の列を学習データとテストデータ両方で消す。これも別々にやってしまうと、列数がずれてしまい後々計算できなくなる。。。

です。以前は学習データとテストデータを別々のエクセルにして読み込んで計算していたのですが、記述子計算後や後処理後に列数を確認してみると、列数が違うことが多々あり苦戦しました。

本題に戻りましょう。後処理された学習データとテストデータの変数名を混乱を避けるため、変更しておきます。X_testが未知の材料における説明変数で、これを学習済みモデルに入力します。

# 最終的な特徴量
X_train_all = dataset_train.drop(columns='PL')
y_train_all = dataset_train['PL']
X_test = dataset_test.copy()

2. モデルの読み込み&予測

第2回で作った学習済みのモデルを呼び出しましょう。

# モデルタイプを選択, 'rf', 'lgb', 'xgb' のいずれか
model_type = 'lgb'

# モデルとスケーラーを読み込み
base_dir = os.path.join('models', model_type)
model_loaded = joblib.load(os.path.join(base_dir, f'model_{model_type}.pkl'))
X_scaler_loaded = joblib.load(os.path.join(base_dir, 'X_scaler.pkl'))
y_scaler_loaded = joblib.load(os.path.join(base_dir, 'y_scaler.pkl'))

print(f"{model_type} モデルを読み込みました")

lgb モデルを読み込みました

前回、実行しているノートブックやpyファイルと同じ階層にmodelsというフォルダを作り、そこに各モデルやスケーラーを保存していると思います。もし保存がうまくいっている場合は、このコードで最初のmodel_typeを変更すれば、好きなモデルを呼び出すことができます。まずは決定木系のアンサンブルモデル3つのいずれかを呼び出すようにしていますが、NNは呼び出し方法が異なるので後で説明します。まず、ここではLightGBMを呼び出しました。

それでは、さっそく未知のデータを予測してみましょう!!

# 標準化する
autoscaled_X_train = X_scaler_loaded.transform(X_train_all)
autoscaled_X_test = X_scaler_loaded.transform(X_test)

# 予測&変換
y_test_pred_scaled = model_loaded.predict(autoscaled_X_test)
y_test_pred = y_scaler_loaded.inverse_transform(y_test_pred_scaled.reshape(-1, 1))
y_test_pred = pd.DataFrame(y_test_pred, columns=['pred_PL'], index=dataset_test.index)

print("予測結果:")
print(y_test_pred)

予測結果:
             pred_PL
Material            
test1     548.133021
test2     661.383186
test3     595.575955
test4     625.914937
test5     573.169063
...              ...
test1003  485.766622
test1004  511.684555
test1005  591.184512
test1006  566.132198
test1007  532.122297

未知のものに対して新しく数字を出すときはいつも緊張しますね。。。一方で、世の中で初めて数字をつけれたという成功体験は嬉しいものです（まだ成功しているかはわからんが。。。）

脱線したので解説に戻りますと、スケーラーは既に学習済み(fit_transform済み)なので、テストデータはtransformするだけでOKです。呼び出したモデルに予測させて、標準化を元に戻して、pd.DataFrame形式にして出力しています。

それでは、ここからが本記事のメイン？であり、この予測結果が本当に正しいのか考えてみましょう。まずはApplication Domain(適用範囲)をAD modelを使って構築してみます。適用範囲とは、予測モデルが信頼できる入力領域のことで、テストデータが学習データに似ているかを判断し、予測値の信頼性を評価できます。学習データは実測値で信頼できるものなので、「信頼できる学習データに似ているテストデータは信頼できる」という考え方です。

種々のAD modelがあるので、ここでは3つ紹介します。

3. AD model

■ OCSVM (One Class Support Vector Machine)

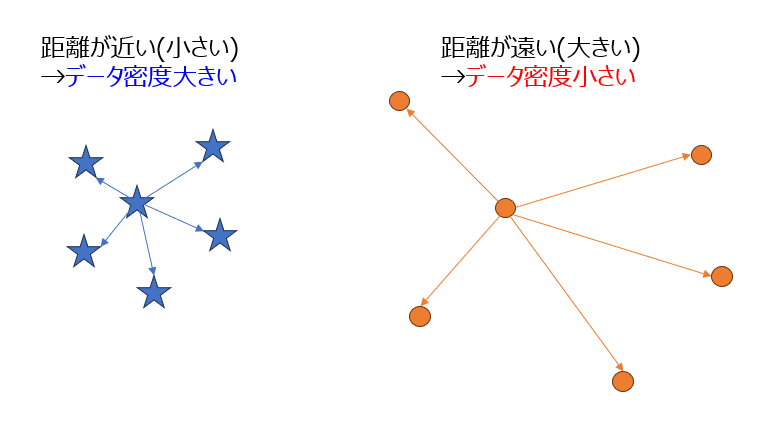
「1種類のクラス（学習データ）だけで境界を学習し、未知の外れ値を判定する手法」です。異常検知などに使われます。ざっくり原理を説明すると、学習データを多次元空間に写像し、その空間の中で境界を作ります。この時、全ての学習データが原点から離れた位置にプロットされるように境界を引きます(マージン最大化)。この境界の中をAD内、外側をAD外とするわけです。そして元の空間に戻した時に、先の多次元空間にて境界の内側にあって境界から離れているサンプルほど、データ密度は正で値が大きくなり、高次元空間にて境界の外側にあり境界から離れているサンプルほど、データ密度は負で値が大きくなります。

↓詳細は金子先生が説明してくれています。

サポートベクターマシンのハイパーパラメータを最適化する必要があるのですが、こちらも金子先生の手法を用いて決めます。gammaとnuがあり、gammaはカーネル関数におけるグラム行列の分散を最大化することにより求まります。↓詳細はこちら。

コード行きましょう、金子先生の書籍から引用です。グラム行列が最大となるときのgammaを返す関数です。

def gamma_optimization_with_variance(x, gammas):
    
    print('カーネル関数においてグラム行列の分散を最大化することによりγの最適化')

    # γの分散を格納
    variance_of_gamma_matrix = []

    # グラム行列の分散を計算
    for index, ocsvm_gamma in enumerate(gammas):
        # print(index + 1, '/', len(gammas))
        gram_matrix = np.exp(-ocsvm_gamma * cdist(x, x, metric='sqeuclidean'))
        variance_of_gamma_matrix.append(gram_matrix.var(ddof=1))

    # グラム行列が最大となるときのgammaを返す
    return gammas[variance_of_gamma_matrix.index(max(variance_of_gamma_matrix))]

定義した関数を使ってgammaを決めます。nuもこの際一緒に決めてしまいましょう。学習データの各説明変数が正規分布に従うと仮定して、一時的なnuの値を設定します。nuの値が大きくなると、ADは狭まるが誤差は小さくなり、nuの値が小さくなると、ADは広がるが誤差は大きくなります(正規分布における1σ, 2σ, 3σの関係)。ただ、最終的にpercentile（分位点）でもキャリブレーションし、AD範囲の調整を行うので、nuは小さめにして最初はADの範囲を広めにとっておきます。

# OCSVMによるAD
# OCSVMにおけるnu, nu=0.317(σ), nu=0.045(2σ), nu=0.003(3σ)など選択でき、学習時の境界の形・きつさを決めるハイパラ
# 学習データのうち、最大でnuだけを境界の外にしても良いという上限を与える（サポートベクタ比の下限）
# nuの値が大きくなるとADは狭まるが誤差は小さくなり、nuが小さくなるとADは広がるが、誤差は大きくなる
# nu=0.317ならば、約68%のデータが含まれる範囲（±1σ相当）を定義するイメージ、ただし直感的なイメージであって、厳密な対応ではない。
ocsvm_nu = 0.003

# γの候補
ocsvm_gammas = 2 ** np.arange(-20, 11, dtype=float)

# グラム行列の分散を最大化することによるγの候補、最も情報量の多いγを選ぶことができる
optimal_ocsvm_gamma = gamma_optimization_with_variance(autoscaled_X_train, ocsvm_gammas)

print('最適化されたgamma(OCSVM) :', optimal_ocsvm_gamma)

カーネル関数においてグラム行列の分散を最大化することによりγの最適化
最適化されたgamma(OCSVM) : 0.00048828125

これでgammaとnuの値が決まりました。今回は学習データの75%がAD内となるようにしたいので、percentileを使うことで75%のデータがAD内となるように調整します。OCSVMを呼び出し、各データのデータ密度を計算してみましょう。

# ADモデル構築
ocsvm_model = OneClassSVM(kernel='rbf', gamma=optimal_ocsvm_gamma, nu=ocsvm_nu)
ocsvm_model.fit(autoscaled_X_train)

# 学習データにおけるデータ密度を算出
data_density_train = ocsvm_model.decision_function(autoscaled_X_train)
# 下位25% をAD外にするように後付けでキャリブレーションする
threshold = np.percentile(data_density_train, 25)

# 予測データに対してADの内外を判定、学習データの分布（＝高密度領域）を学習する
# データ密度の値
data_density_test = ocsvm_model.decision_function(autoscaled_X_test)
in_ad_ocsvm = data_density_test >= threshold

# データ密度が閾値よりも大きい条件のみ抽出
y_test_pos_ocsvm = y_test_pred.iloc[in_ad_ocsvm, :].copy()

print(f"OCSVM-AD しきい値: {threshold:.6f}")
print(f"OCSVM-AD 内サンプル数: {in_ad_ocsvm.sum()} / {len(in_ad_ocsvm)}")

OCSVM-AD しきい値: 0.014955
OCSVM-AD 内サンプル数: 746 / 1007

テストデータ1007個のうち746個がAD内となりました。データ密度と予測した波長をプロットして可視化してみます。

# density ≥ threshold のインデックス
in_ad_index = data_density_test >= threshold
out_ad_index = data_density_test < threshold

# プロット
plt.figure(figsize=(6, 5))
plt.scatter(data_density_test[out_ad_index], y_test_pred.iloc[out_ad_index, 0], 
            color='gray', alpha=0.5, label='Outside AD')
plt.scatter(data_density_test[in_ad_index], y_test_pred.iloc[in_ad_index, 0], 
            color='blue', alpha=0.7, label='Inside AD')
plt.axvline(x=threshold, color='black', linestyle='--')  # しきい値の線
plt.xlabel('Decision Function Value (Density)')
plt.ylabel('Predicted y')
plt.legend()
plt.tight_layout()
plt.show()

先ほど決めたデータ密度の閾値よりも大きいものはAD内(青色)として認識され、小さいものはAD外(グレー)となっており外れ値として除外されていることが分かります。ひとまずこれでデータ密度が低い外れ値サンプルを除くことができました。

それでは、次のAD modelも見てみましょう。

誤解しやすいのが、学習データの75%をAD内にしたからといって、テストデータも75%がAD内となるわけではありません。これは学習データとテストデータにおける説明変数の分布が異なることに起因します。もちろんテストデータの分布が学習データの分布とぴったり重なれば75%となりますが、もちろんそんなことは無くズレます。学習データにも外れ値は含まれているので、その外れ値は除くようにADを構築し(今回の場合だと25%はカット)、構築したADをテストデータにも当てはめているということです。

■ k近傍法

分類モデルなどでよく使われるモデルです。説明変数の数が多い場合、各サンプルは多次元空間上の点として表現できます。その多次元空間における座標において、近接するk個の最近傍サンプルとの距離を求めて、平均距離を求めます。平均距離が小さい場合は近くにサンプルが多くデータ密度が高いということになり、逆に平均距離が大きい場合は近くにサンプルが少なくデータ密度が低いということです。AD modelとして使う場合は、学習データの平均距離の分布に閾値を設けることで、テストデータの平均距離がこの閾値よりも小さい(距離が近い)場合はAD内、大きい(距離が遠い)場合はAD外となるわけです。

では、コード行きましょう。

# kNNモデル作成
k = 5  # 近傍の数（調整可能）
knn_model = NearestNeighbors(metric='euclidean')
knn_model.fit(autoscaled_X_train)

# 学習データの自分を除いた平均近傍距離
dist_train, _ = knn_model.kneighbors(autoscaled_X_train, n_neighbors=k+1)
dist_train_no_self = dist_train[:, 1:]
mean_dist_train = dist_train_no_self.mean(axis=1)

# 距離が大きい25%をAD外とする
threshold = np.percentile(mean_dist_train, 75)

# テストデータの平均近傍距離(相手は学習集合なので、自己は存在しない)
dist_test, _ = knn_model.kneighbors(autoscaled_X_test, n_neighbors=k)
mean_dist_test = dist_test.mean(axis=1)

# 判定(TrueがAD内)
in_ad_knn = mean_dist_test <= threshold

# 予測結果のフィルタ
y_test_pos_knn = y_test_pred[in_ad_knn].copy()

print(f"kNN-AD しきい値: {threshold:.6f}")
print(f"kNN-AD 内サンプル数: {in_ad_knn.sum()} / {len(in_ad_knn)}")

kNN-AD しきい値: 25.134234
kNN-AD 内サンプル数: 779 / 1007

閾値は25となり、これよりも距離が小さい場合はAD内となっています。779個のサンプルがAD内となりました。可視化してみましょう。

# mean_dist_testがAD閾値より大きいか小さいかでインデックスを分ける
in_ad_index = mean_dist_test <= threshold
out_ad_index = mean_dist_test > threshold

# プロット
plt.figure(figsize=(6, 5))
plt.scatter(mean_dist_test[out_ad_index], y_test_pred.iloc[out_ad_index, 0], 
            color='gray', alpha=0.5, label='Outside AD')
plt.scatter(mean_dist_test[in_ad_index], y_test_pred.iloc[in_ad_index, 0], 
            color='blue', alpha=0.7, label='Inside AD')
plt.axvline(x=threshold, color='black', linestyle='--')  # しきい値（0）の線
plt.xlabel('mean_dist_test')
plt.ylabel('Predicted y')
plt.legend()
plt.tight_layout()
plt.show()

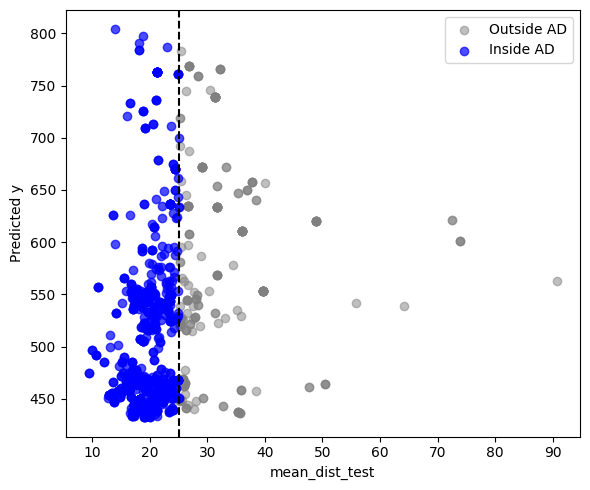
先ほどのOCSVMでは横軸がデータ密度でしたが、今回は平均距離なので、閾値よりも値の小さいサンプルがAD内となっていることが分かります。別のモデルでもADを設けて、外れ値サンプルを除くことができました。

最後にまた別のAD modelを構築してみましょう。

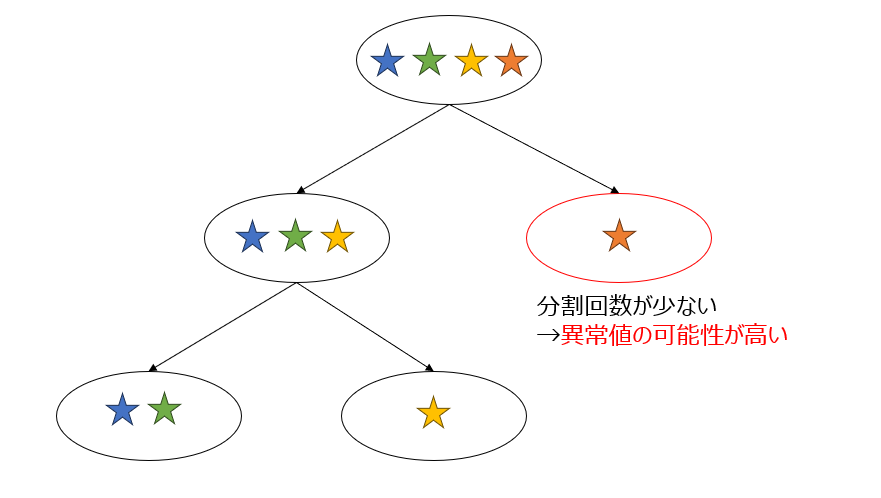
■ IsolationForest

決定木を使って外れ値サンプルを検出します。各データが孤立するまで分割を繰り返し、データが孤立するまでの分割回数（正式サイトではpath lengths）から異常値を検出するというのが基本的な考えです。データをランダムにサンプリングした上で、複数の決定木を用意し、作成した決定木の各データが孤立するまでの距離の平均を使用して異常値スコアを算出します。この辺はランダムフォレストっぽいですね。

実装してみます。

# IsolationForestの学習
iso_model = IsolationForest(contamination='auto', random_state=1234)
iso_model.fit(autoscaled_X_train)

# 学習スコア（大きいほど正常/AD内）
train_scores = iso_model.decision_function(autoscaled_X_train)

# 下位25% をAD外にするように後付けでキャリブレーションする
threshold = np.percentile(train_scores, 25)

# テストのAD判定
test_scores = iso_model.decision_function(autoscaled_X_test)
in_ad_iso = test_scores >= threshold

# 予測結果をフィルタ
y_test_pos_iso = y_test_pred[in_ad_iso].copy()

print(f"iso-AD しきい値: {threshold:.6f}")
print(f"iso-AD 内サンプル数: {in_ad_iso.sum()} / {len(in_ad_iso)}")

iso-AD しきい値: 0.060393
iso-AD 内サンプル数: 836 / 1007

contaminationという引数を調整することで、学習データに外れ値がどれくらい含まれているかの推定値を調整することができるそうです。つまり閾値の値をここで調整できます。ただ、前の2モデルと同様に、このモデルでもpercentileを使って閾値を調整するので、あまり気にせずdefaultの'auto'にしています。

このモデルではdecision_functionによりスコアが計算されます。このスコアが先ほど説明した平均パス長から計算した孤立のしやすさになります。短いパス長の場合、スコアが小さくなり異常サンプルとなるわけです。

今回も学習データにおいてスコアが高いサンプルの75%がAD内となるように閾値を決めています。IsolationForestの場合、836個のテストデータがAD内となりました。

最後に可視化します。

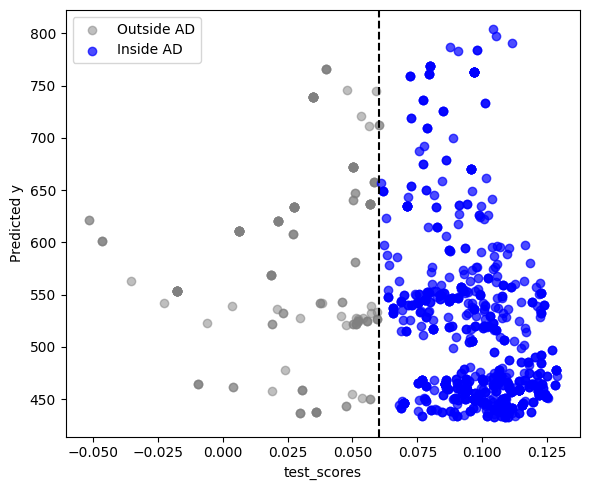
# test_scoresがAD閾値より大きいか小さいかでインデックスを分ける
in_ad_index = test_scores >= threshold
out_ad_index = test_scores < threshold

# プロット
plt.figure(figsize=(6, 5))
plt.scatter(test_scores[out_ad_index], y_test_pred.iloc[out_ad_index, 0], 
            color='gray', alpha=0.5, label='Outside AD')
plt.scatter(test_scores[in_ad_index], y_test_pred.iloc[in_ad_index, 0], 
            color='blue', alpha=0.7, label='Inside AD')
plt.axvline(x=threshold, color='black', linestyle='--')  # しきい値（0）の線
plt.xlabel('test_scores')
plt.ylabel('Predicted y')
plt.legend()
plt.tight_layout()
plt.show()

確かにIsolationForestだと、すこし多めのサンプルがAD内となっていることが分かります。

■ まとめ

Method	Threshold	Test in-AD count
OCSVM	0.014955	746
kNN (k=5)	25.134234	779
IsolationForest	0.060393	836

今まで見てきたように、どのモデルも学習データの75%がAD内となるようにADの枠を決めていますが、ADの構築方法、枠の範囲がモデルによって異なるため、テストデータを適用させたときの結果が変わっていることが分かります。そして、結局どのADモデルを使えばいいのかという疑問が残ります。一つの解決策としては、一番厳しい条件のADモデルを使う方法です。ここでいうとOCSVMですね。ADが狭いということは誤差も小さくなっているので信頼度は上がります。

ただ、それでもモデルによってADの構築する基準(サンプル間の距離、データ密度、パス長 etc.)が違うので、取りこぼしがある可能性もあります。よって、至った結論は全部使って最強のADを作ればいいやんという少し乱暴な考え方です('ω')笑

コード行きましょう。今まで各モデルで作ったADの共通部分を計算して、それを最終的なADとします。

# 各判定をAND条件で結合
in_all_ads = in_ad_ocsvm & in_ad_knn & in_ad_iso  # True: 全てでAD内

# 最終ADに通す
y_test_final = y_test_pred[in_all_ads].copy()

print(f"3モデルすべてでAD内と判定されたテストサンプル数: {len(y_test_final)}")

3モデルすべてでAD内と判定されたテストサンプル数: 701

3つのモデル全てにおいてAD内となるような学習データを基準にすることで、ADの枠をさらに狭めることができました。結果、AD内となるテストデータも減っていることが分かります。このようなアンサンブルADモデルによって定量的に信頼度が評価されたテストデータを入手することができました。

最後に人間の目でも、結果の確からしさを確認しておきましょう。テストデータのSMILESを読み込み、分子を可視化します。AD内の材料の場合、構造とPL波長が一緒に出力されます。AD外の材料は「AD外です」と出力され、PL波長は出力されません。numberという変数に見たい材料の「index番号-1」を入力してください。

# SMILESを含むCSVまたはExcelファイルを読み込む（例: test.csv）
df = pd.read_csv('material_data.csv', index_col=0)
df_test = df[df['PL'].isnull()].copy()

# 見たい番号（テスト集合中の位置）, 0~1006の数字を入力
number = 0

# インデックス名で特定
idx = df_test.index[number]
smiles = df_test.loc[idx, 'SMILES']
mol = Chem.MolFromSmiles(smiles)

# 可視化
img = Draw.MolToImage(mol, size=(300, 300), legend=str(idx))
img.show()

# 予測をインデックス名で参照（AD外なら KeyError を避ける）
if idx in y_test_final.index:
    print(y_test_final.loc[idx])
else:
    print(f'{idx} は AD外（y_test_final に存在しない）です')

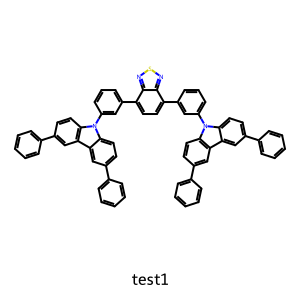
pred_PL    548.133021
Name: test1, dtype: float64

test1という材料の結果が出ました。548nmの発光波長はADにより保証されています。黄色らへんですね。BTDは緑からオレンジの発光を示す材料で、横にカルバゾールがついているので、若干CT性が向上し、redshiftしてそうなので妥当な結果です（専門用語つらつらすいません、この辺は気にしなくていいです）。

他の材料も見てみます。

pred_PL    523.091745
Name: test466, dtype: float64

ふむふむ、なるほど。

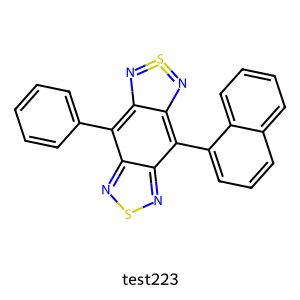
test223 は AD外（y_test_final に存在しない）です

あら、残念。

pred_PL    499.330887
Name: test778, dtype: float64

へー。

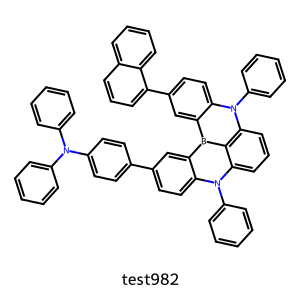
pred_PL    472.431153
Name: test982, dtype: float64

( ﾟДﾟ)

といった感じで、いろいろ遊んでみてください笑

最後に

第3回いかがでしたか。ADモデルで保証できる範囲を用意することにより、未知のデータに対する出力結果に信頼度を与えます。一方、精度の高いモデルを作れば、その時点で出力が保証されるという考えもあるかもしれませんが、外挿値を予測するのは難しく、間違った結果を与えてしまうことは大いにあり得ます。確度の高いデータを潤沢に持っている場合は、頑健な予測モデルが構築できるわけで、ADモデルが不要かもしれませんが。ただ個人でそんなにデータはたくさん持っているケースもレアだと思います。

もちろんADモデルで保証すれば絶対大丈夫というわけではなく、精度の高い予測モデルを構築できている前提で、そのモデルに学習させた学習データの分布から大きく外れていないテストデータであれば、ADモデルが保証できる可能性は高いということです。

それでは、いよいよ次回が最終回です(本当は今回をラストにしたかったが思いのほか長かった)。最後に学習データと保証された未知のデータの出力結果に対してSHAP解析を行い、モデルの解釈を議論していこうと思います。

長文、最後まで読んでいただきありがとうございました。

おまけ

NNで同様のことをしようと思うと、コードが若干異なるので記しておきます。モデルの呼び出し方法が異なります。以下のコードで実行してください。

# GPU set
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# パラメータなど読み込み
best_trial = joblib.load('models/nn/hparams.pkl')
feature_names = joblib.load('models/nn/feature_names.pkl')
# スケーラー読み込み
X_scaler = joblib.load('models/nn/X_scaler.pkl')
y_scaler = joblib.load('models/nn/y_scaler.pkl')

# define_modelを再定義（Optunaの設定と一致）
def define_model(trial, input_dim):
    layers = []
    n_layers = trial['n_layers']
    hidden_dim = trial['hidden_dim']
    dropout_rate = trial['dropout_rate']
    activation_name = trial['activation']
    use_batchnorm = trial['use_batchnorm']

    in_dim = input_dim
    for i in range(n_layers):
        layers.append(nn.Linear(in_dim, hidden_dim))

        if use_batchnorm:
            layers.append(nn.BatchNorm1d(hidden_dim))

        if activation_name == "relu":
            layers.append(nn.ReLU())
        else:
            layers.append(nn.LeakyReLU())

        layers.append(nn.Dropout(dropout_rate))
        in_dim = hidden_dim

    layers.append(nn.Linear(in_dim, 1))
    return nn.Sequential(*layers)

# 列順合わせ、標準化
X_test = X_test[feature_names]                
autoscaled_X_test = X_scaler.transform(X_test)

# テンソル変換
X_test_tensor = torch.tensor(autoscaled_X_test, dtype=torch.float32).to(device)

# モデル構築（trial情報を渡す）
model = define_model(best_trial, input_dim=len(feature_names)).to(device)

# 重み読み込み
state = torch.load('models/nn/final_model.pth', map_location=device)
model.load_state_dict(state)
model.eval()

Sequential(
  (0): Linear(in_features=1219, out_features=524, bias=True)
  (1): ReLU()
  (2): Dropout(p=0.011821131613319363, inplace=False)
  (3): Linear(in_features=524, out_features=524, bias=True)
  (4): ReLU()
  (5): Dropout(p=0.011821131613319363, inplace=False)
  (6): Linear(in_features=524, out_features=524, bias=True)
  (7): ReLU()
  (8): Dropout(p=0.011821131613319363, inplace=False)
  (9): Linear(in_features=524, out_features=1, bias=True)
)

第二回で保存してモデルの重みやハイパラなどを呼び出しています。ここが決定木モデルとの違いになります。あとは推論モードにして予測してしまえば、今まで同様出力が得られます。

# 推論
with torch.no_grad():
    y_test_pred_scaled = model(X_test_tensor).cpu().numpy()

# 逆スケーリング
y_test_pred = y_scaler.inverse_transform(y_test_pred_scaled)
y_test_pred = pd.DataFrame(y_test_pred, columns=['pred_PL'], index=dataset_test.index)

# 予測結果を表示
print(y_test_pred)

pred_PL
Material            
test1     558.755798
test2     697.464661
test3     644.675476
test4     619.315613
test5     565.570496
...              ...
test1003  482.010223
test1004  514.723389
test1005  604.059509
test1006  539.133606
test1007  556.219543

[1007 rows x 1 columns]

後はこの出力に対して、ADモデルをかませば今までと同じように信頼性を評価できます。

引用文献

・化学のためのPythonによるデータ解析・機械学習入門
https://datachemeng.com/post-4014/
今回も参考にさせていただきました。OCSVMに関して非常に丁寧に解説されています。

・k近傍法（kNN）でモデルの適用範囲（AD）を評価する！
https://qiita.com/oki_kosuke/items/2c0eba61ee24276d5d31
k近傍法によるADに関しては、こちらの記事を参考にさせていただきました。基本に忠実で分かりやすいです。

・異常検知手法 Isolation Forestの解説、スクラッチでの実装
https://qiita.com/tchih11/items/d76a106e742eb8d92fb4
IsolationForestに関しての説明が載っています。こちらも分かりやすかったので、参考にさせていただきました。