異常検知手法 Isolation Forestの解説、スクラッチでの実装

Isolation Forestとは

異常検知に用いられる手法の一つです。
名前からお察しの通り、Isolation ForestはRandom Forestと同様に決定木に基づいて構築されます。
決定木を各データが孤立するまで分割を繰り返し、データが孤立するまでの距離（深さ）から異常値を推定しよう、というのが基本的なアイディアです（Isolate＝孤立）。全データを使って決定木を一つだけ作成すると過学習してしまうので、データをサンプリングした上で、大量の決定木を作成し、作成した決定木の各データが孤立するまでの距離の平均を使用して異常値スコアを算出します。

なお、分割する際の閾値は変数の最大/最小値の範囲からランダムに選択されますが（普通の決定木は情報利得により閾値を決定）、この手順により異常値は早く孤立することが直感的に理解できる例があったのでそのまま記載します。

例えば、IQはだいたい100を中心に分布するよう調整されていますが、たまたまIQ3億のデータがあると、そのデータの区間は(80くらい, 3億)になります。この区間で分割する値をランダムに決める（一様分布とする）と、3億のデータ点がisolateされる確率はめちゃくちゃ高いですよね。

参考：https://www.mojirca.com/2019/12/isolation-forest.html

異常値スコアの算出方法

異常値スコアを算出する際は、孤立するまでの深さの平均をそのまま使用するのではなく、二分探索する際の平均の深さc(n)で正規化します。これによりスコアは0~1に収まる用になり、比較がしやすくなります。

スコアの解釈については下記の通りになります。

• スコアが1に近いと異常値である可能性が高い
• スコアが0.5よりはるかに小さい場合、通常値である可能性が高い
• 全てのデータのスコアが≒0.5のとき、サンプル全体に異常はない可能性が高い

実装

ここからはsklearnを使用した実装と、スクラッチでの実装を行ってきます。始めに使用するデータを生成します。

import pandas as pd
import numpy as np
import seaborn as sns

sns.set()
np.random.seed(123)

# 平均と分散
mean1 = np.array([2, 2])
mean2 = np.array([-2, -2])
cov = np.array([[1, 0], [0, 1]])

# 正常データの生成(2つの正規分布から生成)
norm1 = np.random.multivariate_normal(mean1, cov, size=100)
norm2 = np.random.multivariate_normal(mean2, cov, size=100)

# 異常データの生成(一様分布から生成)
lower, upper = -10, 10
anom = (upper - lower)*np.random.rand(10, 2) + lower

df = np.vstack([norm1, norm2, anom])
df = pd.DataFrame(df, columns=["feat1", "feat2"])

# 可視化
sns.scatterplot(x="feat1", y="feat2", data=df)

sklearnを使用した実装

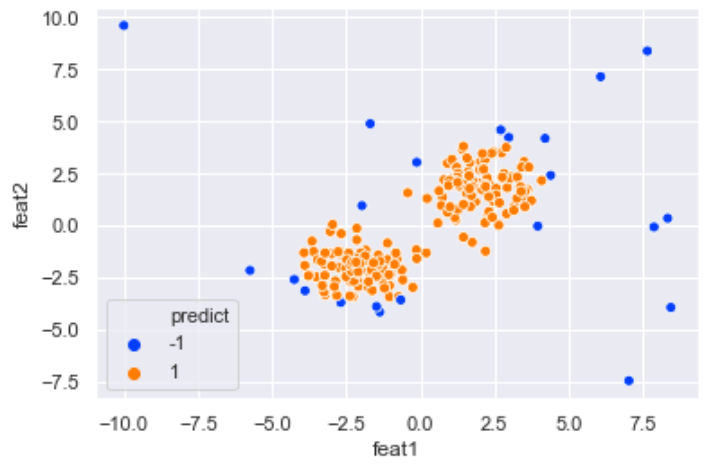
sklearnを使用すれば、数行で実装が可能です。-1が異常値（青）、1が通常値（オレンジ）となります。

# sklearnでの実装
from sklearn.ensemble import IsolationForest
sk_df = df.copy()

clf = IsolationForest(n_estimators=100, random_state=123)
clf.fit(sk_df)
sk_df["predict"] = clf.predict(sk_df)

# 可視化
sns.scatterplot(x="feat1", y="feat2", data=sk_df, hue='predict', palette='bright')

スクラッチでの実装

続いて、理解を深めるためにスクラッチでの実装を行います。
こちらのgitに公開されているコードを一部修正して、日本語のコメントを差し込んだ形となります。
https://github.com/tianqwang/isolation-forest-from-scratch/blob/master/iforest.py

まずは決定木を作るclassから。
ランダムに変数を決定→その変数の最大/最小値からランダムに閾値を決定→分割
の流れを分岐条件を保持しつつ、再起処理で繰り返します。今回の実装では、分割処理はデータが孤立する or 一定の深さまで到達するまで繰り返し行います。興味があるのは浅いところで孤立するデータなので、ある程度の深さまで到達すれば打ち切ってしまってOKという考え方です。

# 葉の情報と分岐条件を保存する箱
class LeafNode:
    def __init__(self, size, data):
        self.size = size
        self.data = data

# 分岐条件を保存する箱
class DecisionNode:
    def __init__(self, left, right, splitAtt, splitVal):
        self.left = left
        self.right = right
        self.splitAtt = splitAtt
        self.splitVal = splitVal

class IsolationTree:
    def __init__(self, height, height_limit):
        self.height = height
        self.height_limit = height_limit

    def fit(self, X: np.ndarray, improved=False):
        if isinstance(X, pd.DataFrame):
            X = X.values

        # 再起処理の終了要件（データが孤立する or 指定の深さに達する）
        if X.shape[0] <= 1 or self.height >= self.height_limit:  # gitではX.shape[0] <= 2だが、多分1が正しい
            # 葉の情報の保存
            self.root = LeafNode(size=X.shape[0], data=X)
            return self.root

        # 変数を1つランダムに抽出
        num_features = X.shape[1]
        splitAtt = np.random.randint(0, num_features)

        # 変数のmin/maxから閾値をランダムに決定し、2分割
        splitVal = np.random.uniform(min(X[:, splitAtt]), max(X[:, splitAtt]))
        X_left = X[X[:, splitAtt] < splitVal]
        X_right = X[X[:, splitAtt] >= splitVal]

        # 再起処理により分割を実施
        left = IsolationTree(self.height + 1, self.height_limit)
        right = IsolationTree(self.height + 1, self.height_limit)
        left.fit(X_left)
        right.fit(X_right)

        # 分岐条件の保存
        self.root = DecisionNode(left.root, right.root, splitAtt, splitVal)

        return self.root

続いてIsolationTreeを繰り返し作成し、path_length(孤立するまでの深さ）と異常値スコアを算出するクラスです。
各ツリーを作成する前に、指定した件数でデータのサンプリングを行います。

def c(size):
    # 二分探索する際の平均の深さc(n)の算出
    if size > 2:
        return 2 * (np.log(size-1)+0.5772156649) - 2*(size-1)/size
    if size == 2:
        return 1
    return 0


class IsolationTreeEnsemble:
    def __init__(self, sample_size, n_trees=10):
        self.sample_size = sample_size
        self.n_trees = n_trees

    def fit(self, X: np.ndarray, improved=False):
        if isinstance(X, pd.DataFrame):
            X = X.values

        # データの件数
        n_rows = X.shape[0]

        # 深さの上限の指定
        height_limit = np.ceil(np.log2(self.sample_size))

        # 指定の数だけIsolationTreeを作成
        self.trees = []

        for i in range(self.n_trees):

            # 指定した件数分、ランダムにデータを抽出
            data_index = np.random.randint(0, n_rows, self.sample_size)
            X_sub = X[data_index]

            # IsolationTreeを作成
            tree = IsolationTree(0, height_limit)
            tree.fit(X_sub)
            self.trees.append(tree)

        return self

    def path_length(self, X: np.ndarray) -> np.ndarray:
        paths = []

        # 各データを作成したツリーに当てはめ
        for row in X:
            path = []
            for tree in self.trees:
                node = tree.root

                # leafまで到達するまでの距離を測る
                length = 0
                while isinstance(node, DecisionNode):
                    if row[node.splitAtt] < node.splitVal:
                        node = node.left
                    else:
                        node = node.right
                    length += 1
                leaf_size = node.size

                # path lengthの算出。孤立する前に既定の深さに達した場合は+ c(leaf_size)で調整
                # ※ leaf_size=1のとき、c(leaf_size) = 0
                pathLength = length + c(leaf_size)

                path.append(pathLength)

            paths.append(path)

        # 深さの平均値を算出
        paths = np.array(paths)
        return np.mean(paths, axis=1)

    def anomaly_score(self, X: pd.DataFrame) -> np.ndarray:
        if isinstance(X, pd.DataFrame):
            X = X.values

        # 各データの深さの平均を算出し、その後異常値スコアを算出
        avg_length = self.path_length(X)
        scores = np.array([np.power(2, -l/c(self.sample_size)) for l in avg_length])
        return scores

##挙動確認
作成したクラスの挙動を確認します。sklearnに合わせて、スコアが閾値を上回る場合は-1（異常値）、下回る場合は1（通常値）でラベルをつけます。今回は閾値を0.5に設定しましたが、概ねsklearnと同じ結果が得られることが確認できます。

# 作成したクラスでの実装
scratch_df = df.copy()

# 閾値
thr = 0.5

scratch_tree = IsolationTreeEnsemble(sample_size=300)
scratch_tree.fit(scratch_df)
scratch_df["score"] = scratch_tree.anomaly_score(scratch_df)

# スコアが閾値を上回る場合は-1（異常値）、下回る場合は1（通常値）でラベル付け
scratch_df["predict"] = scratch_df.score.apply(lambda x: 1 if x < thr else -1)

# 可視化
sns.scatterplot(x="feat1", y="feat2", data=scratch_df, hue='predict', palette='bright')

参考

論文
https://cs.nju.edu.cn/zhouzh/zhouzh.files/publication/icdm08b.pdf

異常検出アルゴリズム Isolation Forest
ラベルなし異常検出アルゴリズムIsolationForestについて解説する
[異常検知入門と手法まとめ]
(https://qiita.com/kyohashi/items/c3343de3cfa236df3bda)
https://github.com/tianqwang/isolation-forest-from-scratch/blob/master/iforest.py

その他

別の異常検知の手法であるLocal Outlier Factor (LOF) についても理論解説、スクラッチでの実装を行っています。よろしければこちらの記事もご参照下さい。
Local Outlier Factor (LOF) の算出方法、スクラッチでの実装