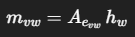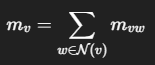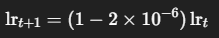OPVデータセットでGNNを動かしまくる：MPNN論文を追試して分かったこと

きっかけ

有機半導体のデータセットを探していたら、OPV(有機薄膜太陽電池)のデータセットにたどり着きました

National Renewable Energy Laboratory(NREL)が提供しているOPV材料のデータセットになります。分子構造を表すsmilesとHOMO, LUMO, gap(HOMOとLUMOの差)などの計算値が記載されています。

このデータセットを使ってGNNで物性を予測したのが、↓の論文で、今回はこの論文を追試しながらGNNの勉強をしたので、備忘録もかねてアウトプットしておきます。

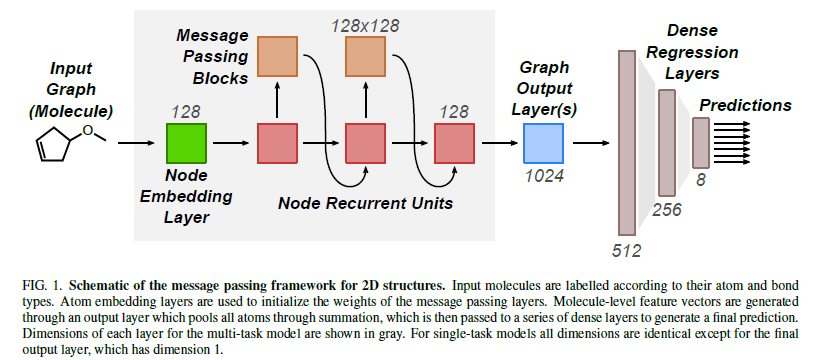
３次元構造を必要としないメッセージパッシングニューラルネットワーク(MPNN)についての論文です。MPNNはグラフニューラルネットワーク（GNN）の一種であり、「近傍ノードからメッセージを集約してノード状態を更新する」という GNN の基本構造を明示的に定式化した枠組みです。

論文のポイントは、3次元構造を使用せずとも2次元構造(smiles)のみで予測精度が出るところです。最適な3次元構造を用意するには、計算に時間のかかるDFT計算などが必要です。少量の材料数なら可能かもしれませんが、今回のデータセットのように数万となってくると現実的ではありません。そこで、2次元構造のみで物性値を予測できるGNNを構築できれば、ハイスループット用途として非常に有用となり得るというわけです。

それでは、実装行きます。

実装

ライブラリ読み込み

今回使ったライブラリとversionは以下の通りです。

import sys
import copy
import random
from collections import defaultdict

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import Dataset

from rdkit import Chem
from rdkit import __version__ as rdkit_version
from rdkit.Chem import Draw
from rdkit.Chem.Scaffolds import MurckoScaffold

from torch_geometric.data import Data
from torch_geometric.loader import DataLoader
from torch_geometric.nn import MessagePassing, global_add_pool
import torch_geometric

from tqdm.auto import tqdm

# ------------------------------
# Reproducibility
# ------------------------------
SEED = 1234
random.seed(SEED)
np.random.seed(SEED)
torch.manual_seed(SEED)
torch.cuda.manual_seed_all(SEED)

torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False

# ------------------------------
# Device
# ------------------------------
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# ------------------------------
# Environment info (for reproducibility)
# ------------------------------
print("===== Environment =====")
print(f"Python           : {sys.version.split()[0]}")
print(f"PyTorch          : {torch.__version__}")
print(f"PyTorch Geometric: {torch_geometric.__version__}")
print(f"RDKit            : {rdkit_version}")
if torch.cuda.is_available():
    print(f"CUDA version     : {torch.version.cuda}")
print("========================")
print("device:", device)

===== Environment =====
Python           : 3.9.23
PyTorch          : 2.2.1+cu121
PyTorch Geometric: 2.6.1
RDKit            : 2025.03.5
CUDA version     : 12.1
========================
device: cuda

GNNはtorch_geometricを使うと、簡単に実装できます。再現性確保のため、乱数seedも設定しました。

データセット読み込み & 前処理

使ったデータセットは以下の3つです。サイトには色々データセットがありましたが、論文で使っているデータセットは赤丸で示したものだと思われます。

圧縮された形でダウンロードし、解凍せずそのままpandasで読み込みました。そして、読み込んだ後にそれぞれのデータセットを全部くっつけました。

# ダウンロードしたデータセットを読み込む
dataset_train = pd.read_csv("data/NREL/smiles_train.csv.gz", index_col=0)
dataset_val = pd.read_csv("data/NREL/smiles_valid.csv.gz", index_col=0)
dataset_test = pd.read_csv("data/NREL/smiles_test.csv.gz", index_col=0)

# 全部くっつける
dataset_full = pd.concat([dataset_train, dataset_val, dataset_test], axis=0)

print("Train dataset size:", len(dataset_train))
print("Validation dataset size:", len(dataset_val))
print("Test dataset size:", len(dataset_test))
print("Full dataset size:", len(dataset_full))

Train dataset size: 80823
Validation dataset size: 5000
Test dataset size: 5000
Full dataset size: 90823

全部で9万個ほどあります。ダウンロードの段階で、学習・検証・テストに分かれていましたが、分割理由もわからないので、公平のため、後程ランダムにスプリットします。

このデータセットでは目的変数が8個あり、その中には、extrapolated（外挿値）と呼ばれる目的変数列が混ざっており、この外挿値のデータがないサンプルもありました。論文によりますと、溶液プロセス用の可溶性小分子はポリマーになることができないので、オリゴマーから外挿できる値がないとのことでした。

そこで、今回の実装では8個の目的変数すべてにデータが入っているサンプル（欠損値がないサンプル）のみ使用しました。以下のコードで整理します。

# 目的変数列（8個）
target_cols = ["gap", "homo", "lumo", "spectral_overlap", "homo_extrapolated", "lumo_extrapolated", "gap_extrapolated", "optical_lumo_extrapolated"]
required_cols = ["smile"] + target_cols

# 必須列の欠損チェック
missing_cols = [c for c in required_cols if c not in dataset_full.columns]
if missing_cols:
    raise ValueError(f"dataset_full に必要列がありません: {missing_cols}. columns={list(dataset_full.columns)}")

# 目的変数列が欠損している行を除外
df = dataset_full[required_cols].dropna().reset_index(drop=True)

# 型の安全化（smileはstr、ターゲットはnumeric）
df["smile"] = df["smile"].astype(str)
for col in target_cols:
    df[col] = pd.to_numeric(df[col], errors="coerce")
df = df.dropna(subset=target_cols).reset_index(drop=True)

print("Usable rows:", len(df))
print(df.head(3))

Usable rows: 54335
smile	gap	homo	lumo	spectral_overlap	homo_extrapolated	lumo_extrapolated	gap_extrapolated	optical_lumo_extrapolated
0	CC(C)(C)c1cc(Cc2ccc(-c3c4cc(-c5cc6c(-c7ccc(Cc8...	2.8229	-4.976962	-1.834319	1565.417406	-4.693964	-2.430793	1.9479	-2.746064
1	COP(=O)(OC)Oc1ccc(-c2c3cc(-c4cc5c(-c6ccc(Cc7cc...	2.8338	-5.083087	-1.922212	1427.499693	-4.770156	-2.532291	1.9418	-2.828356
2	Cc1sc(C)c2c3cc(-c4sc(-c5cc6c(-c7ccc(C(F)(F)C(F...	2.2093	-5.022949	-2.551067	4052.235421	-4.835191	-2.961959	1.5615	-3.273691

整理したところ、実装に使えるサンプルは5万個ほどでした。

ここで目的変数の中身を簡単に説明しておきます。

• gap : 時間依存DFTによって計算されたモノマーの第一励起エネルギー
• homo : モノマーの最高被占軌道エネルギー
• lumo : モノマーの最低空軌道エネルギー
• spectral_overlap : スペクトル重なり（ダイマーの光吸収スペクトルと AM1.5 太陽光スペクトルとの積分重なり）
• homo_extrapolated etc. : ポリマー極限に外挿された電子物性

とのことです。すべて計算値でGaussian 09にて実施されています。DFTの汎関数・基底関数はB3LYP/6-31g(d)とのこと。データセットに含まれるsmileはモノマー構造が記載されています。

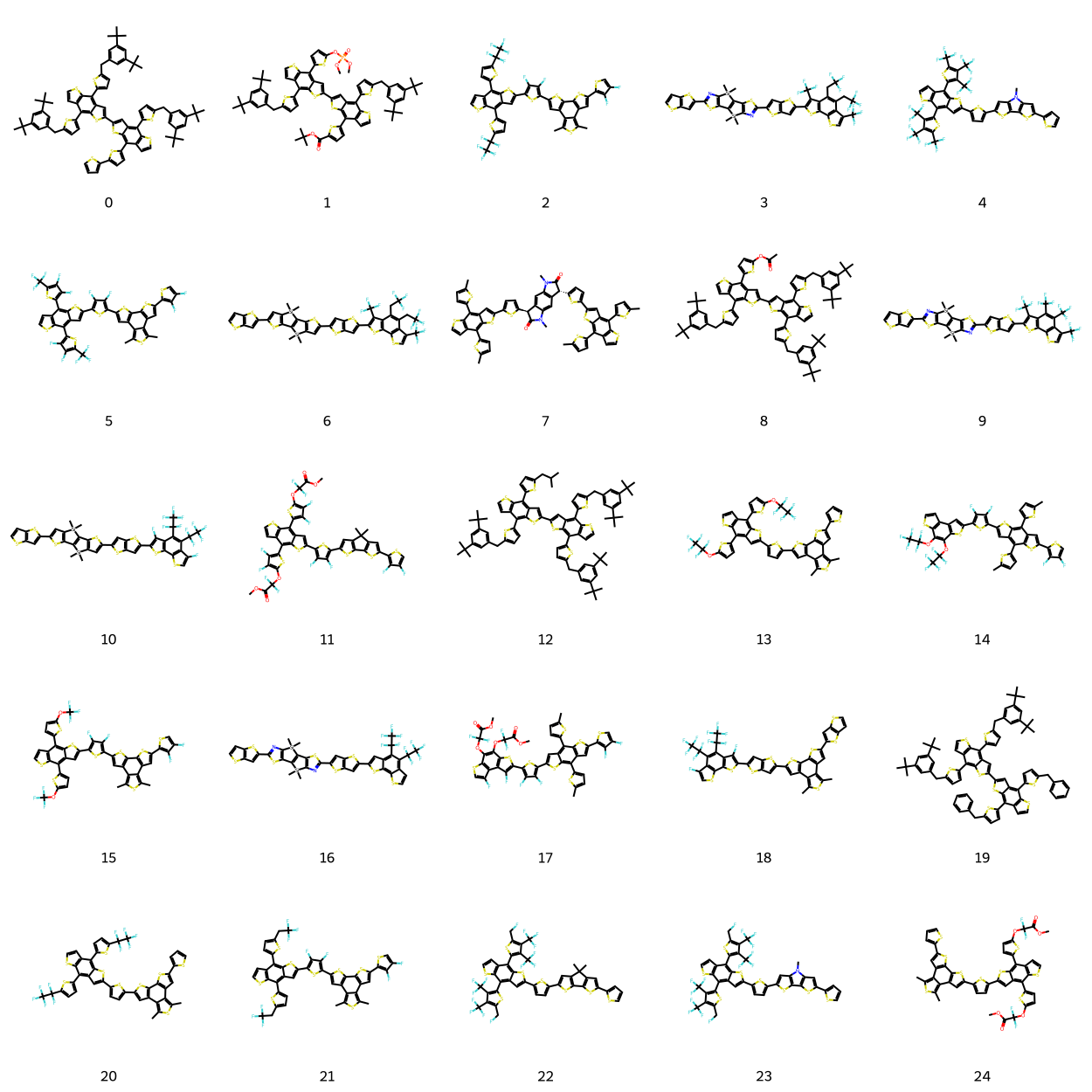
データセットに含まれている分子の構造や目的変数の分布を少し見てみましょう。

# 25分子を grid 形式で可視化（RDKit）
smiles_col = 'smile'

# Mol生成（失敗したSMILESはNoneになる）
mols = []
legends = []
for i, smi in enumerate(df[smiles_col].astype(str).head(25)):
    m = Chem.MolFromSmiles(smi)
    mols.append(m)
    legends.append(f"{i}")

# 表示
img = Draw.MolsToGridImage(
    mols,
    molsPerRow=5,
    subImgSize=(250, 250),
    legends=legends
)
display(img)

いかにも太陽電池用材料って感じです。有機薄膜太陽電池はHOMOが高いドナー分子とLUMOが深いアクセプター分子で構成されていることが多いです。光を当てることで、それらの界面で電荷分離が起こり、ホールは陽極に、電子は陰極に流れることで、電気が発生します。詳しい説明は専門書に譲ります。

それでは、目的変数の一つであるgapの分布を見てみましょう。

# 目的変数の可視化

# 目的変数のselect
target_col = "gap"
if target_col not in df_train.columns:
    raise ValueError(f"'{target_col}' 列がありません。利用可能列: {list(df_train.columns)}")

x = df_train[target_col].dropna()

plt.figure()
plt.hist(x, bins=40)
plt.title("Histogram of gap")
plt.xlabel("gap")
plt.ylabel("count")
plt.show()

print("count:", len(x))
print("min / max:", float(x.min()), float(x.max()))
print("mean / std:", float(x.mean()), float(x.std()))
print("quantiles:", x.quantile([0.01, 0.05, 0.5, 0.95, 0.99]).to_dict())

count: 54335
min / max: 0.5283 5.9262
mean / std: 2.3321466936597037 0.512168096084987
quantiles: {0.01: 1.291238, 0.05: 1.556, 0.5: 2.3128, 0.95: 3.1898299999999997, 0.99: 3.7101659999999996}

最大値が5.9くらいで、最小値は0.53でした。このgapが小さければ小さいほど、長波長側(赤や近赤外)の領域で光を吸収することができます。逆にgapが大きいと短波長側(紫外や青)の領域で光を吸収できます。極端にgapが小さいもの、大きいサンプルは少なく、平均値2.3付近にサンプルが集中しています。

Hold-out split & Robust scaling

GNN実装の前に、データセットを学習、検証、テストに分けましょう。また、論文に合わせてスケーリングも行います。通常の標準化と異なり、中央値とIQRでスケーリングしていました。こちらの方が外れ値に強いそうです。

# ============================================================
# Hold-out split: train / val / test（ランダム分割）
# ============================================================

# まず train と temp に分割（temp は val + test 用）
train_df, temp_df = train_test_split(
    df,
    test_size=0.2,          # 全体の 20% を val + test に回す
    random_state=SEED,
    shuffle=True,
)

# temp を val / test に半分ずつ分割（= 各 10%）
val_df, test_df = train_test_split(
    temp_df,
    test_size=0.5,
    random_state=SEED,
    shuffle=True,
)

# index を詰め直す（後段の Dataset / DataLoader で扱いやすくするため）
train_df = train_df.reset_index(drop=True)
val_df   = val_df.reset_index(drop=True)
test_df  = test_df.reset_index(drop=True)

print(
    "Hold-out split sizes ->",
    "train:", len(train_df),
    "val:", len(val_df),
    "test:", len(test_df),
)

# ============================================================
# Robust scaling: median = 0, IQR = 1（train のみで fit）
# ============================================================
# ・外れ値に強いスケーリング
# ・中央値でセンタリング、四分位範囲 (IQR) でスケール
# ・情報リークを防ぐため、必ず train データのみで fit する

def fit_robust_scaler(y: pd.Series):
    """
    Robust scaler を計算する（中央値・IQR）。
    """
    y = y.astype(float)
    med = float(y.median())
    q1 = float(y.quantile(0.25))
    q3 = float(y.quantile(0.75))
    iqr = q3 - q1
    if iqr == 0:
        iqr = 1.0  # 定数列対策（ゼロ割防止）
    return med, iqr


def transform_robust(y, med, iqr):
    """
    Robust scaling を適用する。
    """
    return (y.astype(float) - med) / iqr


def inverse_robust(y_scaled, med, iqr):
    """
    スケーリングを元の物理量スケールに戻す。
    （評価時に使用）
    """
    return y_scaled * iqr + med


# ---- train データのみで scaler を fit ----
scalers = {col: fit_robust_scaler(train_df[col]) for col in target_cols}

# ---- train / val / test に同じ scaler を適用 ----
train_df = train_df.copy()
val_df   = val_df.copy()
test_df  = test_df.copy()

for col in target_cols:
    med, iqr = scalers[col]
    train_df[f"{col}_scaled"] = transform_robust(train_df[col], med, iqr)
    val_df[f"{col}_scaled"]   = transform_robust(val_df[col],   med, iqr)
    test_df[f"{col}_scaled"]  = transform_robust(test_df[col],  med, iqr)

print("[fit on train] gap median (raw):", scalers["gap"][0], "IQR (raw):", scalers["gap"][1])
print("[after scaling] gap_scaled median:", float(train_df["gap_scaled"].median()))

q1 = float(train_df["gap_scaled"].quantile(0.25))
q3 = float(train_df["gap_scaled"].quantile(0.75))
print("[after scaling] gap_scaled IQR:", q3 - q1)

Hold-out split sizes -> train: 43468 val: 5433 test: 5434
[fit on train] gap median (raw): 2.3118 IQR (raw): 0.664525
[after scaling] gap_scaled median: 0.0
[after scaling] gap_scaled IQR: 1.0

ダウンロード時の分割数と同様に、検証データとテストデータが5000個くらいにになるようにsplitしました。そして、Robust scalingが実行され中央値が0、IQRが1となっています。予測後に出力はinverse_robust関数により逆変換されて、元のスケールに戻ります。

SMILES→PyG Data

GNNに入力するため、SMILES文字列を分子グラフ（PyTorch Geometric Data, PyG)に変換する必要があります。まず、前提条件（特徴量の設計仕様）を定義していきます。

# ----------------------------
# 原子・結合の離散特徴量設定
# ----------------------------

# 原子番号・次数の上限（クリップ用）
MAX_ATOMIC_NUM = 100
MAX_DEGREE = 5

# 結合タイプ（論文中の B 行列選択に対応）
BOND_TYPES = {
    Chem.rdchem.BondType.SINGLE: 0,
    Chem.rdchem.BondType.DOUBLE: 1,
    Chem.rdchem.BondType.TRIPLE: 2,
    Chem.rdchem.BondType.AROMATIC: 3,
}
NUM_BOND_TYPES = 4

# ----------------------------
# 追加の原子特徴量
#  - 形式電荷
#  - 混成軌道
# ----------------------------

# 形式電荷（クリップして離散化）
MIN_FC, MAX_FC = -2, 2
FC_OFFSET = -MIN_FC               # -2..2 → 0..4
NUM_FC = (MAX_FC - MIN_FC + 1)

# 混成軌道タイプ
HYB_MAP = {
    Chem.rdchem.HybridizationType.SP: 0,
    Chem.rdchem.HybridizationType.SP2: 1,
    Chem.rdchem.HybridizationType.SP3: 2,
    Chem.rdchem.HybridizationType.SP3D: 3,
    Chem.rdchem.HybridizationType.SP3D2: 4,
}
HYB_UNKNOWN = 5
NUM_HYB = 6

各変数の説明として、

• MAX_ATOMIC_NUM : 原子番号の上限を設定します（ここでは100）。もしGetAtomicNum()が100より大きい元素になっても、100で丸めます。極端に大きい原子番号をそのまま入れると、Embeddingの語彙（カテゴリ数）が増えすぎるのを防ぐためです。

• MAX_DEGREE : 原子の次数＝「その原子に直接つながっている結合の本数」の上限をクリップします（ここでは5）。有機分子だと、多くは1~4で、5以上はレアです。こちらもカテゴリ数を抑え、レアケースはその他にまとめます。

• BOND_TYPE : RDKitのBondTypeを整数IDに変換する辞書です。これらを0~3の離散カテゴリとして持たせることで、後段でEmbedding(NUM_BOND_TYPES, dim)みたいに埋め込むことでできます。NUM_BOND_TYPE = 4は「bond_typeがとり得るカテゴリ数」です。

• MIN_FC, MAX_FC, FC_OFFSET, NUM_FC : 形式電荷関連の変数で、形式電荷を-2~+2の範囲にクリップして使う設計です。また、FC_OFFSET = -(-2) = 2なので、
  • -2 → 0
  • -1 → 1
  • 0 → 2
  • +1 → 3
  • +2 → 4
    のように非負整数に変換できます。よって、NUM_FC = 5は「形式電荷がとり得るカテゴリ数」となります。形式電荷は負になり得るので、そのままだとEmbeddingのindexに使いづらいので、このような変換を行っています。

• HYB_MAP, HYB_UNKNOWN, NUM_HYB : 混成関連の変数です。HYB_MAPはRDKitのatom.GetHybridization()が返す種類を整数ID化する辞書になります。対応していない混成が来たときは、HYB_UNKNOWN = 5に落とします。よって、NUM_HYB = 6となります。

次にこれらの前提条件を使用して、特徴量を抽出し、smileをPyGに変換する関数群を定義します。

この関数はノード特徴量を抽出する関数です。

def atom_features_v2(atom: Chem.rdchem.Atom) -> torch.Tensor:
    """
    原子特徴量（すべて離散値）
    x[:, :] の各列の意味：
      x[:,0]: 原子番号（クリップあり）
      x[:,1]: 原子次数（クリップあり）
      x[:,2]: 芳香族フラグ（0/1）
      x[:,3]: 形式電荷（-2..2 を 0..4 に変換）
      x[:,4]: 混成軌道タイプ
    """
    atomic_num = min(atom.GetAtomicNum(), MAX_ATOMIC_NUM)
    degree = min(atom.GetDegree(), MAX_DEGREE)
    aromatic = int(atom.GetIsAromatic())

    # 形式電荷をクリップしてオフセット
    formal_charge = atom.GetFormalCharge()
    formal_charge = max(MIN_FC, min(formal_charge, MAX_FC)) + FC_OFFSET  # 0..NUM_FC-1

    # 混成軌道（未知は HYB_UNKNOWN）
    hyb_idx = HYB_MAP.get(atom.GetHybridization(), HYB_UNKNOWN)

    return torch.tensor([atomic_num, degree, aromatic, formal_charge, hyb_idx], dtype=torch.long)

RDKitのAtomオブジェクトを受け取り、PyTorchのテンソル（long型）で特徴量を返す関数です。

atom.GetAtomicNum()で原子番号（C=6など）を取得し、atom.GetDegree()で次数（結合の本数）を取得します。また、芳香族かどうかをatom.GetIsAromatic()でTrue/Falseで受け取り、0/1に変換しています。atom.GetFormalCharge()で形式電荷を取得します。そして、RDKitが返す混成タイプをHYB_MAPで整数化しています。最後に、取得した5個の離散特徴量をtorch.long（整数）テンソルで返しています。

次にエッジ特徴量を抽出する関数を定義します。

def bond_features(bond: Chem.rdchem.Bond) -> torch.Tensor:
    """
    結合特徴量（離散）
    edge_attr[:, :] の各列の意味：
      edge_attr[:,0]: 結合タイプ（SINGLE/DOUBLE/TRIPLE/AROMATIC）
      edge_attr[:,1]: 共役フラグ（0/1）
      edge_attr[:,2]: 環内結合フラグ（0/1）
    """
    bond_type = BOND_TYPES.get(bond.GetBondType(), 0)
    conjugated = int(bond.GetIsConjugated())
    in_ring = int(bond.IsInRing())
    return torch.tensor([bond_type, conjugated, in_ring], dtype=torch.long)

bond.GetBondType()でsingle/double/triple/aromaticのどれかを返して、それを辞書に落とします。bond.GetIsConjugated()で共役結合かどうかを0/1で取得し、bond.IsInRing()でその結合が環の一部かどうかを0/1で取得しています。最後に、これら3要素テンソルとして返します。

ノードとエッジの特徴を抽出できるようになったので、これらを使いsmilesをPyGに変換する関数を定義します。

def smiles_to_pyg_v2(smiles: str, y_values: list):
    """
    SMILES 文字列を PyG の Data オブジェクトに変換する
    """

    mol = Chem.MolFromSmiles(smiles)
    if mol is None:
        return None

    # ----------------------------
    # ノード特徴量
    # ----------------------------
    x = torch.stack([atom_features_v2(a) for a in mol.GetAtoms()], dim=0)  # [num_nodes, 5]

    # ----------------------------
    # エッジ（無向グラフ → 両方向に追加）
    # ----------------------------
    edge_index_list = []
    edge_attr_list = []

    for bond in mol.GetBonds():
        i = bond.GetBeginAtomIdx()
        j = bond.GetEndAtomIdx()
        bf = bond_features(bond)

        edge_index_list.append([i, j])
        edge_attr_list.append(bf)
        edge_index_list.append([j, i])
        edge_attr_list.append(bf)

    # 結合が存在しない分子への保険
    if len(edge_index_list) == 0:
        edge_index = torch.empty((2, 0), dtype=torch.long)
        edge_attr = torch.empty((0, 3), dtype=torch.long)
    else:
        edge_index = torch.tensor(edge_index_list, dtype=torch.long).t().contiguous()
        edge_attr = torch.stack(edge_attr_list, dim=0)

     # 目的変数（8タスク）
    y = torch.tensor(y_values, dtype=torch.float).view(1, -1)  # [1, 8]
    data = Data(x=x, edge_index=edge_index, edge_attr=edge_attr, y=y)
    data.smiles = smiles

    return data

smileと8個の目的変数（scaled）を受け取り、PyGのDataにして返す関数です。

mol.GetAtoms()で全原子を列挙し、各原子に先ほどのatom_features_v2を適用することで、5要素テンソルが返ってきます。それらをstackして形状[num_nodes, 5]のノード特徴量テンソルxにします。num_nodesはそのグラフ（分子）に含まれるノード数のことで、ここでは、ノード＝原子となります。つまり、分子中の原子数です。atom_features_v2は原子ごとに適用されています。例えば、ベンゼンの場合、炭素原子が6個あるので、x.shape=[6,5]となります。

次に、forループで分子内の全結合を列挙し、bond.GetBeginAtomIdx()とbond.GetEndAtomIdx()を使い、結合の両端の原子indexを取得します（0~num_nodes-1）。そして先に定義したbond_featuresを使って結合特徴（3要素）をテンソルで用意します。

edge_index_listは[ [i,j], [j,i], ... ]なので、テンソル化すると形状[num_edges, 2]です。.t() で転置してPyG標準の[2, num_edges]にします。.contiguous()はメモリ連続化（PyGや後段の演算で安全）のためです。ここの2という数字は、「エッジを構成するノードindexが2つある（from, to）」ことを表しています。

num_edgesはグラフ中のエッジ（辺）の数のことで、分子グラフでは、エッジ＝原子同士の結合になります。ただし、PyGの場合は有向エッジで数えます。「i→j」と「j→i」の両方を入れる必要があるということです。C-C結合は1本と考えるのが無向であるのに対して、有向の場合、C→C, C←Cと捉えて1つの結合を2本のエッジとして扱います。

edge_attrは結合特徴（3要素）を stack して形状[num_edges, 3]となります。

例えばベンゼンの場合、C-C結合は6本ですが、各結合を両方向にするので、num_edges = 6*2 = 12となります。よって、edge_index=[2, 12], edge_atrr=[12, 3]となるわけです。

これらを目的変数yと共にDataへ格納し、Data(x, edge_index, edge_attr, y)の形で返します。

smilesをPyGへ変換できるようになったので、GNNが食えるようにDataset化を行います。

class SmilesGraphDataset(Dataset):
    """
    DataFrame（SMILES + 目的変数）から
    PyG Data のリストを作る Dataset
    """
    def __init__(self, df: pd.DataFrame):
        self.data_list = []
        bad = 0

        scaled_cols = [f"{col}_scaled" for col in target_cols]

        for idx, row in df.iterrows():
            smi = row["smile"]
            y_vals = [row[col] for col in scaled_cols]  # 8つのscaled値
            d = smiles_to_pyg_v2(smi, y_vals)  # yをリストで渡す
            if d is None:
                bad += 1
            else:
                self.data_list.append(d)

        print(f"Converted graphs: {len(self.data_list)} / {len(df)} (invalid smiles removed: {bad})")

    def __len__(self):
        return len(self.data_list)

    def __getitem__(self, idx):
        return self.data_list[idx]


# --- Build datasets from scaffold split ---
train_dataset = SmilesGraphDataset(train_df)
val_dataset   = SmilesGraphDataset(val_df)
test_dataset  = SmilesGraphDataset(test_df)

# quick check
d0 = train_dataset[0]
print(d0)
print("y:", d0.y)  # [8]

Converted graphs: 43468 / 43468 (invalid smiles removed: 0)
Converted graphs: 5433 / 5433 (invalid smiles removed: 0)
Converted graphs: 5434 / 5434 (invalid smiles removed: 0)
Data(x=[27, 5], edge_index=[2, 62], edge_attr=[62, 3], y=[1, 8], smiles='COC(=O)c1nc2c(-c3ccc(-c4cccs4)s3)sc(-c3cccs3)c2o1')
y: tensor([[-0.0611,  0.2469, -0.0186, -0.0455,  0.5954, -0.0470, -0.5580,  0.0504]])

forループで、DataFrameを1行ずつ読み、smiles_to_pvg_v2に渡して、PyGのDataを生成、self.data_listに貯めていきます。

そして、各DataFrameをDatasetに変換し、train_datasetの「0番目の分子グラフ」の中身を表示しています。

x=[27, 5]は、原子数が27個、原子特徴量の次元が5（先に設計した5項目）ということです。
edge_index=[2, 62]は、62本のエッジがあり、ノードindexが2つあるということ。
edge_attr=[62, 3]は、62本のエッジそれぞれに3特徴が入っているということになります。

最後にbatch処理を行うため、今定義したDatasetをDataLoaderにします。

# DataLoader + sanity check

batch_size = 32

train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
val_loader   = DataLoader(val_dataset,   batch_size=batch_size, shuffle=False)
test_loader  = DataLoader(test_dataset,  batch_size=batch_size, shuffle=False)

# 1バッチ取り出して形確認
batch = next(iter(train_loader))
print(batch)

print("batch.x:", batch.x.shape)               # [total_nodes_in_batch, 5]
print("batch.edge_index:", batch.edge_index.shape)
print("batch.edge_attr:", batch.edge_attr.shape)
print("batch.y:", batch.y.shape)               # [num_graphs] （通常は64）
print("batch.batch:", batch.batch.shape)       # [total_nodes_in_batch]
print("num_graphs:", batch.num_graphs)

# GPUに乗せてみる（エラー出ないか確認）
batch = batch.to(device)
print("moved to device OK")

DataBatch(x=[1312, 5], edge_index=[2, 3032], edge_attr=[3032, 3], y=[32, 8], smiles=[32], batch=[1312], ptr=[33])
batch.x: torch.Size([1312, 5])
batch.edge_index: torch.Size([2, 3032])
batch.edge_attr: torch.Size([3032, 3])
batch.y: torch.Size([32, 8])
batch.batch: torch.Size([1312])
num_graphs: 32
moved to device OK

batch_size=32としているので、PyGのDataLoaderはtrain_dataset[i]（1分子＝1グラフ）を32個集めて、1つのDataBatchオブジェクトにまとめています。重要なポイントしては、「32個の小さなグラフ」を「1つの巨大のグラフ」として結合している点です。

つまり、train_loaderから取り出した以下のbatchは、

DataBatch(
  x=[1312, 5],
  edge_index=[2, 3032],
  edge_attr=[3032, 3],
  y=[32, 8],
  smiles=[32],
  batch=[1312],
  ptr=[33]
)

32分子合計で、1312個の原子、3032本の有向エッジが存在していることを示しています。32分子の情報をまとめてしまうと、1つ1つの分子の情報が埋もれてしまうのではと疑問を抱くかもしれませんが、PyGはbatch.batchにより、各ノードが「どの分子に属しているか」をきちんと管理しています。

例として、

batch.batch = [0,0,0,0,1,1,1,1,1,2,2,2,...]

のように、先頭の数個の原子は分子0、次の原子群は分子1といった感じです。これができるからこそ、後程出てくるglobal_add_poolにより分子単位の集約ができるため、1分子に対して8個の目的変数を対応させることができます。

GNN実装

いよいよGNNを作っていきましょう。論文の構成は以下の通りです。

• 埋め込み層
• Message passing層
• Readout層
• 全結合層

それでは、実装していきましょう。まず、Message passing部分を実装します。

class EdgeCondLinearLayer(MessagePassing):
    """
    論文の (B) に対応：
      m_{ij} = W_{bond_type} h_j
    を作ってから、GRUでノード状態を更新する層。
    """
    def __init__(self, hidden_dim: int, num_bond_types: int):
        super().__init__(aggr="add")  # 近傍メッセージを加算で集約
        self.hidden_dim = hidden_dim
        self.num_bond_types = num_bond_types

        # 結合タイプごとの重み行列 W_e: [T, H, H]
        self.W = nn.Parameter(torch.empty(num_bond_types, hidden_dim, hidden_dim))
        nn.init.xavier_uniform_(self.W)

        # GRU: input=message, hidden=old_state
        self.gru = nn.GRUCell(hidden_dim, hidden_dim)

    def forward(self, x, edge_index, bond_type):
        """
        x        : [N, H]  ノード表現
        edge_index: [2, E] 有向エッジ
        bond_type : [E]    エッジごとの結合タイプ（0..T-1）
        """
        # propagate() は message() を呼び、aggr="add" でノードごとに集約する
        m = self.propagate(edge_index, x=x, bond_type=bond_type)  # [N, H]

        # GRUで更新（input=m, hx=x）
        x_out = self.gru(m, x)  # [N, H]
        return x_out

    def message(self, x_j, bond_type):
        """
        x_j      : [E, H]  エッジの送信元ノード表現（j側）
        bond_type: [E]     結合タイプ
        """
        bt = bond_type.clamp(0, self.num_bond_types - 1)  # 安全のため範囲に収める

        # エッジごとに W_{bt} を選ぶ → [E, H, H]
        W_bt = self.W[bt]

        # m_ij = W_{bt} @ h_j
        m = torch.bmm(W_bt, x_j.unsqueeze(-1)).squeeze(-1)  # [E, H]
        return m

このEdgeCondLinearLayerクラスは、「結合タイプに応じて異なる線形変換を使い、近傍原子からメッセージを集め、GRUで原子表現を更新する」という処理を1ステップ分行います。この層をM=3重ねることで、原子は最大3ホップ先の化学環境を考慮した表現になります。

EdgeCondLinearLayer.forward()を1回呼ぶと、PyGの中で次のことが自動的に置きます。

forward（1回）
 └─ propagate（1回）
     ├─ message（エッジごとに E 回）
     └─  aggregate（ノードごとに N 回）

それぞれ何が起こっているかというと、

①forward : 層として1回

def forward(self, x, edge_index, bond_type):
        """
        x        : [N, H]  ノード表現
        edge_index: [2, E] 有向エッジ
        bond_type : [E]    エッジごとの結合タイプ（0..T-1）
        """
        # propagate() は message() を呼び、aggr="add" でノードごとに集約する
        m = self.propagate(edge_index, x=x, bond_type=bond_type)  # [N, H]

        # GRUで更新（input=m, hx=x）
        x_out = self.gru(m, x)  # [N, H]
        return x_out

• 粒度：層全体で1回
• 対象：全ノード、全エッジ
• 役割：Message passingを実行、集約結果を使ってノード状態を更新する

⇒「この層を1ステップ進める」操作になります。

②message : エッジごと

def message(self, x_j, bond_type):
        """
        x_j      : [E, H]  エッジの送信元ノード表現（j側）
        bond_type: [E]     結合タイプ
        """
        bt = bond_type.clamp(0, self.num_bond_types - 1)  # 安全のため範囲に収める

        # エッジごとに W_{bt} を選ぶ → [E, H, H]
        W_bt = self.W[bt]

        # m_ij = W_{bt} @ h_j
        m = torch.bmm(W_bt, x_j.unsqueeze(-1)).squeeze(-1)  # [E, H]
        return m

• 粒度：エッジ単位（E回）
• 対象：各有向エッジj→i
• 役割：このエッジを通して、どんな情報を送るかを決める

⇒ここでは、ノード更新はせず、送信メッセージを送るだけになります。

③aggregate : ノードごと（PyG内部）

def __init__(self, hidden_dim: int, num_bond_types: int):
        super().__init__(aggr="add")  # 近傍メッセージを加算で集約

• 粒度：ノード単位（N回）
• 出力：m（shape [N, H]）

agge='add'とすることで、先ほどのmのΣをとります。

④GRU更新：ノードごと（明示的）

x_out = self.gru(m, x)

• 粒度：ノード単位（N個まとめて計算）
• 各ノードについて：

⇒ここで、ノード更新が行われます。

---

◎イメージが湧きにくいと思うので、ベンゼンで直感的に考えてみます。

最初の入力は、

h.shape = [N, H] = [6, 128]
edge_index.shape = [2, 12]
bond_type.shape = [12]

となります。x[i]は原子 i (炭素）の現在のベクトルで埋め込み後は128次元の初期状態h[i]となります。この時点では、「自分自身の特徴＋初期埋め込み」しか持っていません。

次に、

(1) message : エッジごと（12回）
各有向エッジj→iについて：

m_ij = A_{bond_type(j,i)} h_j

ベンゼンの場合は全結合がaromaticなので、A_aromaticが12回使われます(i→j, j→i)。そして出力は、

m.shape = [12, 128]

となります。

(2) aggregate : ノードごと（6回）
各原子 i について：

m_i = Σ_{j ∈ 隣接原子} m_ij

ベンゼンの場合、各炭素は隣接原子が2つあるので、2つのメッセージを足します。結果、

m.shape = [6, 128]

となるわけです。

(3) GRU更新：ノードごと（6回）

h_i^{new} = GRU(m_i, h_i)

新しい情報（隣接原子由来）と古い情報（自分自身）を混ぜた更新後の原子ベクトルが得られます。結果、

x_out.shape = [6, 128]

となり、最初と形状は変わらないのですが、中身は「1ホップ先（隣の原子）の情報」を取り込んだ表現となります。

---

EdgeCondLinearLayerで「1回分の message passing」を実装できたので、次はそれを 3回繰り返し、分子全体の表現から 8つの物性を同時回帰するネットワークを組みます。

class MPNNRegressor(nn.Module):
    """
    論文準拠の構成（要点）：
      - ノード隠れ次元: 128
      - Message Passing 回数: M=3（num_layers）
      - 分子fingerprint: 1024次元（和集合=ノード和）
      - Head: (BN+ReLU付き) 1024 -> 512 -> 256 -> out
    """
    def __init__(
        self,
        hidden_dim: int = 128,
        num_layers: int = 3,
        num_targets: int = 8,
        dropout: float = 0.0,     # 論文が指定していればここで使用
    ):
        super().__init__()

        # ----------------------------
        # (1) ノード特徴の埋め込み（離散特徴 → embedding → concat）
        # ----------------------------
        self.emb_atomic = nn.Embedding(MAX_ATOMIC_NUM + 1, 64)
        self.emb_degree = nn.Embedding(MAX_DEGREE + 1, 16)
        self.emb_aroma  = nn.Embedding(2, 8)
        self.emb_fc     = nn.Embedding(NUM_FC, 8)
        self.emb_hyb    = nn.Embedding(NUM_HYB, 8)

        node_in_dim = 64 + 16 + 8 + 8 + 8  # = 104
        self.node_proj = nn.Linear(node_in_dim, hidden_dim)  # 104 -> 128

        # ----------------------------
        # (2) Message Passing 層（B: bond-type別行列 + GRU更新）
        # ----------------------------
        self.layers = nn.ModuleList([
            EdgeCondLinearLayer(hidden_dim=hidden_dim, num_bond_types=NUM_BOND_TYPES)
            for _ in range(num_layers)  # M = num_layers
        ])

        # ----------------------------
        # (3) Readout: ノード -> 1024 次元に写像してから sum pool
        #     fingerprint g ∈ R^{1024}
        # ----------------------------
        self.fp_dim = 1024
        self.node_to_fp = nn.Linear(hidden_dim, self.fp_dim)

        # ----------------------------
        # (4) Head: 1024 -> 512 -> 256 -> out（BN + ReLU）
        # ----------------------------
        self.fc1 = nn.Linear(self.fp_dim, 512)
        self.bn1 = nn.BatchNorm1d(512)

        self.fc2 = nn.Linear(512, 256)
        self.bn2 = nn.BatchNorm1d(256)

        self.out = nn.Linear(256, num_targets)

        self.dropout = dropout

    def forward(self, data):
        """
        data.x        : [N, 5]  (long) 原子の離散特徴
        data.edge_index: [2, E]
        data.edge_attr : [E, 3] (long) 結合特徴（0列目が bond_type）
        data.batch     : [N]    各ノードが属するグラフID
        """
        x = data.x
        edge_index = data.edge_index
        edge_attr  = data.edge_attr
        batch      = data.batch

        # ----------------------------
        # ノード埋め込み（v2: 5特徴）
        # ----------------------------
        atomic_num      = x[:, 0].clamp(0, MAX_ATOMIC_NUM)
        degree          = x[:, 1].clamp(0, MAX_DEGREE)
        aromatic        = x[:, 2].clamp(0, 1)
        formal_charge   = x[:, 3].clamp(0, NUM_FC - 1)
        hybridization   = x[:, 4].clamp(0, NUM_HYB - 1)

        h = torch.cat([
            self.emb_atomic(atomic_num),
            self.emb_degree(degree),
            self.emb_aroma(aromatic),
            self.emb_fc(formal_charge),
            self.emb_hyb(hybridization),
        ], dim=-1)                       # [N, 104]

        h = self.node_proj(h)            # [N, 128]

        # ----------------------------
        # bond_type（行列選択に使う）
        # ----------------------------
        bond_type = edge_attr[:, 0].clamp(0, NUM_BOND_TYPES - 1)  # [E]

        # ----------------------------
        # Message Passing（M回）
        # ----------------------------
        for layer in self.layers:
            h = layer(h, edge_index, bond_type)  # [N, 128]

        # ----------------------------
        # Readout: 1024-d fingerprint
        # 1) ノード表現を 1024次元に写像
        # 2) 分子ごとに sum pool（global_add_pool）
        # ----------------------------
        h_fp = self.node_to_fp(h)                 # [N, 1024]
        g    = global_add_pool(h_fp, batch)       # [B, 1024]  (B = num_graphs)

        # ----------------------------
        # Head: 1024 -> 512 -> 256 -> out
        # （各層 BatchNorm + ReLU）
        # ----------------------------
        z = self.bn1(self.fc1(g))
        z = F.relu(z)
        if self.dropout > 0:
            z = F.dropout(z, p=self.dropout, training=self.training)

        z = self.bn2(self.fc2(z))
        z = F.relu(z)
        if self.dropout > 0:
            z = F.dropout(z, p=self.dropout, training=self.training)

        out = self.out(z)                         # [B, num_targets]
        return out

この MPNNRegressor は、大きく 4ブロックで構成されています。

(1) 原子特徴（離散値）を埋め込みして 128次元へ
入力 data.x は [N, 5]（Nはバッチ内の総原子数）で、各列は、

• 原子番号 / 次数 / 芳香族フラグ / 形式電荷 / 混成

の 離散値です。これらをそれぞれ Embedding に通して連結し、最後に線形変換で 128次元（hidden_dim） に揃えます。コードでいうと、下記に当たります。

# ----------------------------
# (1) ノード特徴の埋め込み（離散特徴 → embedding → concat）
# ----------------------------
self.emb_atomic = nn.Embedding(MAX_ATOMIC_NUM + 1, 64)
self.emb_degree = nn.Embedding(MAX_DEGREE + 1, 16)
self.emb_aroma  = nn.Embedding(2, 8)
self.emb_fc     = nn.Embedding(NUM_FC, 8)
self.emb_hyb    = nn.Embedding(NUM_HYB, 8)

node_in_dim = 64 + 16 + 8 + 8 + 8  # = 104
self.node_proj = nn.Linear(node_in_dim, hidden_dim)  # 104 -> 128

これにより、

data.x: [N, 5]  →  h: [N, 128]

となります。

(2) message passingをM=3回繰り返す

EdgeCondLinearLayerをModuleListで3回作り、順に適用します。コードでいうと、この部分です。

# ----------------------------
# (2) Message Passing 層（B: bond-type別行列 + GRU更新）
# ----------------------------
self.layers = nn.ModuleList([
        EdgeCondLinearLayer(hidden_dim=hidden_dim, num_bond_types=NUM_BOND_TYPES)
        for _ in range(num_layers)  # M = num_layers
    ])

形状は変わりませんが、各ノード表現hの中身は更新され、原子が最大3ホップ先の化学環境を反映した表現になります。

h: [N, 128] → (MP ×3) → h: [N, 128]

(3) Readout : 最終隠れ状態から分子fingerprint（1024次元）を作る

論文では、readout は 最終隠れ状態のみを用いて分子全体の特徴ベクトル ŷ（1024次元）を作っています。

ここでは、

1. ノード表現を Linear(128→1024) で写像
2. 分子ごとにノード和をとる（global_add_pool）

という形で 集合（set）としての分子表現を作ります。

# ----------------------------
# Readout: 1024-d fingerprint
# 1) ノード表現を 1024次元に写像
# 2) 分子ごとに sum pool（global_add_pool）
# ----------------------------
h_fp = self.node_to_fp(h)                 # [N, 1024]
g    = global_add_pool(h_fp, batch)       # [B, 1024]  (B = num_graphs)

これにより、

h: [N, 128] → h_fp: [N, 1024] → g: [B, 1024]

となります。Bはバッチ内の分子数（=num_graphs）です。

(4) Head：1024 → 512 → 256 → 出力（BN + ReLU）

# ----------------------------
# (4) Head: 1024 -> 512 -> 256 -> out（BN + ReLU）
# ----------------------------
self.fc1 = nn.Linear(self.fp_dim, 512)
self.bn1 = nn.BatchNorm1d(512)

self.fc2 = nn.Linear(512, 256)
self.bn2 = nn.BatchNorm1d(256)

self.out = nn.Linear(256, num_targets)

論文通り、fingerprint g を

• 全結合（512）→ BatchNorm → ReLU
• 全結合（256）→ BatchNorm → ReLU

に通して、最後に各物性予測に対応する出力層へ接続します。

g: [B, 1024] → [B, 512] → [B, 256] → out: [B, 8]

このout([B,8])とdata.y([B,8])で損失を計算して、マルチタスク回帰として学習することができます。

やっとGNNが実装できたので、さっそく学習させましょう。
一回コーヒーブレイクもありです☕

GNN学習・評価

学習に関しては他のNNと同様に、学習の条件を設定し実行するだけです。

# --- 損失関数 ---
# マルチタスク回帰（8物性）なので、各要素の MSE の平均をとる
criterion = nn.MSELoss()

# --- 最適化手法 ---
# 論文で最良とされている学習率 1e-3 の Adam
optimizer = torch.optim.Adam(
    model.parameters(),
    lr=1e-3,
    weight_decay=0.0
)

# --- 学習率スケジューラ ---
# 論文の「エポックごとに 2×10^-6 の減衰」を
# 指数減衰として解釈し、epoch ごとに lr を少しずつ下げる
#   lr_{t+1} = lr_t * (1 - 2e-6)
decay = 2e-6
scheduler = torch.optim.lr_scheduler.LambdaLR(
    optimizer,
    lr_lambda=lambda epoch: (1.0 - decay) ** epoch
)


def train_one_epoch(model, loader, optimizer, criterion, device):
    """
    1エポック分の学習を行う関数

    Returns
    -------
    train_mse : float
        分子あたり平均 MSE（scaled 空間）
    train_mae : float
        分子あたり平均 MAE（scaled 空間、8物性平均）
    """
    model.train()
    total_loss = 0.0
    total_mae = 0.0
    n = 0  # 分子数カウント

    for batch in tqdm(loader, desc="train", leave=False):
        batch = batch.to(device)

        # 勾配の初期化
        optimizer.zero_grad()

        # --- 順伝播 ---
        pred = model(batch)        # [B, 8]（scaled）
        y = batch.y.float()        # [B, 8]（scaled）

        # --- 損失計算 ---
        loss = criterion(pred, y)

        # --- 逆伝播 & 更新 ---
        loss.backward()
        optimizer.step()

        # --- MAE を参考指標として計算 ---
        with torch.no_grad():
            mae = torch.mean(torch.abs(pred - y))

        bsz = batch.num_graphs
        total_loss += loss.item() * bsz
        total_mae  += mae.item()  * bsz
        n += bsz

    return total_loss / n, total_mae / n


@torch.no_grad()
def evaluate_scaled(model, loader, device, target_cols):
    """
    scaled 空間での評価

    Returns
    -------
    results : dict
        {target: {mae, rmse, r2}}
    """
    model.eval()
    preds, ys = [], []

    for batch in tqdm(loader, desc="eval_scaled", leave=False):
        batch = batch.to(device)
        pred = model(batch).cpu()   # [B, 8]
        y = batch.y.cpu()           # [B, 8]
        preds.append(pred)
        ys.append(y)

    preds = torch.cat(preds, dim=0)  # [N, 8]
    ys    = torch.cat(ys, dim=0)     # [N, 8]

    results = {}
    for i, col in enumerate(target_cols):
        resid = preds[:, i] - ys[:, i]

        mae = resid.abs().mean().item()
        rmse = torch.sqrt((resid ** 2).mean()).item()

        # 決定係数 R^2
        y_mean = ys[:, i].mean()
        ss_tot = torch.sum((ys[:, i] - y_mean) ** 2)
        ss_res = torch.sum(resid ** 2)
        r2 = (1.0 - ss_res / (ss_tot + 1e-12)).item()

        results[col] = {"mae": mae, "rmse": rmse, "r2": r2}

    return results


@torch.no_grad()
def evaluate_raw(model, loader, device, target_cols, scalers):
    """
    元のスケール（robust scaling を逆変換）での評価

    Returns
    -------
    results : dict
        {target: {mae, rmse, r2}}
    """
    model.eval()
    preds, ys = [], []

    for batch in tqdm(loader, desc="eval_raw", leave=False):
        batch = batch.to(device)
        pred = model(batch).cpu()   # scaled
        y = batch.y.cpu()           # scaled
        preds.append(pred)
        ys.append(y)

    preds = torch.cat(preds, dim=0)
    ys    = torch.cat(ys, dim=0)

    results = {}
    for i, col in enumerate(target_cols):
        med, iqr = scalers[col]

        # robust scaling の逆変換
        pred_raw = preds[:, i] * iqr + med
        y_raw    = ys[:, i] * iqr + med

        resid = pred_raw - y_raw
        mae = resid.abs().mean().item()
        rmse = torch.sqrt((resid ** 2).mean()).item()

        y_mean = y_raw.mean()
        ss_tot = torch.sum((y_raw - y_mean) ** 2)
        ss_res = torch.sum(resid ** 2)
        r2 = (1.0 - ss_res / (ss_tot + 1e-12)).item()

        results[col] = {"mae": mae, "rmse": rmse, "r2": r2}

    return results


def results_to_df(results: dict, title: str):
    """
    評価結果を DataFrame にまとめて表示
    """
    dfm = pd.DataFrame(results).T
    dfm.index.name = "target"
    dfm = dfm[["mae", "rmse", "r2"]]
    print(f"\n[{title}]")
    print(dfm)
    return dfm

学習の基本方針として、

• 8物性値のマルチタスク回帰として学習
• 損失関数はscaled空間でのMSE
• OptimizerはAdam(lr=1e-3)（論文で最良と報告）

としています。

学習率スケジューリングは、論文には、
Explicit learning rate decay was also noticed to improve optimization, a decay value of 2E-6 each epoch was used.
と書かれており、本実装ではこれを「エポックごとの指数減衰」として解釈し、

​

を LambdaLR で実装しています。これにより、epoch単位でわずかに学習率が下がる挙動になります。

評価方法として、

• scaled空間（def evaluate_scaled）⇒ 学習の安定性・モデル比較用
• raw空間（def evaluate_raw）⇒ 実際の物性値としての性能評価

としており、各物性について、MAE, RMSE, R^2を計算しました。

これらの設定で学習・評価させていきます。

# 最大エポック数（論文では 500）
max_epochs = 500

# early stopping の patience
# 指標が改善しないエポックがこれだけ続いたら打ち切り
patience = 20

# early stopping / モニタリングに使う物性と指標
monitor_col = "gap"    # 例: "homo", "lumo"
monitor_key = "rmse"   # "rmse" または "mae"

best_metric = float("inf")
best_state = None
bad_epochs = 0

# 学習ログ保存用（後で可視化する場合など）
history = []

for epoch in range(1, max_epochs + 1):

    # ----------------------------
    # 1) Train（1エポック）
    # ----------------------------
    train_mse, train_mae = train_one_epoch(
        model, train_loader, optimizer, criterion, device
    )

    # ----------------------------
    # 2) Validation（scaled 空間）
    # ----------------------------
    val_scaled = evaluate_scaled(
        model, val_loader, device, target_cols
    )

    # early stopping 判定に使う指標
    current = val_scaled[monitor_col][monitor_key]

    # ----------------------------
    # 3) 学習率減衰（epoch ごとに1回）
    # ----------------------------
    scheduler.step()
    lr = optimizer.param_groups[0]["lr"]

    # ----------------------------
    # 4) ログ出力（代表的な3物性）
    # ----------------------------
    gap_res  = val_scaled["gap"]
    homo_res = val_scaled["homo"]
    lumo_res = val_scaled["lumo"]

    print(
        f"[Epoch {epoch:03d}] lr={lr:.2e} "
        f"train_MSE={train_mse:.4f} train_MAE={train_mae:.4f} | "
        f"VAL gap_RMSE={gap_res['rmse']:.4f} gap_MAE={gap_res['mae']:.4f} gap_R2={gap_res['r2']:.4f} | "
        f"VAL homo_RMSE={homo_res['rmse']:.4f} homo_MAE={homo_res['mae']:.4f} homo_R2={homo_res['r2']:.4f} | "
        f"VAL lumo_RMSE={lumo_res['rmse']:.4f} lumo_MAE={lumo_res['mae']:.4f} lumo_R2={lumo_res['r2']:.4f}"
    )

    # ログ保存
    history.append({
        "epoch": epoch,
        "lr": lr,
        "train_mse": train_mse,
        "train_mae": train_mae,
        "val_gap_rmse": gap_res["rmse"],
        "val_homo_rmse": homo_res["rmse"],
        "val_lumo_rmse": lumo_res["rmse"],
    })

    # ----------------------------
    # 5) Early stopping
    # ----------------------------
    if current < best_metric - 1e-6:
        best_metric = current
        best_state = copy.deepcopy(model.state_dict())
        bad_epochs = 0
    else:
        bad_epochs += 1
        if bad_epochs >= patience:
            print(
                f"Early stopping triggered "
                f"(patience={patience}). "
                f"Best VAL {monitor_col}_{monitor_key}={best_metric:.4f}"
            )
            break

# ----------------------------
# 6) 最良モデルを復元
# ----------------------------
if best_state is not None:
    model.load_state_dict(best_state)

model.to(device).eval()

# （任意）復元後に Validation を再評価
val_scaled_best = evaluate_scaled(
    model, val_loader, device, target_cols
)

print("\n===== BEST MODEL: VAL (scaled) =====")
print(
    f"monitor: {monitor_col}_{monitor_key} = "
    f"{val_scaled_best[monitor_col][monitor_key]:.4f}"
)

# ============================================================
# 7) Final evaluation on TEST（scaled + raw）
# ============================================================

# --- Test（scaled 空間） ---
test_scaled = evaluate_scaled(
    model, test_loader, device, target_cols
)

# --- Test（元スケール） ---
test_raw = evaluate_raw(
    model, test_loader, device, target_cols, scalers
)

print("\n===== FINAL TEST (scaled space) =====")
for k in ["gap", "homo", "lumo"]:
    print(k, test_scaled[k])

print("\n===== FINAL TEST (raw space) =====")
for k in ["gap", "homo", "lumo"]:
    print(k, test_raw[k])

# 表形式でまとめて表示
test_scaled_df = results_to_df(test_scaled, "TEST scaled metrics")
test_raw_df    = results_to_df(test_raw,    "TEST raw metrics")

[Epoch 001] lr=1.00e-03 train_MSE=0.1358 train_MAE=0.2709 | VAL gap_RMSE=0.2721 gap_MAE=0.1991 gap_R2=0.8786 | VAL homo_RMSE=0.2115 homo_MAE=0.1527 homo_R2=0.9309 | VAL lumo_RMSE=0.2257 lumo_MAE=0.1652 lumo_R2=0.9188
・
・
・
[Epoch 043] lr=1.00e-03 train_MSE=0.0403 train_MAE=0.1479 | VAL gap_RMSE=0.1729 gap_MAE=0.1293 gap_R2=0.9510 | VAL homo_RMSE=0.1775 homo_MAE=0.1332 homo_R2=0.9513 | VAL lumo_RMSE=0.1354 lumo_MAE=0.1034 lumo_R2=0.9708
Early stopping triggered (patience=20). Best VAL gap_rmse=0.1529

===== BEST MODEL: VAL (scaled) =====
monitor: gap_rmse = 0.1529

===== FINAL TEST (scaled space) =====
gap {'mae': 0.11299800127744675, 'rmse': 0.15124809741973877, 'r2': 0.9615743160247803}
homo {'mae': 0.12357312440872192, 'rmse': 0.1689915508031845, 'r2': 0.954097330570221}
lumo {'mae': 0.09152957051992416, 'rmse': 0.12056849151849747, 'r2': 0.9760076999664307}

===== FINAL TEST (raw space) =====
gap {'mae': 0.07508999109268188, 'rmse': 0.10050813853740692, 'r2': 0.9615743160247803}
homo {'mae': 0.06590687483549118, 'rmse': 0.09013049304485321, 'r2': 0.954097330570221}
lumo {'mae': 0.0644330158829689, 'rmse': 0.0848752111196518, 'r2': 0.9760076999664307}

[TEST scaled metrics]
                                mae      rmse        r2
target                                                 
gap                        0.112998  0.151248  0.961574
homo                       0.123573  0.168992  0.954097
lumo                       0.091530  0.120568  0.976008
spectral_overlap           0.097456  0.135246  0.972533
homo_extrapolated          0.143133  0.201838  0.939569
lumo_extrapolated          0.126917  0.176347  0.953906
gap_extrapolated           0.161841  0.240020  0.904143
optical_lumo_extrapolated  0.126559  0.170567  0.956577

[TEST raw metrics]
                                  mae        rmse        r2
target                                                     
gap                          0.075090    0.100508  0.961574
homo                         0.065907    0.090130  0.954097
lumo                         0.064433    0.084875  0.976008
spectral_overlap           247.078735  342.885284  0.972533
homo_extrapolated            0.081247    0.114569  0.939569
lumo_extrapolated            0.077861    0.108185  0.953906
gap_extrapolated             0.089421    0.132617  0.904143
optical_lumo_extrapolated    0.074083    0.099843  0.956577

学習ループの流れとして、それぞれのDataLoaderの役割は、

• train : scaled空間でMSEを最小化
• validation : 各エポックで性能を監視
• test : 学習完了後に一度だけ評価 ⇒ データリーク防止

としています。

また、論文ではepochs=500となっていましたが、計算時間節約のため、early_stoppingを使用しています。結構早い段階で学習stopとなりました。

テストデータに対する評価指標を見れば一目瞭然ですが、どの指標においても良い性能を示しているのが分かります。

論文の評価資料と比べてみると、赤枠で囲った部分がMAEの値です。

論文では、gapのMAEが35.4 eVであるのに対して、今回の実装では75.1 eVの約2倍となりました、他の物性値も同程度のずれです。完全に一致とはなりませんでしたが、それでも桁は同じ程度に収まりました。この辺のずれはデータ分割のやり方の違いに起因していると思われます。

以上が、論文に記載された MPNN の学習・評価プロセスをPyTorch Geometricで再現した一連の流れとなります。チャッピーと試行錯誤して完成しました。

まとめ

今回は論文の追試を通して、GNN を用いた分子物性予測を実装しました。以下、GNNが良いなと思った点です。

• 分子グラフは分子構造をそのまま入力として扱えるため、特徴量設計に依存した恣意的な解釈が入りにくい

• GPU を搭載した PC が1台あれば、5万分子規模でも数十分で学習が完了する

• multi-task 学習は、HOMO/LUMO・gap・光学特性など、物理的に関連した複数の物性を同時に学習できる点で、分子グラフ表現と非常に相性が良い

分子を扱う機械学習においてモデル構築を行う際、GNN は強力な選択肢の一つになり得ると実感しました。一度手を動かしてみるとイメージが掴みやすいので、興味のある方はぜひ試してみてください。データセットを変えた時の挙動を見てみるのも面白いと思います。

今回も長文読んでいただき有難うございました。