Rによるディリクレ過程のスクラッチ実装

ノンパラメトリックベイズ

ノンパラメトリックベイズとは、柔軟なモデリングが可能なベイズ統計学の手法の一つです。手法のイメージとしては、パラメトリックな仮定を置かない手法というよりも、通常のベイズ的な手法の複雑さを決定するパラメータを無限大に拡張した手法と言えます。

この記事では、佐藤一誠先生のノンパラメトリックベイズ本を参考に、本の中のモデルを実装していきます。理論的な詳細については、こちらの本をお読み下さい。

ディリクレ過程

ノンパラメトリックベイズ本を参考に、中華料理店過程をもとにした無限混合ガウスモデルを用いたクラスタリングについて簡単に説明します。

ノンパラメトリックベイズだと何が嬉しいのか

基本的なクラスタリング(k-means など)では、分類するクラスの数をあらかじめ設定する必要があります。しかし、クラスの数が未知の場合それを決定することは容易ではないでしょう。ノンパラメトリックベイズを用いることで、クラスの数を決めずとも上手くクラスタリングすることができます。

無限混合ガウスモデル

今回は$n$個の2次元ベクトル$x$$(i = 1,2,...,n)$についてクラスタリングすることを目的とします。また、$i$番目のデータが属するクラスを$z_i$とおくことにします。

混合ガウスモデルの場合、$z_i$が$k$であるとき、データ$x_i$を生成するモデルは平均パラメータ$\mu_k$の正規分布となります。¹　この部分はベイズモデルの尤度として扱われるパーツです。
$$x_i \sim N(\mu_k, \sigma_0^2 I)$$
各クラスの平均パラメータ$\mu_k$の事前分布について、分散既知の正規分布を尤度としたことから、共役事前分布とするために正規分布を仮定します。¹
$$\mu_k \sim N(\mu_0, \sigma_0^2 I)$$
データ$i$が属するクラス$z_i$の事前分布には中華料理店過程²を使用します。

p(z_i = k | z_{- i}) = \left\{
\begin{array}{ll}
\frac{n_k^{-i}}{i-1+\alpha} & (k \in K^+(z_{- i})) \\
\frac{\alpha}{i-1+\alpha}  & (k = |K^+(z_{- i})|+ 1)
\end{array}
\right.

$n_k^{-i}$は$i$以外のクラス$k$に属しているデータの数、$K^+$は登場しているクラスの集合で、$|K^+|$はその数を表しています。ここで、$z_i$の事前分布は自分の属しているクラスについて、$n_k$が１引かれることになります。これにより、属しているデータが１つしかないクラスは一旦消滅することになります。

これらの事前分布を組み合わせることで、モデルの事前分布を作ることができます。少し一般的な形で、データ$x_i$を生成するパラメータを$\theta_i$とおきます。ここでは、$\theta_i$は正規分布の平均パラメータのみを表します。$\mu_k$についての事前分布と$z_i$についての事前分布を組み合わせることで

\theta_i = \left\{
\begin{array}{ll}
\mu_k \ \ (k \in K^+(z_{- i}))\ \ \ \ \  \frac{n_k^{-i}}{i-1+\alpha}の確率で & \\
\mu_{K^+(z_{- i})} \ \ (k = |K^+(z_{- i}|))\ \ \ \ \  \frac{\alpha}{i-1+\alpha}の確率で
\end{array}
\right.

となります。この$\theta_k$の生成とは、データを生成する分布の生成とも捉えられ、これをディリクレ過程と呼びます。

以上の事前分布とこの節で最初に登場した尤度を組み合わせることで$\mu_k$と$z_i$の事後分布が導出できます。$z_i$については中華料理店過程の確率に対して各クラスに属した場合の尤度をかけることで簡単に求まります。

p(z_i = k | z_{- i}) = \left\{
\begin{array}{ll}
\frac{n_k^{-i}}{i-1+\alpha}N(x_i | \mu_k, \sigma_0^2 I) & (k \in K^+(z_{- i}))　\\
\frac{\alpha}{i-1+\alpha}N(x_i | \mu_k, \sigma_0^2 I)  & (k = |K^+(z_{- i})|+ 1)
\end{array}
\right.

$\mu_k$の事後分布の導出についての詳細は割愛させていただきますが、$\mu_k$の事前分布$N(\mu_0, \sigma_0^2 I)$とクラス$k$に属するデータの尤度$\Pi_{i:z_i = k} \ N(x_i | \mu_k, \sigma_0^2 I)$をかけることで導出可能です。

実装

ギブス・サンプラー

今まで説明してきたクラスタリングのモデルをギブス・サンプラーによって推定します。
今回関心があるのは各データがどのようにクラスタリングされるかであるため、ステップごとにで各データどのクラスに割り当てられたかを保存しておきます。最後に保存された$z_i$のサンプルから最頻値をとって推定値とします。

データの準備

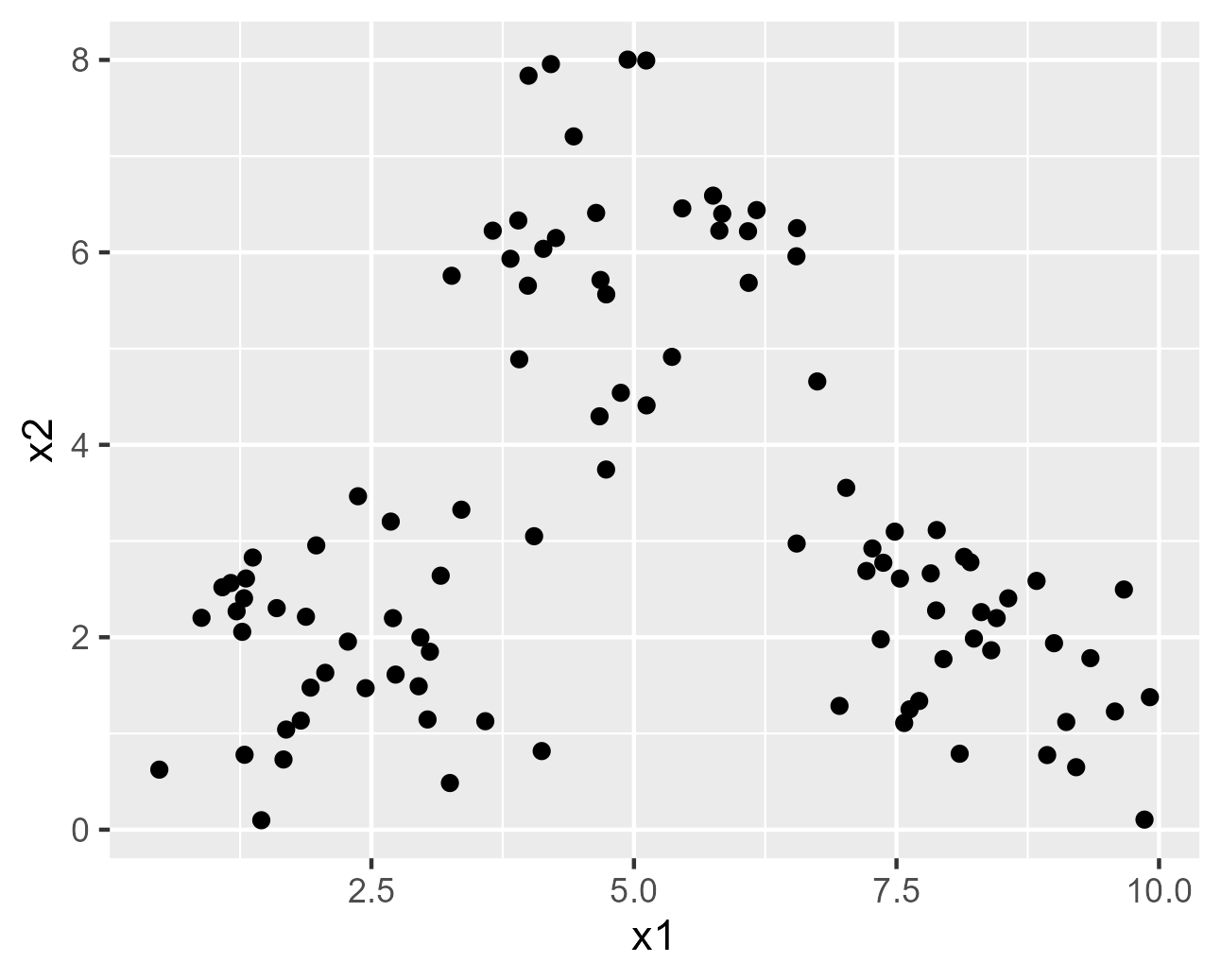
今回は３つの正規分布が組み合わさった、混合正規分布から$n=100$のデータを生成しています。

# data generate
set.seed(428)
n <- 100
mu_1 <- c(2, 2)
mu_2 <- c(5, 6)
mu_3 <- c(8, 2)
sigma <- 1

X <- matrix(nrow = n, ncol = 2)
colnames(X) <- c("x1","x2")
for (i in 1:n){
  z_i <- sample(c(1, 2, 3), size = 1, prob = c(1/3, 1/3, 1/3))
  if(z_i == 1){
    x_i <- mvtnorm::rmvnorm(n = 1, mean = mu_1, sigma = sigma * diag(2))
  }else if(z_i == 2){
    x_i <- mvtnorm::rmvnorm(n = 1, mean = mu_2, sigma = sigma * diag(2))
  }else if(z_i == 3){
    x_i <- mvtnorm::rmvnorm(n = 1, mean = mu_3, sigma = sigma * diag(2))
  }
  
  X[i,] <- x_i
}

生成されたデータのプロットするコードとその出力です。

data_plot <- ggplot2::ggplot(data = X, mapping = ggplot2::aes(x = x1, y = x2)) +
  ggplot2::geom_point()
data_plot

実装

ギブス・サンプリングを行う前に事前分布のパラメータと中華料理店過程の集中度パラメータ$\alpha$を設定します。また、ここでギブス・サンプリングのstep数とburn-inの大きさも決めています。

# params set
alpha <- 1
sigma.0 <- 1
mu.0 <- c(mean(X[,1]), mean(X[,2]))

sample_size <- 1000
burn_in <- 100

$z$について1周目のサンプリングを行います。2周目以降と分けているのは、中華料理店過程の確率の分母の部分が1周目の場合は$i-1+\alpha$で、2周目以降を$n-1+\alpha$とするためです。

# Dir process
mu_list <- list()
num_cluster <- 1

# initial value
z <- c(1, rep(0,n-1))
mu_list[[1]] <- c(X[1,1], X[1,2])
X_and_z <- data.frame("x1" = X[,1],
                      "x2" = X[,2],
                      "z" = z)

# first sample
for (i in 2:n) {
  prob <- rep(0, num_cluster + 1)
  for(k in 1:num_cluster){
    n_k <- sum(z[-i] == k)
    prior_k <- n_k/(n-1+alpha)
    likelyhood_k <- mvtnorm::dmvnorm(X[i,], mean = mu_list[[k]], sigma = sigma.0*diag(2))
    prob_k <- prior_k * likelyhood_k
    prob[k] <-prob_k
  }
  mu_new <- mvtnorm::rmvnorm(n = 1, mean = mu.0, sigma = sigma.0*diag(2))
  likelyhood_new <- mvtnorm::dmvnorm(X[i,], mean = mu_new, sigma = sigma.0*diag(2))
  prior_new <- alpha/(n-1+alpha)
  prob[num_cluster + 1] <- prior_new * likelyhood_new
  
  z_i <- rmultinom(n = 1, size = 1, prob = prob) |> 
    which.max()
  z[i] <- z_i
  
  if(z_i == num_cluster + 1){
    mu_list[[num_cluster + 1]] <- mu_new
    num_cluster <- num_cluster + 1
  }
}

Z <- matrix(nrow = sample_size, ncol = n)

2周目以降のサンプリングについては以下の通りです。
$\mu_k,z_i$の順でサンプリングを行っています。各stepの最後に属しているデータが０になったクラスを消去しています。

# follow sample
for(s in 1:sample_size){
  num_cluster <- max(z)
  
  for (k in 1:num_cluster) {
    n_k <- sum(z == k)
    
    x1_bar_k <- X_and_z |> dplyr::filter(z == k) |> 
      dplyr::summarise(mean(x1))|> as.numeric()
    x2_bar_k <- X_and_z |> dplyr::filter(z == k) |> 
      dplyr::summarise(mean(x2)) |> as.numeric()
    x_bar_k <- c(x1_bar_k, x2_bar_k)
    
    mu_k <- sigma.0/(sigma.0/n_k + sigma.0) * x_bar_k +
      (sigma.0/n_k)/(sigma.0/n + sigma.0)* mu.0
    sigma_k <- 1/(1/sigma.0 + n_k/sigma.0)*diag(2)
    mu_k <- mvtnorm::rmvnorm(n = 1, mean = mu_k, sigma = sigma_k)
    mu_list[[k]] <- mu_k
  }
  
  for (i in 1:n) {
    prob <- rep(0, num_cluster + 1)
    for(k in 1:num_cluster){
      n_k <- sum(z[-i] == k)
      prior_k <- n_k/(n-1+alpha)
      likelyhood_k <- mvtnorm::dmvnorm(X[i,], mean = mu_list[[k]], sigma = sigma.0*diag(2))
      prob_k <- prior_k * likelyhood_k
      prob[k] <-prob_k
    }
    mu_new <- mvtnorm::rmvnorm(n = 1, mean = mu.0, sigma = sigma.0*diag(2))
    likelyhood_new <- mvtnorm::dmvnorm(X[i,], mean = mu_new, sigma = sigma.0*diag(2))
    prior_new <- alpha/(n-1+alpha)
    prob[num_cluster + 1] <- prior_new * likelyhood_new
    prob <- prob |> replace(is.na(prob), 0)
    
    z_i <- rmultinom(n = 1, size = 1, prob = prob) |> 
      which.max()
    z[i] <- z_i
    
    
    
    if(z_i == num_cluster + 1){
      mu_list[[num_cluster + 1]] <- mu_new

    }
  }
  
  X_and_z <- data.frame("x1" = X[,1],
                        "x2" = X[,2],
                        "z" = z)
  
  new_z_df <- X_and_z |>  
    dplyr::group_by(z) |> 
    dplyr::summarise("count" = dplyr::n()) |> 
    dplyr::filter(count > 0)
  new_z_df <- new_z_df |> dplyr::mutate("new_z" = c(1:length(unique(z))))
  
  X_and_z <- X_and_z |> dplyr::left_join(new_z_df, by="z") |> 
    dplyr::mutate("z" = new_z) |> 
    dplyr::select(-c("count","new_z"))
  z <- X_and_z$z
  Z[s,] <- z
  
  mu_list_new <- list()
  for(k in 1:max(z)){
    k_old <- new_z_df |> dplyr::filter(new_z == k) |> 
      dplyr::select(z) |> 
      as.numeric()
    mu_list_new[[k]] <- mu_list[[k_old]]
  }
  mu_list <- mu_list_new
}

for (i in 1:n) {
  z[i] <- modeest::mfv(Z[(burn_in + 1): sample_size,i])
}
X_and_z <- data.frame("x1" = X[,1],
                      "x2" = X[,2],
                      "z" = z)

最後にburn-in部分を捨てて、$z_i$のmodeを取っています。これを今回の各データの推定値とします。

結果のプロット

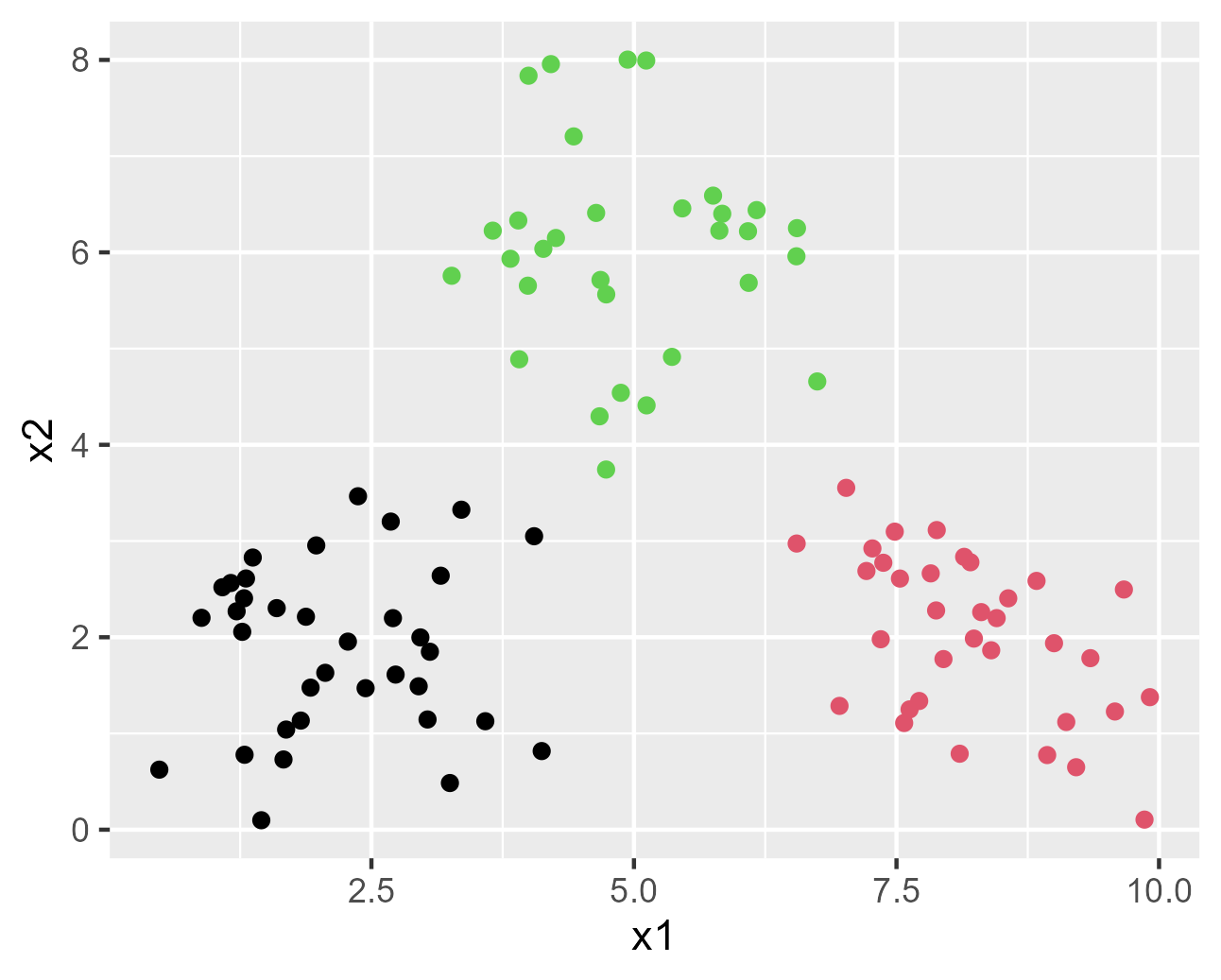
データを3つのクラスに上手く分類できています。

result_plot <- ggplot2::ggplot(data = X_and_z, mapping = ggplot2::aes(x = x1, y = x2)) +
  ggplot2::geom_point(colour = z)
result_plot

参考文献

[1]佐藤一誠. (2016).「ノンパラメトリックベイズ 点過程と統計的機械学習の数理」.　講談社.
(https://www.kspub.co.jp/book/detail/1529151.html)

1. ノンパラメトリックベイズ本を参考にして、正規分布の分散パラメータは各クラス共通して$\sigma_0^2 I$としています。 ↩ ↩²

2. 中華料理店過程についての説明はこちらをお読み下さい。
   Rによる中華料理店過程のスクラッチ実装 ↩