ノンパラメトリックベイズ
ノンパラメトリックベイズとは、柔軟なモデリングが可能なベイズ統計学の手法の一つです。手法のイメージとしては、パラメトリックな仮定を置かない手法というよりも、通常のベイズ的な手法の複雑さを決定するパラメータを無限大に拡張した手法と言えます。
この記事では、佐藤一誠先生のノンパラメトリックベイズ本を参考に、本の中のモデルを実装していきます。理論的な詳細については、こちらの本をお読み下さい。
中華料理店過程
中華料理店過程について簡単に説明します。
中華料理店過程のイメージ
中華料理店に次々とやってくる客は、料理の置いてあるテーブルを一つ選んで座ります。この時、客は自分よりも前に来た客がどのテーブルに集まっているかを見て、人気のあるテーブルに座りたいと考えるでしょう。また稀に、誰も座っていないけど、あのテーブルの料理は美味しそうだと気付き、新しいテーブルに座る客も現れます。このような客が座るテーブルに番号をつけて、それを記述した確率過程が中華料理店過程です。
実装に必要な数式
客、テーブルにはそれぞれ$i = (1,2,...n)$、$k = (1,2,...)$と番号が割り振られてられています。また、$z_i$は客$i$が座ったテーブルの番号を表します。例えば、一人目の客は必ず$k=1$のテーブルに座り($z_1 = 1$)、二人目の客は$k=1$のテーブルか$k=2$($z_2 = 1\ or\ 2$)のテーブルのどちらかに座ります。中華料理店過程において$z_i=k$の確率は以下のようになっています。1
p(z_i = k | z_{1:i-1}) = \left\{
\begin{array}{ll}
\frac{n_k}{i-1+\alpha} & (k \in K^+(1:i-1)) \\
\frac{\alpha}{i-1+\alpha} & (k = |K^+(1:i-1)|+ 1)
\end{array}
\right.
$K^+(1:i-1)$は$1$から$i-1$の客が既に座っているテーブルの集合、$n_k$は各テーブルの人数を表しています。上の式は既に人が座っているテーブル$k$に客が座る確率、下の式は新たなテーブルに座る確率を表しています。
また、パラメータ$\alpha$が登場しています。これは式の形からも分かるように、客が新たなテーブルを選ぶ確率を制御するパラメータであると解釈します。ノンパラメトリックベイズ本を参考にここでは$\alpha=1$として実装しました。
実装
実装
Rのコードは以下の通りです。
# params set
alpha <- 1
n <- 100
z <- c(1)
# CRP process
set.seed(428)
for (i in 2:n) {
num_table <- max(z)
prob <- rep(0, num_table + 1)
for (table in 1:num_table){
num_guest <- sum( z == table)
table_prob <- num_guest/(i - 1 + alpha)
prob[table] <- table_prob
}
prob[num_table + 1] <- alpha/(i - 1 + alpha)
z_i <- rmultinom(n = 1, size = 1, prob = prob) |>
which.max()
z <- c(z, z_i)
}
客の数$n$は100として、最初の客は$k=1$のテーブルに座るものとします。
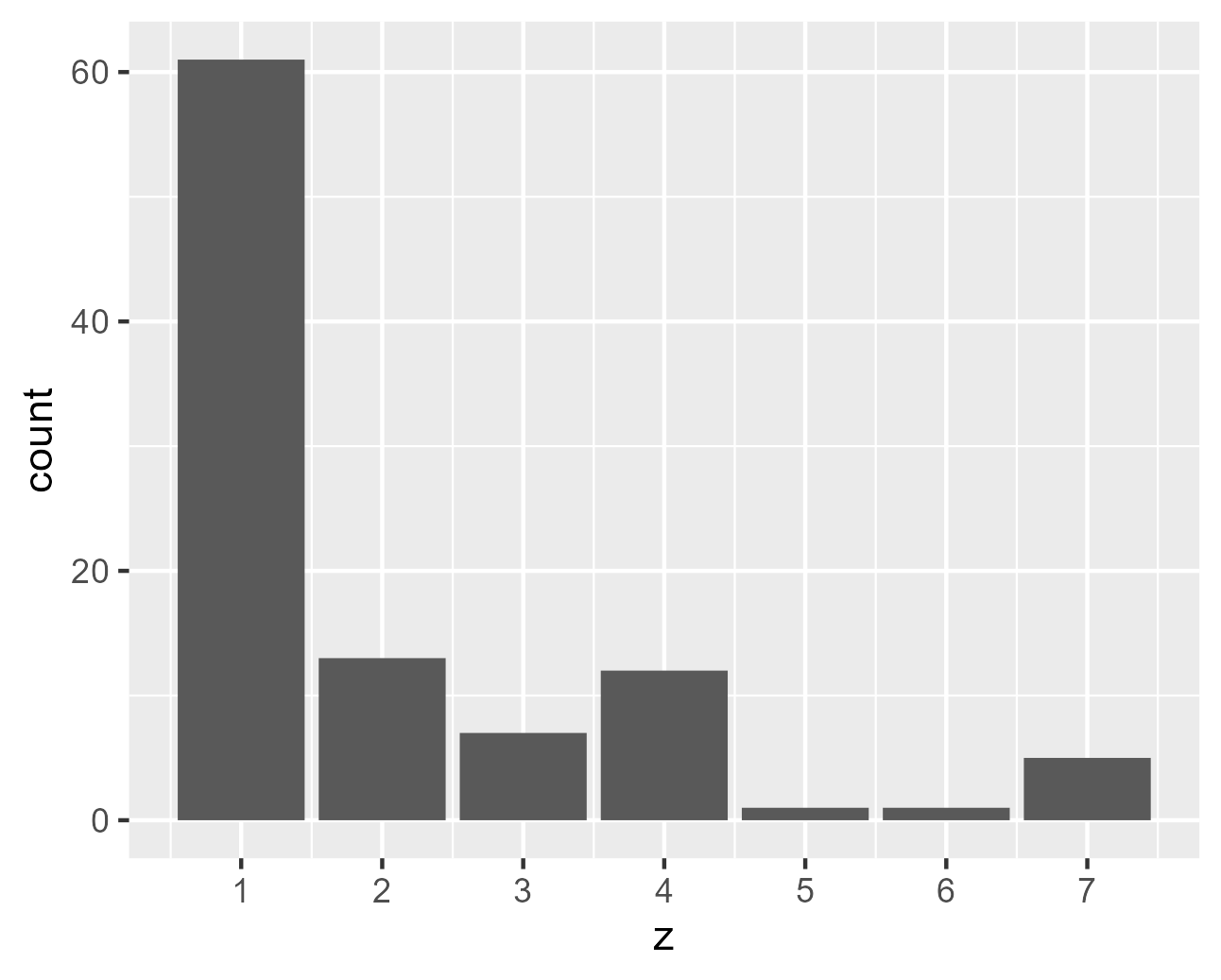
結果のプロット
ggolot2を使ってヒストグラムを表示します。
hist <- ggplot2::ggplot(mapping = ggplot2::aes(x = z)) +
ggplot2::geom_bar() +
ggplot2::scale_x_continuous(breaks = 1:max(z))
hist
テーブル1に客が集中していることが分かります。今回はテーブル4まで生成されました。
付録
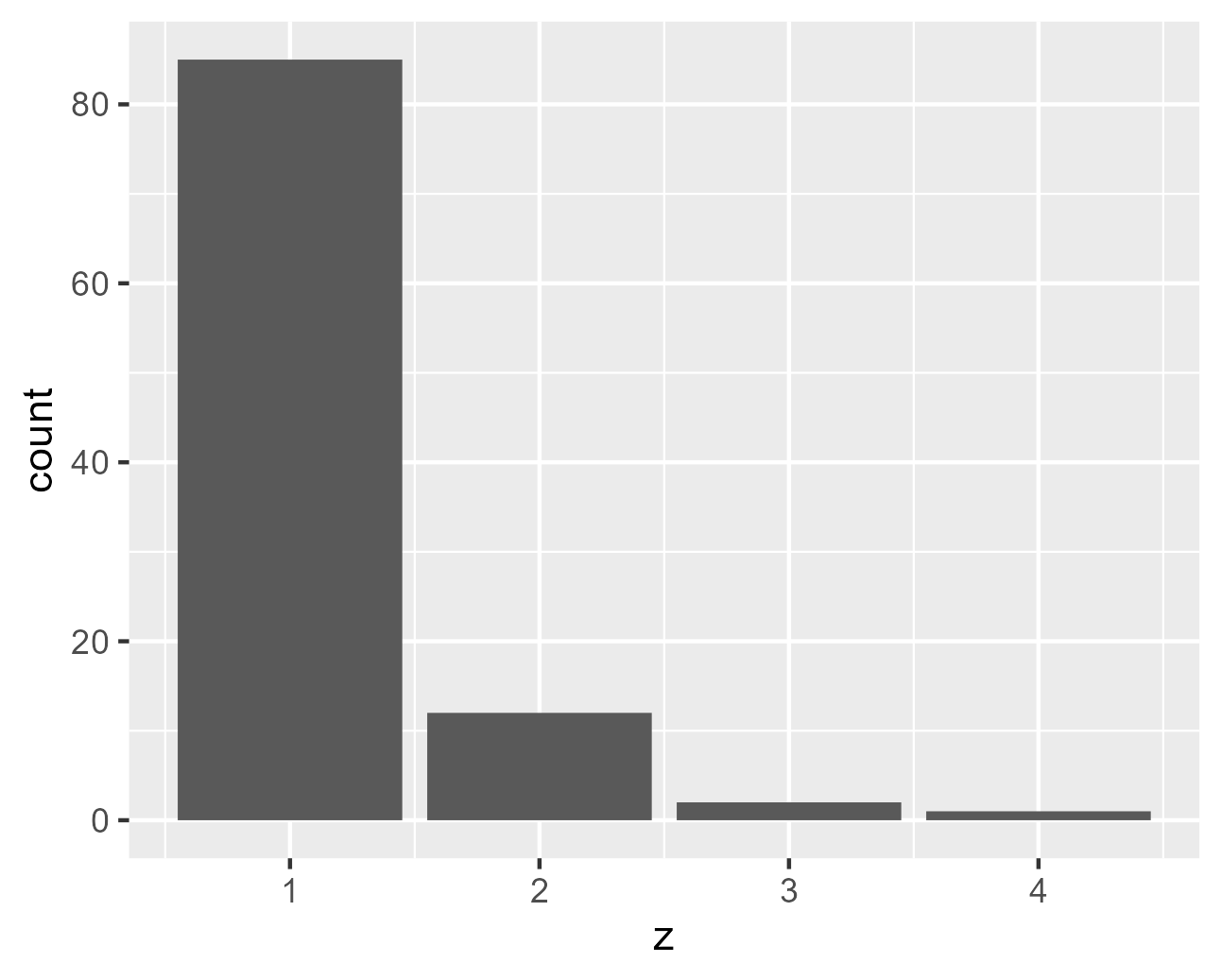
$\alpha$が1のときと比較して、新たなテーブルが選ばれやすくなっています。
参考文献
[1]佐藤一誠. (2016).「ノンパラメトリックベイズ 点過程と統計的機械学習の数理」. 講談社.
(https://www.kspub.co.jp/book/detail/1529151.html)
-
中華料理店過程は、ノンパラメトリックベイズで用いられるディリクレー多項分布モデルとは別に提案されたものですが、後者のモデルにおいてクラスの数を無限にとったときのクラスの分割に関する分布と同じ形になっています。詳しくは、ノンパラメトリックベイズ本をお読み下さい。 ↩