前説
本投稿は勉強メモになります。
(1)とありながら下巻の9章から始めるのですが、これは投稿者(私)の興味と必要になった順にやっていくからです。
前提を書いていきます。
- 和書、丸善版を参考にしています。
- 工業数学の範囲で話すことが多いかと思います。数学的なツッコミは大歓迎ですが、私には理解できないかもしれません。(数学はのちのちやっていきます)
- これを書いている現在は2019年3月になりますが、全部でいくつのシリーズになるか、いつまでに何をやるかは特に定めていません。(1)-1で心が折れたらごめんなさい。
- 理論の理解と演習問題を優先するので、実装をがっつりやる予定はあまりないです。やるとしたらC++で実装します。
0. 第9章の概要
混合モデルとは、混合ガウス分布
p(x) = \sum_{k=1}^{K} \pi_k N(x|{\bf \mu}_k,{\bf \Sigma}_k)
のような、分布の重ね合わせで表されるモデルのことを指します。(混合ガウス分布は、PRML上巻2章の2.3節 P108で出てきます。)
混合モデルを使用するモチベーションとして、例えばクラスタリング問題への適用が挙げられます。上記の混合ガウス分布でクラスタリングを行うと、各クラスタの確率密度分布を求めることが可能となります。
第9章では、EMアルゴリズムと呼ばれる反復法により、混合モデルのパラメータを求めます。
まずは混合ガウス分布のEMアルゴリズムを直感的に説明するために、K-meansによるクラスタリングの話をします。
1. K-meansクラスタリング
K-meansとは
K-meansとは、データがどのクラスタに属するかを推定するクラスタリング手法になります。正確には非階層的クラスタリング手法です。
(脱線しますが、階層的クラスタリング手法とは、データ点の距離を階層的にまとめて二分木のようにクラスタリングしていく手法です。K-meansは"非"階層的です。参考:Toshihiro Kamishima HP)
反復法による解法
データ集合$\bigl\{{\bf x}_1,{\bf x}_2,...,{\bf x}_N\bigr\}$を$K$個のクラスタに分割するとします。k-meansでは、$K$個のクラスタそれぞれの平均ベクトル${\bf \mu}_k(k=1,2,...,K)$を求め、各データを平均ベクトルが一番近いクラスタに割り当てていきます。
まずは、データ点${\bf x}_n$がクラスタ$k$に属する場合に$r_{nk}=1$となり、それ以外では$r_{nk}=0$となる$r_{nk}(n=1,...,N,k=1,...,K)$を導入します。これは**1-of-K符号化法(1-of-K coding scheme)**として知られています。$r_{nk}$の概念はこのあと混合ガウス分布を求める際に重要となるので、よく覚えていてください。
式で見ていきましょう。$r_{nk}$は
r_{nk} = \begin{cases}
1 \quad \text{if} \quad k=\text{arg min}_j||{\bf x}_n-{\bf \mu}_j||^2\\
0 \quad \text{else}
\end{cases}\tag{1}
となります。
K-meansでは、
J = \sum_{n=1}^{N}\sum_{k=1}^{K}r_{nk}||{\bf x}_n-{\bf \mu}_j||^2\tag{2}
を最小にする$r_{nk}$と${\bf \mu}_k$を求めます。$||…||$はベクトルのノルムです。この目的関数$J$は**歪み尺度(distortion measure)**と呼ばれることもあります。(なぜでしょう?教えてください。)
求めていきましょう。
$r_{nk}$は先ほどの式(1)を満たすもので、$\mu_k$が決まればすぐに解けます。
$\mu_k$は、式(2)で$r_{nk}$を固定したときの最小化問題
{\bf \mu}_k = \text{arg min}_{\bf u}\sum_{n=1}^{N}r_{nk}||{\bf x}_n-{\bf u}||^2\tag{3}
を解いて求めていきます。まず、式(3)の関数を${\bf u}$に関して偏微分し、以下の式を得ます。
\frac{∂}{∂ {\bf u}}\sum_{n=1}^{N}r_{nk}||{\bf x}_n-{\bf u}||^2
= 2\sum_{n=1}^{N}r_{nk}({\bf x}_n-{\bf u})\tag{4}
式(4)が$0$になる${\bf u}$を求めることで、式(3)の解が求まります。
\begin{equation}
2\sum_{n=1}^{N}r_{nk}({\bf x}_n-{\bf u}) = 0
\end{equation}
\begin{equation}
\sum_{n=1}^{N}r_{nk}{\bf u} =\sum_{n=1}^{N}r_{nk}{\bf x}_n
\end{equation}
\begin{equation}
{\bf u}={\bf \mu}_k=\frac{\sum_{n=1}^{N}r_{nk}{\bf x}_n}{\sum_{n=1}^{N}r_{nk}}\tag{5}
\end{equation}
$r_{nk}(n=1,...,N)$は離散的な変数であるため有限であり、${\bf \mu}_k$は$r_{nk}$に対して一意に求まるため、この最小化問題は発散することはなく必ず収束します。
一応、図も載せておきましょう。反復することで、下図の(i)の状態に収束します。
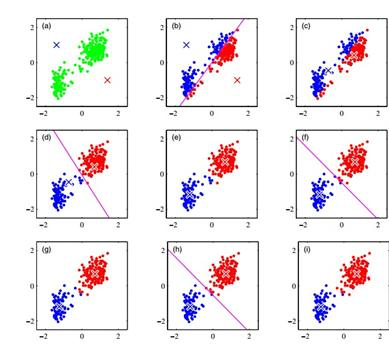
出典:https://blog.csdn.net/Nietzsche2015/article/details/43450851
Robbins-Monro法による逐次推定について
PRML本書では、この後Robbins-Monro法による逐次推定と、目的関数$J$の二乗ユークリッド距離を非類似度$V({\bf x}_k,{\bf \mu}_k)$で代替する**K-medoidosアルゴリズム(K-medoids algorithm)**の紹介、画像分割や画像圧縮への応用の話が続きます。ここではRobbins-Monro法の話だけします。
Robbins-Monro法は、PRML2章の2.3.5節でガウス分布のパラメータの最尤推定を行うために出てきます。逐次推定は、大規模データ集合を扱う場合にとても有効です。が、K-meansへの適用の場合、この利点は小さいかもしれません。(K-meansは計算量が$O(KN)$なので、データ数$N$が膨大になっても計算コストが飛躍的に大きくはなりにくい、${\bf \mu}_k$を求めた後にデータ点の割り当てを行う必要がある、等々・・・。)
まずは一般的なRobbins-Monro法についてざっくり紹介します。
2つの相関がある確率変数$z$と$\theta$について、条件付き期待値${\bf E}[z|\theta]$で与えられる回帰関数$f(\theta)$を以下のように定義します。
f(\theta)\equiv{\bf E}[z|\theta]=\int zp(z|\theta)\text{d}z\tag{6}
$p(…)$は適当な確率密度関数としておきましょう。連続的な$z$と、$z$に関する$\theta$の条件付き確率密度関数$p(z|\theta)$を掛けて、積分し、$z$の条件付き期待値を算出しています。
ここでの目標は、回帰関数$f(\theta^{*})=0$となる根$\theta^{*}$を求めることです。Robbins-Monro法では、回帰関数の根$\theta^{*}$の推定を以下のように行います。
\theta^{(n)}=\theta^{(n-1)}-a_{n-1}z(\theta^{(n-1)})\tag{7}
$z(\theta^{(n-1)})$は、$\theta$が$\theta^{(n-1)}$を取るときに観測される$z$を意味します。
$a_n$は、以下の条件を満たす正数の系列になります。
\lim_{n \to \infty}a_n=0\\
\sum_{n=1}^{\infty}a_n=\infty\\
\sum_{n=1}^{\infty}a^2_n<\infty
これは、①式(7)が極限値に収束する ②アルゴリズムが根以外に急速に収束をしない ③蓄積されたノイズの分散を有限に抑え、収束を阻害しない の3点を保証するために必要な条件になります。$n$が小さいうちは$a_n$が大きく、$n$が$\infty$に近づくほど$0$に漸近し、かつ二乗和が有限になるものですね。
これをK-meansの${\bf \mu}_k$に対して適用します。
今回の目標は、目的関数$J$の${\bf \mu}_k$に関する偏微分
g({\bf x},{\bf \mu}_k)=\frac{∂}{∂ {\bf \mu}_k}\sum_{n=1}^{N}r_{nk}||{\bf x}_n-{\bf \mu}_k||^2
= 2\sum_{n=1}^{N}r_{nk}({\bf x}_n-{\bf \mu}_k)\tag{8}
が$0$となる根${\bf \mu}_k^{*}$を求めることです。式(8)=式(4)です。これを$g({\bf x},{\bf \mu}_k)$と置きましょう。
上記の$z(\theta^{(n-1)})$は、$g({\bf x}_n,{\bf \mu}_k^{n-1})$と表すことができます。これは、$r_{nk}=1$の場合、
g({\bf x}_n,{\bf \mu}_k^{n-1})=2({\bf x}_n-{\bf \mu}_k^{n-1})\tag{9}
となります。よって、K-meansにRobbins-Monro法を適用させると、
{\bf \mu}_k^{new}={\bf \mu}_k^{old}+\eta_n({\bf x}_n-{\bf \mu}_k^{old})\tag{10}
と書くことができます。ただし、$\eta_n$は負数の系列です。$\eta_n$にしたのはPRMLに準じているだけです。
この更新は$r_{nk}=1$の時のみ行います。$new$と$old$という書き方をしたのはこれが理由で、必ずしも全てのデータ$N$に対して更新しないからです。(式(9)では、説明のため便宜上${\bf \mu}_k^{n-1}$と書きました。)
2. 混合ガウス分布
混合ガウス分布によるクラスタリング問題の再考
K-meansによるクラスタリングは、データ点がいずれかのクラスタ$k$に必ず属する、いわゆるハードな割り当てでした。また、K-meansはデータ点と各クラスタの平均点のノルムの二乗を評価するため、各クラスタの特性(形状とでも言いましょうか)を無視したクラスタリングになってしまうことがあります。
そこで、混合ガウス分布
p({\bf x}) = \sum_{k=1}^{K} \pi_k N({\bf x}|{\bf \mu}_k,{\bf \Sigma}_k)\tag{11}
を導入してみます。これにより、以下のようなメリットが生じます。
- データ点がどの各クラスタへ属するか、確率として算出することができる。 → ハードな割り当てでなくなり、曖昧さを考慮することができる。
- 分散${\bf \Sigma}_k$の導入により、各クラスタの特性を考慮することができる。
K-meansを基とした反復法による解法
K-meansでは、$r_{nk}$を導入して1-of-K符号化法を取りました。今回は2値確率変数$z_k(k=1,...,K)$を導入します。$z_k$は下記の条件を満たす変数です。
z_k \in \bigl\{ 0,1 \bigr\}\\
\sum_{k=1}^K z_k = 1
$z_k=1$のとき、すべてのデータ点がクラスタ$k$に属します。この確率を
p(z_k=1) = \pi_k\tag{12}
としましょう。$\pi_k$は確率なので、
0\leq \pi_k \leq 1\\
\sum_{k=1}^K \pi_k = 1
を満たします。
$z_k$を要素とする$K$次元ベクトル${\bf z}$の分布は、
p({\bf z})=\prod_{k=1}^{K}\pi_k^{z_k}\tag{13}
と表せます。
さて、我々が最終的に求めたい値は$p({\bf x})$でした。これは
p({\bf x}) = \sum_{\bf z}p({\bf z})p({\bf x}|{\bf z})\tag{14}
と書けます。$p({\bf z})$は周辺分布で、$p({\bf x}|{\bf z})$は${\bf x}$の${\bf z}$に対する条件付き確率です。
周辺分布$p({\bf z})$は先ほど求めました。では条件付き確率$p({\bf x}|{\bf z})$を考えます。これは、
p({\bf x}|{\bf z}) = \prod_{k=1}^{K}N({\bf x}|{\bf \mu}_k,{\bf \Sigma}_k)^{z_k}\tag{15}
となります。式(13)、式(15)を式(14)に代入すると、確かに式(11)になります。
データ集合${\bf X}=\bigl\{{\bf x}_1,{\bf x}_2,...,{\bf x}_N\bigr\}$に混合ガウス分布をあてはめる問題を考えます。それぞれの${\bf x}_n$に対応する潜在変数${\bf z}_n$の集合を${\bf Z}=\bigl\{{\bf z}_1,...,{\bf z}_N\bigr\}$としておきましょう。${\bf z}_n$の性質を考えると、${\bf Z}$の各要素$z_{nk}$はK-meansの$r_{nk}$と同じ性質になります。
${\bf X}$の条件付き確率
p({\bf X}|{\bf \pi},{\bf \mu},{\bf \Sigma})=\prod_{n=1}^N \sum_{k=1}^K \pi_k N({\bf x}_n|{\bf \mu}_k,{\bf \Sigma}_k)\tag{16}
について考えていきます。式(16)の対数尤度関数は、
\text{ln }p({\bf X}|{\bf \pi},{\bf \mu},{\bf \Sigma})=\sum_{n=1}^N \text{ln } \Bigl\{\sum_{k=1}^K \pi_k N({\bf x}_n|{\bf \mu}_k,{\bf \Sigma}_k)\Bigr\}\tag{17}
と表すことができます。
この後、各パラメータで偏微分して最尤推定を行おうとするのですが、混合ガウス分布は特異点(とあるデータ点${\bf x}_n$と平均点${\bf \mu}_k$が一致し、かつ分散が$0$に漸近する場合、対数尤度関数が$\infty$に発散する)が存在し、また尤度関数の微分を$0$と置いても陽な解を得ることができません。そこで、EMアルゴリズムを用いて、性質の良い局所解を求めていきます。
式(17)を${\bf \mu}_k$で偏微分します。
\begin{align}
\frac{∂}{∂ {\bf \mu}_k}\text{ln }p({\bf X}|{\bf \pi},{\bf \mu},{\bf \Sigma})=\frac{∂}{∂ {\bf \mu}_k}\sum_{n=1}^N \text{ln } \Bigl\{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j)\Bigr\}\\
=\sum_{n=1}^N \frac{∂}{∂ {\bf \mu}_k} \text{ln } \Bigl\{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j)\Bigr\}\\
=\sum_{n=1}^N \frac{1}{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j)}\cdot
\frac{∂}{∂ {\bf \mu}_k} \sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j) \\
=\sum_{n=1}^N \frac{1}{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j)}\cdot\pi_k N({\bf x}_n|{\bf \mu}_k,{\bf \Sigma}_k) \cdot {\bf \Sigma}_k^{-1}({\bf x}_n-{\bf \mu}_k)\end{align}
整理して、これが$0$となるような${\bf \mu}_k$を求めると、
\begin{equation}
\sum_{n=1}^N \frac{\pi_k N({\bf x}_n|{\bf \mu}_k,{\bf \Sigma}_k)}{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j)} {\bf \Sigma}_k^{-1}({\bf x}_n-{\bf \mu}_k)=0
\end{equation}
\begin{equation}
\sum_{n=1}^N \frac{\pi_k N({\bf x}_n|{\bf \mu}_k,{\bf \Sigma}_k)}{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j)}{\bf \mu}_k = \sum_{n=1}^N \frac{\pi_k N({\bf x}_n|{\bf \mu}_k,{\bf \Sigma}_k)}{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j)}{\bf x}_n
\end{equation}
{\bf \mu}_k = \frac{1}{\sum_{n=1}^N \frac{\pi_k N({\bf x}_n|{\bf \mu}_k,{\bf \Sigma}_k)}{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j)}}\sum_{n=1}^N \frac{\pi_k N({\bf x}_n|{\bf \mu}_k,{\bf \Sigma}_k)}{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j)}{\bf x}_n\tag{18}
長いのでまとめたいです。そこで、
\gamma(z_{nk})=\frac{\pi_k N({\bf x}_n|{\bf \mu}_k,{\bf \Sigma}_k)}{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j)}\tag{19}
と置いてみます。この$\gamma(z_{nk})$、$p(z_k=1|{\bf x}_n)$と同値になります。というのも、式(12)、式(15)より、
p(z_k=1) = \pi_k
p({\bf x}_n|z_k=1) = N({\bf x}_n|{\bf \mu}_k,{\bf \Sigma}_k)
となるため、式(19)は
\frac{\pi_k N({\bf x}_n|{\bf \mu}_k,{\bf \Sigma}_k)}{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j)}
=\frac{p(z_k=1)p({\bf x}_n|z_k=1)}{\sum_{j=1}^Kp(z_k=1)p({\bf x}_n|z_k=1)}=p(z_k=1|{\bf x}_n)
\tag{20}
と書くことができます。つまり、$\gamma(z_{nk})$は${\bf x}_n$を観測したときの$z_{k}$の事後確率となります。
少し拡張して考えると、式(20)はデータ集合$\bigl\{{\bf x}_1,{\bf x}_2,...,{\bf x}_N\bigr\}$の各データ点に対する1-of-K符号化法の変数$z_{nk}$が$1$となる確率、と考えることができます。$z_{nk}$はK-meansでいう$r_{nk}$と同じなので、データ点${\bf x}_n$が要素$k$に属すれば$1$、そうでない場合は$0$になります。式(20)は1-of-K符号化法の変数もとい潜在変数${\bf z}_k$の事後確率を求めていると言えます。
また、$\gamma(z_{nk})$は要素$k$が${\bf x}_n$の観測を説明する度合い、と表現することもできます。そこで、$\gamma(z_{nk})$を**負担率(responsibility)**と表現します。
さて、$\gamma(z_{nk})$を用いて式(18)を表現していきましょう。より簡単に表すために、以下の$N_k$を導入します。
N_k=\sum_{n=1}^N\gamma(z_{nk})\tag{21}
$N_k$は要素$k$に割り当てられるデータ点の「実効的」な数、と解釈できます。$N_k$と$\gamma(z_{nk})$により、式(18)は
{\bf \mu}_k = \frac{1}{N_k}\sum_{n=1}^{N}\gamma(z_{nk}){\bf x}_n \tag{22}
と表すことができます。すっきりしました、よかったですね。
式(22)の${\bf \mu}_k$は、データ集合の各点${\bf x}_n$の重み付き平均となっています。データ点${\bf x}_n$の重み因子は負担率$\gamma(z_{nk})$で、これは要素$k$がデータ点${\bf x}_n$の生成にどれくらい寄与(負担)しているか、を表していると解釈することもできます。
${\bf \Sigma}_k$も求めていきましょう。式(17)を${\bf \Sigma}_k$で微分します。
\begin{align}
\frac{∂}{∂ {\bf \Sigma}_k}\text{ln }p({\bf X}|{\bf \pi},{\bf \mu},{\bf \Sigma})=\frac{∂}{∂ {\bf \Sigma}_k}\sum_{n=1}^N \text{ln } \Bigl\{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j)\Bigr\}\\
=\sum_{n=1}^N \frac{∂}{∂ {\bf \Sigma}_k} \text{ln } \Bigl\{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j)\Bigr\}\\
=\sum_{n=1}^N \frac{1}{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j)}\cdot
\frac{∂}{∂ {\bf \Sigma}_k} \sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j) \\
=\sum_{n=1}^N \frac{1}{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j)}\Bigl\{ -\frac{1}{2} \cdot \frac{1}{|{\bf \Sigma}_k|} \cdot N({\bf x}_n|{\bf \mu}_k,{\bf \Sigma}_k) + \frac{1}{2} \cdot \frac{1}{|{\bf \Sigma}_k|^2} \cdot ({\bf x}_n-{\bf \mu}_k) ({\bf x}_n-{\bf \mu}_k)^\text{T} \cdot N({\bf x}_n|{\bf \mu}_k,{\bf \Sigma}_k) \Bigr\} \end{align}
これが$0$となる${\bf \Sigma}_k$は、
{\bf \Sigma}_k = \frac{1}{N_k}\sum_{n=1}^{N}\gamma(z_{nk})({\bf x}_n-{\bf \mu}_k)({\bf x}_n-{\bf \mu}_k)^\text{T} \tag{23}
となります。
最後は$\pi_k$ですが、$\pi_k$は総和が$1$であるという制約条件がありました。ラグランジュの未定乗数法の出番です。$\lambda$を導入し、
\text{ln }p({\bf X}|{\bf \pi},{\bf \mu},{\bf \Sigma}) + \lambda \Bigl( \sum_{k=1}^K \pi_k - 1 \Bigr)
=\sum_{n=1}^N \text{ln } \Bigl\{\sum_{k=1}^K \pi_j N(x_n|{\bf \mu}_k,{\bf \Sigma}_k)\Bigr\}+ \lambda \Bigl( \sum_{k=1}^K \pi_k - 1 \Bigr)\tag{24}
を考えます。式(24)を$\pi_k$で偏微分すると、
\frac{∂}{∂ \pi_k}\biggl\{\sum_{n=1}^N \text{ln } \Bigl\{\sum_{j=1}^K \pi_j N(x_n|{\bf \mu}_j,{\bf \Sigma}_j)\Bigr\}+ \lambda \Bigl( \sum_{j=1}^K \pi_j - 1 \Bigr)\biggr\}
=\sum_{n=1}^N \frac{1}{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j)}N({\bf x}_n|{\bf \mu}_k,{\bf \Sigma}_k)+\lambda
\tag{25}
となります。式(25)が$0$となる$\lambda$、$\pi_k$を考えてみましょう。
式(25)の前半部分は$N_k$の式に似ていますが、$\pi_k$が足りません。そこで$\pi_k$を掛けてみましょう。
\sum_{n=1}^N \frac{\pi_k N({\bf x}_n|{\bf \mu}_k,{\bf \Sigma}_k)}{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j)}+\lambda \pi_k =0
\tag{26}
$\pi_k$は$\sum_{k=1}^K \pi_k = 1$を満たします。式(26)をkについて和を取ってみます。
\sum_{k=1}^K \sum_{n=1}^N \frac{\pi_k N({\bf x}_n|{\bf \mu}_k,{\bf \Sigma}_k)}{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j)}+\lambda \sum_{k=1}^K \pi_k =0
\tag{27}
式(27)の前半部分、$k$について和を取ると$N$になります。全てのデータ点に対する要素の負担率の和は、データ点の数と等しくなるのです。
これより、
\lambda = -N
\tag{28}
を導出できました。さて、式(28)の$\lambda$を式(26)に代入すると、
\pi_k = \frac{N_k}{N}
\tag{29}
となります。つまり、要素$k$の混合係数$\pi_k$は、全データ点に対する要素$k$の負担率の平均、で与えられます。
これで、$\gamma(z_{nk})$で混合ガウス分布のパラメータ${\bf \mu}_k$、${\bf \Sigma}_k$、$\pi_k$を表すことができました。(PRMLでは「陽な解ではない」ことを強調しています。なぜでしょう?次の変分推定法に繋がるのかな?)$\gamma(z_{nk})$を求めた後、各パラメータの値を算出することを反復する推定法が、混合ガウス分布という特殊な混合モデルにおけるEMアルゴリズムです。
まとめます。
-
${\bf \mu}_k$、${\bf \Sigma}_k$、$\pi_k$に適当な初期値を代入する(PRMLでは、K-meansで前もって求めておくとよい、と書いてあります。これは前述した特異点への収束を防ぐためです。)
-
$\gamma(z_{nk})$を求める:E(Expectation)ステップ
\gamma(z_{nk})=\frac{\pi_k N({\bf x}_n|{\bf \mu}_k,{\bf \Sigma}_k)}{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j,{\bf \Sigma}_j)} -
${\bf \mu}_k$、${\bf \Sigma}_k$、$\pi_k$を求める:M(Maximization)ステップ
{\bf \mu}_k = \frac{1}{N_k}\sum_{n=1}^{N}\gamma(z_{nk}){\bf x}_n \\ {\bf \Sigma}_k = \frac{1}{N_k}\sum_{n=1}^{N}\gamma(z_{nk})({\bf x}_n-{\bf \mu}_k)({\bf x}_n-{\bf \mu}_k)^\text{T} \\ \pi_k = \frac{N_k}{N} -
対数尤度$\text{ln }p({\bf X}|{\bf \pi},{\bf \mu},{\bf \Sigma})$を計算し、収束基準を満たしていなければ2に戻る
今後の予定
一般のEMアルゴリズムについて話し、もう一度混合ガウス分布について解いた後、ベイズ回帰に対するEMアルゴリズムを見ていきます。
(ここから先が全然進まないので、一区切り入れました。なるべく近いうちに(1)-2を書きます。書きたい・・・。)