この記事は「【マイスター・ギルド】本物の Advent Calendar 2020」14日目の記事です。
ご挨拶
こんにちは。
マイスター・ギルド(MG) 開発部の野澤です。
本記事では、タイトルにあるように数値シミュレーションについて書いています。
具体的には全微分方程式の数値解法(数値シミュレーション)についてです。
Git(ギット)と数値シミュレーションの根っこの考え方って似てるので、Gitを使えるなら数値シミュレーションも理解できるんです。
Gitを使える皆さん、数値シミュレーションもできるんやで?
※ ちなみにMGのメンバーは私含め「きゃっきゃっ」「とぅんくとぅんく」しており、楽しい雰囲気でお仕事しています。
MGへの就職・転職をお考えの皆様、普段は数学とか物理の話なんて全くしませんのでご安心ください!
Gitについておさらい
IT系のエンジニアの方なら日常から利用されているGit。
便利ですよねぇ。
複数人での共同開発が円滑に進みますよね。
WikiにはGitについて「プログラムのソースコードなどの変更履歴を記録・追跡するための分散型バージョン管理システム」と書かれています。
git initで新規のリポジトリを作成し、
ソースコードを変更したあとはgit commitを実行することで変更履歴を記録していきます。
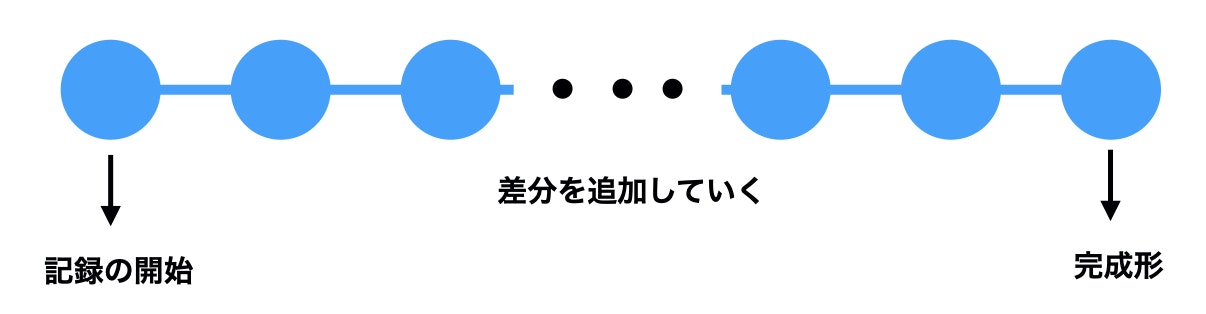
Gitを使えば変更(差分)を記録できます。
この差分を積み重ねていくことで、最初の状態から目的の状態(完成形)へ成長させる。
"差分の積み重ねによって、目的のものを作り出す"
実はこの工程、微分方程式の数値解法と全く同じなんです。
微分方程式の数値解法(数値シミュレーション)
そもそも微分方程式って何?
微分方程式というのはざっくりいうと現象を表す式です。
例えば以下のような微分方程式の場合は、
左辺が勾配(変化の割合)を表し、右辺は2という数値です。
つまり、「yはxが1変化すると2変わる」ということを表します。
\begin{aligned}
\frac{dy}{dx} = 2
\end{aligned}
yとかxに苦手意識がある方に知っておいてもらいたいことは、yとxという文字にはなんの意味もないということです。
それぞれに意味を持たせて、y → N(数:NumberのN)でも、x → t(時間[s]:timeのt)でもいいんです。
\frac{dN}{dt} = 2
こう書くと、「1秒時間が経つとNという数は2増える」という、意味のある式に見えてきません?
次の式とかはどうでしょう?
\frac{dP}{dt} = mP
この式は経済学者マルサスの
「人口の増加率(dP/dt)が人口(P)そのものに比例(m倍)する」
というマルサスモデルという生体の個体数変化のモデルを式にしたものです。
微分方程式についてはなんとなくわかってもらえたかと思うんですが、このままだとあんまり役に立ちません。
上に書いたように微分方程式を"解く"ことで、生体の個体数がどう変化するのかが具体的にわかる(数値シミュレーションできる)ので役に立ちます。
「微分方程式を自分でつくる → その式を解く」という一連の流れができるようになると楽しいですよ!
(ほとんどの人は誰かが作ってくれた式を解いてるだけ。自分も含めてですが。。。)
微分方程式を"解く"ってどういうこと?
微分方程式を解いたことがなくても、単なる方程式なら解いたことがあると思います。
x^2 - 3x + 2 = 0
この式を満たすxは
x = 1, 2
ですね。
単なる方程式の場合は、式を満たす"数"が未知であり、
未知な数を求めることを"解く"と表現していました。
微分方程式の場合は、式を満たす"関数"が未知であり、
未知な関数を求めることを"解く"と表現します。
どういうことかというと、
\frac{dN}{dt} = 2
この場合は、未知な関数Nを求めることを、"解く"といいます。
これは簡単で、両辺をtで積分して、
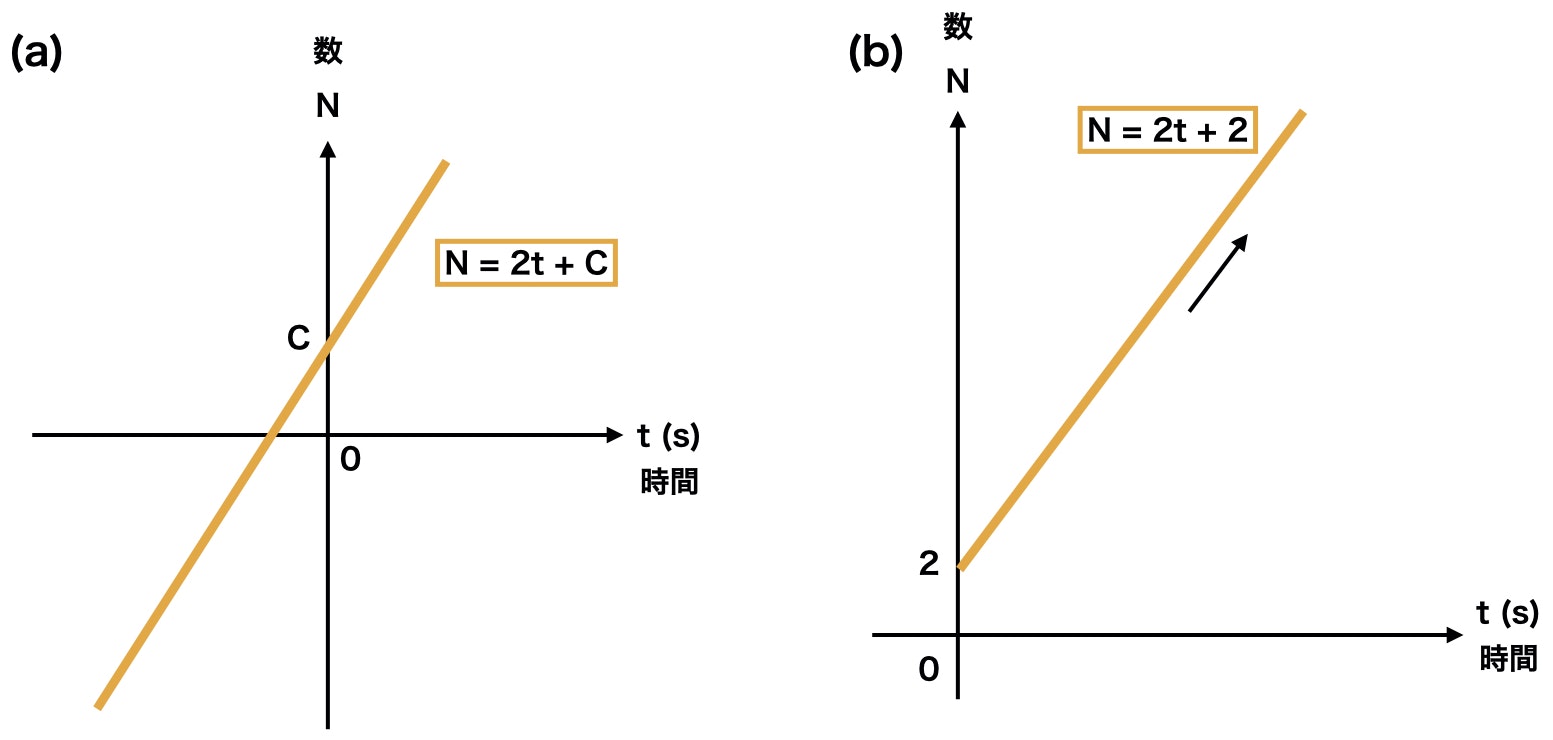
N(t) = 2t + C \ \ \ (Cは積分定数)
となり、グラフにすると下図(a)のようになります。
もしこの式に
N(0)=2, \ \ t \geqq 0
というような条件(初期条件といいます。)があればCは簡単に求まり、下図(b)のようになります。
時間に比例して数が増えていくのがわかりますね!!!
微分方程式の解き方には2種類ある
微分方程式を解き方には以下の2種類があります。
1. 解析的に解く方法
2. 数値的に解く方法
1の解析的に解く方法は上でお見せしたような積分を用いた方法です。
この方法はものすごく正確な解を(厳密解)を求めることができますが、
この方法で解ける微分方程式には限りがあります。(残念すぎる)
理系の大学1年生はこの解析的な解き方をとにかく訳もわからず覚えさせられるですよねぇ。。。(遠い目)
一方、
2の数値的に解く方法を使うと、とてつもなく多くの種類の微分方程式を解けるんです!!(これを伝えたかった)
ですが、精度は上の方法には劣ります。(いわゆる近似解というものを求めることになります。)
長々と書いてきましたが、この数値的な解法がGitと同じ考え方なんです!!!
正直大学1年生のときにこっちの解き方を授業で教わりたかった。(ぼやき)
数値的な解法の説明
さっきから何度も出てる次の式を使って数値的に解いてみましょう。
\frac{dN}{dt} = 2
数値的に解く時は、微分方程式を差分方程式に変換します。
\begin{aligned}
\frac{\Delta N}{\Delta t} &= 2\\
初期条件: N(0) &= 2
\end{aligned}
これが差分方程式です。dをΔ(デルタ)に変えただけですね。
Δっていうのは変化の幅とか差分を意味します。
この式を少し変形すると
\Delta N = 2\Delta t
となり、この式は「Nの変化(ΔN)は時間変化(Δt)の2倍」という意味になります。
これを式のまま素直に受け取ると「ΔN は 2Δt」となります。
つまりですよ? 差分がわかってることになるなんです。
Gitで例えると、"常に2Δtをコミットしまくるって感じ"です。
時間変化(Δt)が1秒なら2(=2x1)の差分をコミット
時間変化(Δt)が2秒なら4(=2x2)の差分をコミット
時間変化(Δt)が2.5秒なら5(=2x2.5)の差分をコミット
...
という感じです。
最初のコミット(初期条件)は2なので、
つまり、2 に 2Δtをずっと足していけば解は求まります!!
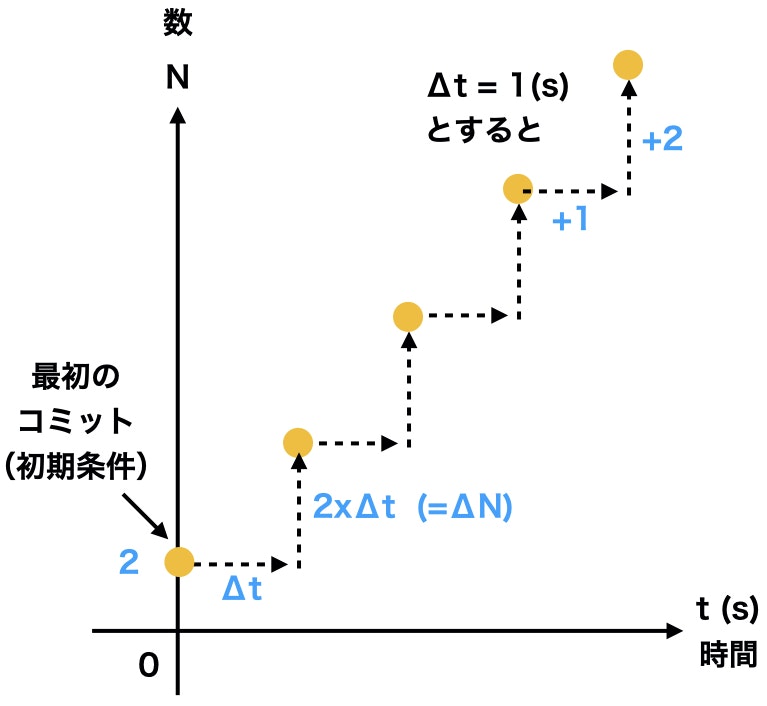
言葉だけで説明してもよくわからないと思うので図で説明しますと、、
Δtを小さく設定すれば、点と点の距離は短くなり、点の軌跡は直線のようになります。
その直線というのが、上で解析的に解いたときの
N(t) = 2 t + 2 \ \ \ (t \geqq 0)
です。
これが微分方程式の数値的な解法というもので、数値シミュレーションってやつです。
単なる足し算なんですよ。簡単でしょ?
Pythonを使ってこの計算をやってみると以下のようになります。
import matplotlib.pyplot as plt
import numpy as np
def difference(delta):
return 2*delta
# 配列の準備
totlaNum = 50 # とりあえず50にしているだけ
time = np.zeros(totlaNum, dtype = float)
number = np.zeros(totlaNum, dtype = float)
# 初期値
time[0] = 0.0
number[0] = 2.0
deltaTime = 0.1 #←もっと細かくしても良い
# 計算
for i in range(totlaNum-1):
# 差分を足してるだけなんです。Gitであれば差分のコミットにあたるのがここです。
number[i+1] = number[i] + difference(deltaTime)
time[i+1] = time[i] + deltaTime
# plot
plt.plot(time, number, 'r-', lw = 2, color='red')
plt.xlabel('t (s)', fontsize=15)
plt.ylabel('N', fontsize=15)
plt.savefig('line.png', dpi=600)
# show
plt.show()
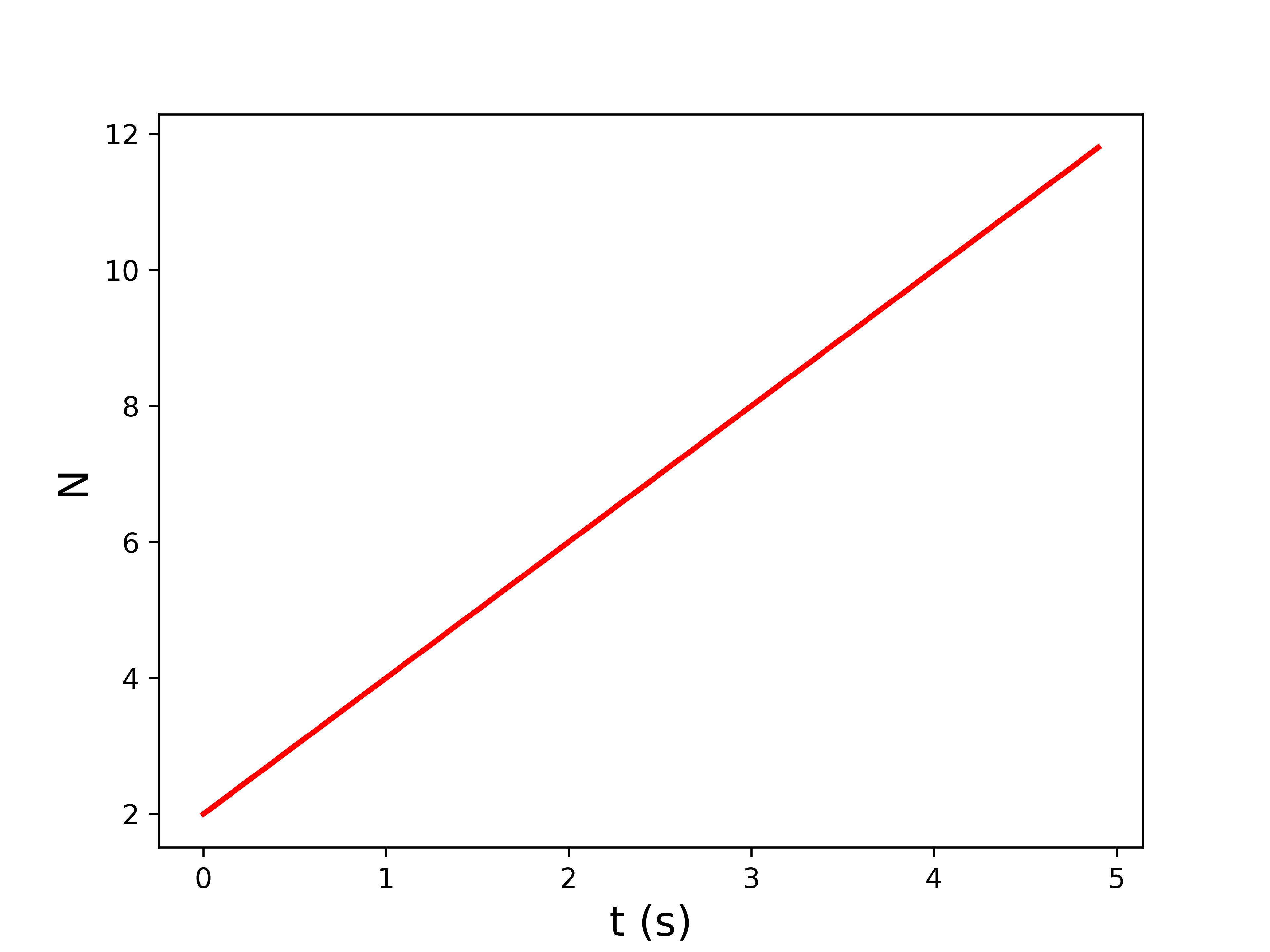
N(t) = 2 t + 2 \ \ \ (t \geqq 0)
でしょ?
人口モデルを数値的に解いたった
上で書いたマルサスモデルの微分方程式を数値的に解いてみましょう。
「人口の増加率(dP/dt)が人口(P)そのものに比例(m倍)する」
\frac{dP}{dt} = P
(簡単にするために比例係数m=1としています。)
ちなみにこの式は解析的に簡単に解けるもので、結果的に指数関数が得られます。
ですが、そこは知らないフリをして解いていきましょう。
数値的に解くには初期条件が必要になります。
遊び・勉強のために解くだけなら初期条件は別に何でもいいです。
とりあえず2015年時の大阪の人口が269万人らしいので、
P(0) = 269
としましょう。
これを解くと以下のようになります。
さっきのコードとあまり変わってません。ぜひ違いを見つけてください。
import matplotlib.pyplot as plt
import numpy as np
def difference(value, delta):
return value*delta
# 配列の準備
totlaNum = 50 # とりあえず50にしているだけ
time = np.zeros(totlaNum, dtype = float)
number = np.zeros(totlaNum, dtype = float)
# 初期値
time[0] = 0.0
number[0] = 269.0
deltaTime = 0.1 #
# 計算
for i in range(totlaNum-1):
# Δを足してるだけなんです。Gitであれば差分のコミットにあたるのがここです。
number[i+1] = number[i] + difference(number[i], deltaTime)
time[i+1] = time[i] + deltaTime
# plot
plt.plot(time, number, 'r-', lw = 2, color='red')
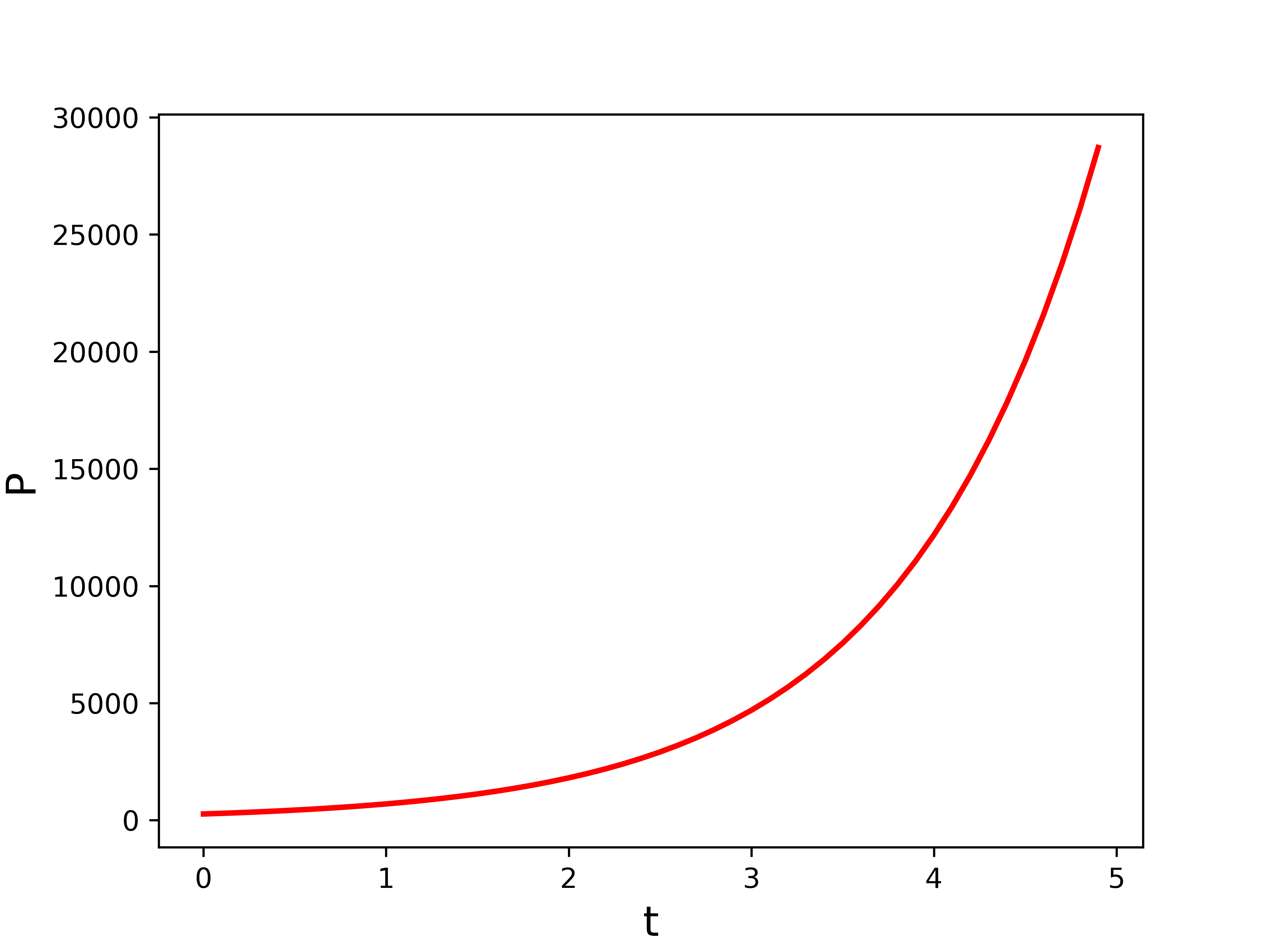
plt.xlabel('t', fontsize=15)
plt.ylabel('P', fontsize=15)
plt.savefig('malthusian_model.png', dpi=600)
# show
plt.show()
横軸の時間の単位を決めていませんので、どんな時間スケールかはわかりませんが、こんなに人口が膨れるのは直感的にもあり得ないですよね。
そうです。このマルサスモデルは修正が加えられています。
このように、最初に提案されたモデルが正しいとは限らないので
モデル(微分方程式)提案 → シミュレーション → 実データ収集 → モデルの改良(新モデルの提案) → ...
という繰り返しの中でモデルをブラッシュアップしていくのが一般的です。
数値シミュレーション(応用)
私は化学の専門ではないのですが、用例として最適だったので今回は化学反応についての数値シミュレーションを行ってみたいと思います。
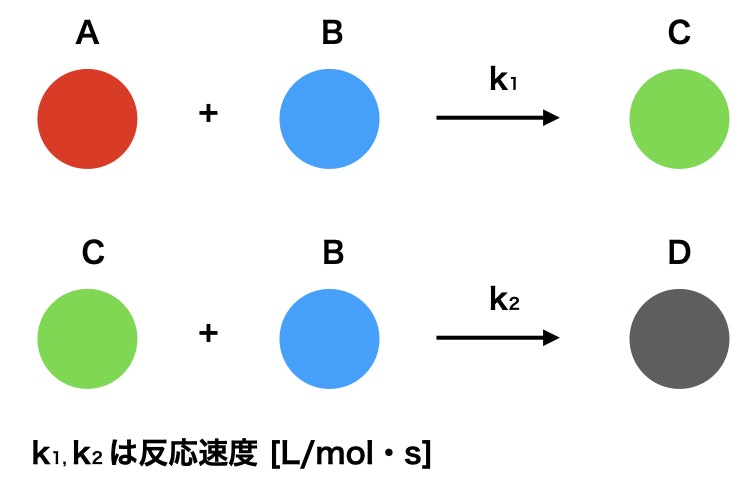
AとBの分子は反応速度定数k1でCを生成、
生成されたCとBの分子は反応速度定数k2でDを生成する
というモデルを考えます。
このモデルを微分方程式で表現してみましょう。
次のようになります。
\begin{aligned}
\frac{d[A]}{dt} &= - k_1 [A] [B] \\
\frac{d[B]}{dt} &= - k_1 [A] [B] - k_2 [B] [C] \\
\frac{d[C]}{dt} &= k_1 [A] [B] - k_2 [B] [C] \\
\frac{d[D]}{dt} &= k_2 [A] [B]
\end{aligned}
初期条件として、
AとBがそれぞれ100[mol/Ls], 120[mol/Ls]の濃度であるとします(てきとうです。)。
あと、反応速度定数k1, k2は未知なので、これもてきとうにそれぞれ0.0020[L/mols], 0.0010[L/mols]としておきます。
余談ですが、
反応速度定数は文献から引用するか(以前に誰かが調べてくれてるということ)、実際に実験して調べる必要があります。
import matplotlib.pyplot as plt
import numpy as np
"""
reactions:
A + B (k_1)-> C
C + B (k_2)-> D
differential equations:
dA/dt = - k_1 * A * B
dB/dt = - k_1 * A * B - k_2 * B * C
dC/dt = k_1 * A * B - k_2 * B * C
dD/dt = k_2 * B * C
variables:
velosity (dX/dt): [mol/L*s]
density (X): [mol/L]
reactRateConst (k): [L/mol*s]
"""
def calcVelocityA(reactRateConst1, densityA, densityB, delta):
return (- reactRateConst1 * densityA * densityB) * delta
def calcVelocityB(reactRateConst1, reactRateConst2, densityA, densityB, densityC, delta):
return (- reactRateConst1 * densityA * densityB - reactRateConst2 * densityB * densityC) * delta
def calcVelocityC(reactRateConst1, reactRateConst2, densityA, densityB, densityC, delta):
return (reactRateConst1 * densityA * densityB - reactRateConst2 * densityB * densityC) * delta
def calcVelocityD(reactRateConst2, densityB, densityC, delta):
return (reactRateConst2 * densityB * densityC) * delta
num = 500
time = np.zeros(num, dtype = float)
densityA = np.zeros(num, dtype = float)
densityB = np.zeros(num, dtype = float)
densityC = np.zeros(num, dtype = float)
densityD = np.zeros(num, dtype = float)
# 初期条件
densityA[0] = 100.
densityB[0] = 120.
densityC[0] = 0.
densityD[0] = 0.
# 反応速度定数
reactRateConst1 = 0.0020
reactRateConst2 = 0.0010
delTime = 0.2 # (s)
breakPoint = 0
for i in range(num-1):
if (densityA[i] <= 0.01):
print(i, "densityA is less than 0.01 !!")
breakPoint = i
break
if (densityB[i] <= 0.01):
print(i, "densityB is less than 0.01 !!")
breakPoint = i
break
densityA[i+1] = densityA[i] + calcVelocityA(reactRateConst1, densityA[i], densityB[i], delTime)
densityB[i+1] = densityB[i] + calcVelocityB(reactRateConst1, reactRateConst2, densityA[i], densityB[i], densityC[i], delTime)
densityC[i+1] = densityC[i] + calcVelocityC(reactRateConst1, reactRateConst2, densityA[i], densityB[i], densityC[i], delTime)
densityD[i+1] = densityD[i] + calcVelocityD(reactRateConst2, densityB[i], densityC[i], delTime)
time[i+1] = time[i] + delTime
# plot
plt.plot(time, densityA, 'r-', lw = 2, color='red')
plt.plot(time, densityB, 'r-', lw = 2, color='blue')
plt.plot(time, densityC, 'r-', lw = 2, color='green')
plt.plot(time, densityD, 'r-', lw = 2, color='black')
plt.xlim(0, time.max())
plt.xlabel('time (s)', fontsize=15)
plt.ylabel('densitys (mol/L)', fontsize=15)
plt.savefig('reactionKinetics.png', dpi=600)
# show
plt.show()
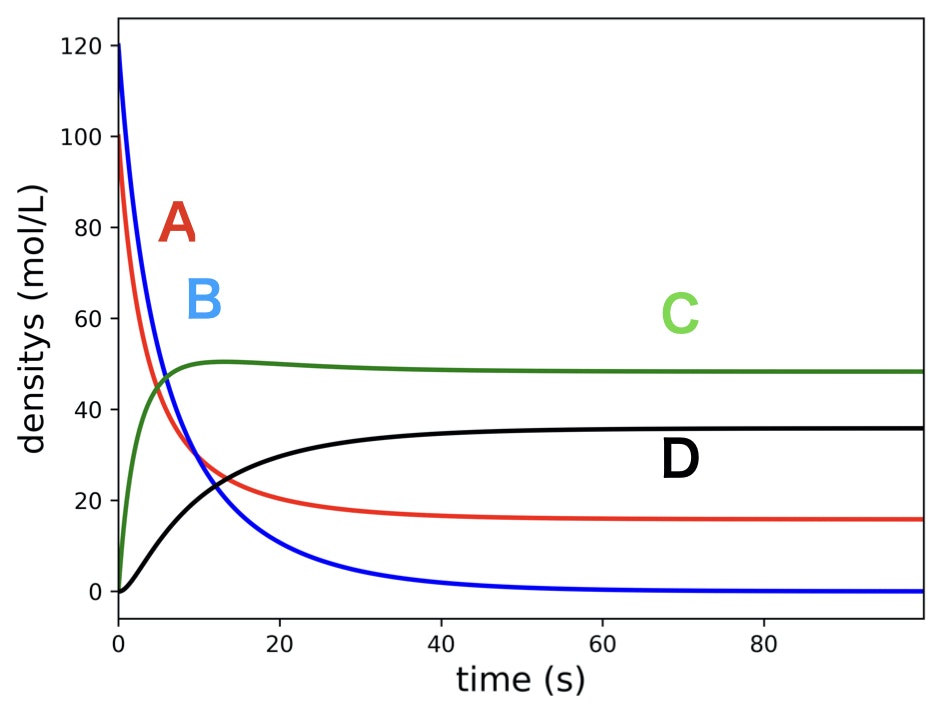
時間が経つにつれてAとBが急激に減少して、Cが急増し、Dがゆるやかに増加していくのがわかりますね!
ぜひ、初期値とか反応速度定数(k1, k2)を変えてグラフがどう変わるか確認して遊んでみてください。
さらに学びたい方へ
本記事では全微分方程式の非常に簡単なものだけを扱いました。
解き方に関しても誤差が大きい解き方になっています。
より正確な解を得たい方は、ルンゲクッタ法を学習するのが良いと思います。
それ以外にもオイラー法、ホイン法なども合わせて勉強すると良いと思います!
もっと難しい数値計算に手を出したいという方は、偏微分方程式の数値解法を学ぶと楽しいですよ〜。
熱拡散方程式とかを解いて、カラープロットで熱の拡散を描画したときにはテンションがあがりましたね。
めちゃめちゃ古い本ですが「偏微分方程式の数値解法入門」って本がおすすめです。
ソースコードがBASICで書かれているのが微妙なところですが、Pythonとかの別言語に自分で書き換えると勉強になります(なりました)。
この本が終われば、有限要素法について学ばれるのが良いかと思います。
あと、極座標系とか直交座標系以外で表された微分方程式も解けるようになると幅が広がります!