はじめに
普通の主成分分析だと,線形の相関のあるデータ(相関がなくても出来ますが相関があればなおいいぐらいの意味)の次元圧縮しかできません.
データを高次元に射影して,通常の主成分分析を行う,カーネル主成分分析では非線形の相関データを扱うことが可能になるという訳です.
普通の主成分分析は以下を参考にしてみてください.
https://qiita.com/NoriakiOshita/items/460247bb57c22973a5f0
カーネル主成分分析とは
カーネル関数とは
(半)正定値性を満たす関数($k:\mathcal{X} \times \mathcal{X} \to \mathbb{R}$)のことカーネル関数といいます.
集合$\mathcal{X}$の二つの要素$x,x^{'}$に対し,カーネル関数$k(x,x^{'})$はx,x^{'}それぞれの特徴ベクトルの内積
k(x,x^{'})=\phi(x)^{T}\phi(x^{'}) = \sum_{m=1}^d \phi_m(x)\phi_m(x^{'})
として定義される.
正定値性
$\mathcal{X}$を集合とするとき,正定値性とは以下の2条件を満たすカーネル $k:\mathcal{X} \times \mathcal{X} \to \mathbb{R}$を($\mathcal{X}$上の)正定値カーネル(positive definite kernel)といいます.
・対称性:任意の$x,y\in \mathcal{X}$に対し$k(x,y)=k(y,x)$
・正値性:任意の$n \in \mathbb{N},x_1, \dots , x_n \in \mathcal{X}, c_1, \cdots ,c_n \in \mathbb{R}$ に対し,
$\sum_{i,j=1}^n c_i c_j k(x_i, x_j) \geq 0$
正定値カーネルの定義で用いられる正値性は,数学的には対称行列の半正定値性と呼ばれます.これはカーネル法の分野の習慣のために正定値カーネルと呼ばれる訳です.
グラム行列
行列Aに対して$A^TA$という行列をグラム行列といいます.
また,カーネル法で扱うデータ分析におけるグラム行列とは以下のようなものをいいます.
K=\left(
\begin{array}{ccc}
k(x_1,x_1) & k(x_2,x_1) & \cdots & k(x_n,x_1) \\
k(x_1,x_2) & k(x_2,x_2) & \cdots & k(x_n,x_2) \\
\vdots & \vdots & \ddots & \vdots \\
k(x_1,x_n) & k(x_2,x_n) & \cdots & k(x_n,x_n)
\end{array}
\right)
カーネルを設計するということはこのグラム行列を計算することと等しいです.(詳しくは参考文献を読んでください.)
再生核ヒルベルト空間
ヒルベルト空間Hとは
再生核ヒルベルト空間に行く前にまずヒルベルト空間の定義です.
ヒルベルト空間$\mathcal{H}$(または単に$\mathcal{H}$とも書く)は以下の内積の公理を満たすベクトル空間$\in\mathbb{R}$であるとする.
関数$\langle\cdot,\cdot \rangle_\mathcal{H}:\mathcal{H} \times \mathcal{H} \to \mathbb{R}$はヒルベルト空間$\mathcal{H}$の内積とする.
(ちなみに$\langle \rangle$はブラケット記法といいよく量子力学などで使われる記法です.ブラベクトル(左の括弧)とケットベクトル(右括弧)の内積を表してます.)
また,次の条件を満たします.
1.線形性:$\langle \alpha_1 f_1 + \alpha_2 f_2,g\rangle_\mathcal{H} = \alpha_1 \langle f_2,g\rangle_\mathcal{H} + a_2\langle f_2,g\rangle_\mathcal{H}$
2.対称性:$\langle f,g \rangle_\mathcal{H} = \langle g,f\rangle_\mathcal{H}$
3.正値性:$\langle f,f \rangle_\mathcal{H} \geq 0 かつ \langle f,f \rangle_\mathcal{H} = 0 \quad f=0$のときになりたつ.
またノルムを以下のように定義することが出来る.
$||f||_\mathcal{H} := \sqrt{ \langle f,f \rangle _\mathcal{H} }$によってfのノルムの定義が出来ました.
このように内積をとることが出来る空間の事をヒルベルト空間といいます.(ここでは,完備性については議論しないこととします.)
再生核ヒルベルト空間とは
やっと再生核ヒルベルト空間です.カーネル法で一番重要な空間です.
上で定義したカーネル関数の定義を思い出してください.上にスクロールするのも面倒だと思うのでもう一度張ります.
k(x,x^{'})=\langle \phi(x)^{T}\phi(x^{'}) \rangle _\mathcal{H}
これがカーネル関数でした.このとき再生核ヒルベルト空間では次の性質を持ちます.
1.任意の$x$に関して,$k(\cdot,x)\in \mathcal{K}$
2.任意の関数$f\in\mathcal{K}$に対して,$f(x)= \langle f, k(\cdot,x) \rangle _\mathcal{K}$
特に2を再生性といいます.
$\mathcal{K}$はパラメータベクトルと特徴ベクトルの内積で定義される関数の全体の集合です.
定理の中の再生性は,$\mathcal{K}$の中の任意の関数fとカーネル関数の内積がその関数の値になるという特徴的な性質があります.これが再生核ヒルベルト空間と呼ばれるゆえんであり,特にヒルベルト空間$\mathcal{K}$を再生核ヒルベルト空間(RKHS:Reproducing Kernel Hilbert Space)といいます.また,カーネル関数kのことをその再生核といいます.
動画による理解
カーネルサポートベクトルマシンの動画で再生核ヒルベルト空間へデータを射影(多項式カーネルを用いて)してデータを分離する超平面を求めている動画になります.
SVM with polynomial kernel visualization https://t.co/gK1uTm2NRn @YouTubeさんから
— NoriakiOshita (@whisponchan) 2018年5月11日
正定値カーネルの例
m次元ユークリッド空間$\mathbb{R}^m$上の正定値カーネルの例を示します.
・指数型
k_E(x,y)=exp(\beta x^{T}y) \quad (\beta > 0)
・ガウスRBF(radial basis function)カーネル
k_G(x,y)=exp(-\frac{1}{2\sigma^2}||x-y||^2) \quad (\sigma>0)
・ラプラスカーネル
k_L(x,y)=exp(-\alpha \sum_{i=1}^n |x_i-y_i|) \quad (\alpha > 0)
・多項式カーネル
k_P(x,y) = (x^{T}y+c)^d \quad (c \geq0,d\in \mathbb{N})
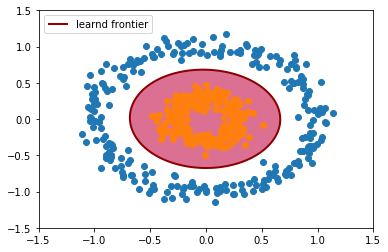
動画は多項式カーネルですが,動画のようには上手くいかなかったのでガウシアンカーネルで識別境界を学習(learnd frontier)させました.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn import svm
from sklearn.svm import LinearSVC
np.random.seed(0)
xx, yy = np.meshgrid(np.linspace(-1.5, 1.5, 500), np.linspace(-1.5, 1.5, 500))
X, y = make_circles(n_samples=400, factor=.3, noise=.05)
# 線形サポートベクトルマシン
linear_svc = LinearSVC(random_state=0)
# ガウスカーネルサポートベクトルマシン
rbf_svc = svm.SVC(kernel='rbf')
rbf_svc.fit(X, y)
linear_svc.fit(X, y)
# plot the line, the points, and the nearest vectors to the plane
Z = rbf_svc.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
a = plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors='darkred')
plt.contourf(xx, yy, Z, levels=[0, Z.max()], colors='palevioletred')
X, y = make_circles(n_samples=500, factor=.3, noise=.08)
y_rbf = rbf_svc.predict(X)
plt.scatter(X[y_rbf==0,0],X[y_rbf==0,1])
plt.scatter(X[y_rbf==1,0],X[y_rbf==1,1])
plt.legend([a.collections[0]],
["learnd frontier"],
loc="upper left",)
カーネル主成分分析のプログラム
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA, KernelPCA
from sklearn.datasets import make_circles
np.random.seed(0)
X, y = make_circles(n_samples=400, factor=.3, noise=.05)
kpca = KernelPCA(kernel="rbf", fit_inverse_transform=True, gamma=10)
X_kpca = kpca.fit_transform(X)
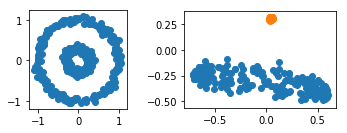
plt.subplot(2, 2, 1, aspect='equal')
plt.scatter(X[:,0],X[:,1])
plt.subplot(2, 2, 2, aspect='equal')
plt.scatter(X_kpca[y==1,0],X_kpca[y==1,1])
plt.scatter(X_kpca[y==0,0],X_kpca[y==0,1])
左が元の図で右がカーネル主成分分析で次元圧縮したものとなります.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.decomposition import PCA, KernelPCA
from sklearn.datasets import make_circles
from sklearn.datasets.samples_generator import make_swiss_roll
np.random.seed(0)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
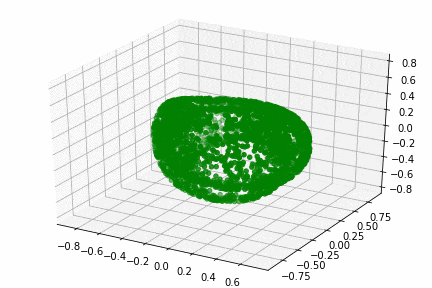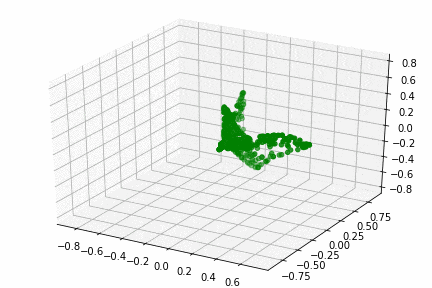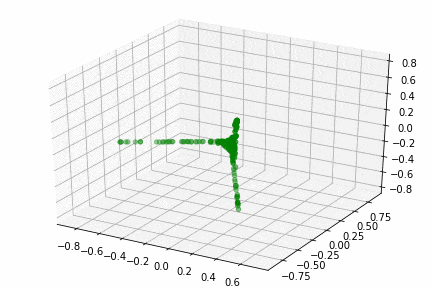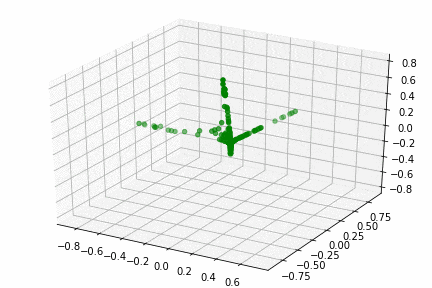
X, _ = make_swiss_roll(n_samples=1500, noise=0.05)
# 元のスイスロールを描画
# ax.scatter(X[:,0],X[:,1],X[:,2])
kpca = KernelPCA(kernel="rbf", fit_inverse_transform=True, gamma=2)
X_kpca = kpca.fit_transform(X)
ax.scatter(X_kpca[:,0],X_kpca[:,1])
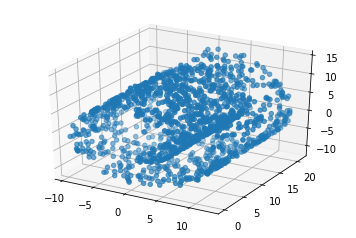
元のスイスロール
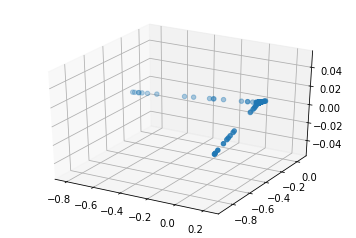
カーネル主成分分析で次元圧縮されたスイスロール
一般的にgamma値を変えることによって形が大きく変化していきます.
gammaの値を0.01から2.0まで変化させるアニメーションが以下になります.
まとめ
カーネル主成分分析は今回はガウスRBFを用いました.$\sigma$の値を変化させることにより次元圧縮の様子がかなり変化してしまいます.(sklearnの場合はgammaの値を変えることによって.)
データによってカーネル関数を変える必要があります.
単純に応用に使いたいならt-sneやUMAPを使えば良いのかなと思います.
理論的なことがこの記事では中途半端になっているため,時間があるときに補足していこうと思います.
参考
カーネル法入門:福水健次
福水先生のこちらの本は理論的にとても詳しく正定値カーネルについて書かれています.大変参考にさせていただきました.
理論的にきっちりやりたい場合はこちらの福水先生の本を参考にすると良いと思います.
カーネル多変量解析:赤穗昭太郎
赤穗先生の本はイラストと文章による説明が福水先生の本よりも多いためカーネル法のイメージをつかむために大変役に立ちました.
Introduction to RKHS, and some simple kernelalgorithms
http://www.gatsby.ucl.ac.uk/~gretton/coursefiles/lecture4_introToRKHS.pdf
グラム行列の意味と半正定値性
https://mathwords.net/gramgyoretu