最適化手法について(最急降下法をなるべく簡単に説明)

目的

• 最急降下法についてあんまり知らない人にも説明するため
• 自身の理解度も深めるため

説明内容

• 最急降下法とは
• 更新する方法について
• 微分とは
• 具体例
• まとめ

最急降下法とは

• 最適化アルゴリズムで勾配降下法の1つ
• ある関数の最小値を求める手法である
• 簡単に言うと、ある関数のある変数に関する傾きを求め、その傾きを頼りにその変数を更新し、関数を最適化していく方法

例えばこんな感じ
ある関数が$y=x^2$だとすると

この傾きを使って$y$が$0$になるように$x$を最適化していくイメージ

更新する方法について

最急降下法を数式で表すと以下のような式になる

$$
x_{t+1} = x_t - \alpha \nabla f(x_t)
$$

• $x_{t+1}$ : 更新される値
• $x_t$ : 現時点の値
• $\alpha$ : 学習率
• $\nabla f(x_t)$ : 現時点での$f(x_t)$の微分
• $f(x)$ : 最適(最小)にしたい関数

ここで重要なのが微分です(この後の項目で説明します)
微分をすると先ほどの説明であったある関数の傾きを求められるようになります

学習率というのは簡単に言うと更新する量を調整するパラメータになります
例えば、傾きが大きいと更新される値も大きくなり、更新される幅が傾きだけに依存してしまいます
なので学習率というものを使って更新する幅を調整します

微分とは

微分の定義を以下に表します
$$
\nabla f(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}
$$
ここで$\lim_{h \to 0}$というものが出てきましたが、これは$h$を限りなく$0$に近づけるよという意味になります

$h$はとーーっても小さい値ということになります

つまり、微分とは
現時点からちょっと変化した$f(x+h)$と
現時点の$f(x)$の差を計算し
ちょっと変化させた分で除算をしています

つまり、ちょっと変化させたらどれだけ変化するかな？という変化量を見ていいることになります
これを傾きと読んだりしています

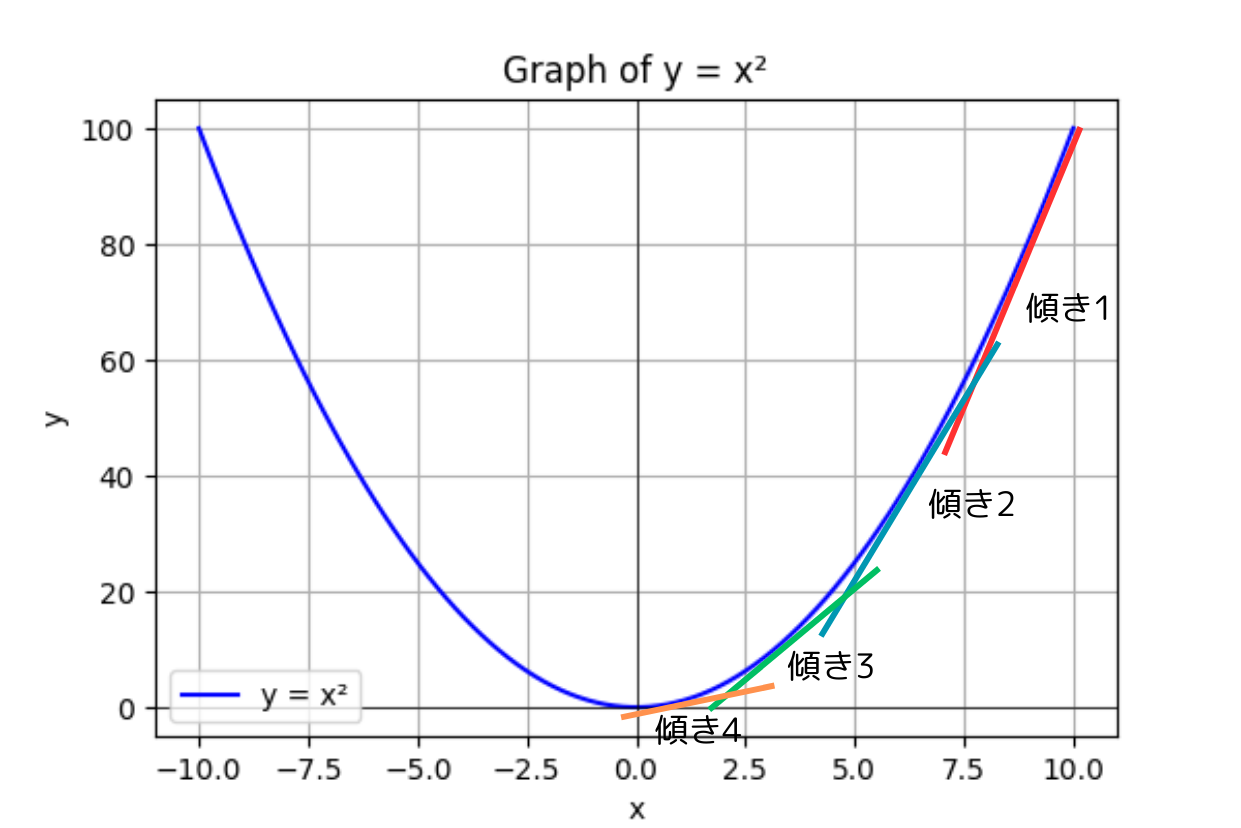
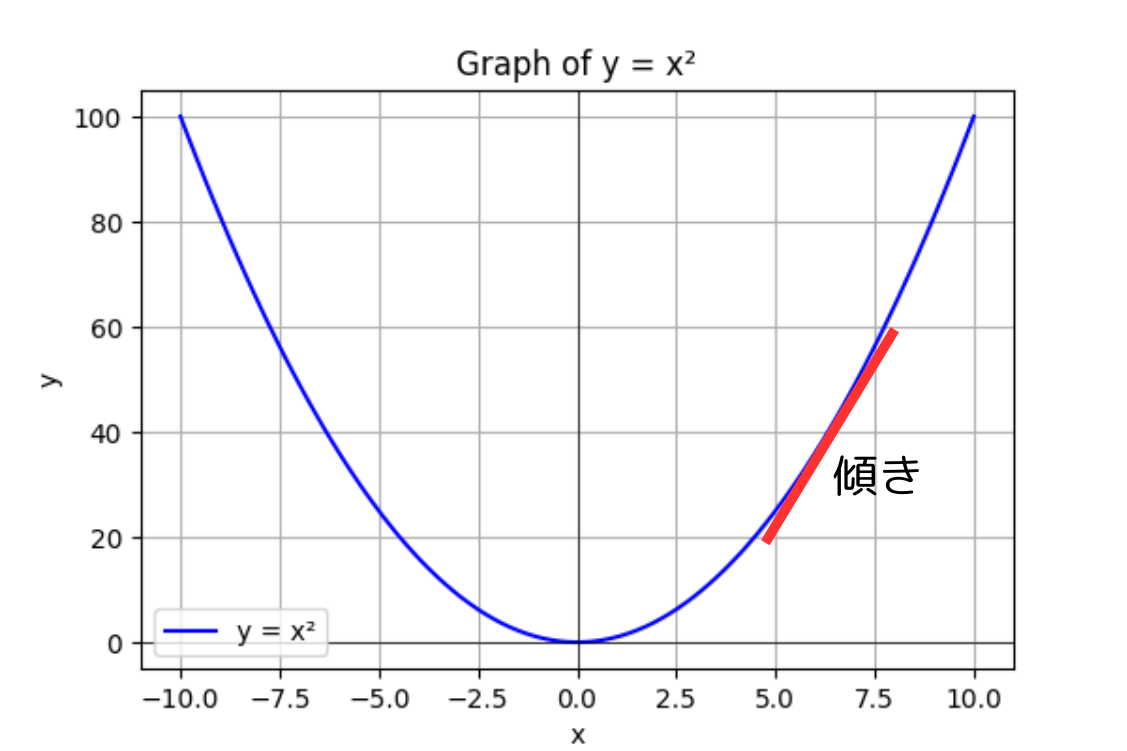
例として$f(x)=x^2$の図を用意しました

微分のイメージは上記のような感じです

これで最急降下法を使うための材料が集まったと思います
あとは、自分が最適にしたい関数、変数を用意すれば、最急降下法を試すことができます

具体例

今回は具体例として$f(x,y) = (x-2)^2 + (y+4)^2$を最適化していこうと思います

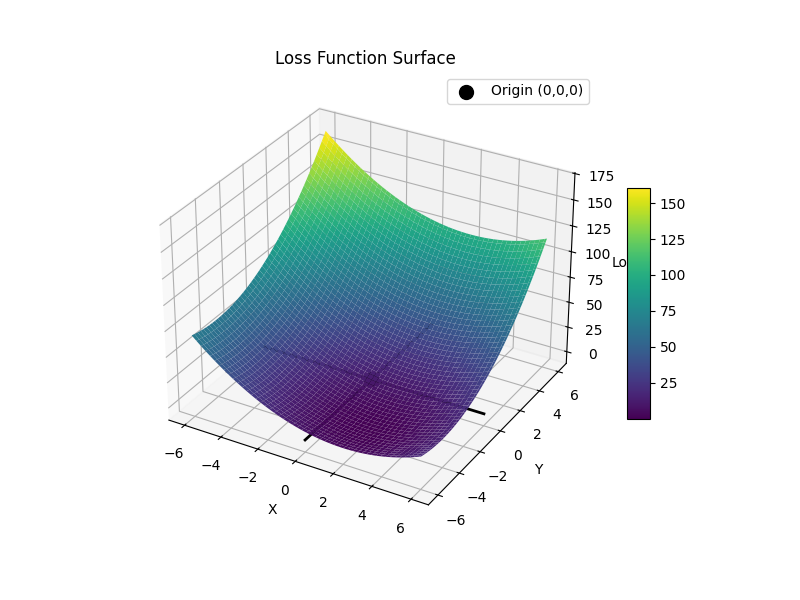
$f(x,y) = (x-2)^2 + (y+4)^2$をグラフで表すと以下のようになります

式からも分かっちゃうんですが、$x$は正の方向、$y$は負の方向にずらしていくと値が0に近づいていることが分かります

実際に最急降下法を実装しました(pythonです)
ひとまず全コードを載せます(適当に作ったので汚いです、すみません)

import numpy as np


def loss_function(x, y):
    loss = ((x - 2)**2 + (y + 4)**2)
    loss = np.sqrt(loss**2)

    return loss


def diff_loss_function(loss_function, x, y, diff_symbol: str, h=1e-6):
    if diff_symbol == "x":
        diff = (loss_function(x + h, y) - loss_function(x, y)) / h
    elif diff_symbol == "y":
        diff = (loss_function(x, y + h) - loss_function(x, y)) / h
    else:
        diff = 0
        print("error")
    return diff


def calc_gradient_descent(loss_function, diff_loss_function, initial_x, initial_y, alpha, error=1e-6):
    optimized_x = initial_x
    optimized_y = initial_y
    loss = loss_function(optimized_x, optimized_y)

    iteration = 100000
    for i in range(iteration):
        if loss < error:
            print("optimized")
            break

        diff_x = diff_loss_function(loss_function, optimized_x, optimized_y, "x")
        diff_y = diff_loss_function(loss_function, optimized_x, optimized_y, "y")

        optimized_x = optimized_x - alpha * diff_x
        optimized_y = optimized_y - alpha * diff_y

        loss = loss_function(optimized_x, optimized_y)

    return optimized_x, optimized_y


def main():
    x, y = calc_gradient_descent(loss_function, diff_loss_function, 5, 5, alpha=0.001, error=1e-6)
    print("loss: ", loss_function(x, y), "x: ", x, "y: ", y)


if __name__ == "__main__":
    main()

最適化したい関数の定義

まずは最適化したい関数の定義
この関数のことを損失関数だったり、loss関数など呼ばれたりもしています

def loss_function(x, y):
    loss = ((x - 2)**2 + (y + 4)**2)
    loss = np.sqrt(loss**2)

    return loss

まずは最適化したい関数の計算
二乗したあとにルートをつける二乗平均平方根誤差を計算してます
こうすることで必ず正の値になります(誤差の大きさが求められる)

微分計算の定義

def diff_loss_function(loss_function, x, y, diff_symbol: str, h=1e-6):
    if diff_symbol == "x":
        diff = (loss_function(x + h, y) - loss_function(x, y)) / h
    elif diff_symbol == "y":
        diff = (loss_function(x, y + h) - loss_function(x, y)) / h
    else:
        diff = 0
        print("error")
    return diff

ここでは何の変数に関する微分をしたいかをまず決めています
$x$に関する微分の場合、今の$x$の値に$h$という微小な値を与えてます
微分の定義とは少し異なりますが、ほとんど問題ないと思います(定義では0に限りなく近づけるということになっている)
この微小変化させる量は任意です

あとは微分の定義のままです
$x$についての微分を求めるとき

• 現在の値$x$に$h$を加えた$x+h$と現在の値$y$を使った時の関数の値
• 現在の値$x, y$を使った時の関数の値
• 上記の差を計算し、$h$で除算

最急降下法の更新式定義

def calc_gradient_descent(loss_function, diff_loss_function, initial_x, initial_y, alpha, error=1e-6):

ここが最も重要なところです
まずは以下の内容を決める必要があります

• どんな関数を最適化したいか

• 変数の初期値は何か

• 学習率はどうするか

• 許される誤差の値

• どんな関数を最適化したか

  • 今回は$f(x,y) = (x-2)^2 + (y+4)^2$になります

• 変数の初期値は何か

  • 今回は$x$, $y$どちらも5にしました

• 学習率

  • 今回は0.001になっています
  • だいたいこのくらいの値が使われます

• 許される誤差

  • 完全に0にするのは難しいので、許容される誤差を決めます
  • 今回は$10^{-6}$を使っています

更新式の定義

    optimized_x = initial_x
    optimized_y = initial_y
    loss = loss_function(optimized_x, optimized_y)

    iteration = 100000
    for i in range(iteration):
        if loss < error:
            print("optimized")
            break

        diff_x = diff_loss_function(loss_function, optimized_x, optimized_y, "x")
        diff_y = diff_loss_function(loss_function, optimized_x, optimized_y, "y")

        optimized_x = optimized_x - alpha * diff_x
        optimized_y = optimized_y - alpha * diff_y

        loss = loss_function(optimized_x, optimized_y)

    return optimized_x, optimized_y

最急降下法の定義のままですね

• 現時点の変数$x$, $y$に関する微分を行う
• 現時点の値から$\alpha * \nabla f(x,y)$の差を取って新しい値へ更新する
• あとは許容誤差まで変数を更新し続けます
• 収束しなかった場合は100000回で強制的に更新終了するようにしています

実際に実行した結果

実行すると赤い点が求まります
$x=2$, $y=-4$ですね

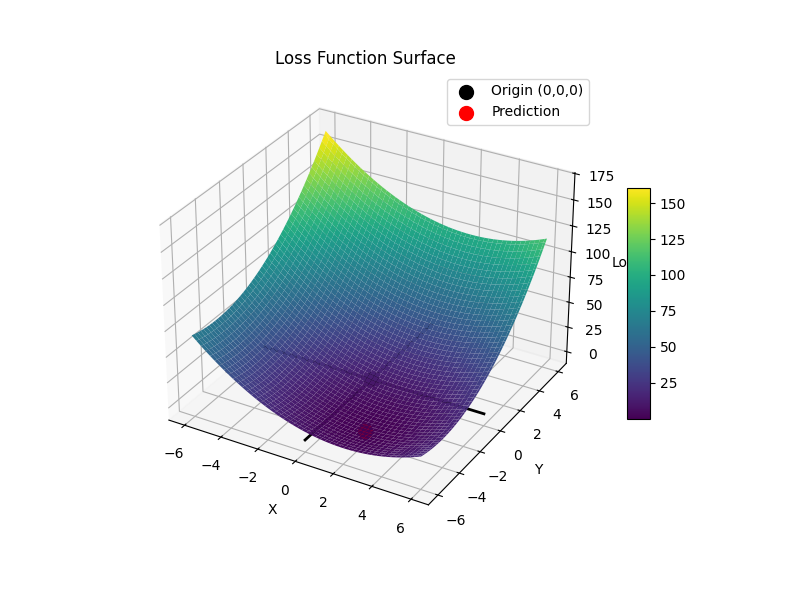
このようにして関数内にある変数の最適な値が求まります

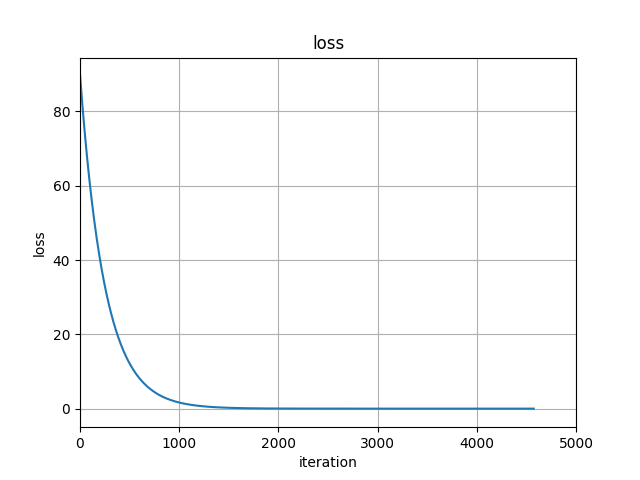
誤差の値をプロットしてみるとだんだん小さくなっていることが分かります

まとめ

今回は最急降下法についてまとめてみました
自分なりに、微分を知らない人でも伝わるよう説明してみました
伝わっていなかったらすみません
最急降下法は最適化手法の中で最も基礎な部分です
この手法からいろいろな派生版ができているのでこの仕組みさえ理解できれば、ほかの手法の理解も進めやすくなると思います
例えば、モーメンタム法やRMSProp、Adamなどが派生版に当たります
これをきっかけに最適化手法について少しでも興味を持っていただけたら嬉しいです

読んでいただきありがとうございました