逆運動学の最初の一歩。これができるとロボットをやってる感じが出る。
逆運動学の最初の一歩。これができるとロボットをやってる感じが出る。
やること
2本のアームと2つの回転軸からなる平面上のアームロボットについて、
与えられた座標にアームの先端が来るような軸の角度を逆運動学の計算で求めます。
難易度
高校の数Iぐらいのレベルです。
(三角関数、逆三角関数のごく初歩的な解説は省いています。)
[Qiita]この記事を書いたあとで余弦定理を使う方法を教えてもらい、記事にしてしみました。
そちらの方がわかりやすいと思います。
・次回記事:IK 逆運動学 入門:2リンクのIKを解く(余弦定理)
・次次回記事:IK 逆運動学 入門:Processing3で2リンクアームを逆運動学で動かす
参考
・Tajima Robotics:2リンクモデルの逆運動学を求める!順運動学の式から算出する方法
・mathcentreJune11,2004
当記事は、ほぼ上記2つの記事を組み合わせたような内容で、それを理解するためのメモになります。
余弦定理を使ったシンプルバージョンは下記になります。
・IK 逆運動学 入門:2リンクのIKを解く(余弦定理)
ステップ1: 順運動学を理解する
まず順運動学を考えます。
順運動学はアームの長さと角度を与えた場合に、先端がどの座標を示すかを計算するものです。
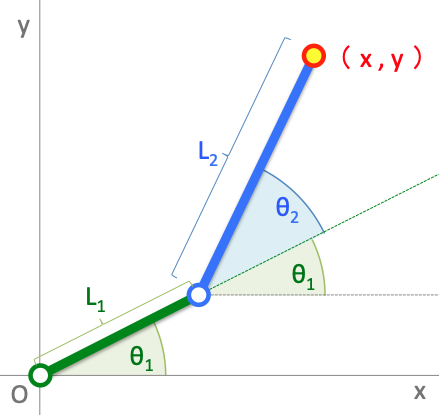
図のように緑のアームと青のアームが回転軸で接続されている時、先端の座標は、
\\
x = L_1\cos(\theta_1) + L_2\cos(\theta_1+\theta_2)\\
y = L_1\sin(\theta_1) + L_2\sin(\theta_1+\theta_2)
となります。この説明は省きます。
ステップ2: 式変形でθを整理する
いよいよ本題の逆運動学です。
逆運動学(IK,Inverse Kinematics)にはいろいろな方法があるようですが、幾何学的に求める基本的な方法で解いていきます。
順運動学の式をあの手この手で変形して、使いやすい形になるように整えていくアプローチになります。
2リンクの順運動学の式は下記のように表すことができます\\
\\
x = L_1\cos(\theta_1) + L_2\cos(\theta_1+\theta_2)\\
y = L_1\sin(\theta_1) + L_2\sin(\theta_1+\theta_2)\\
\\
この式を変形してθ_1のみで表せるように整理していきます\\
cos^2\alpha+sin^2\alpha=1 の公式を利用すればθ_2を消せそうなので、\\
まず移項してみます\\
\\
x - L_1\cos(\theta_1) = L_2\cos(\theta_1+\theta_2)\\
y - L_1\sin(\theta_1) = L_2\sin(\theta_1+\theta_2)\\
\\
両辺を二乗します\\
\\
x^2 - 2xL_{1}\cos(\theta_1) + \,L_1\!^2\cos^2(\theta_1) = L_2\!^2\cos^2(\theta_1+\theta_2)\\
y^2 - 2yL_{1}\sin(\theta_1) + \,L_1\!^2\sin^2(\theta_1) = L_2\!^2\sin^2(\theta_1+\theta_2)\\
\\
左辺同士、右辺同士をそれぞれ足します\\
\\
x^2 +y^2- 2xL_{1}\cos(\theta_1) - 2yL_{1}\sin(\theta_1) + \,L_1\!^2\cos^2(\theta_1) + \,L_1\!^2\sin^2(\theta_1) \\= L_2\!^2\cos^2(\theta_1+\theta_2) + L_2\!^2\sin^2(\theta_1+\theta_2)\\
\\
共通項でくくります\\
\\
x^2 +y^2- 2L_{1}(x\cos(\theta_1) - y\sin(\theta_1)) + \,L_1\!^2(\cos^2(\theta_1) + \sin^2(\theta_1)) \\
= L_2\!^2(\cos^2(\theta_1+\theta_2) + \sin^2(\theta_1+\theta_2))\\
\\
ここで\,cos^2\alpha+sin^2\alpha=1 より \\
\\
x^2 +y^2- 2L_{1}(x\cos(\theta_1) - y\sin(\theta_1)) + \,L_1\!^2 \\
= L_2\!^2\\
\\
となり、\theta_2 が消せました。うれしいですね。\\
さらにスッキリさせるために\,\theta_1を含む項を左辺にまとめると\\
\\
2L_{1}(x\cos(\theta_1) + y\sin(\theta_1))=x^2 +y^2 + \,L_1\!^2 -L_2\!^2 \\
\\
x\cos(\theta_1) + y\sin(\theta_1)
=\frac{x^2 +y^2 + \,L_1\!^2 -L_2\!^2}{2L_1} \,\,\,\,\,・・・②\\
\\
となります。\\
この後、なんとかx,y,L_1,L_2だけで\theta_1が求められるように\\
ステップ3で x\cos(\theta_1) + y\sin(\theta_1)\,を解いていきます。
ステップ3: 合成公式と逆三角関数の理解
\\
実は、x\cos(\theta_1) + y\sin(\theta_1)\,は三角関数の合成公式により、\\
下記のように表すことができます\\
\\
x\cos(\theta_1) + y\sin(\theta_1) =\sqrt{x^2+y^2}\cos(\theta_1- \arctan(\frac{y}{x})) \,\,\,\,\,・・・③\\
\\
三角関数の合成、解き方については長くなりますがこの記事で一番大事なところなので説明を畳んでおきます。(左の黒三角をクリックしてください。)
\\
この合成公式を導くために、一旦\\
\\
A\,\cos X + B\,\sin X = R\,\cos(X- \alpha)\\
\\
について考えます。\\
\\
加法定理より\\
R\,\cos(X- \alpha)= R\,(\cos X \cos \alpha + \sin X \sin \alpha)\\
\\
変形すると\\
R\,\cos(X- \alpha)= (R\,\cos \alpha) \cos X + (R\sin \alpha) \sin X\\
\\
ここで、\\
A = (R\,\cos\alpha) \\
B = (R\,\sin\alpha)\\
とおくと\\
\\
R\,\cos(X- \alpha) = A\,\cos X + B\,\sin X \,\,\,\,\,・・・④\\
と表すことができます\\
\\
また、 \\
\begin{align}
A^2 + B^2&= (R\,cos α)^2 + (R\,sin α )^2\\
&= R^2 (cos^2 α) + R^2( sin^2 α )\\
&= R^2 (cos^2 α + sin^2 α )\\
&= R^2\\
\end{align}\\
\\
R= \pm\sqrt{A^2 + B^2}\\
\\
道筋を1つに決定するために、プラスの解を採用すると、 \\
\\
R= \sqrt{A^2 + B^2} \,\,\,\,\,・・・⑤\\
\\
\\
一方、\alpha について考えると、 \\
\\
\frac{B}{A}=\frac{\sin\alpha}{\cos\alpha}=\tan\alpha\\
\\
\alpha = \arctan(\frac{B}{A}) \,\,\,\,\,・・・⑥\\
\\
※ここで式を変形させるために逆三角関数を使っていますが、\\
なんのことかわからないという場合は検索で調べてみてください。\\
\\
④⑤⑥より、 \\
\\
A\,\cos X + B\,\sin X = R\,\cos(X-\alpha)\\
= \sqrt{A^2 + B^2}\cos(X-\arctan(\frac{B}{A}))\\
\\
A=x,B=y,X=\theta_1を上の公式にあてはめると、\\
x\cos(\theta_1) + y\sin(\theta_1) =\sqrt{x^2+y^2}\cos(\theta_1- \arctan(\frac{y}{x})) \,\,\,\,\,・・・③\\
が導かれる\\
ステップ4: θ1を求める
x\cos(\theta_1) + y\sin(\theta_1)
=\frac{x^2 +y^2 + \,L_1\!^2 -L_2\!^2}{2L_1} \,\,\,\,\,・・・②\\
x\cos(\theta_1) + y\sin(\theta_1) =\sqrt{x^2+y^2}\cos(\theta_1- \arctan(\frac{y}{x})) \,\,\,\,\,・・・③\\
\\
より\\
\\
\sqrt{x^2+y^2}\cos(\theta_1- \arctan(\frac{y}{x}))=\frac{x^2 +y^2 + \,L_1\!^2 -L_2\!^2}{2L_1}\\
cos(\theta_1- \arctan(\frac{y}{x}))=\frac{x^2 +y^2 + \,L_1\!^2 -L_2\!^2}{2L_1\sqrt{x^2+y^2}}\\
\theta_1- \arctan(\frac{y}{x})=\pm\arccos(\frac{x^2 +y^2 + \,L_1\!^2 -L_2\!^2}{2L_1\sqrt{x^2+y^2}})\\
\theta_1=\pm\arccos(\frac{x^2 +y^2 + \,L_1\!^2 -L_2\!^2}{2L_1\sqrt{x^2+y^2}})+ \arctan(\frac{y}{x}) \,\,\,\,\,・・・⑦\\
\\
これで、\theta_1が求まります。\\
\\
ステップ5: θ2を求める
最後に\theta_2を求めます。\\
\\
先に求めた順運動学の方程式\\
\\
x - L_1\cos(\theta_1) = L_2\cos(\theta_1+\theta_2)\\
y - L_1\sin(\theta_1) = L_2\sin(\theta_1+\theta_2)\\
\\
について2つ目の式を1つ目の式で割ると \\
\\
\begin{align}
\frac{y - L_1\sin(\theta_1)}{x - L_1\cos(\theta_1)}&=\frac{L_2\sin(\theta_1+\theta_2)}{L_2\cos(\theta_1+\theta_2)}
\\
\\
&=\tan(\theta_1+\theta_2) \\
\end{align}\\
\\
となるので、\theta_2について解くと、\\
\\
\tan(\theta_1+\theta_2) = \frac{y - L_1\sin(\theta_1)}{x - L_1\cos(\theta_1)} \\
\\
\\
\theta_1+\theta_2 = \arctan(\frac{y - L_1\sin(\theta_1)}{x - L_1\cos(\theta_1)})\\
\\
\theta_2 = \arctan(\frac{y - L_1\sin(\theta_1)}{x - L_1\cos(\theta_1)})-\theta_1 \,\,\,\,\,・・・⑧\\
\\
となり、\,\theta_2も決定します。 \\
ステップ6: 式のまとめ
これで、アームの先端座標x,yとアームの長さL_1,L_2決まっていれば、\\
2つのリンクの角度を求めることができるようになります。 \\
\\
\theta_1=\pm\arccos(\frac{x^2 +y^2 + \,L_1\!^2 -L_2\!^2}{2L_1\sqrt{x^2+y^2}})+ \arctan(\frac{y}{x}) \,\,\,\,\,・・・⑦\\
\\
\theta_2 = \arctan(\frac{y - L_1\sin(\theta_1)}{x - L_1\cos(\theta_1)})-\theta_1 \,\,\,\,\,・・・⑧\\
\\
複数解となるので、⑦の\arccosはプラスかマイナスの\\
どちらか一方に固定しておくと便利かも。\\
また、arctanの範囲は-\pi/2 から \pi/2 の間に限定されるのでそこも注意。\\
次回
次回以降でこれをよりシンプルな余弦定理で解いたり、またProcessing3のスケッチにしてシミュレーション上の挙動を見たりしてみたいと思います。
・次回記事:IK 逆運動学 入門:2リンクのIKを解く(余弦定理)
・次次回記事:IK 逆運動学 入門:Processing3で2リンクアームを逆運動学で動かす
へんなところがあったらご指摘ください。