IK 逆運動学 入門：Processing3で2リンクアームを逆運動学で動かす

いよいよ逆運動学をプログラムで動かしてみるぞ

##やること
２本のアームと２つの回転軸からなる平面上のアームロボットをシミュレートします。
与えられた座標にアームの先端が来るような軸の角度を逆運動学の計算で求め、
Processing上にその結果を描画します。

そもそもの逆運動学の基本、計算方法については下記にまとめてみました。
・前回記事：IK 逆運動学 入門：２リンクのIKを解く（余弦定理）
・前前回記事：IK 逆運動学 入門：２リンクのIKを解く（合成公式）

##考え方

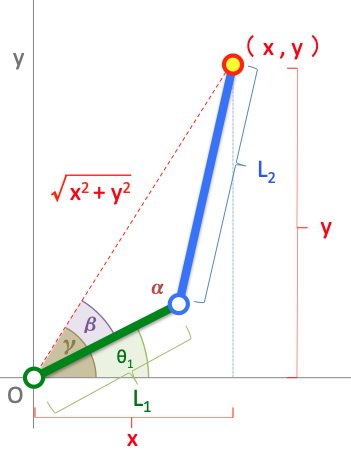
このスケッチでは図のように余弦定理を使って逆運動学を計算しています。
図の詳しい解説については前回記事にあります。こちらをクリック

Processing3のスケッチ

2本のアームそれぞれの角度を逆運動学で算出してから、アームの長さと角度をもとにアームの中継点と終端の座標を求め、線で結ぶ事で描画します。
アームの長さはスライダーで変更することができ、アームの終端が移動できる範囲も同時に描画するプログラムになっています。

Procesing3

import controlP5.*; //スライダー用のライブラリをインポート
ControlP5 cp5; //スライダーのインスタンスを作る

int arm1_length ; //アーム1の長さ
int arm2_length ; //アーム2の長さ
float arm1_angle; //アーム1の角度
float arm2_angle; //アーム2の角度

void setup() {
  size(400, 400); //画面サイズ
  strokeWeight(4); //アーム描画の線の太さ
  cp5 = new ControlP5(this); //スライダーを導入

  cp5.addSlider("arm1_length") //アーム1用の長さを決めるスライダー
    .setRange(10, 200) //アーム1用の長さを決めるスライダー
    .setValue(100)//アーム1の長さ（arm1_length = 100）
    .setPosition(60, 330) //スライダーの座標
    .setSize(70, 20); //スライダーのサイズ

  cp5.addSlider("arm2_length") //アーム2用の長さを決めるスライダー（以下略）
    .setRange(10, 200)
    .setValue(100)
    .setPosition(200, 330)
    .setSize(70, 20);
}

void draw() {

  noCursor(); //カーソル矢印を表示しない
  background(128); //背景はグレー

  float x0 = width/2;// 画面の中心をx=0とした時の原点
  float y0 = height/2;// 画面の中心をy=0とした時の原点
  float x = mouseX-x0; // 画面の中心を0とした時のマウスのx座標
  float y = mouseY-y0;// 画面の中心を0とした時のマウスのy座標

  // アームが届く範囲をグレーの円で表示
  stroke(200); // 線の色はグレー
  strokeWeight(1); // 線の太さは1
  fill(150); // 円を少し濃いグレーで塗る
  ellipse(x0, y0, 2*abs(arm1_length+arm2_length), 2*abs(arm1_length+arm2_length)); //アームの最大距離の円を描く
  fill(128);// 円を背景同色のグレーで塗る
  ellipse(x0, y0, 2*abs(arm1_length-arm2_length), 2*abs(arm1_length-arm2_length)); //アームの最小距離の円を描く

  // アームが目標とする点を赤で表示
  stroke(255, 0, 0); //線の色はレッド
  strokeWeight(5); //線の太さは5
  rect( mouseX-5, mouseY-5, 11, 11 ); //マウス座標を中心に四角を描く

  //アーム1の計算
  float acos1 = sq(x)+sq(y)+sq(arm1_length)-sq(arm2_length); //逆運動学のacos分子を計算
  float acos2 = 2*arm1_length*sqrt(sq(x)+sq(y));//逆運動学のacos分母を計算
  
  //アーム1の角度を逆運動学で算出
  if (mouseX >= x0) { //atanの範囲が-π/2〜π/2 なので場合分けして計算
    arm1_angle = acos(acos1/acos2)+atan(y/x);//  アーム1の角度を求める式
  } else {
    arm1_angle = acos(acos1/acos2)+atan(y/x)+PI; // xがマイナスになる領域では180度を追加 するとうまくいく
  }

  //アーム1の線を描画。
  stroke(0, 0, 255); //アーム1はブルー
  strokeWeight(3); //線の太さは3
  //逆運動学で導いた角度をもとにアーム1の末端座標を求め、原点座標と結ぶ事で描画。
  line(x0,y0,x0+arm1_length*cos(arm1_angle), y0+arm1_length*sin(arm1_angle)); 

  //アーム2の計算
  float acos3 = sq(arm1_length)+sq(arm2_length)-(sq(x)+sq(y)); //逆運動学のacos分子を計算
  float acos4 = 2*arm1_length*arm2_length; //逆運動学のacos分母を計算
  float x2 = x0+arm1_length*cos(arm1_angle); //アーム1の終点座標をアーム2の原点とする
  float y2 = y0+arm1_length*sin(arm1_angle); //アーム1の終点座標をアーム2の原点とする
  arm2_angle = PI+acos(acos3/acos4);// アーム2の角度を逆運動学で算出
  
 //アーム2の線を描画。
  stroke(0, 255, 0); //アーム2はグリーン
 //逆運動学で導いた角度をもとにアーム2の末端の座標を求め、アーム1の末端座標と結ぶ事で描画。
  line(x2, y2, x2+ arm2_length*cos(arm1_angle+arm2_angle), y2+ arm2_length*sin(arm1_angle+arm2_angle)); 

//数値のモニタリング
  println("(", x, ",", y, ")"); //原点からのマウス座標を表示
  println("arm1_length:", arm1_length);//アーム1の長さを表示
  println("arm1_angle:", arm1_angle);//逆運動学で算出したアーム1の角度をラジアンで表示
  println("arm2_length:", arm2_length);//アーム2の長さをモニタ表示
  println("arm2_angle:", arm2_angle);//逆運動学で算出したアーム2の角度をラジアンで表示
  delay(10);
}

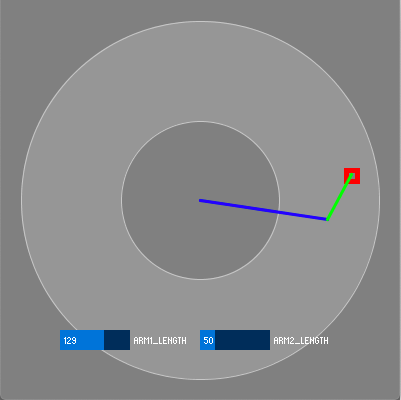
##実行例

マウスポインタの位置が赤い点で表示されます。
アームが届く範囲にマウスポインタが入ると青と緑のアームが描画されます。
下の青いスライダーでアームの長さを変更することができます。

##あとがき
atan2 を使うともっと簡単そうですが、理解を深めるためにまずは正攻法で解いてみました。
単純な構造のヒューマノイドであれば余弦定理だけでも動かせそうな感じがします。