CNNは、画像認識に用いられます。MNISTも画像ですので、CNNを適用することにより、大幅な精度向上が期待できます。CNNの実装について考えてみましょう。
ここでは、CNN自体の詳細な説明は行いませんので、詳しく知りたい方は、他で確認してください。
実装は、「ディープラーニングを実装から学ぶ(8)実装変更」をベースに行います。データは、MNISTを利用します。
畳み込み
畳み込みは、画像に対して、フィルタを動かしながら画像のデータとフィルタを掛けた和をとります。
たとえば、画像$ u $とフィルタ$ f $の畳み込みを行うと、以下のような結果となります。
\begin{align}
u &=
\begin{pmatrix}
u_{11} & u_{12} & u_{13} \\
u_{21} & u_{22} & u_{23} \\
u_{31} & u_{32} & u_{33}
\end{pmatrix}
\\
\\
f &=
\begin{pmatrix}
w_{11} & w_{12} \\
w_{21} & w_{22}
\end{pmatrix}
\\
\\
z &=
\begin{pmatrix}
u_{11}w_{11}+u_{12}w_{12}+u_{21}w_{21}+u_{22}w_{22} & u_{12}w_{11}+u_{13}w_{12}+u_{22}w_{21}+u_{23}w_{22} \\
u_{21}w_{11}+u_{22}w_{12}+u_{31}w_{21}+u_{32}w_{22} & u_{22}w_{11}+u_{23}w_{12}+u_{32}w_{21}+u_{33}w_{22}
\end{pmatrix}
\end{align}
数式で表すと以下です。
z_{ij} = \sum_{k,l=0}^{2}u_{i+k,j+l}w_{kl}
畳み込みの実装
一度に全部を実装するのは難しいため、1ステップごとに考えます。
フィルタ
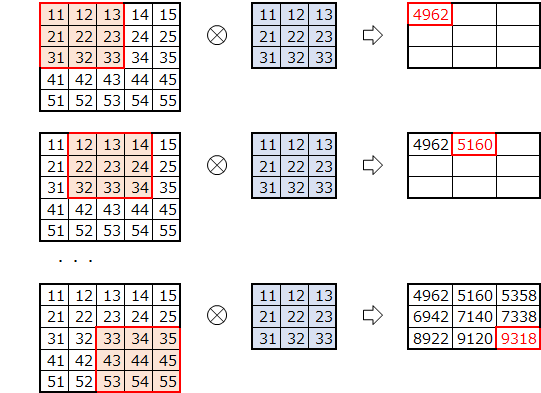
画像サイズが$ 5\times5 $、フィルタサイズが$ 3\times3 $の場合を考えます。
このように、フィルタをひとつづつ、ずらしながら掛けて和をとります。
実装
畳み込み後のサイズを考えます。
画像$ u $の高さと幅を$ uh, uw $、フィルタ$ f $の高さ、幅を$ fh, fw $とします。
畳み込み後の高さ($ zh $)、幅($ zw $)は、以下となります。
元のサイズより、フィルタ-1個分、小さくなります。
- 畳み込み後のサイズ
zh = uh-fh+1\\
zw = uw-fw+1
畳み込みのプログラムを考えます。
画像の左上から順に、ひとつずつずらしながらフィルタサイズ分切り出します。
切り出した画像とフィルタの内積を計算します。
2次元のままでは、内積を計算できないため、flattenで1次元に変換しています。
プログラムです。
def conv(u, f):
# 画像の高さ、幅
uh, uw = u.shape
# フィルタの高さ、幅
fh, fw = f.shape
# 畳み込み後の高さ、幅
zh, zw = uh-fh+1, uw-fw+1
# 畳み込み後の格納領域確保
z = np.zeros((zh, zw))
# 畳み込み後の高さ、幅分ループ
for i in range(zh):
for j in range(zw):
# 画像からフィルタサイズ分切り出し
ud = u[i:i+fh,j:j+fw]
# 切り出した画像とフィルタの内積の計算
z[i,j] = np.dot(ud.flatten(),f.flatten())
return z
実行例
先ほどの例で確認します。
import numpy as np
u55 = np.array([[11,12,13,14,15],[21,22,23,24,25],[31,32,33,34,35],[41,42,43,44,45],[51,52,53,54,55]])
f33 = np.array([[11,12,13],[21,22,23],[31,32,33]])
print("u55.shape=", u55.shape)
print("f33.shape=", f33.shape)
print("u55=")
print(u55)
print("f33=")
print(f33)
u55.shape= (5, 5)
f33.shape= (3, 3)
u55=
[[11 12 13 14 15]
[21 22 23 24 25]
[31 32 33 34 35]
[41 42 43 44 45]
[51 52 53 54 55]]
f33=
[[11 12 13]
[21 22 23]
[31 32 33]]
conv(u55, f33)
array([[ 4962., 5160., 5358.],
[ 6942., 7140., 7338.],
[ 8922., 9120., 9318.]])
パディング
畳み込みを行うと元の画像サイズより小さくなります。画像の周りにパディングを行い、畳み込み後も元の画像の大きさを維持できるようにします。通常は、0で埋めるゼロパディングを行います。
ここでは、ゼロパディングのみ対応します。
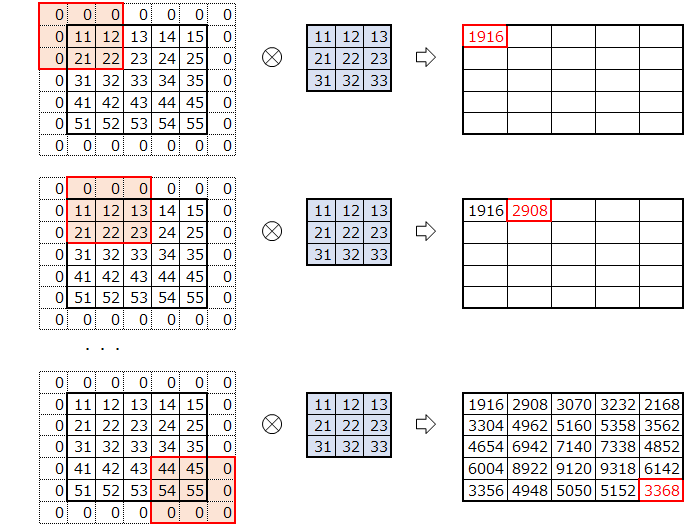
パディングサイズ1の場合は、$ pu $のようになります。
パディング後、畳み込みを実行します。
この場合は、畳み込み、前後で高さ、幅は同じになりました。
実装
パディングサイズが1の場合、パディング後の画像サイズは、左右、上下にパディングを行うため、高さ、幅とも+2となります。画像サイズがパディングによって増加した分、パディング後のサイズも大きくなります。
パディングの幅、高さを$ ph,pw $とし、画像のパディング後の高さ、幅を$ puh,puw $とします。
- パディング後のサイズ
puh = uh+2*ph\\
puw = uw+2*pw
畳み込み後のサイズは、パディング後の画像サイズより、以下となります。
- 畳み込み後のサイズ
zh = puh-fh+1\\
zw = puw-fw+1
パディング対応のプログラムです。元の画像にパディングを施した上で、畳み込みを実行しています。
def convp(u, f, p=(0,0)):
# 画像の高さ、幅
uh, uw = u.shape
# フィルタの高さ、幅
fh, fw = f.shape
# パディングの高さ、幅
ph, pw = p
# パディング後のデータ
puh, puw = uh+2*ph,uw+2*pw
pu = np.zeros((puh,puw))
pu[ph:ph+uh,pw:pw+uw] = u
# 畳み込み後の高さ、幅
zh, zw = puh-fh+1, puw-fw+1
# 畳み込み後の格納領域確保
z = np.zeros((zh, zw))
# 畳み込み後の高さ、幅分ループ
for i in range(zh):
for j in range(zw):
# 画像からフィルタサイズ分切り出し
ud = pu[i:i+fh,j:j+fw]
# 切り出した画像とフィルタの内積の計算
z[i,j] = np.dot(ud.flatten(),f.flatten())
return z
実行例
先ほどのデータにパディングサイズ=1で実行します。
convp(u55, f33, p=(1,1))
array([[ 1916., 2908., 3070., 3232., 2168.],
[ 3304., 4962., 5160., 5358., 3562.],
[ 4654., 6942., 7140., 7338., 4852.],
[ 6004., 8922., 9120., 9318., 6142.],
[ 3356., 4948., 5050., 5152., 3368.]])
畳み込み後も元のサイズと同じになりました。
ストライド
今までは、フィルタを1ずつずらしていました。フィルタをずらす幅を指定してみます。
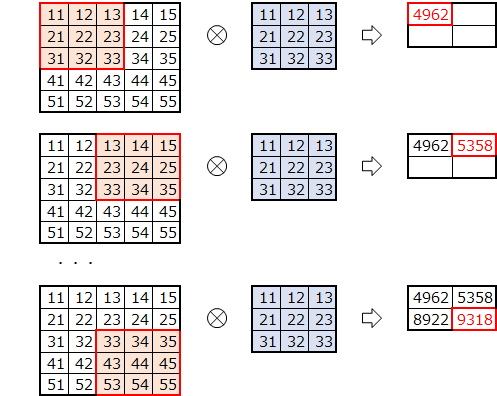
ストライドを2とし、2つずつずらしてみます。
実装
畳み込み後のサイズを考えます。
ストライドずつ移動するため、ストライドで割ります。
画像のパディング後の高さ、幅を$ puh,puw$、ストライドの高さ、幅を$ sh,sw $とします。
- 畳み込み後のサイズ
zh = (puh-fh)/sh+1\\
zw = (puw-fw)/sw+1
プログラムです。畳み込みをストライド分ずらして実行していきます。
def convps(u, f, p=(0,0), s=(1,1)):
# 画像の高さ、幅
uh, uw = u.shape
# フィルタの高さ、幅
fh, fw = f.shape
# パディングの高さ、幅
ph, pw = p
# ストライドの高さ、幅
sh, sw = s
# パディング後のデータ
puh, puw = uh+2*ph,uw+2*pw
pu = np.zeros((puh,puw))
pu[ph:ph+uh,pw:pw+uw] = u
# 畳み込み後の高さ、幅
zh, zw = int((puh-fh)/sh)+1, int((puw-fw)/sw)+1
# 畳み込み後の格納領域確保
z = np.zeros((zh, zw))
# 畳み込み後の高さ、幅分ループ
for i in range(zh):
for j in range(zw):
# 画像からフィルタサイズ分切り出し
ud = pu[i*sh:i*sh+fh,j*sw:j*sw+fw]
# 切り出した画像とフィルタの内積の計算
z[i,j] = np.dot(ud.flatten(),f.flatten())
return z
実行例
先ほどのデータにストライド=2で実行します
convps(u55, f33, s=(2,2))
array([[ 4962., 5358.],
[ 8922., 9318.]])
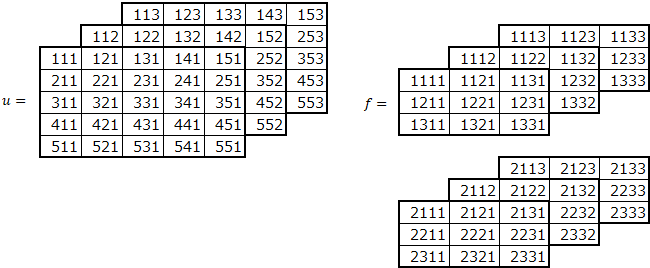
チャネル
MNISTは、単色のため2次元のデータでした。カラー画像では、RGBの色のデータを加えて3次元となります。カラー画像への対応を考えます。
フィルタもチャネルを加えて、3次元となります。画像とフィルタのチャネル数は同じにします。
色を1次元目にするか3次元目にするか、両方のデータが存在するようですが、ここでは、色のデータは、3次元目とします。
画像、フィルタの各次元は、以下を表します。
(高さ、幅、チャネル)
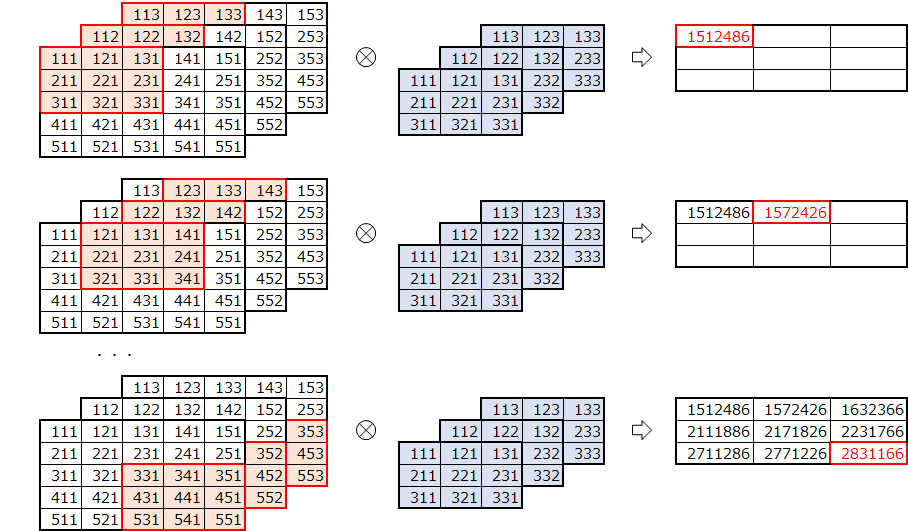
畳み込みを行います。
各チャネルごとに、画像をフィルタサイズ分抽出し、各フィルタと掛けてすべてのチャネル分足し合わせます。
実装
基本的に、3次元目にチャネルが増えただけです。
def convpsc(u, f, p=(0,0), s=(1,1)):
# 画像の高さ、幅、チャネル
uh, uw, uc = u.shape
# フィルタの高さ、幅、チャネル
fh, fw, fc = f.shape
# パディングの高さ、幅
ph, pw = p
# ストライドの高さ、幅
sh, sw = s
# パディング後のデータ
puh, puw = uh+2*ph,uw+2*pw
pu = np.zeros((puh,puw,uc))
pu[ph:ph+uh,pw:pw+uw,:] = u
# 畳み込み後の高さ、幅
zh, zw = int((puh-fh)/sh)+1, int((puw-fw)/sw)+1
# 畳み込み後の格納領域確保
z = np.zeros((zh, zw))
# 畳み込み後の高さ、幅分ループ
for i in range(zh):
for j in range(zw):
# 画像からフィルタサイズ分切り出し
ud = pu[i*sh:i*sh+fh,j*sw:j*sw+fw,:]
# 切り出した画像とフィルタの内積の計算
z[i,j] = np.dot(ud.flatten(),f.flatten())
return z
実行例
チャネルを3としたデータ例です。
import numpy as np
u553 = np.array([[[111,112,113],[121,122,123],[131,132,133],[141,142,143],[151,152,153]],
[[211,212,213],[221,222,223],[231,232,233],[241,242,243],[251,252,253]],
[[311,312,313],[321,322,323],[331,332,333],[341,342,343],[351,352,353]],
[[411,412,413],[421,422,423],[431,432,433],[441,442,443],[451,452,453]],
[[511,512,513],[521,522,523],[531,532,533],[541,542,543],[551,552,553]]])
f333 = np.array([[[111,112,113],[121,122,123],[131,132,133]],
[[211,212,213],[221,222,223],[231,232,233]],
[[311,312,313],[321,322,323],[331,332,333]]])
print("u553.shape=", u553.shape)
print("f333.shape=", f333.shape)
print("u553=")
for i in range(3):
print(u553[:,:,i])
print("f333=")
for i in range(3):
print(f333[:,:,i])
u553.shape= (5, 5, 3)
f333.shape= (3, 3, 3)
u553=
[[111 121 131 141 151]
[211 221 231 241 251]
[311 321 331 341 351]
[411 421 431 441 451]
[511 521 531 541 551]]
[[112 122 132 142 152]
[212 222 232 242 252]
[312 322 332 342 352]
[412 422 432 442 452]
[512 522 532 542 552]]
[[113 123 133 143 153]
[213 223 233 243 253]
[313 323 333 343 353]
[413 423 433 443 453]
[513 523 533 543 553]]
f333=
[[111 121 131]
[211 221 231]
[311 321 331]]
[[112 122 132]
[212 222 232]
[312 322 332]]
[[113 123 133]
[213 223 233]
[313 323 333]]
畳み込みの実行
convpsc(u553, f333)
array([[ 1512486., 1572426., 1632366.],
[ 2111886., 2171826., 2231766.],
[ 2711286., 2771226., 2831166.]])
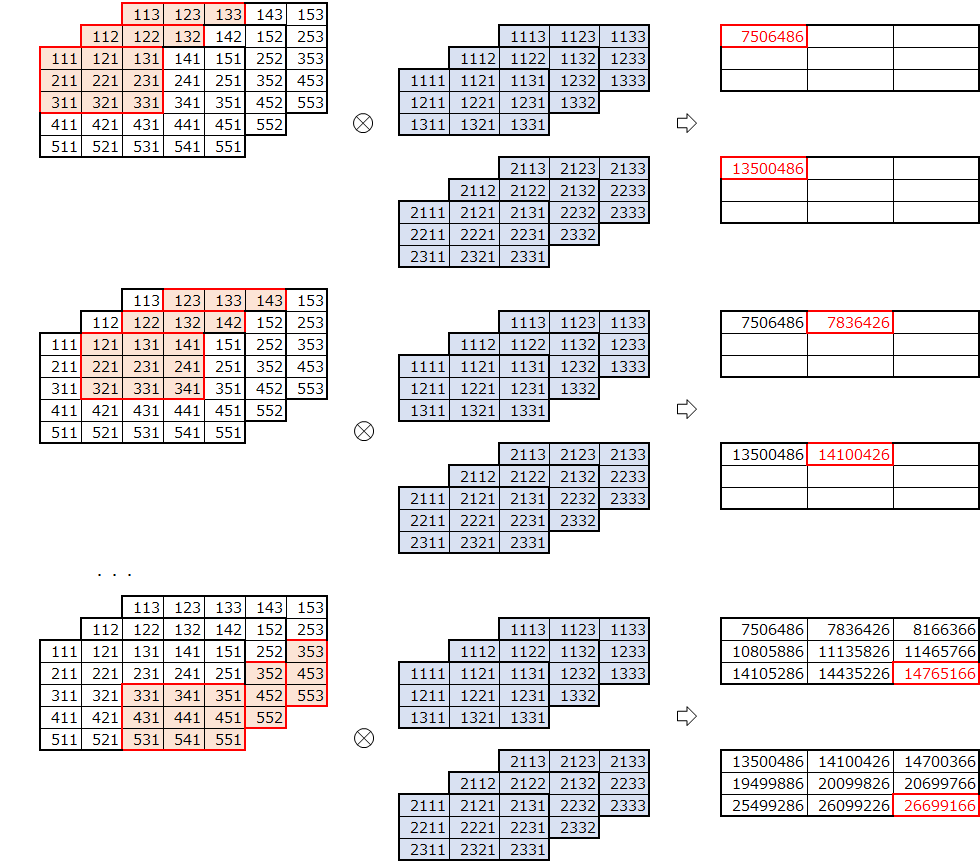
フィルタ数
今度は、フィルタ数を複数にしてみます。フィルターは、以下の4次元となります。
(フィルタ、高さ、幅、チャネル)
フィルタ数2の例です。
フィルタごとに畳み込みを行います。
畳み込み後は、フィルタ数分のデータとなり、3次元になります。
実装
基本は、同じですが、内積の部分に注意が必要です。
フィルタのひとつひとつと内積をとるため、フィルタをreshapeしています。その後、内積を行えるように転置します。
def convpscf(u, f, p=(0,0), s=(1,1)):
# 画像の高さ、幅、チャネル
uh, uw, uc = u.shape
# フィルタの数、高さ、幅、チャネル
fn, fh, fw, fc = f.shape
# パディングの高さ、幅
ph, pw = p
# ストライドの高さ、幅
sh, sw = s
# パディング後のデータ
puh, puw = uh+2*ph,uw+2*pw
pu = np.zeros((puh,puw,uc))
pu[ph:ph+uh,pw:pw+uw,:] = u
# 畳み込み後の高さ、幅
zh, zw = int((puh-fh)/sh)+1, int((puw-fw)/sw)+1
# 畳み込み後の格納領域確保
z = np.zeros((zh, zw, fn))
# 畳み込み後の高さ、幅分ループ
for i in range(zh):
for j in range(zw):
# 画像からフィルタサイズ分切り出し
ud = pu[i*sh:i*sh+fh,j*sw:j*sw+fw,:]
# 切り出した画像とフィルタの内積の計算
z[i,j,:] = np.dot(ud.flatten(),f.reshape((fn,fh*fw*fc)).T)
return z
実行例
フィルタ数を2とした場合の例です。
import numpy as np
f2333 = np.array([[[[1111,1112,1113],[1121,1122,1123],[1131,1132,1133]],
[[1211,1212,1213],[1221,1222,1223],[1231,1232,1233]],
[[1311,1312,1313],[1321,1322,1323],[1331,1332,1333]]],
[[[2111,2112,2113],[2121,2122,2123],[2131,2132,2133]],
[[2211,2212,2213],[2221,2222,2223],[2231,2232,2233]],
[[2311,2312,2313],[2321,2322,2323],[2331,2332,2333]]]])
print("f2333.shape=", f2333.shape)
print("f2333=")
for i in range(2):
for j in range(3):
print(f2333[i,:,:,j])
f2333.shape= (2, 3, 3, 3)
f2333=
[[1111 1121 1131]
[1211 1221 1231]
[1311 1321 1331]]
[[1112 1122 1132]
[1212 1222 1232]
[1312 1322 1332]]
[[1113 1123 1133]
[1213 1223 1233]
[1313 1323 1333]]
[[2111 2121 2131]
[2211 2221 2231]
[2311 2321 2331]]
[[2112 2122 2132]
[2212 2222 2232]
[2312 2322 2332]]
[[2113 2123 2133]
[2213 2223 2233]
[2313 2323 2333]]
畳み込みの実行
z = convpscf(u553, f2333)
print("z=")
for i in range(2):
print(z[:,:,i])
z=
[[ 7506486. 7836426. 8166366.]
[ 10805886. 11135826. 11465766.]
[ 14105286. 14435226. 14765166.]]
[[ 13500486. 14100426. 14700366.]
[ 19499886. 20099826. 20699766.]
[ 25499286. 26099226. 26699166.]]
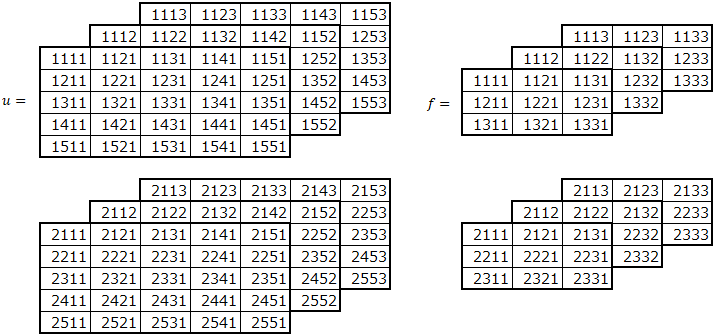
データ数
最後に、データを複数にしてみます。バッチサイズ分のデータを一度に畳み込みする必要があります。
データは、以下の4次元となります。
(データ、高さ、幅、チャネル)
データ数2の例です。
畳み込みを行います。
畳み込みは、各データとフィルターの組み合わせで行います。
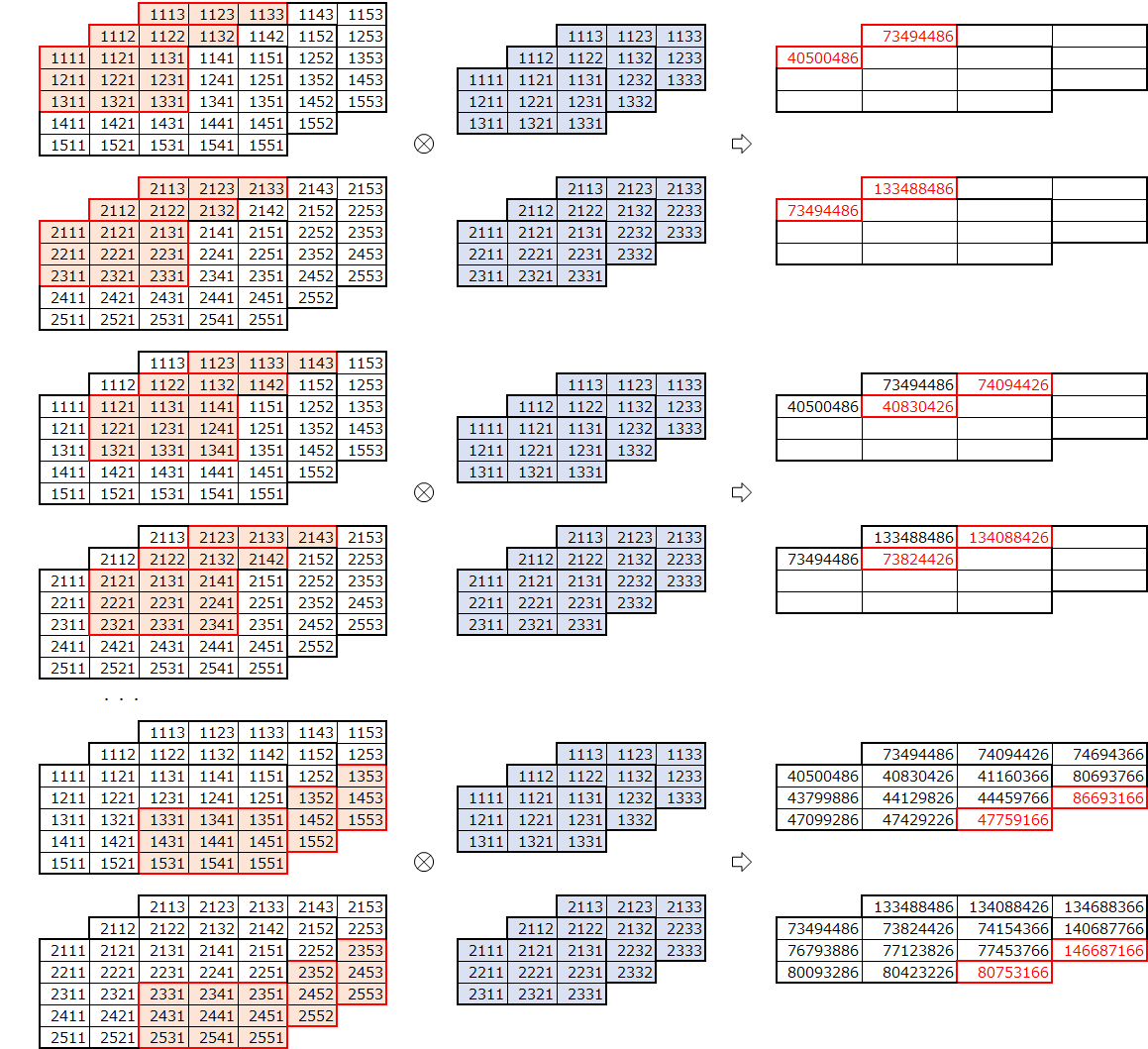
実装
フィルター数の対応を行った場合と同様に、内積の部分に注意が必要です。
データのひとつひとつと内積をとるため、データをフィルターと内積が取れるようにreshapeしています。
def convpscfu(u, f, p=(0,0), s=(1,1)):
# 画像の数、高さ、幅、チャネル
un, uh, uw, uc = u.shape
# フィルタの数、高さ、幅、チャネル
fn, fh, fw, fc = f.shape
# パディングの高さ、幅
ph, pw = p
# ストライドの高さ、幅
sh, sw = s
# パディング後のデータ
puh, puw = uh+2*ph,uw+2*pw
pu = np.zeros((un,puh,puw,uc))
pu[:,ph:ph+uh,pw:pw+uw,:] = u
# 畳み込み後の高さ、幅
zh, zw = int((puh-fh)/sh)+1, int((puw-fw)/sw)+1
# 畳み込み後の格納領域確保
z = np.zeros((un, zh, zw, fn))
# 畳み込み後の高さ、幅分ループ
for i in range(zh):
for j in range(zw):
# 画像からフィルタサイズ分切り出し
ud = pu[:,i*sh:i*sh+fh,j*sw:j*sw+fw,:]
# 切り出した画像とフィルタの内積の計算
z[:,i,j,:] = np.dot(ud.reshape((un,fh*fw*uc)),f.reshape((fn,fh*fw*fc)).T)
return z
実行例
データ数を2とした場合の例です。
import numpy as np
u2553 = np.array([[[[1111,1112,1113],[1121,1122,1123],[1131,1132,1133],[1141,1142,1143],[1151,1152,1153]],
[[1211,1212,1213],[1221,1222,1223],[1231,1232,1233],[1241,1242,1243],[1251,1252,1253]],
[[1311,1312,1313],[1321,1322,1323],[1331,1332,1333],[1341,1342,1343],[1351,1352,1353]],
[[1411,1412,1413],[1421,1422,1423],[1431,1432,1433],[1441,1442,1443],[1451,1452,1453]],
[[1511,1512,1513],[1521,1522,1523],[1531,1532,1533],[1541,1542,1543],[1551,1552,1553]]],
[[[2111,2112,2113],[2121,2122,2123],[2131,2132,2133],[2141,2142,2143],[2151,2152,2153]],
[[2211,2212,2213],[2221,2222,2223],[2231,2232,2233],[2241,2242,2243],[2251,2252,2253]],
[[2311,2312,2313],[2321,2322,2323],[2331,2332,2333],[2341,2342,2343],[2351,2352,2353]],
[[2411,2412,2413],[2421,2422,2423],[2431,2432,2433],[2441,2442,2443],[2451,2452,2453]],
[[2511,2512,2513],[2521,2522,2523],[2531,2532,2533],[2541,2542,2543],[2551,2552,2553]]]])
print("u2553.shape=", u2553.shape)
print("u2553=")
for i in range(2):
for j in range(3):
print(u2553[i,:,:,j])
u2553.shape= (2, 5, 5, 3)
u2553=
[[1111 1121 1131 1141 1151]
[1211 1221 1231 1241 1251]
[1311 1321 1331 1341 1351]
[1411 1421 1431 1441 1451]
[1511 1521 1531 1541 1551]]
[[1112 1122 1132 1142 1152]
[1212 1222 1232 1242 1252]
[1312 1322 1332 1342 1352]
[1412 1422 1432 1442 1452]
[1512 1522 1532 1542 1552]]
[[1113 1123 1133 1143 1153]
[1213 1223 1233 1243 1253]
[1313 1323 1333 1343 1353]
[1413 1423 1433 1443 1453]
[1513 1523 1533 1543 1553]]
[[2111 2121 2131 2141 2151]
[2211 2221 2231 2241 2251]
[2311 2321 2331 2341 2351]
[2411 2421 2431 2441 2451]
[2511 2521 2531 2541 2551]]
[[2112 2122 2132 2142 2152]
[2212 2222 2232 2242 2252]
[2312 2322 2332 2342 2352]
[2412 2422 2432 2442 2452]
[2512 2522 2532 2542 2552]]
[[2113 2123 2133 2143 2153]
[2213 2223 2233 2243 2253]
[2313 2323 2333 2343 2353]
[2413 2423 2433 2443 2453]
[2513 2523 2533 2543 2553]]
畳み込みの実行
z = convpscfu(u2553, f2333)
for i in range(2):
print("z[",i,"]=")
for j in range(2):
print(z[i,:,:,j])
z[ 0 ]=
[[ 40500486. 40830426. 41160366.]
[ 43799886. 44129826. 44459766.]
[ 47099286. 47429226. 47759166.]]
[[ 73494486. 74094426. 74694366.]
[ 79493886. 80093826. 80693766.]
[ 85493286. 86093226. 86693166.]]
z[ 1 ]=
[[ 73494486. 73824426. 74154366.]
[ 76793886. 77123826. 77453766.]
[ 80093286. 80423226. 80753166.]]
[[ 1.33488486e+08 1.34088426e+08 1.34688366e+08]
[ 1.39487886e+08 1.40087826e+08 1.40687766e+08]
[ 1.45487286e+08 1.46087226e+08 1.46687166e+08]]
データの値は、分かりやすくするため、データの添え字にしましたが、大きな値になり、指数表現になってしまいました。分かりやすくしたつもりが、分かりにくくなっていますね。
順伝播
最終的に4次元の配列どうしの演算となるため、混乱しないように、ひとつひとつ次元を増やしながら確認しました。
ここからは、正式な対応を行います。
今までは、バイアスを考慮していませんでした。バイアスを追加します。バイアスは、フィルタごとに1つです。
\begin{align}
u &=
\begin{pmatrix}
u_{11} & u_{12} & u_{13} \\
u_{21} & u_{22} & u_{23} \\
u_{31} & u_{32} & u_{33}
\end{pmatrix}
\\
\\
f &=
\begin{pmatrix}
w_{11} & w_{12} \\
w_{21} & w_{22}
\end{pmatrix}
\\
\\
z &=
\begin{pmatrix}
u_{11}w_{11}+u_{12}w_{12}+u_{21}w_{21}+u_{22}w_{22}+b & u_{12}w_{11}+u_{13}w_{12}+u_{22}w_{21}+u_{23}w_{22}+b \\
u_{21}w_{11}+u_{22}w_{12}+u_{31}w_{21}+u_{32}w_{22}+b & u_{22}w_{11}+u_{23}w_{12}+u_{32}w_{21}+u_{33}w_{22}+b
\end{pmatrix}
\end{align}
実装
パディングとストライドは、整数を設定すれば、高さ、幅に同じ値を設定されるように変更しました。高さ、幅の値を変えたい場合は、高さ、幅をタプルで指定します。
def convolution2d(u, W, b, padding=0, strides=1):
# パディング
if type(padding) == int:
padding_h, padding_w = padding, padding
else:
padding_h, padding_w = padding
# ストライド
if type(strides) == int:
strides_h, strides_w = strides, strides
else:
strides_h, strides_w = strides
# 画像の数、高さ、幅、チャネル
un, uh, uw, uc = u.shape
# フィルタの数、高さ、幅、チャネル
fn, fh, fw, fc = W.shape
# パディング後の高さ、幅
ph, pw = uh + padding_h*2, uw + padding_w*2
# パディング
pu = np.zeros((un, ph, pw, uc))
pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u
# 畳み込み後の高さ、幅
zh, zw = int((ph-fh)/strides_h)+1, int((pw-fw)/strides_w)+1
# 畳み込み後の格納領域確保
z = np.zeros((un, zh, zw, fn))
# 畳み込み後の高さ、幅分ループ
for i in range(zh):
for j in range(zw):
# 画像からフィルタサイズ分切り出し
# ud - (un, fh, fw, uc)
ud = pu[:, i*strides_h:i*strides_h+fh, j*strides_w:j*strides_w+fw, :]
# 切り出した画像とフィルタの内積の計算
# (un, fh*fw*fc) @ (fh*fw*fx, fn) => (un, fn)
z[:, i, j, :] = np.dot(ud.reshape(un, fh*fw*fc), W.reshape(fn, fh*fw*fc).T) + b
return z
逆伝播
順伝播は、以下のように計算しました。
\begin{align}
u &=
\begin{pmatrix}
u_{11} & u_{12} & u_{13} \\
u_{21} & u_{22} & u_{23} \\
u_{31} & u_{32} & u_{33}
\end{pmatrix}
\\
\\
f &=
\begin{pmatrix}
w_{11} & w_{12} \\
w_{21} & w_{22}
\end{pmatrix}
\\
\\
z &=
\begin{pmatrix}
u_{11}w_{11}+u_{12}w_{12}+u_{21}w_{21}+u_{22}w_{22} & u_{12}w_{11}+u_{13}w_{12}+u_{22}w_{21}+u_{23}w_{22} \\
u_{21}w_{11}+u_{22}w_{12}+u_{31}w_{21}+u_{32}w_{22} & u_{22}w_{11}+u_{23}w_{12}+u_{32}w_{21}+u_{33}w_{22}
\end{pmatrix}
\end{align}
後ろからの勾配は、以下とします。
dz =
\begin{pmatrix}
dz_{11} & dz_{12} \\
dz_{21} & dz_{22}
\end{pmatrix}
$ z_{11} $について、勾配を考えます。
z_{11} = u_{11}w_{11}+u_{12}w_{12}+u_{21}w_{21}+u_{22}w_{22}+b
$ u_{11} $方向
{\frac{\partial z_{11}}{\partial u_{11}} = w_{11}}
後ろからの勾配$ dz_{11} $を掛けた値$ w_{11}dz_{11} $が勾配になります。
$ w_{11} $方向
{\frac{\partial z_{11}}{\partial w_{11}} = u_{11}}
後ろからの勾配$ dz_{11} $を掛けた値$ u_{11}dz_{11} $が勾配になります。
$ b $方向
{\frac{\partial z_{11}}{\partial b} = 1}
後ろからの勾配$ dz_{11} $を掛けた値$ dz_{11} $が勾配になります。
全体の勾配を考えます。
- $ u $の勾配$ du $
まずは、$ dz_{11} $についてです。$ z_{11} $に関係する場所に影響します。
\begin{pmatrix}
w_{11}dz_{11} & w_{12}dz_{11} & 0 \\
w_{21}dz_{11} & w_{22}dz_{11} & 0 \\
0 & 0 & 0
\end{pmatrix}
次に、$ dz_{12} $についてです。
\begin{pmatrix}
0 & w_{11}dz_{12} & w_{12}dz_{12} \\
0 & w_{21}dz_{12} & w_{22}dz_{12} \\
0 & 0 & 0
\end{pmatrix}
$ f $と各$ dz $の内積をとり、もとの位置に戻します。
最終的には、同じ場所は加え以下となります。
\begin{pmatrix}
w_{11}dz_{11} & w_{12}dz_{11}+w_{11}dz_{12} & w_{12}dz_{12} \\
w_{21}dz_{11}+w_{11}dz_{21} & w_{22}dz_{11}+w_{21}dz_{12}+w_{12}dz_{21}+w_{11}dz_{22} & w_{22}dz_{12}+w_{12}dz_{22} \\
w_{21}dz_{21} & w_{22}dz_{21}+w_{21}dz_{22} & w_{22}dz_{22}
\end{pmatrix}
- $ w $の勾配$ dw $
まずは、$ dz_{11} $についてです。$ z_{11} $に関係する場所に影響します。
\begin{pmatrix}
u_{11}dz_{11} & u_{12}dz_{11} \\
u_{21}dz_{11} & u_{22}dz_{11}
\end{pmatrix}
次に、$ dz_{12} $についてです。
\begin{pmatrix}
u_{12}dz_{12} & u_{13}dz_{12} \\
u_{22}dz_{12} & u_{23}dz_{12}
\end{pmatrix}
$ z $のもとになった$ u $と$ dz $の内積となります。
最終的には、それぞれ加え以下となります。
\begin{pmatrix}
u_{11}dz_{11}+u_{12}dz_{12}+u_{21}dz_{21}+u_{22}dz_{22} & u_{12}dz_{11}+u_{13}dz_{12}+u_{22}dz_{21}+u_{23}dz_{22} \\
u_{21}dz_{11}+u_{22}dz_{12}+u_{31}dz_{21}+u_{32}dz_{22} & u_{22}dz_{11}+u_{23}dz_{12}+u_{32}dz_{21}+u_{33}dz_{22}
\end{pmatrix}
- $ b $の勾配$ db $
$ dz_{11} $は、$ b $方向の勾配が1のため、そのままの値です。
$ 1 \times dz_{11} = dz_{11} $
最終的には、すべて足した値となります。
dz_{11} + dz_{12} + dz_{21} + dz_{22}
実装
勾配は、単純な2次元で説明しましたが、4次元となっても同様です。内積を行うためreshapeが必要です。
def convolution2d_back(dz, u, W, b, padding=0, strides=1):
# パディング
if type(padding) == int:
padding_h, padding_w = padding, padding
else:
padding_h, padding_w = padding
# ストライド
if type(strides) == int:
strides_h, strides_w = strides, strides
else:
strides_h, strides_w = strides
# 画像の数、高さ、幅、チャネル
un, uh, uw, uc = u.shape
# フィルターの数、高さ、幅、チャネル
fn, fh, fw, fc = W.shape
# パディング後の高さ、幅
ph, pw = uh + padding_h*2, uw + padding_w*2
# パディング
pu = np.zeros((un, ph, pw, uc))
pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u
# 畳み込み後の高さ、幅
zh, zw = int((ph-fh)/strides_h)+1, int((pw-fw)/strides_w)+1
# 勾配格納領域確保
dpu = np.zeros((un, ph, pw, uc))
dW = np.zeros((fn, fh, fw, fc))
# 畳み込み後の高さ、幅分ループ
for i in range(zh):
for j in range(zw):
# dzijの取り出し
# dzs - (un, fn)
dzs = dz[:,i,j,:]
# u方向の勾配計算
# dpusr - (un,fn) @ (fn, fh*fw*fc) => (un, fh*fw*fc)
dpusr = np.dot(dzs, W.reshape(fn, fh*fw*fc))
# dpus - (un, fh, fw, uc)
dpus = dpusr.reshape(un, fh, fw, uc)
dpu[:, i*strides_h:i*strides_h+fh, j*strides_w:j*strides_w+fw, :] += dpus
# W方向の勾配計算
# pus - (un, fh*fw*uc)
pus = pu[:, i*strides_h:i*strides_h+fh, j*strides_w:j*strides_w+fw, :]
# pudr - (un, fh*fw*uc)
pusr = pus.reshape(un, fh*fw*uc)
# dWsr - (fn, un) @ (un, fh*fw*uc) => (fn, fh*fw*uc)
dWsr = np.dot(dzs.T, pusr)
# dWs - (fn, fh, fw, fc=uc)
dWs = dWsr.reshape(fn, fh, fw, fc)
dW = dW + dWs
# パディング部分の除去
du = dpu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :]
# b方向の勾配計算
db = np.sum(dz.reshape(un*zh*zw, fn), axis=0)
return du, dW, db
プーリング
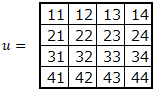
プーリング層では、画像の圧縮を行います。圧縮方式としては、一定範囲の最大値を取る、マックスプーリングが一般的に用いられます。ここは、マックスプーリングと平均を取る平均プーリングについて考えます。
マックスプーリングの実装
一定の範囲の最大値をデータとして抽出します。範囲は、プールサイズとして指定します。畳み込みと同様に、パディング、ストライドにも対応します。ストライドは、基本的にプールサイズと同じにします。すなわち、範囲が重ならないように移動しながら最大値を計算します。
プーリングは、チャネルごとに行います。プーリング後もチャネル数は変わりません。
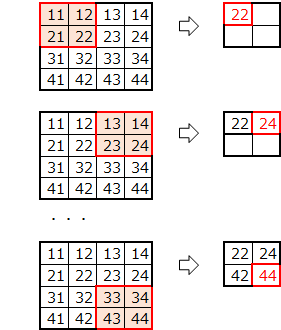
マックスプーリングの適用例です。
ここでは、プールサイズ=2分移動しながら最大値を抽出しています。
順伝播
プーリング後のサイズは、以下のように、元のサイズをプールサイズで割ったものとなります。
zh = uh/pool\_size\_h\\
zw = uw/pool\_size\_w
パディングを適用した場合のサイズです。パディング後のサイズを$ ph,pw $とすると以下のようになります。
zh = ph/pool\_size\_h\\
zw = pw/pool\_size\_w
最後にストライド適用後のサイズを考えます。今までは、プールサイズ=ストライドで考えていました。プールサイズとは別に、ストライドを設定した場合を考えます。以下のようになります。
zh = (ph-pool\_size\_h)/strides\_h + 1\\
zw = (pw-pool\_size\_w)/strides\_w + 1
実装は、基本的に畳み込みと同じですが、フィルタとの内積を取るのではなく、maxで最大値を抽出します。
def max_pooling2d(u, pool_size=2, padding=0, strides=None):
# ストライド設定
if strides is None:
strides = pool_size
# プールサイズ
if type(pool_size) == int:
pool_size_h, pool_size_w = pool_size, pool_size
else:
pool_size_h, pool_size_w = pool_size
# パディング
if type(padding) == int:
padding_h, padding_w = padding, padding
else:
padding_h, padding_w = padding
# ストライド
if type(strides) == int:
strides_h, strides_w = strides, strides
else:
strides_h, strides_w = strides
# 画像の数、高さ、幅、チャネル
un, uh, uw, uc = u.shape
# パディング後の高さ、幅
ph, pw = uh + padding_h*2, uw + padding_w*2
# パディング
pu = np.zeros((un, ph, pw, uc))
pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u
# プーリング後の高さ、幅
zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1
# プーリング後の格納領域確保
z = np.zeros((un, zh, zw, uc))
# プーリング後の高さ、幅分ループ
for i in range(zh):
for j in range(zw):
# 画像からプーリングサイズ分切り出し
# pus - (un, pool_size_h, pool_size_w, uc)
pus = pu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :]
# 切り出した画像の最大
z[:, i, j, :] = np.max(pus.reshape(un, pool_size_h*pool_size_w, uc), axis=1)
return z
逆伝播
最大の値をそのまま後ろに流しているため、逆伝播では、最大値のところに、dzの値をそのまま返します。
argmaxで最大値の位置を取得します。データごとに最大値の位置が違うので、forループで、データ数、チャネル分ひとつずつ設定しています。
def max_pooling2d_back(dz, u, z, pool_size=2, padding=0, strides=None):
# ストライド設定
if strides is None:
strides = pool_size
# プールサイズ
if type(pool_size) == int:
pool_size_h, pool_size_w = pool_size, pool_size
else:
pool_size_h, pool_size_w = pool_size
# パディング
if type(padding) == int:
padding_h, padding_w = padding, padding
else:
padding_h, padding_w = padding
# ストライド
if type(strides) == int:
strides_h, strides_w = strides, strides
else:
strides_h, strides_w = strides
# 画像の数、高さ、幅、チャネル
un, uh, uw, uc = u.shape
# パディング後の高さ、幅
ph, pw = uh + padding_h*2, uw + padding_w*2
# パディング
pu = np.zeros((un, ph, pw, uc))
pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u
# プーリング後のデータ格納用
zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1
# 勾配格納領域確保
dpu = np.zeros((un, ph, pw, uc))
# プーリング後の高さ、幅分ループ
for i in range(zh):
for j in range(zw):
# dzijの取り出し
# dzs - (un, fn)
dzs = dz[:,i,j,:]
# 最大の要素
pus = pu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :]
z_argmax = np.argmax(pus.reshape(un, pool_size_h*pool_size_w, uc), axis=1)
# 勾配格納領域確保
dusr = np.zeros((un, pool_size_h*pool_size_w, uc))
# データ数、チャネル分ループ
for k in range(un):
for l in range(uc):
# 最大の要素にdzを設定
dusr[k, z_argmax[k,l], l] = dzs[k, l]
# 勾配設定
dus = dusr.reshape(un, pool_size_h, pool_size_w, uc)
dpu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :] += dus
# パディング部分の除去
du = dpu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :]
return du
本当は、forループは使用せず、一気に設定したかったのですが、良い方法が分かりませんでした。
実際に、実行してみると、性能が遅く使いものになりませんでした。
その後、検討の結果、transposeによって、配列の順番を変えれば対応できることがわかりました。
最大値の場所への代入ですが、データとチャネル部分が離れていて、一度に代入することができませんでした。transposeにより、データ、チャネル、高さ、幅の順に並び変えることにより、データ・チャネルごとに最大の高さ・幅の位置に代入できます。代入後に、再度、transposeを行い、位置を元に戻します。
def max_pooling2d_back(dz, u, z, pool_size=2, padding=0, strides=None):
# ストライド設定
if strides is None:
strides = pool_size
# プールサイズ
if type(pool_size) == int:
pool_size_h, pool_size_w = pool_size, pool_size
else:
pool_size_h, pool_size_w = pool_size
# パディング
if type(padding) == int:
padding_h, padding_w = padding, padding
else:
padding_h, padding_w = padding
# ストライド
if type(strides) == int:
strides_h, strides_w = strides, strides
else:
strides_h, strides_w = strides
# 画像の数、高さ、幅、チャネル
un, uh, uw, uc = u.shape
# パディング後の高さ、幅
ph, pw = uh + padding_h*2, uw + padding_w*2
# パディング
pu = np.zeros((un, ph, pw, uc))
pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u
# プーリング後のデータ格納用
zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1
# 勾配格納領域確保
dpu = np.zeros((un, ph, pw, uc))
# プーリング後の高さ、幅分ループ
for i in range(zh):
for j in range(zw):
# dzijの取り出し
# dzs - (un, fn)
dzs = dz[:,i,j,:]
# 最大の要素
pus = pu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :]
# 順番並び替え
pustr = pus.transpose(0, 3, 1, 2)
# 最大の要素
z_argmax = np.argmax(pustr.reshape(un*uc, pool_size_h*pool_size_w), axis=1)
# 勾配格納
dudrtr = np.zeros((un*uc, pool_size_h*pool_size_w))
dudrtr[np.arange(un*uc), z_argmax.ravel()] = dzs.ravel()
dudtr = dudrtr.reshape(un, uc, pool_size_h, pool_size_w)
# 順番元に戻す
dud = dudtr.transpose(0, 2, 3, 1)
# 勾配設定
dpu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :] += dud
du = dpu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :]
return du
かなり性能改善できました。
平均プーリングの実装
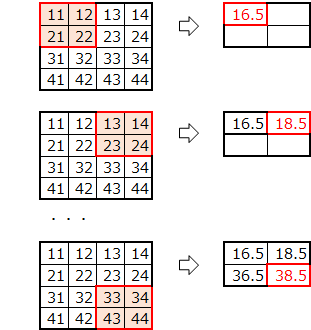
マックスプーリングは、プールサイズ分の画像から最大値を抽出していたのに対して、平均プーリングでは、平均を行います。
平均プーリングの適用例です。
ここでは、プールサイズ=2分移動しながら平均値を求めています。
順伝播
マックスプーリングとの違いは、プーリングの関数をmaxからmeanに変更するのみです。
def average_pooling2d(u, pool_size=2, padding=0, strides=None):
# ストライド設定
if strides is None:
strides = pool_size
# プールサイズ
if type(pool_size) == int:
pool_size_h, pool_size_w = pool_size, pool_size
else:
pool_size_h, pool_size_w = pool_size
# パディング
if type(padding) == int:
padding_h, padding_w = padding, padding
else:
padding_h, padding_w = padding
# ストライド
if type(strides) == int:
strides_h, strides_w = strides, strides
else:
strides_h, strides_w = strides
# 画像の数、高さ、幅、チャネル
un, uh, uw, uc = u.shape
# パディング後の高さ、幅
ph, pw = uh + padding_h*2, uw + padding_w*2
# パディング
pu = np.zeros((un, ph, pw, uc))
pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u
# プーリング後の高さ、幅
zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1
# プーリング後の格納領域確保
z = np.zeros((un, zh, zw, uc))
# プーリング後の高さ、幅分ループ
for i in range(zh):
for j in range(zw):
# 画像からプーリングサイズ分切り出し
# pus - (un, pool_size_h, pool_size_w, uc)
pus = pu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :]
# 切り出した画像の平均
z[:, i, j, :] = np.mean(pus.reshape(un, pool_size_h*pool_size_w, uc), axis=1)
return z
逆伝播
順伝播は、以下のように決定していました。
\begin{align}
u &=
\begin{pmatrix}
u_{11} & u_{12} & u_{13} & u_{14}\\
u_{21} & u_{22} & u_{23} & u_{24}\\
u_{31} & u_{32} & u_{33} & u_{34}\\
u_{41} & u_{42} & u_{43} & u_{44}
\end{pmatrix}
\\
\\
z &=
\begin{pmatrix}
\frac{u_{11}+u_{12}+u_{21}+u_{22}}{4} & \frac{u_{13}+u_{14}+u_{23}+u_{24}}{4} \\
\frac{u_{31}+u_{32}+u_{41}+u_{42}}{4} & \frac{u_{33}+u_{34}+u_{43}+u_{44}}{4}
\end{pmatrix}
\end{align}
$ z_{11} $について、勾配を考えます。
z_{11} = \frac{u_{11}+u_{12}+u_{21}+u_{22}}{4}
$ u_{11} $方向
{\frac{\partial z_{11}}{\partial u_{11}} = \frac{1}{4}}
後ろからの勾配$ dz_{11} $を掛けた値$ dz_{11}/4 $が勾配になります。
$ dz $をpool_size_h $ \times $ pool_size_wで割ります。それを、平均を求めた元の場所に加えます。
def average_pooling2d_back(dz, u, z, pool_size=2, padding=0, strides=None):
# ストライド設定
if strides is None:
strides = pool_size
# プールサイズ
if type(pool_size) == int:
pool_size_h, pool_size_w = pool_size, pool_size
else:
pool_size_h, pool_size_w = pool_size
# パディング
if type(padding) == int:
padding_h, padding_w = padding, padding
else:
padding_h, padding_w = padding
# ストライド
if type(strides) == int:
strides_h, strides_w = strides, strides
else:
strides_h, strides_w = strides
# 画像の数、高さ、幅、チャネル
un, uh, uw, uc = u.shape
# パディング後の高さ、幅
ph, pw = uh + padding_h*2, uw + padding_w*2
# パディング
pu = np.zeros((un, ph, pw, uc))
pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u
# プーリング後のデータ格納用
zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1
# 勾配格納領域確保
dpu = np.zeros((un, ph, pw, uc))
# プーリング後の高さ、幅分ループ
for i in range(zh):
for j in range(zw):
# dzijをプールサイズで割る
# dzs - (un, uc)
dzs = dz[:,i,j,:]/(pool_size_h*pool_size_w)
dzs = dzs.reshape(un, 1, 1, uc)
# プールサイズの高さ、幅分ループ
for k in range(pool_size_h):
for l in range(pool_size_w):
# 勾配設定
dpu[:, i*strides_h+k:i*strides_h+k+1, j*strides_w+l:j*strides_w+l+1, :] += dzs
# パディング部分の除去
du = dpu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :]
return du
for分の入れ子になりましたが、特に性能上の問題はありませんでした。
np.tileを利用しすれば、プールサイズの高さ、幅分のループは不要になることが分かりましたが、ほとんど性能が変わらなかったため分かりやすさの観点からこのままにしています。
flatten
最後に、畳み込み後の4次元データを全結合(Affine)で扱えるように、2次元に変換を行います。
flattenの実装
順伝播
高さ、幅、チャネル部分を1次元に変換します。reshapeするのみです。
def flatten2d(u):
# 画像の数、高さ、幅、チャネル
un, uh, uw, uc = u.shape
z = u.reshape(un, uh*uw*uc)
return z
逆伝播
逆伝播は、逆に、3次元の高さ、幅、チャネルに戻します。
def flatten2d_back(dz, u, z):
du = dz.reshape(u.shape)
return du
組み込み
「ディープラーニングを実装から学ぶ(8)実装変更」の実装に、CNNを組み込みます。
畳み込み
層の追加
畳み込み時にフィルタは、add_layerのunitにフィルタ数を、設定し、filter_sizeにフィルタ、paddinにパディング、stridesにストライドを設定するようにします。
フィルタ数を8とし、フィルタサイズ=5、パディング=2、ストライド=1を設置した例です。
model = add_layer(model, "conv", convolution2d, d=8, filter_size=5, padding=2, strides=1)
初期化
重さとして、フィルタサイズ$ \times $フィルタ数分を確保し初期化を行います。
def convolution2d_init_layer(d_prev, d, filter_size=2, padding=0, strides=1, weight_init_func=he_normal, weight_init_params={}, bias_init_func=zeros_b, bias_init_params={}):
# フィルタサイズ
if type(filter_size) == int:
filter_size_h, filter_size_w = filter_size, filter_size
else:
filter_size_h, filter_size_w = filter_size
# パディング
if type(padding) == int:
padding_h, padding_w = padding, padding
else:
padding_h, padding_w = padding
# ストライド
if type(strides) == int:
strides_h, strides_w = strides, strides
else:
strides_h, strides_w = strides
# 画像の高さ、幅、チャネル
uh, uw, uc = d_prev
# フィルターの数、高さ、幅、チャネル
fn, fh, fw, fc = d, filter_size_h, filter_size_w, d_prev[2]
# パディング後の高さ、幅
ph, pw = uh + padding_h*2, uw + padding_w*2
# 畳み込み後のデータ格納用
zh, zw = int((ph-fh)/strides_h)+1, int((pw-fw)/strides_w)+1
d_next = (zh, zw, fn)
# W - fn, fh, fw, fc
#fn, fh, fw, fc = d, filter_size_h, filter_size_w, d_prev.shape[2]
W = weight_init_func(fh*fw*fc, fn, **weight_init_params)
W = W.reshape((fn, fh, fw, fc))
b = bias_init_func(fn, **bias_init_params)
return d_next, {"W":W, "b":b, "padding":padding, "strides":strides}
def convolution2d_init_optimizer():
sW = {}
sb = {}
return {"sW":sW, "sb":sb}
順伝播、逆伝播、重みの更新
順伝播、逆伝播では、それぞれの関数を呼び出すようにします。update_weightで、重み、バイアスの更新を行います。
重み減衰にも対応します。対応方法は、affineと同じです。
def convolution2d_propagation(func, u, weights, weight_decay, learn_flag, **params):
z = func(u, weights["W"], weights["b"], padding=weights["padding"], strides=weights["strides"])
# 重み減衰対応
weight_decay_r = 0
if weight_decay is not None:
weight_decay_r = weight_decay["func"](weights["W"], **weight_decay["params"])
return {"u":u, "z":z}, weight_decay_r
def convolution2d_back_propagation(back_func, dz, us, weights, weight_decay, calc_du_flag, **params):
du, dW, db = back_func(dz, us["u"], weights["W"], weights["b"], padding=weights["padding"], strides=weights["strides"], calc_du_flag=calc_du_flag)
# 重み減衰対応
if weight_decay is not None:
dW = dW + weight_decay["back_func"](weights["W"], **weight_decay["params"])
return {"du":du, "dW":dW, "db":db}
def convolution2d_update_weight(func, du, weights, optimizer_stats, **params):
weights["W"], optimizer_stats["sW"] = func(weights["W"], du["dW"], **params, **optimizer_stats["sW"])
weights["b"], optimizer_stats["sb"] = func(weights["b"], du["db"], **params, **optimizer_stats["sb"])
return weights, optimizer_stats
プーリング
プーリングの層の定義例です。
マックスプーリングをプールサイズ=2、パディング=1、ストライド=2で設定しています。
model = add_layer(model, "max_pooling", max_pooling2d, pool_size=2, padding=1, strides=2)
プーリング層は、重さを持たないため、初期化で、プーリング後のサイズを求めるだけです。
def max_pooling2d_init_layer(d_prev, d, pool_size=2, padding=0, strides=None):
# ストライド設定
if strides is None:
strides = pool_size
# プールサイズ
if type(pool_size) == int:
pool_size_h, pool_size_w = pool_size, pool_size
else:
pool_size_h, pool_size_w = pool_size
# パディング
if type(padding) == int:
padding_h, padding_w = padding, padding
else:
padding_h, padding_w = padding
# ストライド
if type(strides) == int:
strides_h, strides_w = strides, strides
else:
strides_h, strides_w = strides
# 画像の高さ、幅、チャネル
uh, uw, uc = d_prev
# パディング後の高さ、幅
ph, pw = uh + padding_h*2, uw + padding_w*2
# プーリング後のデータ格納用
zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1
d_next = (zh, zw, uc)
return d_next, {}
def average_pooling2d_init_layer(d_prev, d, pool_size=2, padding=0, strides=None):
# ストライド設定
if strides is None:
strides = pool_size
# プールサイズ
if type(pool_size) == int:
pool_size_h, pool_size_w = pool_size, pool_size
else:
pool_size_h, pool_size_w = pool_size
# パディング
if type(padding) == int:
padding_h, padding_w = padding, padding
else:
padding_h, padding_w = padding
# ストライド
if type(strides) == int:
strides_h, strides_w = strides, strides
else:
strides_h, strides_w = strides
# 画像の高さ、幅、チャネル
uh, uw, uc = d_prev
# パディング後の高さ、幅
ph, pw = uh + padding_h*2, uw + padding_w*2
# プーリング後のデータ格納用
zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1
d_next = (zh, zw, uc)
return d_next, {}
flatten
層の定義です。flattenは、パラメータはありません。
model = add_layer(model, "flatten", flatten2d)
flattenも重さを持たないため、初期化でflatten後のサイズを求めるだけです。
def flatten2d_init_layer(d_prev, d):
d_next = d_prev[0]*d_prev[1]*d_prev[2]
return d_next, {}
実行例
CNNを実行してみます。
データ(画像)
画像データは、1次元で処理していました。
高さ、幅、チャネルの3次元で処理するため、あらかじめデータをreshapeします。MNISTは、白黒のため、チャネルは、1です。
nx_train = nx_train.reshape((nx_train.shape[0], 28, 28, 1))
nx_test = nx_test.reshape((nx_test.shape[0], 28, 28, 1))
モデル
畳み込み、マックスプーリング、全結合によるモデルを作成します。
例として、畳み込み部分は、フィルタ数を6、フィルタサイズを7としています。活性化関数は、ReLUです。
マックスプーリングは、プールサイズ=2(既定値)とします。
全結合は、今まで行っていた、100-50-10の階層モデルをそのまま利用しています。
model = create_model((28,28,1))
model = add_layer(model, "conv1", convolution2d, 6, filter_size=7)
model = add_layer(model, "reluc1", relu)
model = add_layer(model, "pooling1", max_pooling2d)
model = add_layer(model, "flatten", flatten2d)
model = add_layer(model, "affine1", affine, 100)
model = add_layer(model, "relua1", relu)
model = add_layer(model, "affine2", affine, 50)
model = add_layer(model, "relua2", relu)
model = add_layer(model, "affine3", affine, 10)
model = set_output(model, softmax)
model = set_error(model, cross_entropy_error)
学習
バッチサイズは、100として、30エポック学習してみます。
epoch = 30
batch_size = 100
np.random.seed(10)
model, optimizer, learn_info = learn(model, nx_train, t_train, nx_test, t_test, batch_size=batch_size, epoch=epoch)
実行結果
input - 0 (28, 28, 1)
conv1 convolution2d (28, 28, 1) (22, 22, 6)
reluc1 relu (22, 22, 6) (22, 22, 6)
pooling1 max_pooling2d (22, 22, 6) (11, 11, 6)
flatten flatten2d (11, 11, 6) 726
affine1 affine 726 100
relua1 relu 100 100
affine2 affine 100 50
relua2 relu 50 50
affine3 affine 50 10
output softmax 10
error cross_entropy_error
0 0.07975 2.58034561588 0.0773 2.58935648296
1 0.912583333333 0.283821423709 0.9667 0.104532411461
2 0.97325 0.0871521629503 0.9807 0.0617759030541
3 0.981733333333 0.0599540945957 0.9835 0.0506263259402
4 0.98515 0.0478125171804 0.9824 0.0544197303191
5 0.98755 0.0387084821671 0.9857 0.0431286090129
6 0.990516666667 0.0308306128231 0.9875 0.0372474273481
7 0.9915 0.0268400314089 0.9864 0.0425423202775
8 0.993316666667 0.0220682303396 0.9872 0.0392856988624
9 0.994633333333 0.0180485538536 0.9879 0.0378849975895
10 0.995483333333 0.0150215339979 0.9885 0.0400400907118
11 0.995866666667 0.0133006690729 0.9889 0.0371786578452
12 0.996966666667 0.0106675351944 0.9878 0.0431819648487
13 0.9973 0.00950805570707 0.9894 0.0378315592841
14 0.998016666667 0.00741429101193 0.9875 0.0425102406285
15 0.9985 0.00618680262641 0.9897 0.0383318882663
16 0.998616666667 0.00543502302013 0.9898 0.0382562129824
17 0.999133333333 0.00435419902991 0.9879 0.0414861122906
18 0.999016666667 0.00405959291219 0.9898 0.0413239474756
19 0.999483333333 0.00290562351368 0.9897 0.0397207654605
20 0.9997 0.00210381824759 0.9896 0.04057246413
21 0.999616666667 0.00204826697134 0.9901 0.0424649254543
22 0.999783333333 0.00167668925789 0.9902 0.0418876835005
23 0.99985 0.0013869041977 0.9894 0.0415403854871
24 0.999766666667 0.0014446994155 0.9904 0.040863073686
25 0.999883333333 0.00103046478336 0.9903 0.0407925786511
26 0.999883333333 0.0010185068358 0.9901 0.0427330248162
27 0.9999 0.000865082113849 0.9897 0.0431897308844
28 0.999916666667 0.000680996876102 0.9897 0.0426519497202
29 0.999966666667 0.000537026205558 0.9899 0.0422285960568
30 0.999983333333 0.000458706804451 0.9901 0.0433974335546
所要時間 = 38 分 19 秒
なんと、テストデータの正解率は、99%を超えました。
ただし、学習には、38分もかかりました。
時間はかかりましたが、CNNを利用することで、大幅に精度が向上しました。
参考
関数仕様
畳み込み関連の関数を追加しました。
# 層追加関数
model = add_layer(model, name, func, d=None, **kwargs)
# 引数
# model : モデル
# name : レイヤの名前
# func : 中間層の関数
# affine,sigmoid,tanh,relu,leaky_relu,prelu,rrelu,relun,srelu,elu,maxout,
# identity,softplus,softsign,step,dropout,batch_normalization,
# convolution2d,max_pooling2d,average_pooling2d,flatten2d
# d : ノード数
# affine,maxout,convolution2dの場合指定
# convolution2dの場合は、フィルタ数
# kwargs: 中間層の関数のパラメータ
# affine - weight_init_func=he_normal, weight_init_params={}, bias_init_func=zeros_b, bias_init_params={}
# weight_init_func - lecun_normal,lecun_uniform,glorot_normal,glorot_uniform,he_normal,he_uniform,normal_w,uniform_w,zeros_w,ones_w
# weight_init_params
# normal_w - mean=0, var=1
# uniform_w - min=0, max=1
# bias_init_func - normal_b,uniform_b,zeros_b,ones_b
# bias_init_params
# normal_b - mean=0, var=1
# uniform_b - min=0, max=1
# leaky_relu - alpha
# rrelu - min=0.0, max=0.1
# relun - n
# srelu - alpha
# elu - alpha
# maxout - unit=1, weight_init_func=he_normal, weight_init_params={}, bias_init_func=zeros_b, bias_init_params={}
# dropout - dropout_ratio=0.9
# batch_normalization - batch_norm_node=True, use_gamma_beta=True, use_train_stats=True, alpha=0.1
# convolution2d - padding=0, strides=1, weight_init_func=he_normal, weight_init_params={}, bias_init_func=zeros_b, bias_init_params={}
# max_pooling2d - pool_size=2, padding=0, strides=None
# average_pooling2d - pool_size=2, padding=0, strides=None
# 戻り値
# モデル
プログラム
「ディープラーニングを実装から学ぶ(8)実装変更」の追加分です。
基本的には、上で記述した通りですが、一部効率化のため見直しをしています。
# 畳み込み
def convolution2d(u, W, b, padding=0, strides=1):
# パディング
if type(padding) == int:
padding_h, padding_w = padding, padding
else:
padding_h, padding_w = padding
# ストライド
if type(strides) == int:
strides_h, strides_w = strides, strides
else:
strides_h, strides_w = strides
# 画像の数、高さ、幅、チャネル
un, uh, uw, uc = u.shape
# フィルタの数、高さ、幅、チャネル
fn, fh, fw, fc = W.shape
# パディング後の高さ、幅
ph, pw = uh + padding_h*2, uw + padding_w*2
# パディング
pu = np.zeros((un, ph, pw, uc))
pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u
# 畳み込み後の高さ、幅
zh, zw = int((ph-fh)/strides_h)+1, int((pw-fw)/strides_w)+1
# 畳み込み後の格納領域確保
z = np.zeros((un, zh, zw, fn))
# Wを事前にreshape&転置
# (fn, fh, fw, fc) => (fh*fw*fc, fn)
Wrt = W.reshape(fn, fh*fw*fc).T
# 畳み込み後の高さ、幅分ループ
for i in range(zh):
for j in range(zw):
# 画像からフィルタサイズ分切り出し
# ud - (un, fh, fw, uc)
ud = pu[:, i*strides_h:i*strides_h+fh, j*strides_w:j*strides_w+fw, :]
# 切り出した画像とフィルタの内積の計算
# (un, fh*fw*fc) @ (fh*fw*fx, fn) => (un, fn)
z[:, i, j, :] = np.dot(ud.reshape(un, fh*fw*fc), Wrt) + b
return z
def convolution2d_back(dz, u, W, b, padding=0, strides=1, calc_du_flag=True):
# パディング
if type(padding) == int:
padding_h, padding_w = padding, padding
else:
padding_h, padding_w = padding
# ストライド
if type(strides) == int:
strides_h, strides_w = strides, strides
else:
strides_h, strides_w = strides
# 画像の数、高さ、幅、チャネル
un, uh, uw, uc = u.shape
# フィルターの数、高さ、幅、チャネル
fn, fh, fw, fc = W.shape
# パディング後の高さ、幅
ph, pw = uh + padding_h*2, uw + padding_w*2
# パディング
pu = np.zeros((un, ph, pw, uc))
pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u
# 畳み込み後の高さ、幅
zh, zw = int((ph-fh)/strides_h)+1, int((pw-fw)/strides_w)+1
# 勾配格納領域確保
dpu = np.zeros((un, ph, pw, uc))
dW = np.zeros((fn, fh, fw, fc))
# Wを事前にreshape
# (fn, fh, fw, fc) => (fn, fh*fw*fc)
Wr = W.reshape(fn, fh*fw*fc)
# (fn, fh, fw, fc) => (fn, fh*fw*fc)
dWr = dW.reshape(fn, fh*fw*fc)
# 畳み込み後の高さ、幅分ループ
for i in range(zh):
for j in range(zw):
# dzijの取り出し
# dzs - (un, fn)
dzs = dz[:,i,j,:]
if calc_du_flag:
# u方向の勾配計算
# dpusr - (un,fn) @ (fn, fh*fw*fc) => (un, fh*fw*fc)
dpusr = np.dot(dzs, Wr)
# dpus - (un, fh, fw, uc)
dpus = dpusr.reshape(un, fh, fw, uc)
dpu[:, i*strides_h:i*strides_h+fh, j*strides_w:j*strides_w+fw, :] += dpus
# W方向の勾配計算
# pus - (un, fh*fw*uc)
pus = pu[:, i*strides_h:i*strides_h+fh, j*strides_w:j*strides_w+fw, :]
# pudr - (un, fh*fw*uc)
pusr = pus.reshape(un, fh*fw*uc)
# dWsr - (fn, un) @ (un, fh*fw*uc) => (fn, fh*fw*uc=fc)
dWsr = np.dot(dzs.T, pusr)
dWr += dWsr
# (fn, fh*fw*fc) => (fn, fh, fw, fc)
dW = dWr.reshape(fn, fh, fw, fc)
# パディング部分の除去
du = dpu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :]
# b方向の勾配計算
db = np.sum(dz.reshape(un*zh*zw, fn), axis=0)
return du, dW, db
def max_pooling2d(u, pool_size=2, padding=0, strides=None):
# ストライド設定
if strides is None:
strides = pool_size
# プールサイズ
if type(pool_size) == int:
pool_size_h, pool_size_w = pool_size, pool_size
else:
pool_size_h, pool_size_w = pool_size
# パディング
if type(padding) == int:
padding_h, padding_w = padding, padding
else:
padding_h, padding_w = padding
# ストライド
if type(strides) == int:
strides_h, strides_w = strides, strides
else:
strides_h, strides_w = strides
# 画像の数、高さ、幅、チャネル
un, uh, uw, uc = u.shape
# パディング後の高さ、幅
ph, pw = uh + padding_h*2, uw + padding_w*2
# パディング
pu = np.zeros((un, ph, pw, uc))
pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u
# プーリング後の高さ、幅
zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1
# プーリング後の格納領域確保
z = np.zeros((un, zh, zw, uc))
# プーリング後の高さ、幅分ループ
for i in range(zh):
for j in range(zw):
# 画像からプーリングサイズ分切り出し
# pus - (un, pool_size_h, pool_size_w, uc)
pus = pu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :]
# 切り出した画像の最大
z[:, i, j, :] = np.max(pus.reshape(un, pool_size_h*pool_size_w, uc), axis=1)
return z
def max_pooling2d_back(dz, u, z, pool_size=2, padding=0, strides=None):
# ストライド設定
if strides is None:
strides = pool_size
# プールサイズ
if type(pool_size) == int:
pool_size_h, pool_size_w = pool_size, pool_size
else:
pool_size_h, pool_size_w = pool_size
# パディング
if type(padding) == int:
padding_h, padding_w = padding, padding
else:
padding_h, padding_w = padding
# ストライド
if type(strides) == int:
strides_h, strides_w = strides, strides
else:
strides_h, strides_w = strides
# 画像の数、高さ、幅、チャネル
un, uh, uw, uc = u.shape
# パディング後の高さ、幅
ph, pw = uh + padding_h*2, uw + padding_w*2
# パディング
pu = np.zeros((un, ph, pw, uc))
pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u
# プーリング後のデータ格納用
zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1
# 勾配格納領域確保
dpu = np.zeros((un, ph, pw, uc))
# プーリング後の高さ、幅分ループ
for i in range(zh):
for j in range(zw):
# dzijの取り出し
# dzs - (un, fn)
dzs = dz[:,i,j,:]
# 最大の要素
pus = pu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :]
# 順番並び替え
pustr = pus.transpose(0, 3, 1, 2)
# 最大の要素
z_argmax = np.argmax(pustr.reshape(un*uc, pool_size_h*pool_size_w), axis=1)
# 勾配格納
dudrtr = np.zeros((un*uc, pool_size_h*pool_size_w))
dudrtr[np.arange(un*uc), z_argmax.ravel()] = dzs.ravel()
dudtr = dudrtr.reshape(un, uc, pool_size_h, pool_size_w)
# 順番元に戻す
dud = dudtr.transpose(0, 2, 3, 1)
# 勾配設定
dpu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :] += dud
du = dpu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :]
return du
def average_pooling2d(u, pool_size=2, padding=0, strides=None):
# ストライド設定
if strides is None:
strides = pool_size
# プールサイズ
if type(pool_size) == int:
pool_size_h, pool_size_w = pool_size, pool_size
else:
pool_size_h, pool_size_w = pool_size
# パディング
if type(padding) == int:
padding_h, padding_w = padding, padding
else:
padding_h, padding_w = padding
# ストライド
if type(strides) == int:
strides_h, strides_w = strides, strides
else:
strides_h, strides_w = strides
# 画像の数、高さ、幅、チャネル
un, uh, uw, uc = u.shape
# パディング後の高さ、幅
ph, pw = uh + padding_h*2, uw + padding_w*2
# パディング
pu = np.zeros((un, ph, pw, uc))
pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u
# プーリング後の高さ、幅
zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1
# プーリング後の格納領域確保
z = np.zeros((un, zh, zw, uc))
# プーリング後の高さ、幅分ループ
for i in range(zh):
for j in range(zw):
# 画像からプーリングサイズ分切り出し
# pus - (un, pool_size_h, pool_size_w, uc)
pus = pu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :]
# 切り出した画像の平均
z[:, i, j, :] = np.mean(pus.reshape(un, pool_size_h*pool_size_w, uc), axis=1)
return z
def average_pooling2d_back(dz, u, z, pool_size=2, padding=0, strides=None):
# ストライド設定
if strides is None:
strides = pool_size
# プールサイズ
if type(pool_size) == int:
pool_size_h, pool_size_w = pool_size, pool_size
else:
pool_size_h, pool_size_w = pool_size
# パディング
if type(padding) == int:
padding_h, padding_w = padding, padding
else:
padding_h, padding_w = padding
# ストライド
if type(strides) == int:
strides_h, strides_w = strides, strides
else:
strides_h, strides_w = strides
# 画像の数、高さ、幅、チャネル
un, uh, uw, uc = u.shape
# パディング後の高さ、幅
ph, pw = uh + padding_h*2, uw + padding_w*2
# パディング
pu = np.zeros((un, ph, pw, uc))
pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u
# プーリング後のデータ格納用
zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1
# 勾配格納領域確保
dpu = np.zeros((un, ph, pw, uc))
# プーリング後の高さ、幅分ループ
for i in range(zh):
for j in range(zw):
# dzijをプールサイズで割る
# dzs - (un, uc)
dzs = dz[:,i,j,:]/(pool_size_h*pool_size_w)
dzs = dzs.reshape(un, 1, 1, uc)
# プールサイズの高さ、幅分ループ
for k in range(pool_size_h):
for l in range(pool_size_w):
# 勾配設定
dpu[:, i*strides_h+k:i*strides_h+k+1, j*strides_w+l:j*strides_w+l+1, :] += dzs
# パディング部分の除去
du = dpu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :]
return du
def flatten2d(u):
# 画像の数、高さ、幅、チャネル
un, uh, uw, uc = u.shape
z = u.reshape(un, uh*uw*uc)
return z
def flatten2d_back(dz, u, z):
du = dz.reshape(u.shape)
return du
# convolution2d
def convolution2d_init_layer(d_prev, d, filter_size=2, padding=0, strides=1, weight_init_func=he_normal, weight_init_params={}, bias_init_func=zeros_b, bias_init_params={}):
# フィルタサイズ
if type(filter_size) == int:
filter_size_h, filter_size_w = filter_size, filter_size
else:
filter_size_h, filter_size_w = filter_size
# パディング
if type(padding) == int:
padding_h, padding_w = padding, padding
else:
padding_h, padding_w = padding
# ストライド
if type(strides) == int:
strides_h, strides_w = strides, strides
else:
strides_h, strides_w = strides
# 画像の高さ、幅、チャネル
uh, uw, uc = d_prev
# フィルターの数、高さ、幅、チャネル
fn, fh, fw, fc = d, filter_size_h, filter_size_w, d_prev[2]
# パディング後の高さ、幅
ph, pw = uh + padding_h*2, uw + padding_w*2
# 畳み込み後のデータ格納用
zh, zw = int((ph-fh)/strides_h)+1, int((pw-fw)/strides_w)+1
d_next = (zh, zw, fn)
# W - fn, fh, fw, fc
#fn, fh, fw, fc = d, filter_size_h, filter_size_w, d_prev.shape[2]
W = weight_init_func(fh*fw*fc, fn, **weight_init_params)
W = W.reshape((fn, fh, fw, fc))
b = bias_init_func(fn, **bias_init_params)
return d_next, {"W":W, "b":b, "padding":padding, "strides":strides}
def convolution2d_init_optimizer():
sW = {}
sb = {}
return {"sW":sW, "sb":sb}
def convolution2d_propagation(func, u, weights, weight_decay, learn_flag, **params):
z = func(u, weights["W"], weights["b"], padding=weights["padding"], strides=weights["strides"])
# 重み減衰対応
weight_decay_r = 0
if weight_decay is not None:
weight_decay_r = weight_decay["func"](weights["W"], **weight_decay["params"])
return {"u":u, "z":z}, weight_decay_r
def convolution2d_back_propagation(back_func, dz, us, weights, weight_decay, calc_du_flag, **params):
du, dW, db = back_func(dz, us["u"], weights["W"], weights["b"], padding=weights["padding"], strides=weights["strides"], calc_du_flag=calc_du_flag)
# 重み減衰対応
if weight_decay is not None:
dW = dW + weight_decay["back_func"](weights["W"], **weight_decay["params"])
return {"du":du, "dW":dW, "db":db}
def convolution2d_update_weight(func, du, weights, optimizer_stats, **params):
weights["W"], optimizer_stats["sW"] = func(weights["W"], du["dW"], **params, **optimizer_stats["sW"])
weights["b"], optimizer_stats["sb"] = func(weights["b"], du["db"], **params, **optimizer_stats["sb"])
return weights, optimizer_stats
# max_pooling2d
def max_pooling2d_init_layer(d_prev, d, pool_size=2, padding=0, strides=None):
# ストライド設定
if strides is None:
strides = pool_size
# プールサイズ
if type(pool_size) == int:
pool_size_h, pool_size_w = pool_size, pool_size
else:
pool_size_h, pool_size_w = pool_size
# パディング
if type(padding) == int:
padding_h, padding_w = padding, padding
else:
padding_h, padding_w = padding
# ストライド
if type(strides) == int:
strides_h, strides_w = strides, strides
else:
strides_h, strides_w = strides
# 画像の高さ、幅、チャネル
uh, uw, uc = d_prev
# パディング後の高さ、幅
ph, pw = uh + padding_h*2, uw + padding_w*2
# プーリング後のデータ格納用
zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1
d_next = (zh, zw, uc)
return d_next, {}
# average_pooling2d
def average_pooling2d_init_layer(d_prev, d, pool_size=2, padding=0, strides=None):
# ストライド設定
if strides is None:
strides = pool_size
# プールサイズ
if type(pool_size) == int:
pool_size_h, pool_size_w = pool_size, pool_size
else:
pool_size_h, pool_size_w = pool_size
# パディング
if type(padding) == int:
padding_h, padding_w = padding, padding
else:
padding_h, padding_w = padding
# ストライド
if type(strides) == int:
strides_h, strides_w = strides, strides
else:
strides_h, strides_w = strides
# 画像の高さ、幅、チャネル
uh, uw, uc = d_prev
# パディング後の高さ、幅
ph, pw = uh + padding_h*2, uw + padding_w*2
# プーリング後のデータ格納用
zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1
d_next = (zh, zw, uc)
return d_next, {}
# flatten2d
def flatten2d_init_layer(d_prev, d):
d_next = d_prev[0]*d_prev[1]*d_prev[2]
return d_next, {}