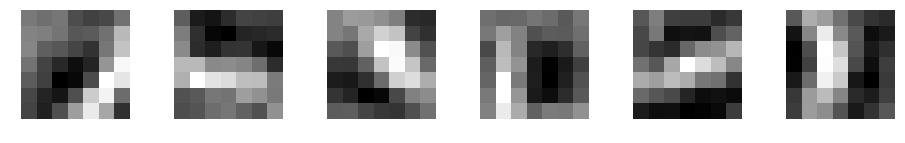ディープラーニングを実装から学ぶ～ （まとめ４）MNISTで99%も簡単！

「ディープラーニングを実装から学ぶ～ （まとめ１）」では、MNISTで約98%の正解率となりました。
MNISTの正解率 99%に挑戦してみましょう。畳み込みニューラルネットワーク(CNN)を実装してみます。

CNN

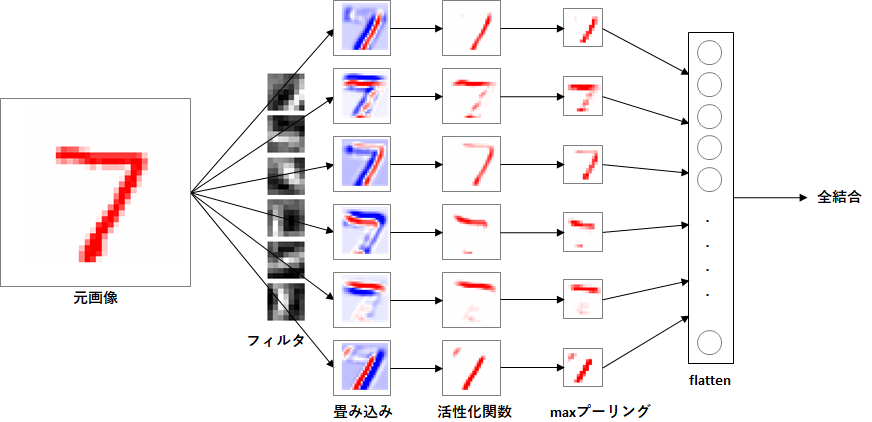
画像認識では、一般的にCNNが利用されます。今までは、ただのニューラルネットワーク（全結合）を用いていましたが、CNNに対応します。
CNNの実行例です。

それは、実装していきましょう。

実装

畳み込み層

画像（$ z $）は、４次元（画像の数、チャネル、高さ、幅）のデータです。
フィルタ（$ W $）も４次元（フィルタの数、チャネル、高さ、幅）です。
バイアス（$ b $）は、フィルタごとに設け、フィルタ数の1次元です。

    zn, zc, zh, zw = z.shape   # 画像の数、チャネル、高さ、幅
    fn, fc, fh, fw = W.shape   # フィルタの数、チャネル、高さ、幅

畳み込みの計算は、以下の式で表すことができます。

u_{spij} = \sum_{q=1}^{r}\sum_{k,l=1}^{m,n}z_{s,q,i+k,j+l}w_{pqkl}+b_{p}

それでは、順番に実装していきましょう。

順伝播

例えば、以下のように画像を$ z $、フィルタを$ W $とします。
畳み込み後のデータ$ u $は、以下となります。
（１番目のデータに対して１番目のフィルタを想定、チャネルは1を想定しています。画像は、高さ、幅の２次元、フィルタも高さ、幅の２次元で表しています。）

\begin{align}
z &=
\begin{pmatrix}
z_{11} & z_{12} & z_{13} \\
z_{21} & z_{22} & z_{23} \\
z_{31} & z_{32} & z_{33}
\end{pmatrix}
\\
\\
W &=
\begin{pmatrix}
w_{11} & w_{12} \\
w_{21} & w_{22}
\end{pmatrix}
\\
\\
u &=
\begin{pmatrix}
z_{11}w_{11}+z_{12}w_{12}+z_{21}w_{21}+z_{22}w_{22}+b & z_{12}w_{11}+z_{13}w_{12}+z_{22}w_{21}+z_{23}w_{22}+b \\
z_{21}w_{11}+z_{22}w_{12}+z_{31}w_{21}+z_{32}w_{22}+b & z_{22}w_{11}+z_{23}w_{12}+z_{32}w_{21}+z_{33}w_{22}+b
\end{pmatrix}
\end{align}

• 畳み込み後の高さ、幅、チャネル数

畳み込み後のサイズを考えます。
画像$ z $の高さと幅を$ zh,zw $、フィルタ$ f $の高さ、幅を$ fh,fw $とします。
畳み込み後の高さ($ uh $)、幅($ uw $)は、以下となります。
元のサイズより、フィルタサイズ-1個分、小さくなります。

uh = zh-fh+1\\
uw = zw-fw+1

上の例では、高さ、幅は、$ 3-2+1 = 2 $となります。

畳み込み後のチャネル数は、フィルタ数($ fn $)と同じになります。

    uh, uw = zh-fh+1, zw-fw+1  # 畳み込み後の高さ、幅

• 畳み込み

畳み込み後データ格納領域を確保し、高さ、幅分ループし畳み込みの計算を行います。

    # 畳み込み後の格納領域確保
    u = np.zeros((zn, fn, uh, uw))
    # 畳み込み後の高さ、幅分ループ
    for i in range(uh):
        for j in range(uw):

画像から畳み込みを行う領域を切り出します。

            # 画像からフィルタサイズ分切り出し
            zs = z[:, :, i:i+fh, j:j+fw]

たとえば、最初のデータは、以下となります。

zs =
\begin{pmatrix}
z_{11} & z_{12} \\
z_{21} & z_{22}
\end{pmatrix}

切り出した画像とフィルタを掛けて加えます。内積を利用すると簡単に計算できますが、そのままでは内積できません。切り出した画像は、チャネル、高さ、幅を１次元にするようreshapeを行います。フィルタも同様にreshapeし転置します。

            # データ件数分、内積を行えるようにreshape
            zsr = zs.reshape(zn, zc*fh*fw)
            Wrt = W.reshape(fn, fc*fh*fw).T

reshape後です。

\begin{align}
zsr &=
\begin{pmatrix}
z_{11} & z_{12} & z_{21} & z_{22}
\end{pmatrix}
\\
Wrt &=
\begin{pmatrix}
w_{11} \\
w_{12} \\
w_{21} \\
w_{22}
\end{pmatrix}
\end{align}

内積を取ります。バイアスのbも加えます。

            # 切り出した画像とフィルタの内積の計算
            u[:, :, i, j] = np.dot(zsr, Wrt) + b

\begin{pmatrix}
z_{11} & z_{12} & z_{21} & z_{22}
\end{pmatrix}
\begin{pmatrix}
w_{11} \\
w_{12} \\
w_{21} \\
w_{22}
\end{pmatrix}
+ b
= z_{11}w_{11}+z_{12}w_{12}+z_{21}w_{21}+z_{22}w_{22}+b

畳み込み関数全体です。

def convolution2d(z, W, b):
    zn, zc, zh, zw = z.shape   # 画像の数、チャネル、高さ、幅
    fn, fc, fh, fw = W.shape   # フィルタの数、チャネル、高さ、幅
    uh, uw = zh-fh+1, zw-fw+1  # 畳み込み後の高さ、幅
    # 畳み込み後の格納領域確保
    u = np.zeros((zn, fn, uh, uw))
    # 畳み込み後の高さ、幅分ループ
    for i in range(uh):
        for j in range(uw):
            # 画像からフィルタサイズ分切り出し
            zs = z[:, :, i:i+fh, j:j+fw]
            # データ件数分、内積を行えるようにreshape
            zsr = zs.reshape(zn, zc*fh*fw)
            Wrt = W.reshape(fn, fc*fh*fw).T
            # 切り出した画像とフィルタの内積の計算
            u[:, :, i, j] = np.dot(zsr, Wrt) + b
    return u

逆伝播

畳み込みの勾配格納領域を確保します。

    # 勾配格納領域確保
    dz = np.zeros_like(z)
    dW = np.zeros_like(W)
    db = np.zeros_like(b)

順伝播と同じように畳み込み後の高さ、幅分ループし、後ろからの勾配をひとつづつ取り出して計算を行います。

    # 畳み込み後の高さ、幅分ループ
    for i in range(uh):
        for j in range(uw):
            # 勾配の取り出し
            dus = du[:, :, i, j]

• $ z $方向

$ u_{11} $は、以下の式で表せます。

u_{11} = z_{11}w_{11}+z_{12}w_{12}+z_{21}w_{21}+z_{22}w_{22}+b

$ z_{11} $で偏微分します。

\frac{\partial u_{11}}{\partial z_{11}} = w_{11}

勾配は、$ w_{11} $となりました。最終的な勾配は、後ろからの$ du_{11} $を掛けて以下となります。

du_{11} \times w_{11}

$ z $全体では、以下となります。

\begin{pmatrix}
du_{11}w_{11} & du_{11}w_{12} \\
du_{11}w_{21} & du_{11}w_{22}
\end{pmatrix}

フィルタを一次元にreshapeし、内積を取ります。

            # z方向の勾配計算
            Wr = W.reshape(fn, fc*fh*fw)
            dzs = np.dot(dus, Wr)

\begin{pmatrix}
du_{11}
\end{pmatrix}
\begin{pmatrix}
w_{11} & w_{12} & w_{21} & w_{22}
\end{pmatrix}
= 
\begin{pmatrix}
du_{11}w_{11} & du_{11}w_{12} & du_{11}w_{21} & du_{11}w_{22}
\end{pmatrix}

これを畳み込みの元の位置に返します。

            dz[:, :, i:i+fh, j:j+fw] += np.dot(dus, Wr).reshape(zn, zc, fh, fw)

\begin{pmatrix}
du_{11}w_{11} & du_{11}w_{12} & 0 \\
du_{11}w_{21} & du_{11}w_{22} & 0 \\
0             & 0             & 0
\end{pmatrix}

加えているのは、畳み込みでは、$ z $が複数の場所で利用されるためです。例えば、$ z_{22} $は、4箇所全部で利用されていますよね。
全部だと以下のようになります。

dz = 
\begin{pmatrix}
du_{11}w_{11} & du_{11}w_{12}+du_{12}w_{11} & du_{12}w_{12} \\
du_{11}w_{21}+du_{21}w_{11} & du_{11}w_{22}+du_{12}w_{21}+du_{21}w_{12}+du_{22}w_{11} & du_{12}w_{22}+du_{22}w_{12} \\
du_{21}w_{21}             & du_{21}w_{22}+du_{22}w_{21}             & du_{22}w_{22}
\end{pmatrix}

• $ W $方向

$ u_{11} $は、以下でした。

u_{11} = z_{11}w_{11}+z_{12}w_{12}+z_{21}w_{21}+z_{22}w_{22}+b

$ w_{11} $で偏微分します。

\frac{\partial u_{11}}{\partial w_{11}} = z_{11}

勾配は、$ z_{11} $となりました。最終的な勾配は、後ろからの$ du_{11} $を掛けて以下となります。

du_{11} \times z_{11}

$ z $をreshapeし、内積を取ります。

            # W方向の勾配計算
            zsr = z[:, :, i:i+fh, j:j+fw].reshape(zn, zc*fh*fw)
            dWr = np.dot(dus.T, zsr)

\begin{pmatrix}
du_{11}
\end{pmatrix}
\begin{pmatrix}
z_{11} & z_{12} & z_{21} & z_{22}
\end{pmatrix}
= 
\begin{pmatrix}
du_{11}z_{11} & du_{11}z_{12} & du_{11}z_{21} & du_{11}z_{22}
\end{pmatrix}

これをフィルタの元の位置に返します。

            dW += dWr.reshape(fn, fc, fh, fw)

\begin{pmatrix}
du_{11}z_{11} & du_{11}z_{12} \\
du_{11}z_{21} & du_{11}z_{22}
\end{pmatrix}

$ u_{11} $について考えましたが、同様に他も各フィルタに返されます。
全部だと以下のようになります。

dW = 
\begin{pmatrix}
du_{11}z_{11}+du_{12}z_{12}+du_{21}z_{21}+du_{22}z_{22} & du_{11}z_{12}+du_{12}z_{13}+du_{21}z_{22}+du_{22}z_{23} \\
du_{11}z_{21}+du_{12}z_{22}+du_{21}z_{31}+du_{22}z_{32} & du_{11}z_{22}+du_{12}z_{23}+du_{21}z_{32}+du_{22}z_{33}
\end{pmatrix}

• $ b $方向

$ u_{11} $は、以下でした。

u_{11} = z_{11}w_{11}+z_{12}w_{12}+z_{21}w_{21}+z_{22}w_{22}+b

$ b $で偏微分します。

\frac{\partial u_{11}}{\partial b} = 1

勾配は、$ 1 $となりました。最終的な勾配は、後ろからの$ du_{11} $を掛けて以下となります。

du_{11} \times 1 = du_{11}

            # b方向の勾配計算
            db += np.sum(dus, axis=0)

$ u_{11} $について考えましたが、同様に他もバイアスに返されます。
全部だと以下のようになります。

db = du_{11}+du_{12}+du_{21}+du_{22}

畳み込みの逆伝播関数全体です

def convolution2d_back(du, z, W, b):
    zn, zc, zh, zw = z.shape   # 画像の数、チャネル、高さ、幅
    fn, fc, fh, fw = W.shape   # フィルタの数、チャネル、高さ、幅
    uh, uw = zh-fh+1, zw-fw+1  # 畳み込み後の高さ、幅
    # 勾配格納領域確保
    dz = np.zeros_like(z)
    dW = np.zeros_like(W)
    db = np.zeros_like(b)
    # 畳み込み後の高さ、幅分ループ
    for i in range(uh):
        for j in range(uw):
            # 勾配の取り出し
            dus = du[:, :, i, j]
            # z方向の勾配計算
            Wr = W.reshape(fn, fc*fh*fw)
            dzs = np.dot(dus, Wr)
            dz[:, :, i:i+fh, j:j+fw] += dzs.reshape(zn, zc, fh, fw)
            # W方向の勾配計算
            zsr = z[:, :, i:i+fh, j:j+fw].reshape(zn, zc*fh*fw)
            dWr = np.dot(dus.T, zsr)
            dW += dWr.reshape(fn, fc, fh, fw)
            # b方向の勾配計算
            db += np.sum(dus, axis=0)
    return dz, dW, db

プーリング層

プーリング層により画像を縮小します。プーリングには、各種手法があるようですが、ここでは最も一般的なmaxプーリングとします。

画像（$ z $）は、４次元（画像の数、チャネル、高さ、幅）のデータです。

    zn, zc, zh, zw = z.shape        # 画像の数、チャネル、高さ、幅

maxプーリングの計算は、以下の式で表すことができます。

u_{spij} = \max_{(k,l)\in P_{ij}}z_{spkl}

ただし、$ P_{ij} $は、$ (i,j) $のプーリング範囲

それでは、順番に実装していきましょう。

順伝播

画像を$ z $とし、maxプーリング適用後のデータ$ u $は、以下となります。
（１番目のデータ、１番目のチャネルを想定）

\begin{align}
z &=
\begin{pmatrix}
z_{11} & z_{12} & z_{13} & z_{14} \\
z_{21} & z_{22} & z_{23} & z_{24} \\
z_{31} & z_{32} & z_{33} & z_{34} \\
z_{41} & z_{42} & z_{43} & z_{44}
\end{pmatrix}
\\
\\
u &=
\begin{pmatrix}
max(z_{11},z_{12},z_{21},z_{22})  & max(z_{13},z_{14},z_{23},z_{24}) \\
max(z_{31},z_{32},z_{41},z_{42})  & max(z_{33},z_{34},z_{43},z_{44})
\end{pmatrix}
\end{align}

• プーリング後の高さ、幅、チャネル数

プーリング後のサイズを考えます。
画像$ z $の高さと幅を$ zh,zw $、プールサイズ$ ps=2 $とします。
プーリング後の高さ($ uh $)、幅($ uw $)は、以下となります。
元のサイズの半分になります。

uh = zh/ps\\
uw = zw/ps

上の例では、高さ、幅は、$ 4/2 = 2 $となります。

チャネルごとに、最大値を求めるためプーリング後のチャネル数は、元のチャネル数と同じです。

    uh, uw = int(zh/ps), int(zw/ps) # プーリング後の高さ、幅

• maxプーリング

プーリング後のデータ格納領域を確保し、高さ、幅分ループしmaxプーリングの計算を行います。

    # プーリング後の格納領域確保
    u = np.zeros((zn, zc, uh, uw))
    # プーリング後の高さ、幅分ループ
    for i in range(uh):
        for j in range(uw):

画像からプーリングを行う領域を切り出します。

            # 画像からプーリングサイズ分切り出し
            zs = z[:, :, i*ps:i*ps+ps, j*ps:j*ps+ps]

たとえば、最初のデータは、以下となります。

zs =
\begin{pmatrix}
z_{11} & z_{12} \\
z_{21} & z_{22}
\end{pmatrix}

高さ、幅部分をreshapeし、一次元にします。その後に最大値を求めます。最大は、$ ps*ps $の部分から求めるため、$ axis=2 $を指定します。

            # 切り出した画像の最大
            u[:, :, i, j] = np.max(zs.reshape(zn, zc, ps*ps), axis=2)

maxプーリング関数全体です。

def max_pooling2d(z, ps=2):
    zn, zc, zh, zw = z.shape        # 画像の数、チャネル、高さ、幅
    uh, uw = int(zh/ps), int(zw/ps) # プーリング後の高さ、幅
    # プーリング後の格納領域確保
    u = np.zeros((zn, zc, uh, uw))
    # プーリング後の高さ、幅分ループ
    for i in range(uh):
        for j in range(uw):
            # 画像からプーリングサイズ分切り出し
            zs = z[:, :, i*ps:i*ps+ps, j*ps:j*ps+ps]
            # 切り出した画像の最大
            u[:, :, i, j] = np.max(zs.reshape(zn, zc, ps*ps), axis=2)
    return u

逆伝播

プーリングの勾配格納領域を確保します。

    # 勾配格納領域確保
    dz = np.zeros_like(z)

順伝播と同じようにプーリング後の高さ、幅分ループし、後ろからの勾配をひとつづつ取り出して計算を行います。

    # プーリング後の高さ、幅分ループ
    for i in range(uh):
        for j in range(uw):
            # 勾配の取り出し
            dus = du[:, :, i, j]

• $ z $方向

$ u_{11} $は、以下の式で表せます。

u_{11} = max(z_{11},z_{12},z_{21},z_{22})

仮に、$ z_{11} $が最大だとします。

u_{11} = z_{11}

$ z_{11} $で偏微分します。

\frac{\partial u_{11}}{\partial z_{11}} = 1

勾配は、$ 1 $となりました。最終的な勾配は、後ろからの$ du_{11} $を掛けて以下となります。

du_{11} \times 1 = du_{11}

仮に、$ z_{11} $を最大と仮定しました。それ以外の$ z_{12},z_{21},z_{22} $の偏微分は$ 0 $となります。

\frac{\partial u_{11}}{\partial z_{12}} = 0\\
\frac{\partial u_{11}}{\partial z_{21}} = 0\\
\frac{\partial u_{11}}{\partial z_{22}} = 0

$ z $全体では、以下となります。

\begin{pmatrix}
du_{11} & 0 \\
0 & 0
\end{pmatrix}

単に最大のところのみに、返せばよいのですが、プログラムでは単純ではありません。

まず、最大の要素の場所を求めます。argmaxで最大の場所を求められますが、1次元にしないと求められません。高さ、幅を1次元にし、軸を1として最大の位置を計算します。

            # 最大の要素
            zs = z[:, :, i*ps:i*ps+ps, j*ps:j*ps+ps]
            zs_argmax = np.argmax(zs.reshape(zn*zc, ps*ps), axis=1)

arangeで順番を生成し、ひとつずつ最大値を設定します。

            # 勾配格納
            dzr = np.zeros((zn*zc, ps*ps))
            dzr[np.arange(zn*zc), zs_argmax.flatten()] = dus.flatten()

reshapeし、もとの位置に戻します。

            # 勾配設定
            dz[:, :, i*ps:i*ps+ps, j*ps:j*ps+ps] += dzr.reshape(zn, zc, ps, ps)

単に、最大値の位置に$ du $を返すだけですが、複雑になりました。
maxプーリングの逆伝播関数全体です。

def max_pooling2d_back(du, z, ps=2):
    zn, zc, zh, zw = z.shape        # 画像の数、チャネル、高さ、幅
    uh, uw = int(zh/ps), int(zw/ps) # プーリング後の高さ、幅
    # 勾配格納領域確保
    dz = np.zeros_like(z)
    # プーリング後の高さ、幅分ループ
    for i in range(uh):
        for j in range(uw):
            # 勾配の取り出し
            dus = du[:, :, i, j]
            # 最大の要素
            zs = z[:, :, i*ps:i*ps+ps, j*ps:j*ps+ps]
            zs_argmax = np.argmax(zs.reshape(zn*zc, ps*ps), axis=1)
            # 勾配格納
            dzr = np.zeros((zn*zc, ps*ps))
            dzr[np.arange(zn*zc), zs_argmax.flatten()] = dus.flatten()
            # 勾配設定
            dz[:, :, i*ps:i*ps+ps, j*ps:j*ps+ps] += dzr.reshape(zn, zc, ps, ps)
    return dz

flatten

畳み込み後は、チャネル、高さ、幅の3次元のデータです。全結合を行えるように、1次元に変換します。

順伝播

単に、チャネル、高さ、幅をreshapeし、1次元にします。

def flatten2d(u):
    un, uc, uh, uw = u.shape # 画像の数、チャネル、高さ、幅
    z = u.reshape(un, uc*uh*uw)
    return z

逆伝播

逆伝播は、逆に1次元からチャネル、高さ、幅の3次元にreshapeします。$ du $は、$ u $と同じshapeのため、$ u.shape $にreshapeしています。

def flatten2d_back(dz, u):
    du = dz.reshape(u.shape)
    return du

学習プログラム

学習

一般的に、畳み込み、プーリングの後に全結合層を置きます。
今までの全結合層の前に、畳み込み層とmaxプーリング層を追加しました。活性化関数は、reluとし、全結合層の前には、flattenを入れています。
maxプーリング層は、重み、バイアスを持たないため、重み、アイアスの更新は、畳み込み層のみの追加です。
1ステップずつ書いているので長くなりましたね。流れは、見えると思います。

def learn(x, t, Wc, bc, W1, b1, W2, b2, W3, b3, lr):
    # 順伝播
    uc = convolution2d(x, Wc, bc)
    zc = relu(uc)
    up = max_pooling2d(zc)
    zp = flatten2d(up)
    u1 = affine(zp, W1, b1)
    z1 = relu(u1)
    u2 = affine(z1, W2, b2)
    z2 = relu(u2)
    u3 = affine(z2, W3, b3)
    y  = softmax(u3)
    # 逆伝播
    dy = softmax_cross_entropy_error_back(y, t)
    dz2, dW3, db3 = affine_back(dy, z2, W3, b3)
    du2 = relu_back(dz2, u2)
    dz1, dW2, db2 = affine_back(du2, z1, W2, b2)
    du1 = relu_back(dz1, u1)
    dzp, dW1, db1 = affine_back(du1, zp, W1, b1)
    dup = flatten2d_back(dzp, up)
    dzc = max_pooling2d_back(dup, zc)
    duc = relu_back(dzc, uc)
    dx, dWc, dbc = convolution2d_back(duc, x, Wc, bc)
    # 重み、バイアスの更新
    Wc = Wc - lr * dWc
    bc = bc - lr * dbc
    W1 = W1 - lr * dW1
    b1 = b1 - lr * db1
    W2 = W2 - lr * dW2
    b2 = b2 - lr * db2
    W3 = W3 - lr * dW3
    b3 = b3 - lr * db3

    return y, Wc, bc, W1, b1, W2, b2, W3, b3

後述しますが、効率化のため、$ y $も返却するようにしました。

予測

予測プログラムは、学習プログラムの順伝播の部分のみです。

def predict(x, Wc, bc, W1, b1, W2, b2, W3, b3):
    # 順伝播
    uc = convolution2d(x, Wc, bc)
    zc = relu(uc)
    up = max_pooling2d(zc)
    zp = flatten2d(up)
    u1 = affine(zp, W1, b1)
    z1 = relu(u1)
    u2 = affine(z1, W2, b2)
    z2 = relu(u2)
    u3 = affine(z2, W3, b3)
    y  = softmax(u3)
    return y

実行プログラム

畳み込み対応のため、畳み込み関連処理を追加しています。
また、一部、効率化のため見直しを行っています。

「ディープラーニングを実装から学ぶ～ (まとめ１）実装は、実は簡単」からの変更部分です。

データをチャネル、高さ、幅にreshapeしています。MNISTは、白黒画像のため、チャネル数宇は、1です。

x_train = x_train.reshape(x_train.shape[0], 1, 28, 28)
x_test  = x_test.reshape(x_test.shape[0], 1, 28, 28)

ノード数の設定です。
ここでは、畳み込み時のフィルタ数を6、フィルタサイズを7としています。また、maxプーリングのプールサイズは、2です。
全結合層のノード数を決めるため、畳み込み後、プーリング後の高さ、幅を求めています。

# ノード数設定
un, uc, uh, uw = nx_train.shape
fn, fc, fh, fw = 6, 1, 7, 7 # フィルタサイズ
ps = 2                      # プーリングサイズ
zh, zw = uh-fh+1, uw-fw+1   # 畳み込み後の高さ、幅
zh, zw = int(zh/ps), int(zw/ps) # プーリング後の高さ、幅
d0 = fn * zh * zw

畳み込み層の重み、バイアスも全結合層同様に初期化します。

# 重みの初期化(-0.1～0.1の乱数)
Wc = np.random.rand(fn, fc, fh, fw) * 0.2 - 0.1
# バイアスの初期化(0)
bc = np.zeros(fn)

学習前と学習中の1エポックごとに、学習データとテストデータの正解率を計算していました。畳み込みでは、大量のメモリが必要となるため、バッチサイズごとに分割し予測することにしました。
また、予測にも時間がかかるため、学習データについては、学習時の予測値を利用して正解率を計算することにしました。このために、learn関数で、yを返却するようにしました。
エポックごとの正解率、誤差の表示部分が長くなったため関数としてまとめ、呼び出すことにしました。
正解率、誤差を表示する関数です。

def print_metrics(epoche, x_train, t_train, y_train, x_test, t_test, y_test, Wc, bc, W1, b1, W2, b2, W3, b3):
    # 予測（学習データ）
    if y_train is None:
        y_train = np.zeros_like(t_train)
        for j in range(0, x_train.shape[0], batch_size):
            y_train[j:j+batch_size] = predict(x_train[j:j+batch_size], Wc, bc, W1, b1, W2, b2, W3, b3)
    # 予測（テストデータ）
    if y_test is None:
        y_test = np.zeros_like(t_test)
        for j in range(0, x_test.shape[0], batch_size):
            y_test[j:j+batch_size] = predict(x_test[j:j+batch_size], Wc, bc, W1, b1, W2, b2, W3, b3)
    # 正解率、誤差表示
    train_rate, train_err = accuracy_rate(y_train, t_train), cross_entropy_error(y_train, t_train)
    test_rate, test_err = accuracy_rate(y_test, t_test), cross_entropy_error(y_test, t_test)
    print("{0:3d} train_rate={1:6.2f}% test_rate={2:6.2f}% train_err={3:8.5f} test_err={4:8.5f}".format(epoche, train_rate*100, test_rate*100, train_err, test_err))

もう1点、エポックごとに学習データをソートするようにしました。基本的に学習時はソートするのが良いようです。

学習部分の抜粋です。np.arangeでインデックスを作成し、np.random.shuffleで、ソートしています。ソート後のデータで学習を行えるように、y_train[idx[j:j+batch_size]]のように、ソート後のインデックスで学習データを定めています。

for i in range(epoch):
    # データシャッフル
    idx = np.arange(nx_train.shape[0])
    np.random.shuffle(idx)

    # 学習
    y_train = np.zeros_like(t_train)
    for j in range(0, nx_train.shape[0], batch_size):
        y_train[idx[j:j+batch_size]], Wc, bc, W1, b1, W2, b2, W3, b3 = learn(nx_train[idx[j:j+batch_size]], t_train[idx[j:j+batch_size]], Wc, bc, W1, b1, W2, b2, W3, b3, lr)

なお、学習率は、0.2に変更しました。また、学習エポック数は、30としました。

学習の実行

データ

データは、MNISTのページからダウンロードしてください。

• train-images-idx3-ubyte.gz: 学習用画像
• train-labels-idx1-ubyte.gz: 学習用正解ラベル
• t10k-images-idx3-ubyte.gz: テスト用画像
• t10k-labels-idx1-ubyte.gz: テスト用正解ラベル

データは、dataフォルダに格納することを想定しています。別のフォルダに格納した場合は、load_mnistのパラメータを変更してください。
（「ディープラーニングを実装から学ぶ～ (まとめ１）実装は、実は簡単」では、データを'c:\mnist\'に格納していましたが、格納場所を変更しました。）

プログラム全体

関数

既存

import numpy as np
# affine変換
def affine(z, W, b):
    return np.dot(z, W) + b
# affine変換勾配
def affine_back(du, z, W, b):
    dz = np.dot(du, W.T)
    dW = np.dot(z.T, du)
    db = np.dot(np.ones(z.shape[0]).T, du)
    return dz, dW, db
# 活性化関数(ReLU)
def relu(u):
    return np.maximum(0, u)
# 活性化関数(ReLU)勾配
def relu_back(dz, u):
    return dz * np.where(u > 0, 1, 0)
# 活性化関数(softmax)
def softmax(u):
    max_u = np.max(u, axis=1, keepdims=True)
    exp_u = np.exp(u-max_u)
    return exp_u/np.sum(exp_u, axis=1, keepdims=True)
# 誤差(交差エントロピー）
def cross_entropy_error(y, t):
    return -np.sum(t * np.log(np.maximum(y,1e-7)))/y.shape[0]
# 誤差(交差エントロピー）＋活性化関数(softmax)勾配
def softmax_cross_entropy_error_back(y, t):
    return (y - t)/y.shape[0]

CNN対応追加

def convolution2d(z, W, b):
    zn, zc, zh, zw = z.shape   # 画像の数、チャネル、高さ、幅
    fn, fc, fh, fw = W.shape   # フィルタの数、チャネル、高さ、幅
    uh, uw = zh-fh+1, zw-fw+1  # 畳み込み後の高さ、幅
    # 畳み込み後の格納領域確保
    u = np.zeros((zn, fn, uh, uw))
    # 畳み込み後の高さ、幅分ループ
    for i in range(uh):
        for j in range(uw):
            # 画像からフィルタサイズ分切り出し
            zs = z[:, :, i:i+fh, j:j+fw]
            # データ件数分、内積を行えるようにreshape
            zsr = zs.reshape(zn, zc*fh*fw)
            Wrt = W.reshape(fn, fc*fh*fw).T
            # 切り出した画像とフィルタの内積の計算
            u[:, :, i, j] = np.dot(zsr, Wrt) + b
    return u

def convolution2d_back(du, z, W, b):
    zn, zc, zh, zw = z.shape   # 画像の数、チャネル、高さ、幅
    fn, fc, fh, fw = W.shape   # フィルタの数、チャネル、高さ、幅
    uh, uw = zh-fh+1, zw-fw+1  # 畳み込み後の高さ、幅
    # 勾配格納領域確保
    dz = np.zeros_like(z)
    dW = np.zeros_like(W)
    db = np.zeros_like(b)
    # 畳み込み後の高さ、幅分ループ
    for i in range(uh):
        for j in range(uw):
            # 勾配の取り出し
            dus = du[:, :, i, j]
            # z方向の勾配計算
            Wr = W.reshape(fn, fc*fh*fw)
            dzs = np.dot(dus, Wr)
            dz[:, :, i:i+fh, j:j+fw] += dzs.reshape(zn, zc, fh, fw)
            # W方向の勾配計算
            zsr = z[:, :, i:i+fh, j:j+fw].reshape(zn, zc*fh*fw)
            dWr = np.dot(dus.T, zsr)
            dW += dWr.reshape(fn, fc, fh, fw)
            # b方向の勾配計算
            db += np.sum(dus, axis=0)
    return dz, dW, db

def max_pooling2d(z, ps=2):
    zn, zc, zh, zw = z.shape        # 画像の数、チャネル、高さ、幅
    uh, uw = int(zh/ps), int(zw/ps) # プーリング後の高さ、幅
    # プーリング後の格納領域確保
    u = np.zeros((zn, zc, uh, uw))
    # プーリング後の高さ、幅分ループ
    for i in range(uh):
        for j in range(uw):
            # 画像からプーリングサイズ分切り出し
            zs = z[:, :, i*ps:i*ps+ps, j*ps:j*ps+ps]
            # 切り出した画像の最大
            u[:, :, i, j] = np.max(zs.reshape(zn, zc, ps*ps), axis=2)
    return u

def max_pooling2d_back(du, z, ps=2):
    zn, zc, zh, zw = z.shape        # 画像の数、チャネル、高さ、幅
    uh, uw = int(zh/ps), int(zw/ps) # プーリング後の高さ、幅
    # 勾配格納領域確保
    dz = np.zeros_like(z)
    # プーリング後の高さ、幅分ループ
    for i in range(uh):
        for j in range(uw):
            # 勾配の取り出し
            dus = du[:, :, i, j]
            # 最大の要素
            zs = z[:, :, i*ps:i*ps+ps, j*ps:j*ps+ps]
            zs_argmax = np.argmax(zs.reshape(zn*zc, ps*ps), axis=1)
            # 勾配格納
            dzr = np.zeros((zn*zc, ps*ps))
            dzr[np.arange(zn*zc), zs_argmax.flatten()] = dus.flatten()
            # 勾配設定
            dz[:, :, i*ps:i*ps+ps, j*ps:j*ps+ps] += dzr.reshape(zn, zc, ps, ps)
    return dz

def flatten2d(u):
    un, uc, uh, uw = u.shape # 画像の数、チャネル、高さ、幅
    z = u.reshape(un, uc*uh*uw)
    return z

def flatten2d_back(dz, u):
    du = dz.reshape(u.shape)
    return du

学習プログラム

学習

def learn(x, t, Wc, bc, W1, b1, W2, b2, W3, b3, lr):
    # 順伝播
    uc = convolution2d(x, Wc, bc)
    zc = relu(uc)
    up = max_pooling2d(zc)
    zp = flatten2d(up)
    u1 = affine(zp, W1, b1)
    z1 = relu(u1)
    u2 = affine(z1, W2, b2)
    z2 = relu(u2)
    u3 = affine(z2, W3, b3)
    y  = softmax(u3)
    # 逆伝播
    dy = softmax_cross_entropy_error_back(y, t)
    dz2, dW3, db3 = affine_back(dy, z2, W3, b3)
    du2 = relu_back(dz2, u2)
    dz1, dW2, db2 = affine_back(du2, z1, W2, b2)
    du1 = relu_back(dz1, u1)
    dzp, dW1, db1 = affine_back(du1, zp, W1, b1)
    dup = flatten2d_back(dzp, up)
    dzc = max_pooling2d_back(dup, zc)
    duc = relu_back(dzc, uc)
    dx, dWc, dbc = convolution2d_back(duc, x, Wc, bc)
    # 重み、バイアスの更新
    Wc = Wc - lr * dWc
    bc = bc - lr * dbc
    W1 = W1 - lr * dW1
    b1 = b1 - lr * db1
    W2 = W2 - lr * dW2
    b2 = b2 - lr * db2
    W3 = W3 - lr * dW3
    b3 = b3 - lr * db3

    return y, Wc, bc, W1, b1, W2, b2, W3, b3

予測

def predict(x, Wc, bc, W1, b1, W2, b2, W3, b3):
    # 順伝播
    uc = convolution2d(x, Wc, bc)
    zc = relu(uc)
    up = max_pooling2d(zc)
    zp = flatten2d(up)
    u1 = affine(zp, W1, b1)
    z1 = relu(u1)
    u2 = affine(z1, W2, b2)
    z2 = relu(u2)
    u3 = affine(z2, W3, b3)
    y  = softmax(u3)
    return y

実行プログラム

既存

import gzip
import numpy as np
# MNIST読み込み
def load_mnist( mnist_path ) :
    return _load_image(mnist_path + 'train-images-idx3-ubyte.gz'), \
           _load_label(mnist_path + 'train-labels-idx1-ubyte.gz'), \
           _load_image(mnist_path + 't10k-images-idx3-ubyte.gz'), \
           _load_label(mnist_path + 't10k-labels-idx1-ubyte.gz')
def _load_image( image_path ) :
    # 画像データの読み込み
    with gzip.open(image_path, 'rb') as f:
        buffer = f.read()
    size = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=4)
    rows = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=8)
    columns = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=12)
    data = np.frombuffer(buffer, np.uint8, offset=16)
    image = np.reshape(data, (size[0], rows[0]*columns[0]))
    image = image.astype(np.float32)
    return image
def _load_label( label_path ) :
    # 正解データ読み込み
    with gzip.open(label_path, 'rb') as f:
        buffer = f.read()
    size = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=4)
    data = np.frombuffer(buffer, np.uint8, offset=8)
    label = np.zeros((size[0], 10))
    for i in range(size[0]):
        label[i, data[i]] = 1
    return label

# 正解率
def accuracy_rate(y, t):
    max_y = np.argmax(y, axis=1)
    max_t = np.argmax(t, axis=1)
    return np.sum(max_y == max_t)/y.shape[0]

正解率、誤差表示

def print_metrics(epoche, x_train, t_train, y_train, x_test, t_test, y_test, Wc, bc, W1, b1, W2, b2, W3, b3):
    # 予測（学習データ）
    if y_train is None:
        y_train = np.zeros_like(t_train)
        for j in range(0, x_train.shape[0], batch_size):
            y_train[j:j+batch_size] = predict(x_train[j:j+batch_size], Wc, bc, W1, b1, W2, b2, W3, b3)
    # 予測（テストデータ）
    if y_test is None:
        y_test = np.zeros_like(t_test)
        for j in range(0, x_test.shape[0], batch_size):
            y_test[j:j+batch_size] = predict(x_test[j:j+batch_size], Wc, bc, W1, b1, W2, b2, W3, b3)
    # 正解率、誤差表示
    train_rate, train_err = accuracy_rate(y_train, t_train), cross_entropy_error(y_train, t_train)
    test_rate, test_err = accuracy_rate(y_test, t_test), cross_entropy_error(y_test, t_test)
    print("{0:3d} train_rate={1:6.2f}% test_rate={2:6.2f}% train_err={3:8.5f} test_err={4:8.5f}".format(epoche, train_rate*100, test_rate*100, train_err, test_err))

CNN対応による見直し

# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('data/')

x_train = x_train.reshape(x_train.shape[0], 1, 28, 28)
x_test  = x_test.reshape(x_test.shape[0], 1, 28, 28)

# 入力データの正規化(0～1)
nx_train = x_train/255
nx_test  = x_test/255

# ノード数設定
un, uc, uh, uw = nx_train.shape
fn, fc, fh, fw = 6, 1, 7, 7 # フィルタサイズ
ps = 2                      # プーリングサイズ
zh, zw = uh-fh+1, uw-fw+1   # 畳み込み後の高さ、幅
zh, zw = int(zh/ps), int(zw/ps) # プーリング後の高さ、幅
d0 = fn * zh * zw
d1 = 100 # 1層目のノード数
d2 = 50  # 2層目のノード数
d3 = 10
# 重みの初期化(-0.1～0.1の乱数)
np.random.seed(8)
Wc = np.random.rand(fn, fc, fh, fw) * 0.2 - 0.1
W1 = np.random.rand(d0, d1) * 0.2 - 0.1
W2 = np.random.rand(d1, d2) * 0.2 - 0.1
W3 = np.random.rand(d2, d3) * 0.2 - 0.1
# バイアスの初期化(0)
bc = np.zeros(fn)
b1 = np.zeros(d1)
b2 = np.zeros(d2)
b3 = np.zeros(d3)

# 学習率
lr = 0.2
# バッチサイズ
batch_size = 100
# 学習回数
epoch = 30

# 誤差、正解率表示
print_metrics(0, nx_train, t_train, None, nx_test, t_test, None, Wc, bc, W1, b1, W2, b2, W3, b3)

for i in range(epoch):
    # データシャッフル
    idx = np.arange(nx_train.shape[0])
    np.random.shuffle(idx)

    # 学習
    y_train = np.zeros_like(t_train)
    for j in range(0, nx_train.shape[0], batch_size):
        y_train[idx[j:j+batch_size]], Wc, bc, W1, b1, W2, b2, W3, b3 = learn(nx_train[idx[j:j+batch_size]], t_train[idx[j:j+batch_size]], Wc, bc, W1, b1, W2, b2, W3, b3, lr)

    # 誤差、正解率表示
    print_metrics(i+1, nx_train, t_train, y_train, nx_test, t_test, None, Wc, bc, W1, b1, W2, b2, W3, b3)

実行結果

30エポック学習するとテストデータの正解率が99%を超えました。

  0 train_rate= 11.37% test_rate= 11.19% train_err= 2.30032 test_err= 2.30044
  1 train_rate= 87.46% test_rate= 97.22% train_err= 0.39273 test_err= 0.09240
  2 train_rate= 97.30% test_rate= 98.19% train_err= 0.08525 test_err= 0.05939
  3 train_rate= 98.17% test_rate= 98.10% train_err= 0.05765 test_err= 0.05944
  4 train_rate= 98.51% test_rate= 98.46% train_err= 0.04546 test_err= 0.05022
  5 train_rate= 98.85% test_rate= 98.56% train_err= 0.03703 test_err= 0.04499
  6 train_rate= 99.06% test_rate= 98.82% train_err= 0.02930 test_err= 0.03938
  7 train_rate= 99.21% test_rate= 98.79% train_err= 0.02379 test_err= 0.04097
  8 train_rate= 99.28% test_rate= 98.61% train_err= 0.02112 test_err= 0.04568
  9 train_rate= 99.42% test_rate= 98.62% train_err= 0.01849 test_err= 0.04329
 10 train_rate= 99.52% test_rate= 98.84% train_err= 0.01562 test_err= 0.03819
 11 train_rate= 99.57% test_rate= 98.87% train_err= 0.01281 test_err= 0.04022
 12 train_rate= 99.67% test_rate= 98.78% train_err= 0.00984 test_err= 0.04401
 13 train_rate= 99.78% test_rate= 98.86% train_err= 0.00739 test_err= 0.04426
 14 train_rate= 99.82% test_rate= 98.94% train_err= 0.00689 test_err= 0.04226
 15 train_rate= 99.89% test_rate= 98.95% train_err= 0.00416 test_err= 0.04169
 16 train_rate= 99.89% test_rate= 98.88% train_err= 0.00424 test_err= 0.04776
 17 train_rate= 99.91% test_rate= 98.88% train_err= 0.00359 test_err= 0.04648
 18 train_rate= 99.94% test_rate= 98.90% train_err= 0.00267 test_err= 0.04460
 19 train_rate= 99.94% test_rate= 98.95% train_err= 0.00196 test_err= 0.04639
 20 train_rate= 99.94% test_rate= 98.94% train_err= 0.00216 test_err= 0.05059
 21 train_rate= 99.98% test_rate= 98.96% train_err= 0.00136 test_err= 0.04540
 22 train_rate= 99.98% test_rate= 98.82% train_err= 0.00090 test_err= 0.05436
 23 train_rate= 99.91% test_rate= 98.80% train_err= 0.00324 test_err= 0.04862
 24 train_rate= 99.95% test_rate= 98.94% train_err= 0.00186 test_err= 0.04695
 25 train_rate= 99.98% test_rate= 98.90% train_err= 0.00102 test_err= 0.04989
 26 train_rate=100.00% test_rate= 98.98% train_err= 0.00043 test_err= 0.04741
 27 train_rate=100.00% test_rate= 99.03% train_err= 0.00024 test_err= 0.04770
 28 train_rate=100.00% test_rate= 99.05% train_err= 0.00018 test_err= 0.04817
 29 train_rate=100.00% test_rate= 99.04% train_err= 0.00017 test_err= 0.04912
 30 train_rate=100.00% test_rate= 99.02% train_err= 0.00014 test_err= 0.04932

私のノートPCでは、約１時間かかりました。通常のニューラルネットワークに比べ非常に時間がかかりました。

結果の表示

学習後のフィルタの表示

学習後にフィルタがどのように変化したか確認してみましょう。
30エポック実行後のフィルタです。

import matplotlib.pyplot as plt

plt.figure(figsize=(16, 2))
for i in range(fn):
    plt.subplot(1, fn, i+1)
    plt.imshow(Wc[i].reshape(fh, fw), 'gray')
    plt.axis('off')
plt.show()

畳み込み、maxプーリング後のデータの表示

実際に畳み込み後に画像がどのように変化しているか確認してみましょう。
テストデータの最初のデータです。このような画像です。

import matplotlib.pyplot as plt

plt.imshow(nx_test[0,0], 'bwr' , vmin = -1, vmax = 1)
plt.axis('off')
plt.show()

畳み込み後、活性化関数後、maxプーリング後にデータがどのように変化したか見てみましょう。正の値を赤、負の値を青で表示しています。

import matplotlib.pyplot as plt

uc = convolution2d(nx_test[0:1], Wc, bc)
zc = relu(uc)
up = max_pooling2d(zc)

for u in [uc, zc, up]:
    print(u.shape)
    plt.figure(figsize=(16, 2))
    for i in range(fn):
        plt.subplot(1, fn, i+1)
        plt.imshow(u[0][i], 'bwr' , vmin = -3, vmax = 3)
        plt.axis('off')
    plt.show()

(1, 6, 22, 22)

(1, 6, 22, 22)

(1, 6, 11, 11)

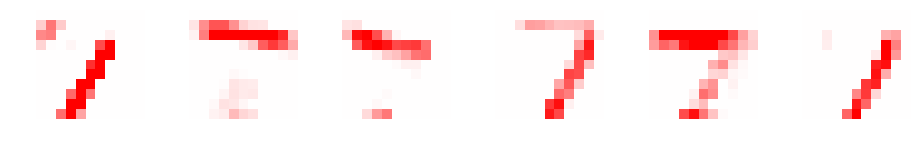
畳み込み後も元の数字のイメージが残っていますね。ReLUは、正の場合のみ通す関数でした。青の部分がなくなっています。maxプーリングは、最大を取っているのでより強調したイメージになっています。
こうやって表示してみると面白いですね。

CNNに対応することで、MNISTのテストデータの正解率が、99%を超えました。
本来であれば、畳み込みには、パディングやストライドの指定やmaxプーリングには、プールサイズも指定もありますが、実装を単純化するため省いております。「ディープラーニングを実装から学ぶ（9-1）CNNの実装」では、それらにも対応しているので興味がある方は、参照してみてください。