numpyの行列演算の可否が良く分からなくなるためまとめます。
ここでは、2次元までの配列および四則演算を考えます。
numpyを利用しますので、事前にnumpyをインポートします。
import numpy as np
行列
1次元
1次元で要素数3の行列を考えます。
X3 =
\begin{pmatrix}
x_1 & x_2 & x_3
\end{pmatrix}
numpyにて1次元で要素数3の行列を定義し、shapeにて次元、要素数を確認します。
X3 = np.array([1,2,3])
print("X3 = ")
print(X3)
print("X3.shape = " + str(X3.shape))
X3 =
[1 2 3]
X3.shape = (3,)
1次元の場合、列方向(横方向)になります。
ここでは、(3)行列と表します。
2次元
2次元で要素数2×3の行列を考えます。
X23 =
\begin{pmatrix}
x_{11} & x_{12} & x_{13}\\
x_{21} & x_{22} & x_{23}
\end{pmatrix}
numpyにて2次元で要素数2×3の行列を定義し、shapeにて次元、要素数を確認します。
X23 = np.array([[1,2,3],[4,5,6]])
print("X23 = ")
print(X23)
print("X23.shape = " + str(X23.shape))
X23 =
[[1 2 3]
[4 5 6]]
X23.shape = (2, 3)
2次元の場合、**1次元目が行方向(縦方向)、2次元目が列方向(横方向)**になります。
1次元の場合から(3, 2)となりそうですが、逆になるので注意が必要です。
ここでは、(2,3)行列と表します。
1次元(行方向)
行方向の1次元配列は、2次元で表します。
X31 =
\begin{pmatrix}
x_{11}\\
x_{21}\\
x_{31}
\end{pmatrix}
X31 = np.array([[1],[2],[3]])
print("X31 = ")
print(X31)
print("X31.shape = " + str(X31.shape))
X31 =
[[1]
[2]
[3]]
X31.shape = (3, 1)
ここでは、(3,1)行列と表します。
スカラー関連
スカラーとの演算は、行列の各要素との演算になります。
a +
\begin{pmatrix}
x_{11} & x_{12} & x_{13}\\
x_{21} & x_{22} & x_{23}
\end{pmatrix}
=
\begin{pmatrix}
a+x_{11} & a+x_{12} & a+x_{13}\\
a+x_{21} & a+x_{22} & a+x_{23}
\end{pmatrix}
\\
\begin{pmatrix}
x_{11} & x_{12} & x_{13}\\
x_{21} & x_{22} & x_{23}
\end{pmatrix}
+ a =
\begin{pmatrix}
x_{11}+a & x_{12}+a & x_{13}+a\\
x_{21}+a & x_{22}+a & x_{23}+a
\end{pmatrix}
スカラー
先ほどのX23に2を足した結果です。
a = 2
print("a + X23 = ")
print(a + X23)
print("X23 + a = ")
print(X23 + a)
a + X23 =
[[3 4 5]
[6 7 8]]
X23 + a =
[[3 4 5]
[6 7 8]]
足し算の例を示しましたが、加減乗除とも同じです。以降、足し算の例を示しますが加減乗除とも同じ結果になります。引き算、割り算は順序がありますので注意してください。
(1)行列
(1)行列はスカラーと同じです。
X1 = np.array([2])
print("X1 = ")
print(X1)
print("X1.shape = " + str(X1.shape))
print("X1 + X23 = ")
print(X1 + X23)
print("X23 + X1 = ")
print(X23 + X1)
X1 =
[2]
X1.shape = (1,)
X1 + X23 =
[[3 4 5]
[6 7 8]]
X23 + X1 =
[[3 4 5]
[6 7 8]]
(1,1)行列
(1,1)行列もスカラーと同じです。
X11 = np.array([[2]])
print("X11 = ")
print(X11)
print("X11.shape = " + str(X11.shape))
print("X11 + X23 = ")
print(X11 + X23)
print("X23 + X11 = ")
print(X23 + X11)
X11 =
[[2]]
X11.shape = (1, 1)
X11 + X23 =
[[3 4 5]
[6 7 8]]
X23 + X11 =
[[3 4 5]
[6 7 8]]
1次元
1次元 + 1次元
1次元の行列と演算可能な1次元の行列は同じ要素数の行列のみです。
\begin{pmatrix}
x_1 & x_2 & x_3
\end{pmatrix}
+
\begin{pmatrix}
y_1 & y_2 & y_3
\end{pmatrix}
=
\begin{pmatrix}
x_1+y_1 & x_2+y_2 & x_3+y_3
\end{pmatrix}
実行します。
print("X3 = ")
print(X3)
Y3 = np.array([2,4,6])
print("Y3 = ")
print(Y3)
print("Y3.shape = " + str(Y3.shape))
print("X3 + Y3 = ")
print(X3 + Y3)
X3 =
[1 2 3]
Y3 =
[2 4 6]
Y3.shape = (3,)
X3 + Y3 =
[3 6 9]
要素数が2の場合はエラーとなります。
print("X3 = ")
print(X3)
Y2 = np.array([2,4])
print("Y2 = ")
print(Y2)
print("Y2.shape = " + str(Y2.shape))
print("X3 + Y2 = ")
print(X3 + Y2)
以下のエラーとなります。
ValueError: operands could not be broadcast together with shapes (3,) (2,)
1次元 + 2次元
1行
1行で要素数の同じ行列であれば演算が可能です。
\begin{pmatrix}
x_1 & x_2 & x_3
\end{pmatrix}
+
\begin{pmatrix}
y_{11} & y_{12} & y_{13}
\end{pmatrix}
=
\begin{pmatrix}
x_1+y_{11} & x_2+y_{12} & x_3+y_{13}
\end{pmatrix}
print("X3 = ")
print(X3)
Y13 = np.array([[2,4,6]])
print("Y13 = ")
print(Y13)
print("Y13.shape = " + str(Y13.shape))
print("X3 + Y13 = ")
print(X3 + Y13)
X3 =
[1 2 3]
Y13 =
[[2 4 6]]
Y13.shape = (1, 3)
X3 + Y13 =
[[3 6 9]]
1列
1列の行列であれば演算が可能です。例では、4行ですが、(n,1)行列であれば演算可能です。
\begin{pmatrix}
x_1 & x_2 & x_3
\end{pmatrix}
+
\begin{pmatrix}
y_{11}\\
y_{21}\\
y_{31}\\
y_{41}
\end{pmatrix}
=
\begin{pmatrix}
x_1+y_{11} & x_2+y_{11} & x_3+y_{11}\\
x_1+y_{21} & x_2+y_{21} & x_3+y_{21}\\
x_1+y_{31} & x_2+y_{31} & x_3+y_{31}\\
x_1+y_{41} & x_2+y_{41} & x_3+y_{41}
\end{pmatrix}
print("X3 = ")
print(X3)
Y41 = np.array([[2],[4],[6],[8]])
print("Y41 = ")
print(Y41)
print("Y41.shape = " + str(Y41.shape))
print("X3 + Y41 = ")
print(X3 + Y41)
X3 =
[1 2 3]
Y41 =
[[2]
[4]
[6]
[8]]
Y41.shape = (4, 1)
X3 + Y41 =
[[ 3 4 5]
[ 5 6 7]
[ 7 8 9]
[ 9 10 11]]
同一列数
列数が同じ場合に演算が可能です。(2,3)行列の例を示しますが、(n,3)行列との演算が可能です。
各行ごとに演算が実行されます。
\begin{pmatrix}
x_1 & x_2 & x_3
\end{pmatrix}
+
\begin{pmatrix}
y_{11} & y_{12} & y_{13}\\
y_{21} & y_{22} & y_{23}
\end{pmatrix}
=
\begin{pmatrix}
x_1+y_{11} & x_2+y_{12} & x_3+y_{13}\\
x_1+y_{21} & x_2+y_{22} & x_3+y_{23}
\end{pmatrix}
print("X3 = ")
print(X3)
Y23 = np.array([[2,4,6],[8,10,12]])
print("Y23 = ")
print(Y23)
print("Y23.shape = " + str(Y23.shape))
print("X3 + Y23 = ")
print(X3 + Y23)
X3 =
[1 2 3]
Y23 =
[[ 2 4 6]
[ 8 10 12]]
Y23.shape = (2, 3)
X3 + Y23 =
[[ 3 6 9]
[ 9 12 15]]
列数が異なる場合、例えば、(2,2)行列の場合は、エラーとなります。
ValueError: operands could not be broadcast together with shapes (3,) (2,2)
2次元
2次元+1次元
2次元の行列と演算可能な1次元の行列は列数が同じ行列のみです。
\begin{pmatrix}
x_{11} & x_{12} & x_{13}\\
x_{21} & x_{22} & x_{23}
\end{pmatrix}
+
\begin{pmatrix}
y_1 & y_2 & y_3
\end{pmatrix}
=
\begin{pmatrix}
x_{11}+y_1 & x_{12}+y_2 & x_{13}+y_3\\
x_{21}+y_1 & x_{22}+y_2 & x_{23}+y_3
\end{pmatrix}
print("X23 = ")
print(X23)
Y3 = np.array([2,4,6])
print("Y3 = ")
print(Y3)
print("Y3.shape = " + str(Y3.shape))
print("X23 + Y3 = ")
print(X23 + Y3)
X23 =
[[1 2 3]
[4 5 6]]
Y3 =
[2 4 6]
Y3.shape = (3,)
X23 + Y3 =
[[ 3 6 9]
[ 6 9 12]]
2次元+2次元
同一列数1行
1行で列数が同一の行列と演算が可能です。
\begin{pmatrix}
x_{11} & x_{12} & x_{13}\\
x_{21} & x_{22} & x_{23}
\end{pmatrix}
+
\begin{pmatrix}
y_{11} & y_{12} & y_{13}
\end{pmatrix}
=
\begin{pmatrix}
x_{11}+y_{11} & x_{12}+y_{12} & x_{13}+y_{13}\\
x_{21}+y_{11} & x_{22}+y_{12} & x_{23}+y_{13}
\end{pmatrix}
print("X23 = ")
print(X23)
Y13 = np.array([[2,4,6]])
print("Y13 = ")
print(Y13)
print("Y13.shape = " + str(Y13.shape))
print("X23 + Y13 = ")
print(X23 + Y13)
X23 =
[[1 2 3]
[4 5 6]]
Y13 =
[[2 4 6]]
Y13.shape = (1, 3)
X23 + Y13 =
[[ 3 6 9]
[ 6 9 12]]
同一行数1列
1列で行数が同一の行列と演算が可能です。
\begin{pmatrix}
x_{11} & x_{12} & x_{13}\\
x_{21} & x_{22} & x_{23}
\end{pmatrix}
+
\begin{pmatrix}
y_{11}\\
y_{21}
\end{pmatrix}
=
\begin{pmatrix}
x_{11}+y_{11} & x_{12}+y_{11} & x_{13}+y_{11}\\
x_{21}+y_{21} & x_{22}+y_{21} & x_{23}+y_{21}
\end{pmatrix}
print("X23 = ")
print(X23)
Y21 = np.array([[2],[4]])
print("Y21 = ")
print(Y21)
print("Y21.shape = " + str(Y21.shape))
print("X23 + Y21 = ")
print(X23 + Y21)
X23 =
[[1 2 3]
[4 5 6]]
Y21 =
[[2]
[4]]
Y21.shape = (2, 1)
X23 + Y21 =
[[ 3 4 5]
[ 8 9 10]]
同一行列数
行、列とも同一の行列と演算が可能です。
\begin{pmatrix}
x_{11} & x_{12} & x_{13}\\
x_{21} & x_{22} & x_{23}
\end{pmatrix}
+
\begin{pmatrix}
y_{11} & y_{12} & y_{13}\\
y_{21} & y_{22} & y_{23}
\end{pmatrix}
=
\begin{pmatrix}
x_{11}+y_{11} & x_{12}+y_{12} & x_{13}+y_{13}\\
x_{21}+y_{21} & x_{22}+y_{22} & x_{23}+y_{23}
\end{pmatrix}
print("X23 = ")
print(X23)
Y23 = np.array([[2,4,6],[8,10,12]])
print("Y23 = ")
print(Y23)
print("Y23.shape = " + str(Y23.shape))
print("X23 + Y23 = ")
print(X23 + Y23)
X23 =
[[1 2 3]
[4 5 6]]
Y23 =
[[ 2 4 6]
[ 8 10 12]]
Y23.shape = (2, 3)
X23 + Y23 =
[[ 3 6 9]
[12 15 18]]
まとめ
スカラー
スカラーは、すべての行列との演算が可能。各要素ごとにスカラーと演算した結果となる。
1次元
(m)行列と演算可能な行列は、以下の通り。
- (m)行列:要素数が同じ
- (1,m)行列:列数が同じで行数が1
- (n,1)行列:列数が1。nは任意
- (n,m)行列:列数が同じ。nは任意
2次元
(n,m)行列と演算可能な行列は、以下の通り。
- (m)行列:列数が同じ
- (1,m)行列:列数が同じで行数が1
- (n,1)行列:行数が同じで列数が1
- (n,m)行列:行数、列数とも同じ
整理すると、行数または列数が同じで、行数または列数の異なる方は1であること。
ただし、1次元の行列では、1次元目が列になることに注意が必要
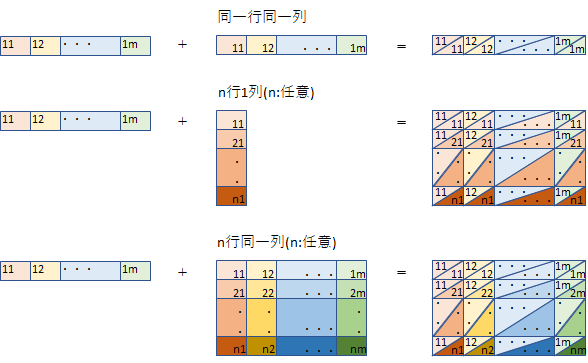
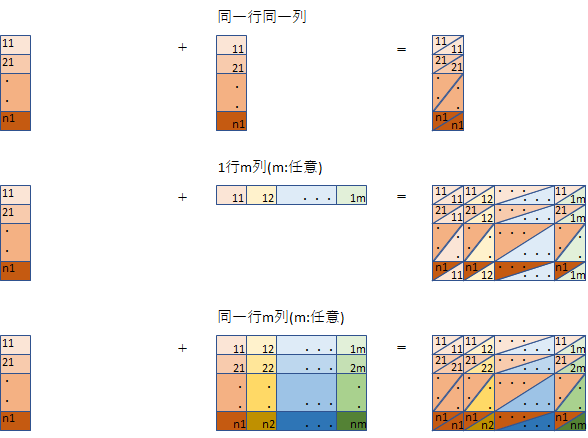
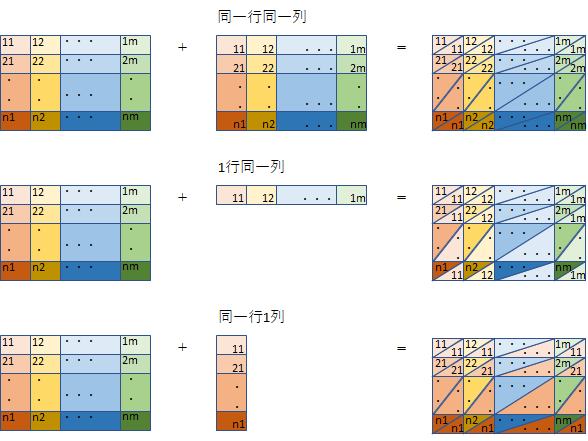
図
記号だと分かりにくいので図にしてみます。どの要素ごとに演算されるか明確となるように色付けしましたが逆に分かりにくくなりました。形を見てください。形から演算可能か判断できます。スカラーとの演算は省略しています。
(m)行列、(1,m)行列
(n,1)行列
(n,m)行列
図にするとイメージがわきますね。
次回、軸についてまとめたいと考えています。演算の可否、特に1次元の場合が重要になりますので、覚えておいてください。